基于模型預(yù)測(cè)控制的無(wú)人駕駛汽車的軌跡跟蹤*

李金良 郝亮 曹植

（遼寧工業(yè)大學(xué)）

隨著計(jì)算機(jī)信息處理技術(shù)、傳感器技術(shù)和汽車控制技術(shù)的進(jìn)步，基于高效環(huán)境感知的輔助駕駛技術(shù)或全自動(dòng)駕駛技術(shù)迅速發(fā)展，以主動(dòng)控制為核心的先進(jìn)汽車安全技術(shù)必將是現(xiàn)代交通系統(tǒng)和未來(lái)高度智能化交通系統(tǒng)的核心技術(shù)之一[1-2]。實(shí)現(xiàn)對(duì)全自主無(wú)人駕駛汽車在高速和冰雪等復(fù)雜路面安全穩(wěn)定的軌跡跟蹤控制具有十分重要的意義。由于線性時(shí)變模型預(yù)測(cè)控制算法相比于非線性模型預(yù)測(cè)控制算法具有計(jì)算簡(jiǎn)單和實(shí)時(shí)性好等優(yōu)點(diǎn)[3]，因此，文章通過(guò)MATLAB/Simulink軟件搭建基于運(yùn)動(dòng)學(xué)模型的線性時(shí)變模型預(yù)測(cè)控制算法，研究在給定工況下的軌跡跟蹤特性。

1 線性時(shí)變模型預(yù)測(cè)控制原理

以線性狀態(tài)控制模型為基礎(chǔ)，依次推導(dǎo)模型預(yù)測(cè)控制的預(yù)測(cè)方程、優(yōu)化求解及反饋機(jī)制[4]。

1.1 預(yù)測(cè)方程

首先考慮離散線性化模型：

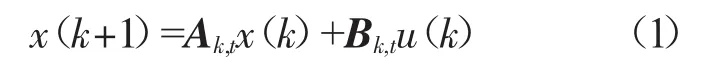
式中：x（k）——n維狀態(tài)變量；

u（k）——m維控制輸入變量；

Ak,t——狀態(tài)變量系數(shù)矩陣；

Bk,t——控制變量系數(shù)矩陣。

為了使整個(gè)離散化模型的關(guān)系更加明確，將系統(tǒng)未來(lái)時(shí)刻的輸出以矩陣的形式表達(dá)：

式中：η（t）——預(yù)測(cè)時(shí)域Np內(nèi)的變形后系統(tǒng)輸出變量；

ξ（t）——預(yù)測(cè)時(shí)域Np內(nèi)的變形后系統(tǒng)狀態(tài)變量；

Ct——輸出系數(shù)矩陣；

ΔU（t）——控制時(shí)域Nc內(nèi)的系統(tǒng)輸入增量；

ψt——變形后的系統(tǒng)輸入變量狀態(tài)矩陣；

θt——變形后的系統(tǒng)輸入增量狀態(tài)矩陣。

通過(guò)觀察式（2），可以看到，在預(yù)測(cè)時(shí)域內(nèi)的狀態(tài)量和輸出量都可以通過(guò)系統(tǒng)當(dāng)前的狀態(tài)量（ξ（t｜t））和控制時(shí)域內(nèi)的控制增量（ΔU（t））計(jì)算得到。這也就是模型預(yù)測(cè)控制算法中“預(yù)測(cè)”功能的實(shí)現(xiàn)。

1.2 QP（二次規(guī)劃）問(wèn)題的轉(zhuǎn)化

系統(tǒng)控制時(shí)域（Nc）內(nèi)的 ΔU（t）是未知的，通過(guò)設(shè)定合理的優(yōu)化目標(biāo)函數(shù)并使其最小化，可求得在Nc內(nèi)滿足約束條件的最優(yōu)控制序列。

考慮目標(biāo)函數(shù)如下：

式中：η（t+i｜t）——參考輸出量，i=1,…,Np；

ηref（t+i｜t）——理想?yún)⒖驾敵隽浚琲=1,…,Np；

Δu（t+i｜t）——輸入增量，i=1,…,Nc-1；

Q，R——權(quán)重矩陣。

其中，第1項(xiàng)（Q的2范數(shù)）用于懲罰系統(tǒng)在Np內(nèi)，輸出量與參考輸出量之間的偏差，即反映了系統(tǒng)對(duì)參考軌跡的快速跟蹤能力；第2項(xiàng)（R的2范數(shù)）用于懲罰系統(tǒng)在Nc內(nèi)的控制增量大小，即反映了系統(tǒng)對(duì)控制量平穩(wěn)變化的要求；同時(shí)，在實(shí)際的控制系統(tǒng)中，往往需要滿足系統(tǒng)狀態(tài)量及控制量的一些約束條件，一般如下：

控制量約束：

控制增量約束：

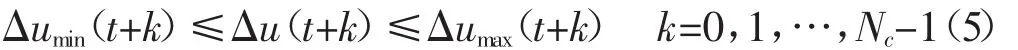
輸出約束：

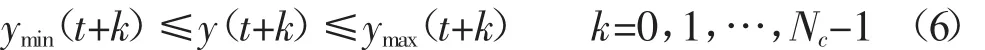
1.3 反饋控制

在每個(gè)控制周期內(nèi)完成對(duì)式（5）求解后，得到了控制時(shí)域內(nèi)的一系列控制輸入增量：

根據(jù)模型預(yù)測(cè)控制的基本原理，將該控制序列中第1個(gè)元素作為實(shí)際的控制輸入增量作用于系統(tǒng)，即：

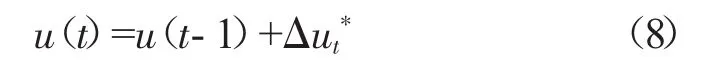
式中：u（t）——系統(tǒng)的實(shí)際控制量。

系統(tǒng)執(zhí)行這一控制量直到下一時(shí)刻。在新的時(shí)刻，系統(tǒng)根據(jù)狀態(tài)信息重新預(yù)測(cè)下一階段時(shí)域的輸出，通過(guò)優(yōu)化過(guò)程得到一個(gè)新的控制增量序列。如此循環(huán)往復(fù)，直至系統(tǒng)完成控制過(guò)程。

2 線性時(shí)變模型預(yù)測(cè)控制仿真

2.1MATLAB仿真條件

無(wú)人駕駛汽車從坐標(biāo)原點(diǎn)出發(fā)，以期望縱向速度（v=1m/s）跟蹤一條直線軌跡（y=3m），采樣時(shí)間為50ms，仿真總時(shí)間設(shè)定為20 s。

2.2 低速運(yùn)動(dòng)學(xué)模型線性化處理

由于控制目標(biāo)是無(wú)人駕駛汽車在低速情況下的跟蹤控制，因此考慮以汽車運(yùn)動(dòng)學(xué)方程作為預(yù)測(cè)模型，低速情況下的汽車運(yùn)動(dòng)學(xué)方程形式如下[5]：

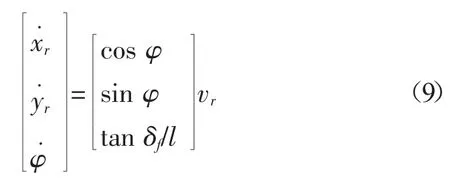
式中：xr，yr——汽車后軸軸心處的橫縱坐標(biāo)；

φ——汽車航向角，（°）；

δf——前輪轉(zhuǎn)角，（°）；

l——汽車軸距，m；

vr——汽車后軸中心的速度，m/s。

對(duì)其進(jìn)行線性化，得到線性時(shí)變模型為：

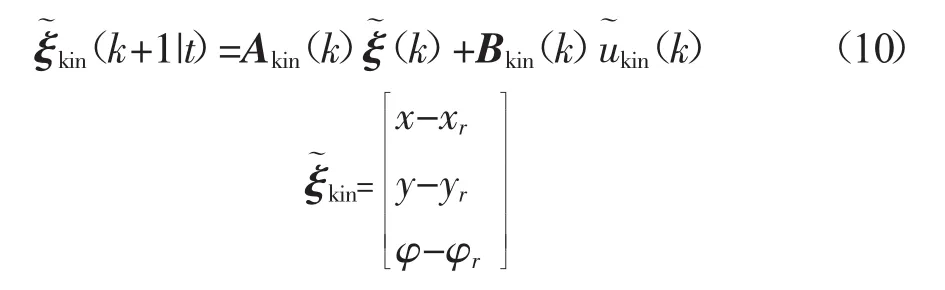
式中：T——采樣時(shí)間，s；

δf,r——汽車在r點(diǎn)的前輪轉(zhuǎn)角，（°）。

2.3 汽車運(yùn)動(dòng)學(xué)模型的驗(yàn)證

為驗(yàn)證所建立的汽車運(yùn)動(dòng)學(xué)模型，在MATLAB/Simulink環(huán)境中搭建該運(yùn)動(dòng)學(xué)模型，對(duì)無(wú)人駕駛汽車的直線軌跡跟蹤過(guò)程進(jìn)行仿真驗(yàn)證，其仿真結(jié)果，如圖1～圖4所示。

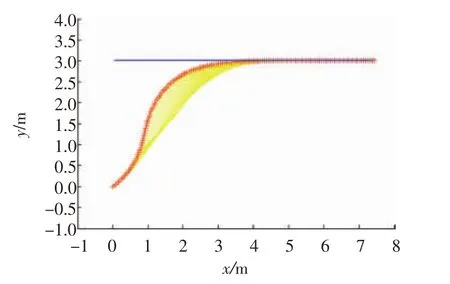
圖1 跟蹤理想軌跡的實(shí)際運(yùn)行結(jié)果

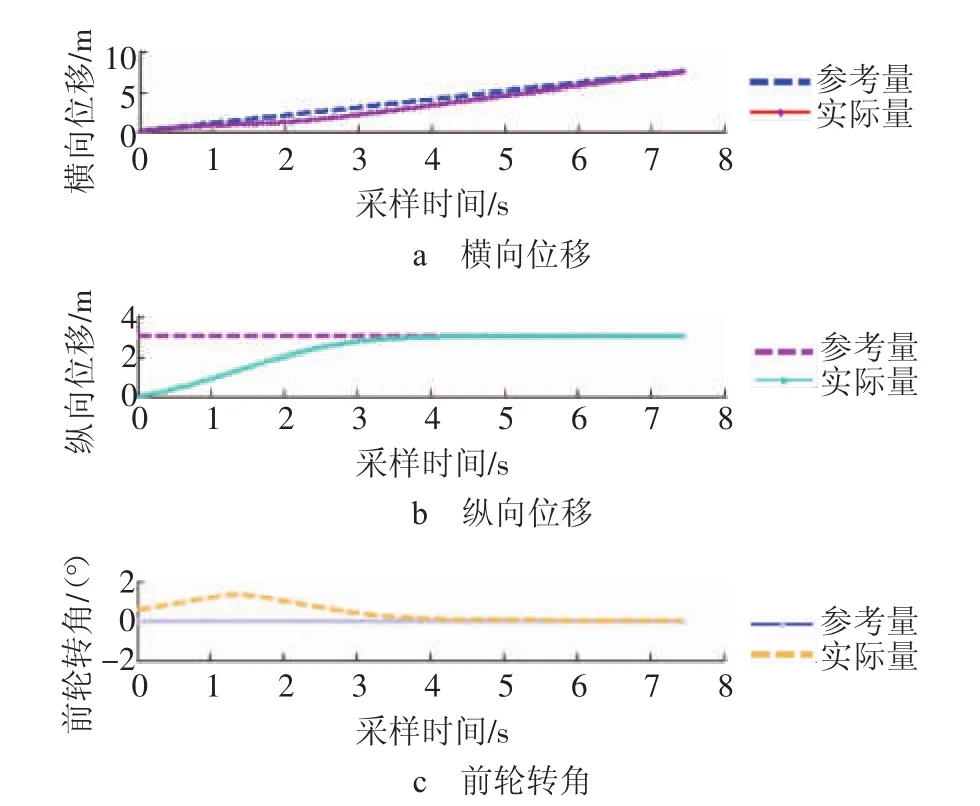
圖2 系統(tǒng)狀態(tài)量隨時(shí)間的變化曲線

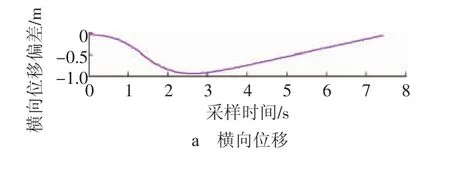
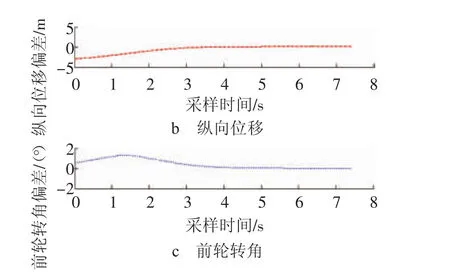
圖3 狀態(tài)量偏差隨時(shí)間的變化曲線

圖4 控制量隨時(shí)間的變化曲線

由圖1可以看出，實(shí)際軌跡從原點(diǎn)出發(fā)能夠跟蹤上真實(shí)直線軌跡（y=3 m）；由圖2和圖3可知，汽車的橫向、縱向位移和前輪轉(zhuǎn)角均能很好地跟蹤理想軌跡，最終達(dá)到穩(wěn)定狀態(tài)；由圖4可知，無(wú)人駕駛的控制量縱向速度和角加速度均能最終達(dá)到穩(wěn)定的狀態(tài)。

3 結(jié)論

文章通過(guò)線性時(shí)變模型預(yù)測(cè)控制仿真得出，無(wú)人駕駛的狀態(tài)量和控制量均能很好地反映出汽車在跟蹤過(guò)程中，實(shí)際狀態(tài)量均能實(shí)時(shí)跟蹤理想的狀態(tài)量實(shí)時(shí)狀態(tài)變化，最終達(dá)到穩(wěn)定狀態(tài)，控制量也經(jīng)過(guò)一定變化達(dá)到最終的穩(wěn)定狀態(tài)，這說(shuō)明在低速跟蹤過(guò)程中，線性時(shí)變模型預(yù)測(cè)控制算法能夠?qū)崟r(shí)跟蹤汽車的行駛軌跡，并且保證汽車行駛過(guò)程中的實(shí)時(shí)性和穩(wěn)定性。