葡萄酒的評價模型

繆子陽，李婷玉，祝夢琳

（1.南京郵電大學(xué)管理學(xué)院，江蘇南京210000；2.南京郵電大學(xué)貝爾英才學(xué)院，江蘇南京210000）

葡萄酒的評價模型

繆子陽1，李婷玉2，祝夢琳1

（1.南京郵電大學(xué)管理學(xué)院，江蘇南京210000；2.南京郵電大學(xué)貝爾英才學(xué)院，江蘇南京210000）

對于多個葡萄酒樣品，2組評酒員的打分不盡相同。要解決的就是通過顯著性檢驗來判別不同組別的評酒員的打分是否具有顯著性差異，同時根據(jù)2組評分的方差的平均值來判斷哪一組的可信度更高；對釀酒葡萄進行聚類分析。

葡萄酒；t-檢驗；聚類分析；多元線性回歸

葡萄酒質(zhì)量的好壞通常都是聘請一些專業(yè)的評酒員來鑒定。而葡萄酒的質(zhì)量往往與釀酒葡萄有關(guān)，因此對釀酒葡萄的理化指標、葡萄酒本身的理化指標和葡萄酒質(zhì)量這三者的關(guān)系進行研究是十分必要的[1]。本文結(jié)合2012年全國大學(xué)生數(shù)學(xué)建模競賽A題建立數(shù)學(xué)模型對葡萄酒進行評價。

1 問題分析

對于問題一，分析2組評酒員的評價結(jié)果有無顯著性差異，將紅、白2種葡萄酒分別進行顯著性檢驗。首先將每位評酒員對每種樣品葡萄酒的各指標評分進行求和，得到總評分，然后對每一種葡萄酒樣品的2組的10個總評分進行t-檢驗，最后總體分析對于紅、白2種葡萄酒，不同組別的評酒員的評分是否具有顯著性差異。此過程可以通過SPSS軟件進行數(shù)據(jù)分析得出結(jié)果。

對于問題一中分析哪一組的評價結(jié)果更可信，首先計算出2個組的10個評酒員對每一樣品葡萄酒的總評分的方差，再分別計算2個組對紅、白2種葡萄酒不同樣品總評分的方差的平均值，求得的平均值越小，說明評價值越穩(wěn)定，可信度越高。法二對2個組對紅、白葡萄酒評分的平均差進行比較，較小者可信度高。

對于問題二，將釀酒葡萄進行聚類分析，可以以第一問比較可信的那組的葡萄酒質(zhì)量評分和釀酒葡萄的理化指標為依據(jù)。對于葡萄酒的質(zhì)量，采用問題一求解出的可信度較高的一組總評分來衡量，將釀酒葡萄的理化指標無量綱化，利用MATLAB軟件進行聚類分析，可分別對紅、白2種葡萄酒進行分級。

2 基本模型假設(shè)

假設(shè)各評酒員的評價水平穩(wěn)定，不發(fā)生改變；各評酒員之間的評價結(jié)果相互獨立，互不影響。

3 基本符號說明

X1ij表示第1組各評酒員對各紅葡萄酒樣品的總評分（i表示評酒員編號，j表示酒樣品編號，下同），x2ij表示第2組各評酒員對各紅葡萄酒樣品的總評分，x3ij表示第1組各評酒員對各白葡萄酒樣品的總評分，x4ij表示第2組各評酒員對各白葡萄酒樣品的總評分。

4 模型的建立與求解

4.1 對問題一的求解

4.1.1 模型的建立

4.1.1.1 顯著性檢驗

分析2組評酒員的評價結(jié)果有無顯著性差異，將紅、白2種葡萄酒分別進行顯著性檢驗。首先將每位評酒員對每種樣品葡萄酒的各指標評分進行求和，得到總評分，然后對每一種葡萄酒樣品的2組的10個總評分進行t-檢驗，最后總體分析對于紅、白2種葡萄酒，不同組別的評酒員的打分是否具有顯著性差異。

首先對紅葡萄酒的2組評分樣中的每一種葡萄酒樣品進行方差的齊性檢驗，此題運用Levene方差齊性檢驗?zāi)Ｐ蚚2]，進行F-檢驗。檢驗假設(shè)H0∶σ1＝σ2＝…＝σk，即各處理組方差相等；H1∶σi≠σj，即各處理組方差不全相等。取α＝0.01或α＝0.05.計算檢驗統(tǒng)計量F值：

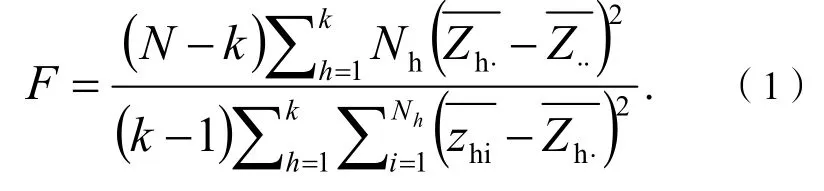
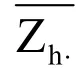
Zhi的定義公式如下：

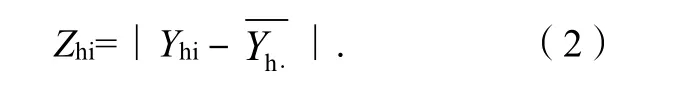
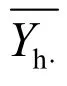
然后對紅葡萄酒的2組評分樣中的每一種葡萄酒樣品進行樣本平均數(shù)差異的顯著性檢驗。運用SPSS軟件處理數(shù)據(jù)，進行數(shù)據(jù)等同性t-檢驗[3]。

檢驗假設(shè)H0∶μ1＝μ2；H1∶μi≠μ2，即各處理組方差不全相等。取α＝0.01或α＝0.05.

構(gòu)造檢驗統(tǒng)計量t并計算：

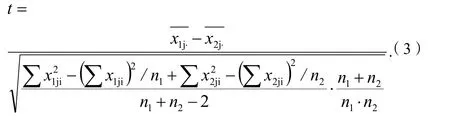
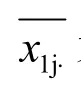
4.1.1.2 可信度評價

對于分析哪一組的評價結(jié)果更可信，法一首先計算出2個組的10個評酒員對每一樣品葡萄酒的總評分的方差，再分別計算2個組對紅、白2種葡萄酒不同樣品總評分的方差的平均值，求得的平均值越小，說明評價值越穩(wěn)定，可信度越高。法二對2個組對紅、白葡萄酒評分的平均差進行比較，較小者可信度高。

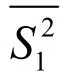
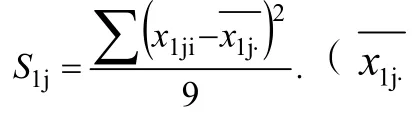
運用平均差評價時，對每種酒樣品的10個總評分計算平均差，再計算每組評價的平均平均差。

對于第1組紅葡萄酒的評分，每種酒樣品的平均差為：

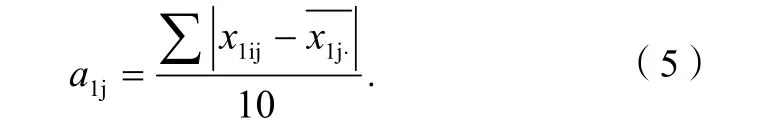
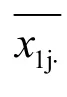
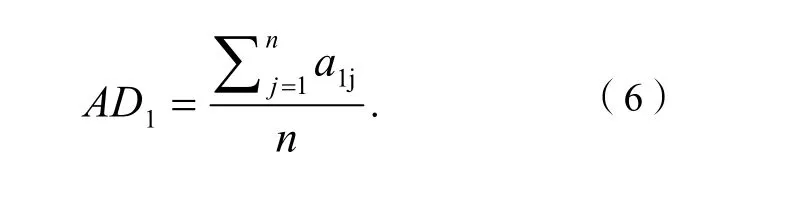
第1組評分的平均差：式（6）中：n為樣品數(shù)目。

同理對于第2組，對紅葡萄酒的評分以及白葡萄酒的2組評分也作上述處理，此處不再贅述。

4.1.2 模型的求解

4.1.2.1 顯著性評價結(jié)果

對于顯著性檢驗，運用SPSS軟件處理數(shù)據(jù)，得到紅、白2種葡萄酒的每一種樣品的2組總評分的顯著性檢驗結(jié)果，紅葡萄酒的27組評價結(jié)果中，在0.05顯著水平上，有樣品2，3，11，12，13，16，23，24這8個樣品的2組評價結(jié)果有顯著性差異；在0.01顯著水平上，只有12，23這2組存在顯著性差異。所以可以認為，對于紅葡萄酒，2組評分結(jié)果不存在顯著性差異。同理，白葡萄酒的28組評價結(jié)果中，在0.05顯著水平上，有樣品5，27這2組存在顯著性差異；在0.01顯著水平上，沒有存在顯著性差異的組。所以認為，對于白葡萄酒，2組評分結(jié)果不存在顯著性差異。

綜上，對于紅、白2種葡萄酒，2組的評分結(jié)果都不存在顯著性差異。

4.1.2.2 可信度評價結(jié)果

對于分析哪組評價結(jié)果可信度高，根據(jù)模型可以求得一系列方差數(shù)據(jù)，得到不管是紅葡萄酒的評分，還是白葡萄酒，都是第2組給出的評分穩(wěn)定，即紅、白2種葡萄酒的評分都是第2組的可信度高。

運用平均差評價的方法，也可以得到一系列平均差值及最終的平均平均差，AD1＝6.48，AD2＝4.71，AD3＝9.05，AD4＝5.85，顯然AD1＞AD2，AD3＞AD4.因此可以認為不管是紅葡萄酒的評分，還是白葡萄酒，都是第2組給出的評分穩(wěn)定，也即紅、白2種葡萄酒的評分都是第2組的可信度高。

綜合2種可信度評價的方法，可以得到相同的結(jié)果，即不管是紅葡萄酒的評分，還是白葡萄酒，都是第2組給出的評分穩(wěn)定，也即紅、白2種葡萄酒的評分都是第2組的可信度高。運用2種方法求出的結(jié)果相同，也說明模型的可靠性。

4.2 對問題二的求解

4.2.1 模型的建立

設(shè)Yi＝（Yi1，Yi2，Yi3，…，Yi30，Yi31）表示第i個酒釀葡萄樣品的理化指標和葡萄酒的質(zhì)量為（Yi1，Yi2，Yi3，…，Yi30，Yi31）個指標統(tǒng)計值的樣本均值為μj，樣本方差為σ.

根據(jù)釀酒葡萄的理化指標和葡萄酒的質(zhì)量對這些釀酒葡萄進行分級，對于葡萄酒的質(zhì)量，采用問題一求解出的可信度較高的一組（組二）的總評分來衡量，即：

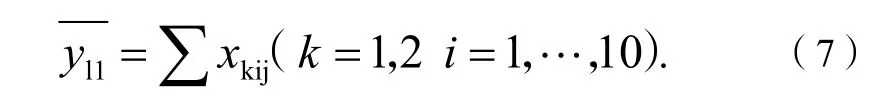
酒釀葡萄的理化指標采用了附件2中所給的30個一級指標，對于其中有多次測量的指標，取平均值。

由于各指標量綱不統(tǒng)一，且數(shù)據(jù)相差懸殊，為了消除不同量級和不同量綱指標對距離的影響，先將樣本數(shù)據(jù)進行標準化處理，采用Zscore法進行如下變換：

設(shè)dij表示第i個酒釀葡萄樣品的理化指標和葡萄酒的質(zhì)量Yi與第k個酒釀葡萄樣品的理化指標和葡萄酒的質(zhì)量Yk之間的歐式標準距離，即：

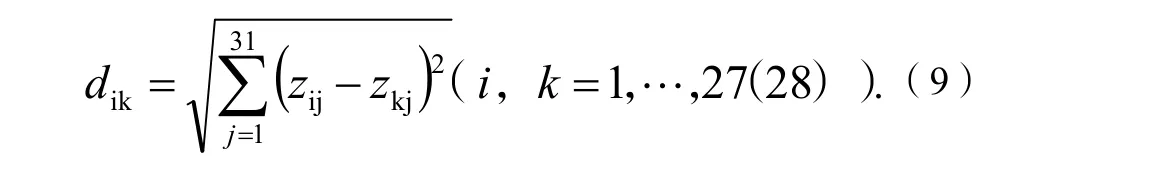
dij越小，表示第i個酒釀葡萄樣品的理化指標和葡萄酒的質(zhì)量與第j個酒釀葡萄樣品的理化指標和葡萄酒的質(zhì)量整體情況越接近，即這2個葡萄樣品劃為一類的機會就越大。

4.2.2 模型的求解

利用MATLAB軟件進行聚類分析，可分別對紅、白2種葡萄酒的酒釀葡萄進行分類，得到譜系圖。根據(jù)譜系圖，將紅葡萄酒酒釀葡萄分為5類，分類結(jié)果為{11}，{1}，{10}，{3}，{2，4，5，6，7，8，9，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27}。將白葡萄酒分為7類，分類結(jié)果為{27}，{3}，{15}，{1，13}，{22}，{8，11，16}，{2，4，5，6，7，9，10，12，14，17，18，19，20，21，23，24，25，26，28}。

再通過計算每一類酒釀葡萄對應(yīng)的葡萄酒的評分的平均值，按照評分的高低排序，對其進行分級。

5 總結(jié)

經(jīng)總結(jié)，得出以下結(jié)論：①問題一中分析2組評分的可信度運用方差和平均差2種方法分析，且得到相同的結(jié)果，驗證了模型的正確性與可靠性；②對數(shù)據(jù)進行歸一化處理，消除量剛不同的問題；③不僅分析出理化指標間的關(guān)聯(lián)度，還運用多元線性回歸給出具體的表達式；④葡萄分級的結(jié)果存在明顯的極端現(xiàn)象，有些級別分到的樣品過少，而有些級別過多，需要運用其他模型，比如模糊綜合評價等方法進行改進。

［1］劉偉城.葡萄酒的評價［J］.才智，2013（10）：312.

［2］程琮，范華.Levene方差齊性檢驗［J］.中國衛(wèi)生統(tǒng)計，2005，22（6）：408-409.

［3］孫立宏.獨立樣本平均數(shù)差異的顯著性檢驗方法與應(yīng)用［J］.職大學(xué)報，2009，4（3）：34-35.

〔編輯：劉曉芳〕

O212.1

：A

10.15913/j.cnki.kjycx.2017.16.022

2095－6835（2017）16－0022－03