地籍測量中光纖陀螺傾角測量技術及誤差分析

郝春玲

(渤海船舶職業學院機電工程系，遼寧葫蘆島125100)

地籍測量中光纖陀螺傾角測量技術及誤差分析

郝春玲*

(渤海船舶職業學院機電工程系，遼寧葫蘆島125100)

為了解決傳統地籍測量技術中所具有的低效、耗時以及受外界環境影響較大的缺點，基于傾角全方位測量理念與光纖陀螺尋找真北方技術聯合應用在地籍測量過程中，通過一系列的補償方法，使得光纖陀螺對外界誤差源影響的抵抗力增加，運用誤差分析其在地籍測量中的適用度，陀螺在精度為0.05°/h以及傾角誤差為1'的工況下，光纖陀螺的定位誤差約為

26.51 ″。結果表明了光纖陀螺傾角地籍測量的精度可以達到測量精度要求，因此是可行的。

光纖陀螺;地籍測量精度;傾斜尋北;誤差模型

近年來，我國土地用途變得極為廣泛，而隨著我國經濟發展進程的不斷加快，土地價值亦呈現出逐年上升的趨勢，在實際地籍測量過程中普遍采用全球定位系統(GPS)對土地測量進行過程中，對待測量土地范圍進行定點定向處理，對待測土地進行邊界定位［1-3］。

在土地測量確定點位時，在測量環境較為復雜的時候，傳統的測量定位方法并不能實現準確、穩定快速的布置土地邊界測量分布點位圖，此種方法欲想精確定位一個邊界點，需要幾個人對樣本點位進行反復移動［4-6］，效率大大降低，基于傳統的RTK測量界定土地邊界時，任何一個建筑物均會對其測量精度造成較大的影響，并且被測土地范圍內的電信信號亦會對其產生干擾，形成測量噪聲，這些均會使得傳統測量方法的測量時間大大增加，并且在傳統測量技術中，需要的x、y軸進行找平，如果被測土地表面不平，亦會對測量精度造成較大的影響［7-9］。

綜上，本文結合地籍測量的實際特點，基于光纖陀螺測量中的傾角理論來對土地邊界進行測定，分析地籍測量系統中所存在的誤差以及定位測量精度，以實現光纖陀螺測量技術對其進行全傾角狀態下的精確測量。

1 技術設計

光纖陀螺利用Sagnac效應，只是各自所采用的位相或頻率解調方式不同，或者對光纖陀螺的噪聲補償方法不同。當環行光路繞垂直于所在平面并通過環心的軸以角速度旋轉時，則沿順、逆時針方向傳播的兩波列光波在環路中傳播一周產生的相位差為［10］:

式中，ΔΦR為兩束光的相位差，c為光速，L為光纖長度，D為光纖環直徑，λ為波長，ω為旋轉角速度，A為光傳播路徑包圍的面積的向量表達。

光纖陀螺的工作原理是基于薩格納克(Sagnac)效應。薩納克效應是相對慣性空間轉動的閉環光路中所傳播光的一種普遍的相關效應，即在同一閉合光路中從同一光源發出的兩束特征相等的光，以相反的方向進行傳播，最后匯合到同一探測點，如圖1所示。

若繞垂直于閉合光路所在平面的軸線，相對慣性空間存在著轉動角速度，則正、反方向傳播的光束走過的光程不同，就產生光程差，其光程差與旋轉的角速度成正比。因而只要知道了光程差及與之相應的相位差的信息，即可得到旋轉角速度。

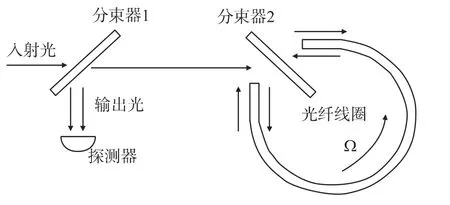
圖1 光纖陀螺儀工作示意圖

框架式陀螺儀由內框架和外框架組成，二者相互正交，均為撓性軸。檢測質量固定在內框架上。檢測質量繞驅動軸振動，由于振動角很小，故檢測質量點的振動可認為是沿輸出軸的線振動。當有角速度輸入時，哥氏力作用在檢測質量上，使其繞輸出軸振動，測量電容差值的變化，得到正比于輸入角速度的輸出電壓信號。其硬件構成和安裝示意圖如圖2所示。

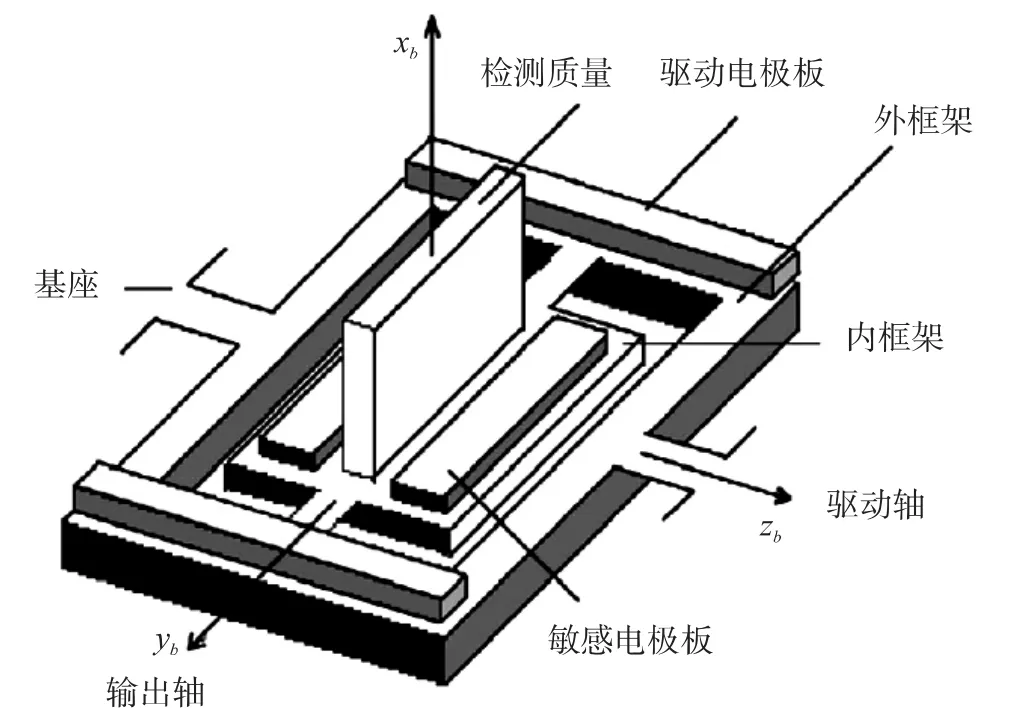
圖2 硬件構成及安裝示意圖

本文在光纖環中人為地引入一非互易的補償相移，以抵消由于光纖環旋轉產生的Sagnac相移，補償相移與Sagnac相移大小相等，方向相反。光纖陀螺始終工作在靈敏度最高的零位相差點附近，可以從補償相移中獲得陀螺的輸出信號，這時陀螺的動態范圍取決于引入補償位相的器件性能。光纖陀螺避免了陀螺輸出的非線性，動態范圍廣，檢測精度高。并且能夠自動調整優化狀態，進行動態探測追蹤。

1.1 光纖陀螺的尋北原理

光纖陀螺可以完全實現快速準確的進行尋北定位［11］，基于自動測量地球自轉所產生的周期性角速度以及地球引力所產生的重力加速度的具體值，通過對光纖陀螺參考坐標軸測得的參考方向與實際北方所夾的角度進行自動解算，從而計算出測得的某一特定軸與真北方所夾的角度進而確定出待測土地邊界的實際情況。

1.2 相關坐標系及其變換

將地球的三維坐標系變換為實測土地的三維坐標系，假設一實際坐標系OX0Y0Z0與實際地球坐標的初始點重合，在一系列的軸向運動以后的地球實際坐標系與本文假設坐標系一致，如圖3所示。H、θ、γ為各坐標軸上的轉動角度(歐拉角度)，此坐標轉換的順序可由余弦矩陣表示:

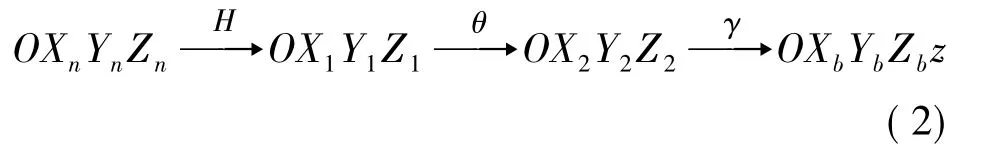
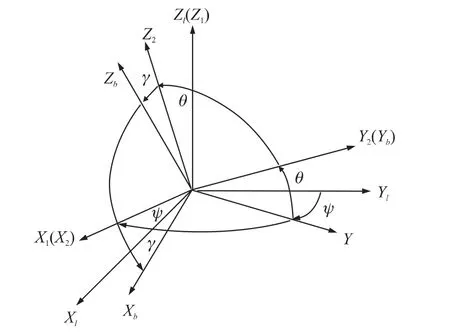
圖3 坐標系變換示意圖

OXlYlZl的各個坐標軸圍著OZl轉動的角度為H，完成第1步坐標變換，得到新的OX1Y1Z1坐標系，因此坐標變換表達式為:

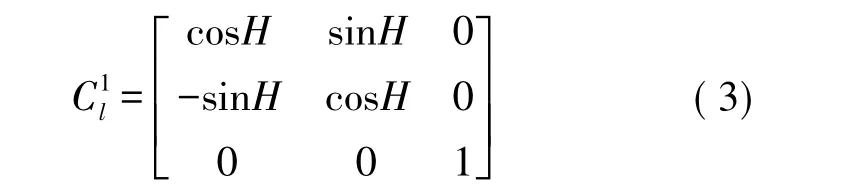
OX1Y1Z1的各個坐標軸圍著OXl轉動的角度為H，完成第1步坐標變換，得到新的OX2Y2Z2坐標系，因此坐標變換表達式為:

因此，OXlYlZl坐標系變換到載體坐標系OXbYbZb的變換表達式為:

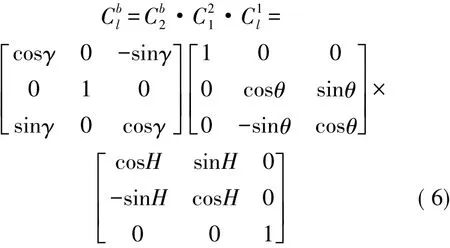
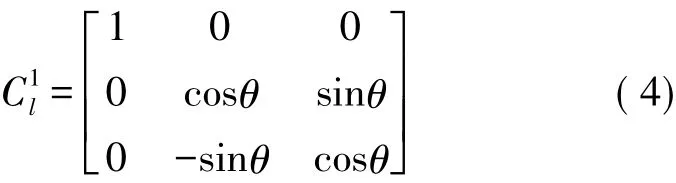
OX2Y2Z2坐標系轉換到載體坐標系OXbYbZb的變換表達式為:

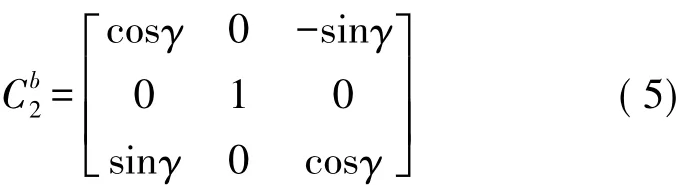
上式中基于矩陣運算的乘法法則為:

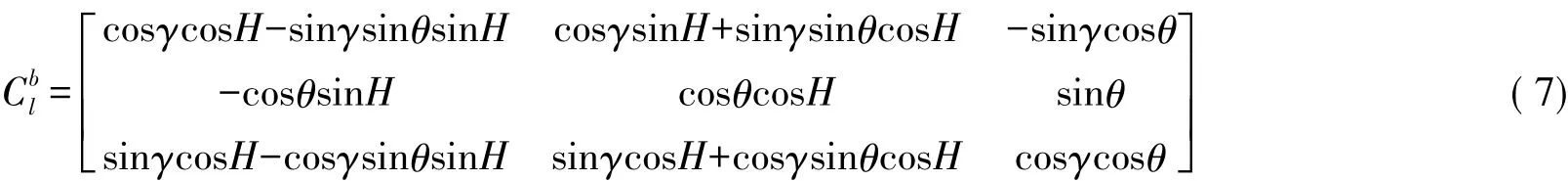
式中，H為運動方向角，θ為傾斜角，γ為橫向運動角［12］。

然而，在實際的土地測量工作中，光纖陀螺在尋找真北方時進行解算時具有多種方法，但是解算過程中的基本理論是一致的。

在實際土地測量時，把光纖陀螺在三維坐標軸的轉臺上進行固定，在安裝時應確保光纖陀螺的初始軸與載體坐標軸OYb重合，保持一致。光纖陀螺的采集信息敏感坐標軸與OYl之間的夾角角度為L，L為載體坐標系的偏北角［13］，如圖4所示。亦或可說成光纖陀螺信息采集坐標軸與真北向之間所夾的角度。

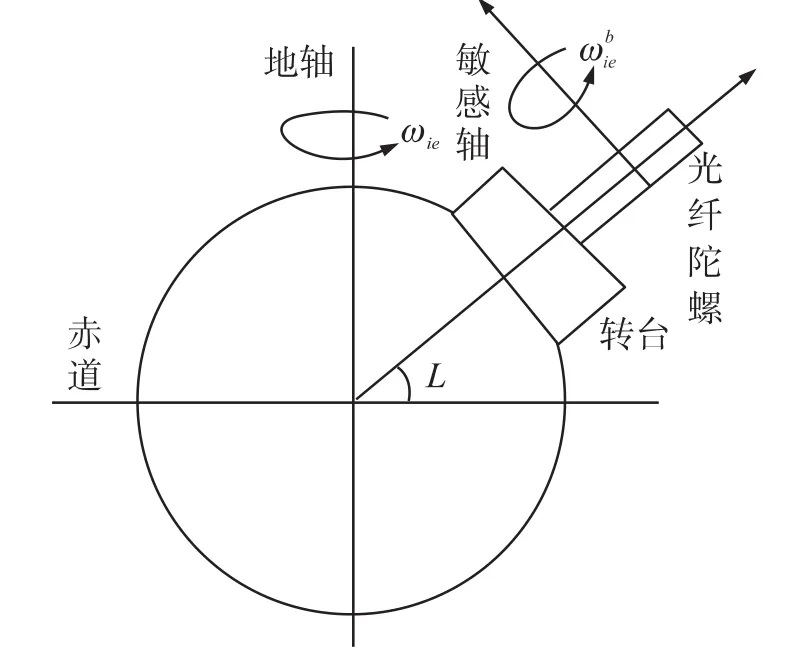
圖4 尋北原理示意圖

設定在地籍測量中的信息采集坐標軸在x-y坐標軸內，并且與載體坐標系中的y軸方向相同，其對于地球自轉產生的角速度變化較為敏感，因此，在理想測量工況下光纖陀螺的輸出表達式為:式中，ωie為地球自轉的角速度，L為被測位置所處的緯度。

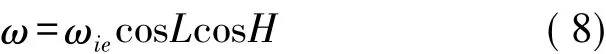
基于解算方法即可得到載體坐標系中的y軸方向與真北向所夾的角度，并且此種方法可直接確定出真北方，以此為基礎即可實現自動確定方向。

1.3 傾斜尋北解算過程

測量地球重力加速度具體值的加速度計可以十分敏感的感應測量到重力加速度［14］，其在地球坐標系中存在的各方向的分量表達式為:

矩陣經過旋轉變換得到的重力加速度在載體坐標系中的矢量分量的表達式為:

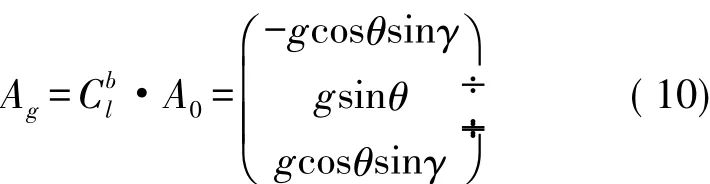
而安裝光纖陀螺測量到的重力加速度在x向以及y向的分量表達式為:綜上可得到:

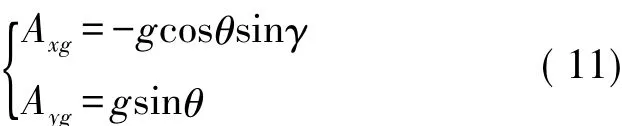
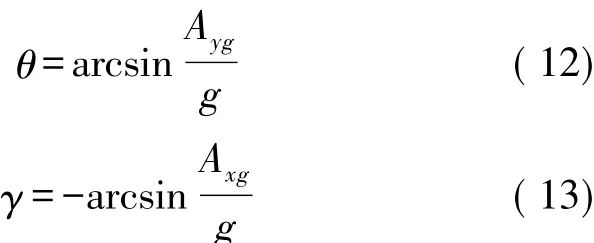
地球實際坐標系轉換為實際被測載體的矩陣表達式為:

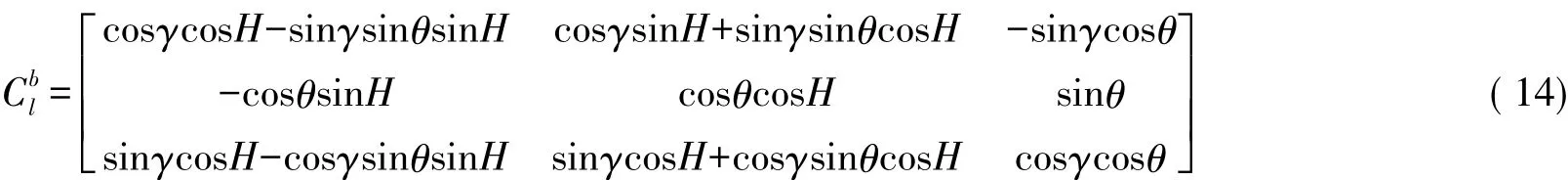
當安裝光纖陀螺的固定臺保持不動時，地球自轉所產生的角速度在被測載體坐標系內部的投影表達式為:

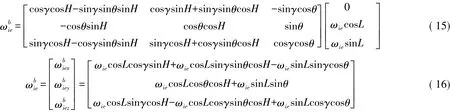
式中，由于角θ，γ角度極小，因此sinγsinθ均為高階無窮小量，即可忽略不計。由此可得光纖陀螺測得的載體角速度為:

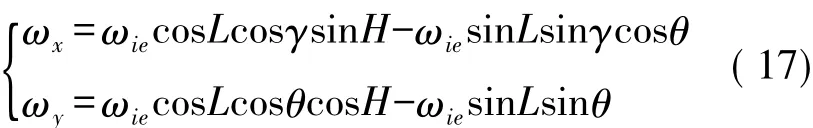
光纖陀螺在尋真北過程中的輸出表達式為:

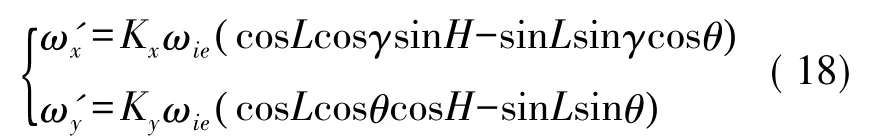
式中，忽略光纖陀螺自身產生的漂移產生的誤差，即可得到尋真北方的表達式:

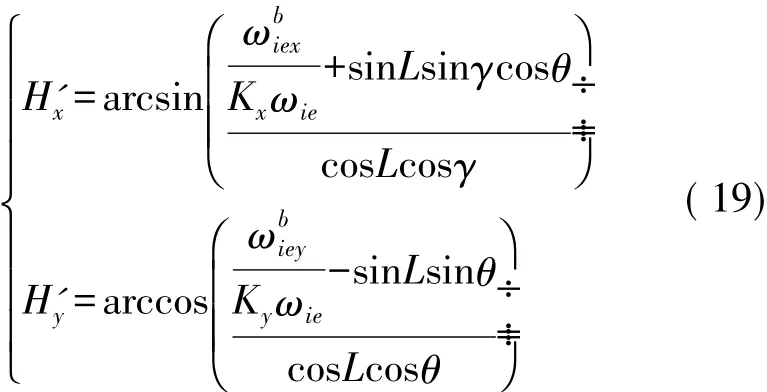
θ，γ均可忽略，即可得到:

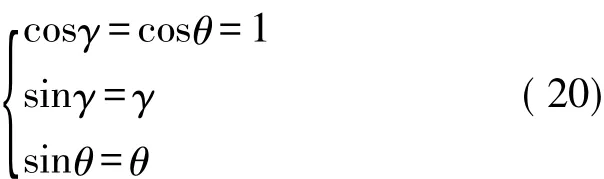
因此:

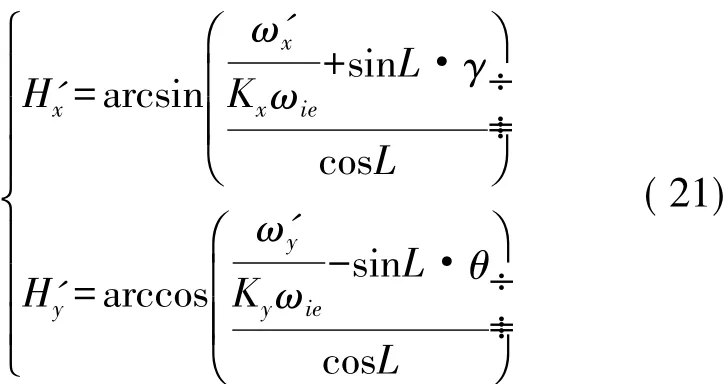
式中，H'x，H'y分別為解算出的尋真北所得的北方夾角。

2 系統誤差分析

光纖陀螺尋北定位系統所產生的誤差源主要由安裝過程引起的誤差、傾斜角度測量精度、陀螺產生漂移、轉動以及其他不可預知的一系列外界干擾源。而安裝誤差作為上述誤差源中的主要誤差［15-16］。

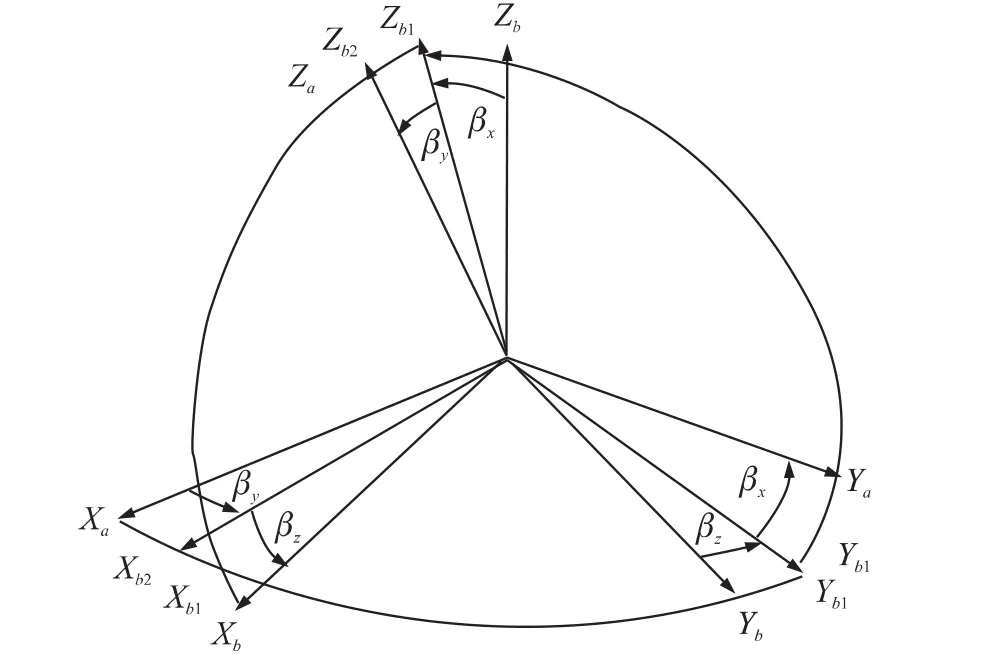
圖5 光纖陀螺與全站儀主要軸系圖

綜上所述，光纖陀螺測量到的自轉角速度在坐標系中的分量表達式為:

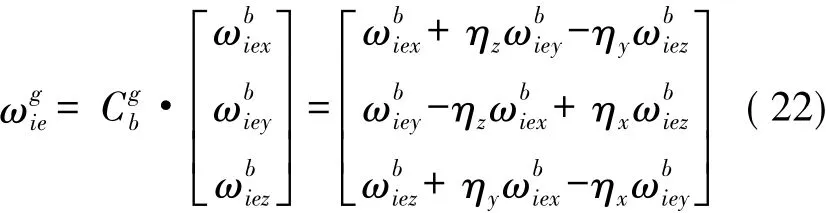
光纖陀螺在b坐標系轉換到r坐標系中的表達矩陣為:

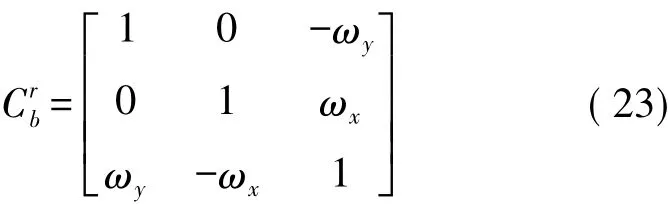
光纖陀螺固定臺進行轉動180°運行，受到轉位誤差的影響，固定臺實際的轉位角度為180°+ω2，舍掉二階無窮小量以后基于三角展開公式可得:

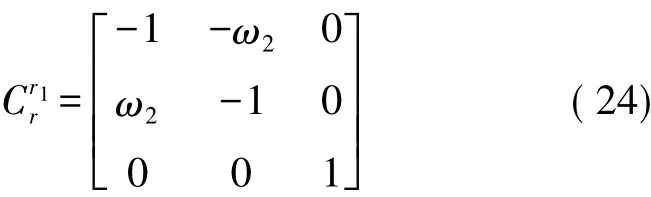
綜上，矢量角度轉換公式為:

則有:

綜上，即可求得光纖陀螺實際的安裝以及轉動誤差，并且此誤差等同于光纖陀螺的漂移，由下式可知其與ηz，ω2，ωy以及北向角H之間的關系較大。

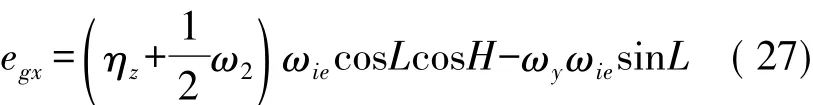
由此可見，在實際測量中，補償位置的適當增加，即可行之有效的避免光纖陀螺在安裝時所產生的安裝誤差，此過程亦避免了再一次的對光纖陀螺進行標定，節約了光纖陀螺的工作時間。

圖6為光纖陀螺在測量過程中產生的漂移現象對其測量精度以及定位精確度的影響示意圖，此過程是基于上述的解算算法計算得到的。

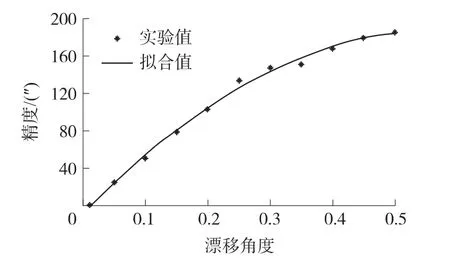
圖6 陀螺漂移對定向精度的影響

忽略并去掉其他影響光纖陀螺的小誤差源，假定光纖陀螺安裝時所產生的漂移誤差幅度為0.05 °/h，基于上述計算公式，可得到光纖陀螺在初始方向位置角度不同時，其定位精度的變化情況，見圖7。

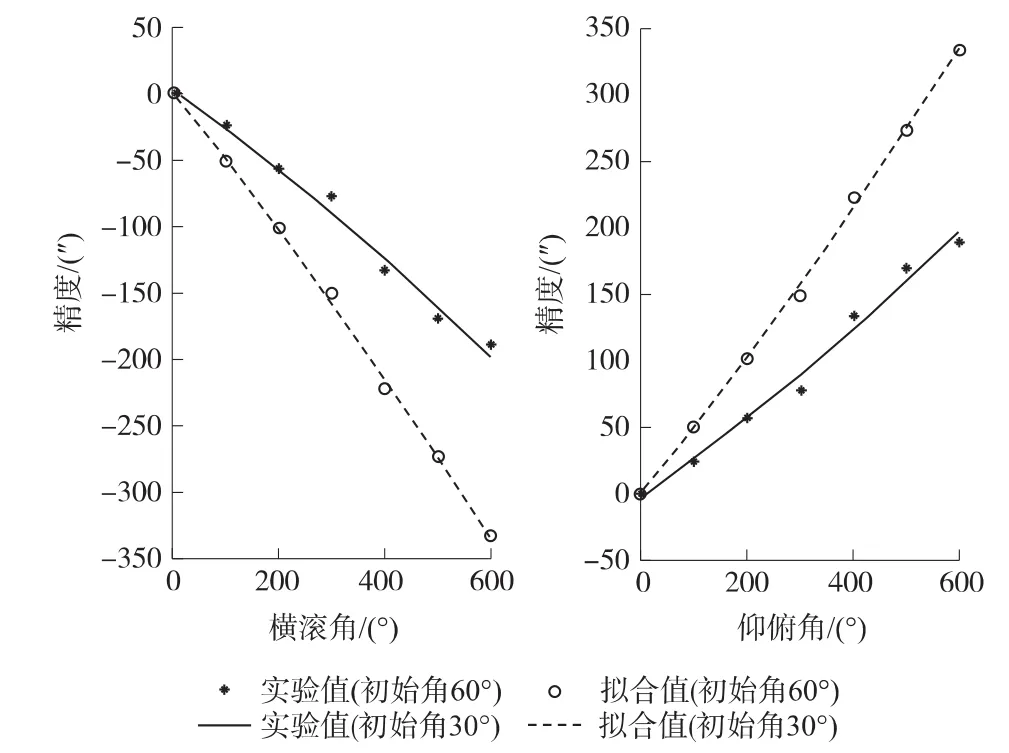
圖7 傾斜角對定向精度的影響

圖7表明光纖陀螺的定位精度隨著其定位初始角的增加而大幅增加，亦表明了本文算法的精度較高，實驗值與擬合值符合度較好，這也說明了本文的解算算法能夠提高光纖陀螺的定位精度。

3 總結

基于目前地籍測量過程普遍采用全站儀進行，這種測量技術需要耗費大量的人力物力財力，big且其定位測量精度受外界環境影響較大，并且影響其測量定位精度的因素較多，本文將現有的光纖陀螺融入了傾角測量定位技術并且結合了真北方定位技術理念，此技術在地籍測量定位過程中的精度較高，亦可大大的提高地籍定位測量的工作效率，節約大量的人力，并且不需要對待測量定位的土地進行規整，結合誤差理論對其進行誤差分析，并找到影響光纖陀螺精度的主要誤差源，并對其進行實驗研究以及仿真測試研究，將二者結果進行對比分析結果表明地位測量傳感器的精度對陀螺的地籍測量中的定位精度具有極大的影響，因此應首先選取精度較高的傳感器，而初始點的選取亦尤為重要，隨著初始角的增大，光纖陀螺的定位精度變小，因此，在采用此類定位測量技術進行地籍界定時，應選取最適合的高精度傳感器以及最優化的初始位置。

［1］劉東坡.光纖陀螺快速高精度尋北技術與實驗研究［D］.南京:南京航空航天大學，2007:21-24.

［2］張志君.基于光纖陀螺尋北定向技術研究［D］.中國科學院，2005:34-35.

［3］白云超，劉思偉，田育民，等.高精度尋北儀的現狀及發展趨勢［J］.測繪科學與工程，2008，28(4):52-56.

［4］劉毅然.基于光纖陀螺尋北系統的研究［D］.哈爾濱:哈爾濱工程大學.2007:12-13.

［5］石仕杰.光纖陀螺尋北技術研究［D］.國防科學技術大學，2004:17-22.

［6］張彤，崔一平.集成光學國際研究進展［J］.電子器件，2004，27 (1):197-198.

［7］張桂才.光纖陀螺原理與技術［M］.北京:國防工業出版社，2008:180-184.

［8］曹鮮花，吳美平，胡小萍.Matlab在光纖陀螺隨機建模中的應用［J］.航天控制，2007，25(1):18-20.

［9］田雙太，宋全軍.葛運建.基于慣性測量單元的數字鐵餅設計及數據處理算法研究［J］.傳感技術學報，2010，23(10):1516-1517.

［10］孫楠翔.光纖陀螺捷聯航姿系統去噪研究和設計［D］.哈爾濱:哈爾濱工業大學，2007:24-28.

［11］席晉.加速度計數據采集系統的研究設計［D］.哈爾濱:哈爾濱工程大學，2009:34-35.

［12］李春虹.擾動基座下激光陀螺尋北儀的數據處理研究［D］.國防科學技術大學，2006:14.

［13］Beni Prier.North-Finding Module(NFM)Navigation［J］.The Second International Symposium on Inertial Technology，1998:152-159.

［14］Budkin V L，Redkin S P.Gyro Compassing on a Movable Object by Means of Angular Rate Sensor on the Basis of DynamicallyTuned Gyro［J］.The Second International Symposium on Inertial Technology，1998:143-151.

［15］Merhav J.A Nongyroscopic Inertial Measurement Unit［J］.Journal of Guidance，1982，5(3):227-235.

［16］Watson W S.Improved North Seeking Gyro［C］//Proceeding of IEEE PLANS’9 Position［J］.Location and Navigation Symposium，1992:121-125.

［17］TD/T1001.2012地籍調查規程［S］.

郝春玲(1978-)，女，黑龍江人，漢族，大學本科，工程碩士，副教授，渤海船舶職業學院機電工程系，專業教師，研究方向為機械自動化，shenqiuv@163.com。

Cadastral New M ethod for M easuring Based on the Level Sensor_FOG_TS Combination

HAO Chunling*

(Bohai Shipbuilding Vocational College，Huludao Liaoning 125000，China)

In order to solve the problems of measurement techniques which has inefficient，time-consuming and observing environmental impact seriously defective.The technology of FOG north finding was combined with inclination measurement which will be used in cadastration.It gives steps of misalignment self-compensating of FOG;And it reduce errors in fiber optic gyroscopes(FOG)to improve its performance.FOG accuracy 0.05°/h in case，when the angle measurement error of 1'，the directional error is 26.51″.The results show the practice has proved that the FOGmeasurement’s precision can meet the request.

FOG;cadastral survey accuracy;slope north finding;errormodel

C:7630

10.3969/j.issn.1005－9490.2017.01.029

P24

:A

:1005－9490(2017)01－0152－06

2015-10-26修改日期:2016-07-29