基于LPC的共振峰檢測改進算法

韓芳，鄭晶晶

（黃河科技學院 信息工程學院，河南 鄭州 450063）

基于LPC的共振峰檢測改進算法

韓芳，鄭晶晶

（黃河科技學院 信息工程學院，河南 鄭州 450063）

語音共振峰檢測是語音處理中的一個重要組成部分，為了更好的對語音信號的共振峰進行提取，采用LPC方法，通過對LPC算法的參數調整，分割語音信號并計算出總幀數，通過改進的LPC計算出每幀的共振峰值和整個語音的共振峰軌跡。利用MATLAB進行實驗仿真，結果表明改進的LPC法在對連續語音共振峰檢測時減少了誤差，而且在信噪比小于15 dB時仍能提取出共振峰。

信號模型；倒譜法；LPC；共振峰；魯棒性

共振峰是語音信號最重要的特征參數之一，是指人在發聲時氣流通過聲道引起聲道振動而產生的一組共振頻率。共振峰參數有共振峰頻率和頻帶的寬度，語音頻譜的包絡中包含了共振峰的信息，譜包絡中的極大值就是共振峰，由于共振峰受到虛假峰值、共振峰合并、高音調語音的影響，要精確的對共振峰估計是件比較困難的事情[1-4]。

目前，常用的共振峰提取方法有倒譜法[5-6]和線性預測分析（LPC）法[7-10]。前者認為在頻域以功率譜形式出現的極大值點也就是共振峰的頻率，在功率譜中檢測出現的極大值點所對應的頻率即可[5]；后者認為用LPC對信號進行解卷積，得到聲道響應的全極點模型，并通過Newton-Raphson方法確定系統模型，取得共振峰中心頻率。文獻[11]提出的LPC法主要有兩個途徑一個是LPC求根法，一個是LPC內插法，求根法只適用于所有根都為共軛復根的情況，由于收斂速度慢，難以快速準確的找到根；文獻[12-13]提出了倒譜法檢測共振峰，利用倒譜濾波器將聲道的倒譜進行分離，并對其做相應的反變換，得到聲道函數的對數譜，進而得到共振峰，此方法會受到合并共振峰和偽峰的影響，檢測結果不精確。以上提到的倒譜法和LPC法檢測共振峰主要都是對一幀語音進行分析，實際用它們對連續語音檢測的時候還會有不少問題，為了解決虛假峰值、共振峰的合并和高音調語音的影響不少研究人員做了很多的工作，但是還沒有特別成熟的方法，文中通過對LPC求根法改進，提出一種基于LPC的連續語音共振峰檢測算法，并從魯棒性驗證該算法的有效性。

1 信號模型

線性預測分析就是將信號看作某一個模型的輸出，可以用模型參數來描述信號[14-15]。圖1中u（n）表示模型的輸入，x（n）表示模型的輸出。當 x（n）為確定性信號時模型的輸入u（n）可采用單位沖激序列；當x（n）為隨機性信號時 u（n）可采用白噪聲序列。

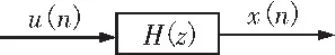
圖1 信號x（n）的模型化表示

模型的傳遞函數H（z）可以寫成有理分式的形式：

式中，系數ak、bk及增益因子G就是模型的參數；而p和q是選定模型的階數。

根據式（1），可得模型輸入與輸出之間的時域關系為:

式（4）是線性常系數差分方程。它表示模型的輸出是模型過去的輸入以及當前的輸入和過去輸出的線性組合。這可以得出，當模型的參數設計好以后就能用模型的輸入和過去的信號值來估算當前的信號值。

1）全極點模型。 在式（1）中，如果當 b1，b2，…，bq全為零，即：

2）全零點模型。 在式（1）中，如果 a1，a2，…，ap全為零，那么公式（1）和公式（4）為：

H（z）為移動平均模型（MA 模型）。

3）既有極點又有零點的模型。在式（1）中，若a1，a2，…ap，b1，b2，…，bq不全為零，則 H（z）為自回歸-移動平均模型（ARMA模型）。

2LPC求根法

用線性預測分析估計共振峰的方法有兩種：1）對全極模型公式H（z）的分母進行因式分解，找到復根，得到共振峰。2）峰值檢測法[16]。下面按照峰值檢測法對共振峰進行分析。

假設一幀語音信號x（n）可有式（5）的差分方程式表示，相應的聲道傳遞函數H（z）可用式 H（z）=表示。 以 z-1=exp（-jωT）h或z-1=exp（-j2πf/fs）代入式取功率譜模值，用 P（f）表示利用FFT方法可對任意頻率求得它的功率譜幅度響應，并從幅值響應中找到共振峰的信息。

設設任意復根 zi=riejθi， 那么共軛值 z*i=rie-jθi

也是它的根。設與zi對應的共振峰頻率為Fi，3 dB帶寬為Bi，則 Fi和 Bi與 zi如下表示：2πTFi=θie-BiπT=ri，T 表示采樣周期，于是：Fi=θi/（2πT） Bi=-lnri/πT。

3 改進LPC算法

在LPC求根法的基礎上適當調整判斷共振峰的條件，對整個語音信號進行處理，然后通過多次計算，每次計算時將語音信號分割成不同的幀數，然后利用LPC求根法計算出共振峰，最后進行平均，給出平均后的共振峰值。求共振峰的具體步驟如下：

1）求出語音信號的總幀數，采樣頻率及LPC階數；

2）根據幀數計算出幀長；

3）讀取每一幀的數據；

4）根據LPC求根法計算出3個共振峰的值；

5）判斷是否是最后一幀，如果是最后一幀則輸出共振峰的值，如果不是最后一幀則從第3）步開始執行。

改進的LPC算法詳細流程圖如圖2所示。

圖2 算法流程圖

4 實驗仿真

4.1 實驗結果分析

在MATLAB下對算法性能進行仿真實驗。實驗語音源選取1組連續元音 “a-i-u”，此純凈語音是在安靜的實驗室環境下錄制完成。采樣頻率為8 000 Hz，16比特量化編碼，語音為wav格式，采用漢明窗進行分幀，取幀長200點，幀移80點。通過MATLAB2009對連續語音用簡單LPC法進行仿真，LPC法檢測的結果圖如圖3，由圖看出共振峰頻率分布較為分散，該共振峰估計算法準確度不夠，本文提出的LPC改進檢測算法的結果如圖4，從該算法的語譜圖中看出共振峰頻率分布相對于簡單LPC法更為集中，共振峰的穩定性高于LPC法，通過語譜圖反應的結果初步得出結論：LPC改進算法共振峰估計準確性高于簡單的LPC法。連續語音“a-i-u”實驗得出的共振峰頻率值如表1～表3所示，在此，以表2為例：第一個共振峰頻率值LPC求根法誤差11 Hz，改進的LPC法誤差6 Hz，第二個共振峰頻率值LPC求根法誤差236 Hz，改進的LPC法誤差181 Hz，第三個共振峰頻率值LPC法誤差高達170 Hz，改進的LPC法誤差92 Hz，結合以上數據：各個對應的共振峰頻率LPC法的誤差都高于改進的LPC法。

圖3 LPC求根法

圖4 改進的LPC法

表1 元音a的實驗結果對比

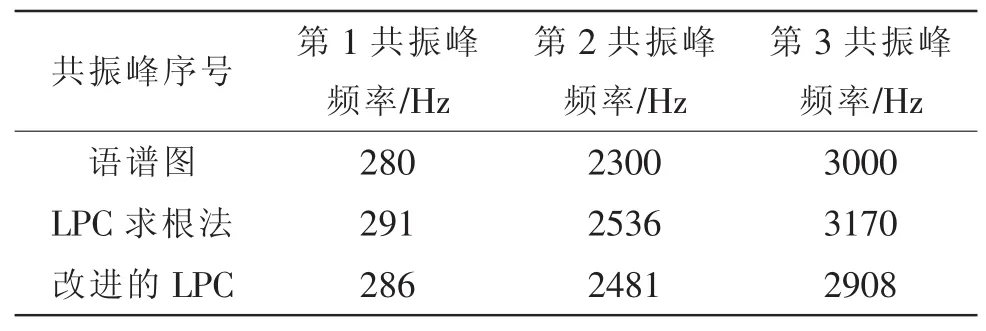
表2 元音i的實驗結果對比

表3 元音u的實驗結果對比

4.2 算法魯棒性分析

為了驗證所提方法的魯棒性，對選取的連續語音“a-i-u”作進一步分析，對該連續語音分別加入信噪比為10dB，15dB，30dB間隔不斷遞增的噪聲，經過實驗仿真，對比本文提出改進的LPC方法與簡單LPC求根法比較它們檢測共振峰估計算法的準確性。

圖5～圖6為不同信噪比下語音仿真結果圖。從仿真圖中，可以比較清晰的看出：隨著信噪比的增大，語譜圖中的白色曲線變得更有規律性，分布更加穩定，當信噪比為10 dB時，語譜圖中的白色曲線分布曲折凌亂，也很難識別具體的共振峰，當信噪比達到15 dB以上時，白色曲線的分布規律趨于穩定，共振峰的峰值分布也清晰可辨。表4～表6為不同信噪比下元音的共振峰估計結果。以表4為例在表中數據可以看出，當信噪比大于15 dB時，3個共振峰的估計誤差分別為22 Hz、100 Hz、273 Hz，當信噪比小于 10 dB 時，噪聲頻率基本淹沒測試語音頻譜，峰值無法辨別。改進的LPC法在信噪比10 dB以上有較好的魯棒性。

圖5 本文改進的算法（SNR=10 dB）

圖6 本文改進的算法（SNR=15 dB）

表4 不同信噪比下元音a的共振峰估計結果（Hz）

表5 不同信噪比下元音i的共振峰估計結果（Hz）

表6 不同信噪比下元音u的共振峰估計結果（Hz）

5 結束語

文中針對簡單的LPC共振峰檢測算法存在的不足，提出了改進的LPC法實現對連續語音進行檢測，經過加噪處理檢測算法魯棒性可知，在相對合理的信噪比下，改進的LPC法有較好的魯棒性，一旦信噪比超出合理區間，該結果將不再具有現實意義。最終的仿真結果證明在連續語音共振峰檢測的過程中，改進的LPC算法是一種相對比較優的估計算法，但是就目前研究技術與水平所限，并不能很好的檢測連續語音，存在的些許不足需待以后進一步改進和完善。

[1]王坤赤，蔣華.一種基于語音頻譜的基頻和共振峰提取算法[J].信息技術，2007，20（10）:20－22.

[2]楊丹，姜占才，余鎣良，等.語音信號共振峰提取方法的研究分析[J].科技信息，2012（4）:161-162.

[3]趙濤濤.語音信號共振峰提取算法的研究 [D].蘭州：西北師范大學，2014:4-8.

[4]趙濤濤，楊鴻武.結合EMD和加權Mel倒譜的語音共振峰提取算法[J].計算機工程與應用，2015，51（9）:207-212.

[5]David Gerhard.Pitch Extraction and Fundamental Frequency:History and Current Techniques[J].Technical Report TR-CS 2003，6（11）:1-22.

[6]趙毅，尹雪飛，陳克安.一種新的基于倒譜的共振峰頻率檢測算法[J].應用聲學，2010，29（6）:416-424.

[7]何峰，陳曉清，李國鎖，等.一種新的語音信號共振峰提取算法[J].信號處理，2007，23（4）:618－621.

[8]Lutz Welling，Hermann Ney.Formant estimation for speech recognition [J].IEEE Transactionson Speech and Audio Processing，1998，6（1）:36-48.[9]Stephanie S.Mccandless.An algorithm for automatic formant extraction using linear prediction spectra[J].IEEE Transactions on Acoustics，Speech and Processing.1974，22（2）:135-141.

[10]Codello I，Kuniszyk-Jozkowiak W.Formant paths tracking using linear prediction based methods[J].Annales UMCS Informatica AI，2010，10（2）:7-12.

[11]郁伯康，郁梅.LPC方法提取語音信號共振峰的分析[J].電聲技術，2003，3（1）:3－8.

[12]趙力.語音信號處理[M].北京：機械工業出版社，200:61－65.

[13]王曉亞.倒譜在語音基音和共振峰提取中的應用[J].無線電工程，2004，34（1）:57－61.

[14]羅艷芬.語音信號數字處理中語音編解碼算法的研究[M].南昌：南昌大學，2005.

[15]宋瑞，詹舒波.語音情緒識別中的共振峰特征分析[J].中國科技論文在線，2014.

[16]楊鴻武，趙濤濤.一種基于加權Mel倒譜的語音信號共振峰提取算法 [J].西北師范大學學報，2014，50（1）:53-57.

Improved resonance peak detection alogrithm based on LPC

HAN Fang，ZHENG Jing-jing
（The School of Information Engineering，HUANGHE S&T COLLEGE，Zhengzhou 450063，China）

Formants extraction from speech signal is an important part of speech processing，in order to extract the formants of speech signal，By using LPC method and adjusting parameters of the LPC method，dividing the speech signal and calculating the total number of frames，the formants of each frame and the entire speech signal is calculated by improved LPC.Large numbers of simulation experiments in MATLAB show that the improved LPC can reduce errors of the continuous speech formant detection，when signal-to-noise ratio is less than 15 dB，the improved method still can extract the formants.

signal model；cepstrum；LPC；formant;robustness

TN912.3

A

1674－6236（2017）17-0085-05

2016-07-07稿件編號：201607061

鄭州市科技局科技發展計劃項目 （20140663）；鄭州市嵌入式系統應用技術重點實驗室建設項目（121PYFZX177）；鄭州市教學質量工程項目（zzlg201608）

韓 芳（1981—），女，河南新鄉人，碩士，副教授。研究方向：信號處理，計算機網絡等。