Matlab在多元函數積分計算中的應用研究

楊真真

摘 要：Matlab作為目前使用最為廣泛的科學計算類軟件之一，被廣泛應用于工程計算、控制設計等諸多領域。針對多元積分學中的重積分、曲線積分和曲面積分計算等問題，在多元函數積分運算教學中利用Matlab進行輔助教學，以激發學生學習興趣，加深其對所學知識的理解，提高教學效果。

關鍵詞：三重積分；曲線積分；曲面積分；Matlab；多元函數

DOIDOI：10.11907/rjdk.171983

中圖分類號：TP319

文獻標識碼：A 文章編號文章編號：1672-7800（2017）008-0149-04

0 引言

隨著“互聯網+”和大數據技術的蓬勃發展，當今社會已進入全民信息時代[1]，傳統的“粉筆—黑板”式的教學已不再適應時代發展。高等數學教學也在教授學生基本知識的同時，引入Matlab進行輔助教學[2-5]。在高等數學教學中，多元函數積分學是高等數學的重點和難點，它涉及的概念、性質和公式十分復雜，包括重積分、曲線積分和曲面積分3大部分內容[6-8]，學生往往把握不住重點，有些內容難以區分，計算時更是無從下手。因此，如何激發學生學習興趣，提高教學效果，成為高校教授高等數學課程教師關注的重點。

眾所周知，多元函數積分計算的總體思想是轉化為定積分進行計算，例如將重積分轉化為累次積分，將曲線積分根據曲線方程轉化為定積分，然后將曲面積分根據曲面方程轉化為重積分，進而再轉化為定積分。在多元函數積分的具體計算中，要想快速順利地計算出正確結果，除了掌握定積分轉化思想外，還要注意換元法、格林公式、高斯公式和斯托克斯公式等的合理運用。

為了提高教學效果，激發學生學習興趣，本文在多元函數積分學的重積分、曲線積分和曲面積分的計算教學中利用Matlab進行輔助教學，以加深學生對多元函數積分學計算方法的理解。在高等數學教學中，利用Matlab進行輔助教學，不僅給學生提供了一個快速有效的計算結果檢驗工具，讓其看到數學理論不是那么枯燥無味，還可以使用數學軟件進行處理，而且讓其認識到Matlab的強大功能，為后期學生進行數學實驗、參加數學建模競賽打下基礎。

1 利用Matlab進行三重積分計算

三重積分是高等數學教學中的難點和重點，計算三重積分的方法是將其轉化為累次積分。三重積分的計算方法分為直角坐標系下三重積分的計算方法、柱面坐標系下三重積分的計算方法和球面坐標系下三重積分的計算方法，其中直角坐標系下三重積分的計算方法又分為“投影法”和“截面法”[9-10]。“投影法”是先對某一變量進行積分，然后對其余兩個變量的二重積分進行計算。如果三重積分的被積函數是一元函數，或某兩個變量的二重積分容易積出時，采用“截面法”更為簡單。

三重積分的計算由于方法和形式多樣，學生學習過程中很難區分各種計算方法。此外，由于三重積分的積分區域是立體圖形，部分學生的空間想象力不是很好，將給三重積分的計算帶來很大困難。因此，在三重積分計算中采用Matlab進行輔助教學，讓學生在熟悉三重積分計算方法的同時，能夠對積分區域進行可視化，從而使學生領略到Matlab的魅力，激發其學習興趣。下面通過例題1介紹采用Matlab求給定函數在給定區域的三重積分。

例1 計算三重積分I=Ωzdxdydz，其中Ω由曲面z=x2+y2，z=1，z=2所圍成。首先用Matlab畫出積分區域Ω：z=x2+y2，z=1，z=2的立體圖形，讓學生對曲面Ω有個可視化的認識，其程序代碼如下，積分區域圖形如圖1所示。x=-1.2：0.01：1.2； y=x； [X，Y]=meshgrid（x，y）； Z1=X.∧2+Y.∧2； mesh（X，Y，Z1）； hold on Z2=ones（size（X））； mesh（X，Y，Z2）； hold on Z3=2* ones（size（X））；mesh（X，Y，Z3）； hold off xlabel（′x軸′）； ylabel（′y軸′）；zlabel（′z軸′）；

解法一：在直角坐標系下先將三重積分轉化為累次積分：I=Ωzdxdydz=4[∫20dx ∫2-x20dy ∫2x2+y2zdz -∫10dx ∫1-x20dy ∫1x2+y2zdz ]其程序代碼如下：syms x y z； I1=int（int（int（z，z，x∧2+y∧2，2），y，0，sqrt（2-x∧2）），x，0，sqrt（2））； I2=int（int（int（z，z，x∧2+y∧2，1），y，0，sqrt（1-x∧2）），x，0，1）； I=4*（I1-I2）其輸出為：I =（7*pi）/3。解法二：在柱面坐標系下有：I=Ωzdxdydz=∫2π0dθ ∫20dr ∫2r2rzdz -∫2π0dθ ∫10dr ∫1r2rzdz 其程序代碼如下：syms r theta z； I1=int（int（int（r*z，z，r∧2，2），r，0，sqrt（2）），theta，0，2*pi）；I2=int（int（int（r*z，z， r∧2，1），r，0，1），theta，0，2*pi）； I=I1-I2其輸出為：I =（7*pi）/3。因此，I=Ωzdxdydz=7π3。

2 利用Matlab計算曲線積分

曲線積分分為第一類曲線積分和第二類曲線積分，其計算思想都是將曲線積分根據曲線方程轉化為定積分[11-12]。第一類曲線積分的計算主要通過積分路徑曲線的參數方程，將其轉化為定積分。其中，選擇合適的積分路徑曲線參數方程是解題的關鍵。第一類曲線積分的積分路徑和方向無關，轉化為定積分時，積分下限總小于積分上限；第二類曲線積分的計算稍為復雜，分為直接計算和間接計算兩類計算方法。直接計算法，也即通過積分路徑的參數方程將第二類曲線積分轉化為定積分進行計算，因為第二類曲線積分和積分路徑的方向有關，轉化成的定積分下限對應積分路徑曲線的起點，上限對應積分路徑曲線的終點。間接計算主要指利用兩類曲線積分的聯系以及格林公式來計算第二類曲線積分。下面分別通過例2、例3介紹在曲線積分的計算中引入Matlab進行輔助教學。例2 求曲線積分I=∮L（x2+y2）ds，其中曲線L為x2+y2=2x在第一象限的部分。解：設曲線L的參數方程為x=1+cost，y=sint （0≤t≤2π），則dx=-sintdt，dy=costdt，ds=dx2+dy2=sin2t+cos2tdt=dt，于是：∮L（x2+y2）ds=∮L2xds=∫2π02（1+cost）dt =4π現用Matlab驗證計算結果的正確性，其程序代碼如下：endprint

syms t； x=（1+cos（t））； y=sin（t）； dx=diff（x，t）； dy=diff（y，t）； ds=sqrt（dx∧2+dy∧2）； f=x∧2+y∧2； I=int（f*ds，t，0，2*pi）輸出為：I =4*pi。例3 求曲線積分I=∮L（x-y）dx+（x+y）dyx2+y2，其中曲線L為圓周x2+y2=a2按逆時針方向繞行。解：設曲線L的參數方程為x=acost，y=asint，t為0～2π，dx=-asintdt，dy=acostdt，因此有：I=∮L（x-y）dx+（x+y）dyx2+y2=∫2π0a（cost-sint）·（-asint）+a（cost+sint）·acosta2dt =∫2π0dt =2π現用Matlab驗證計算結果的正確性，其程序代碼如下：

syms a t； x = a*cos（t）； y = a*sin（t）； f =[（x-y）/（x∧2+y∧2），（x+y）/（x∧2+y∧2）]；ds =[diff（x，t）； diff（y，t）]； I = int（f*ds，t，0，2*pi）其輸出為：I =2*pi。

3 利用Matlab計算曲面積分

曲面積分分為第一類曲面積分和第二類曲面積分，其計算思想都是將曲面積分根據曲面方程轉化為二重積分[13-15]。第一類曲面積分的計算主要通過曲面在適當坐標平面的投影轉化為二重積分進行計算，選擇合適的坐標平面投影是解題關鍵，注意投影面積不能為零；第二類曲面積分的計算分為直接計算和間接計算兩種，其中直接計算是指通過積分曲面向坐標平面投影將第二類曲面積分轉化為二重積分進行計算，投影方向是固定的，投影面積可以為零。由于第二類曲面積分的積分曲面是有方向的，一定要注意積分曲面的側面，從而確定二重積分相應的符號。間接計算主要指利用兩類曲面積分的聯系以及高斯公式來計算第二類曲面積分。下面分別通過例4、例5介紹在曲面積分的計算中引入Matlab進行輔助教學。例4 計算曲面積分I=ΣdSz，其中Σ是球面x2+y2+z2=4被平面z=1截出的頂部。首先用Matlab畫出積分區域Σ，其程序代碼和積分區域的圖形如下所示：x1=-2：0.01：2； y1=x1； [X1，Y1]=meshgrid（x1，y1）； Z1= ones（size（X1））； mesh（X1，Y1，Z1）； hold ont=linspace（0，pi，25）；p=linspace（0，2*pi，25）； [theta，phi]=meshgrid（t，p）； x=2*sin（theta）.*sin（phi）；y=2*sin（theta）.*cos（phi）； z=2*cos（theta）； surf（x，y，z）； xlabel（′x軸′）；ylabel（′y軸′）；zlabel（′z軸′）；

解：Σ的方程為z=4-x2-y2，投影區域為Dxy：x2+y2≤3，故有：dS=1+z2x+z2y=24-x2-y2dxdy于是有：I=ΣdSz=Dxy24-x2-y2dxdy=Dxy2r4-r2drdθ=2∫2π0dθ ∫30r4-r2dr .其程序代碼如下：syms r theta； I= int（int（2*r/（4-r∧2），r， 0，sqrt（3）），theta，0，2*pi）

其輸出為：I=4*pi*log（2）。因此，I=ΣdSz=4πln2。

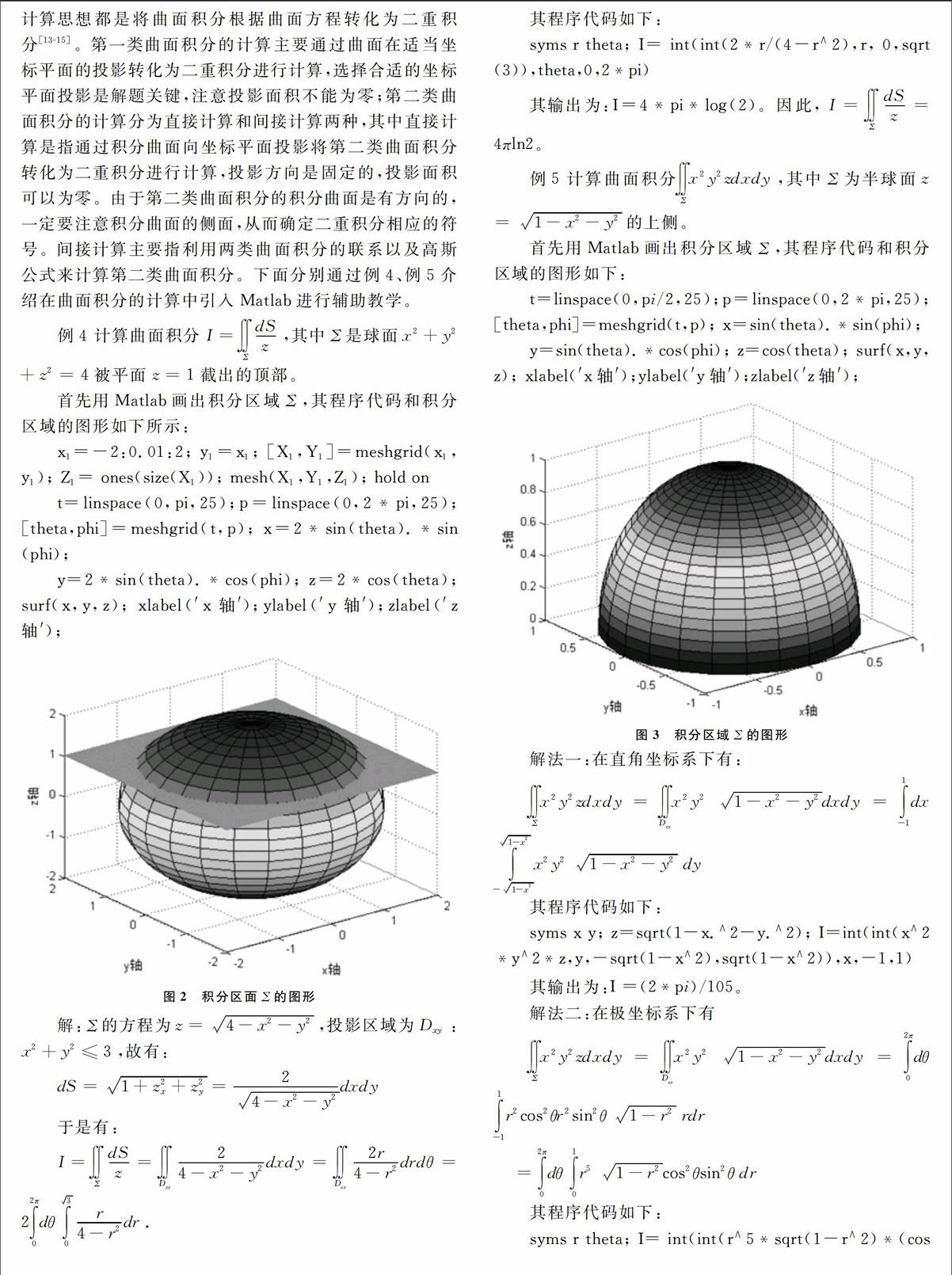
例5 計算曲面積分Σx2y2zdxdy，其中Σ為半球面z=1-x2-y2的上側。首先用Matlab畫出積分區域Σ，其程序代碼和積分區域的圖形如下：t=linspace（0，pi/2，25）；p=linspace（0，2*pi，25）； [theta，phi]=meshgrid（t，p）； x=sin（theta）.*sin（phi）； y=sin（theta）.*cos（phi）； z=cos（theta）； surf（x，y，z）； xlabel（′x軸′）；ylabel（′y軸′）；zlabel（′z軸′）；

解法一：在直角坐標系下有：Σx2y2zdxdy=Dxyx2y21-x2-y2dxdy=∫1-1dx ∫1-x2-1-x2x2y21-x2-y2 dy其程序代碼如下：syms x y； z=sqrt（1-x.∧2-y.∧2）； I=int（int（x∧2*y∧2*z，y，-sqrt（1-x∧2），sqrt（1-x∧2）），x，-1，1）其輸出為：I =（2*pi）/105。解法二：在極坐標系下有Σx2y2zdxdy=Dxyx2y21-x2-y2dxdy=∫2π0dθ ∫1-1r2cos2θr2sin2θ1-r2 rdr =∫2π0dθ ∫10r51-r2cos2θsin2θ dr其程序代碼如下：syms r theta； I= int（int（r∧5*sqrt（1-r∧2）*（cos（theta））∧2*（ sin（theta））∧2，r， 0，1），theta，0，2*pi）其輸出為：I =（2*pi）/105。因此，Σx2y2zdxdy=2π105。

4 結語

本文將Matlab 應用到多元函數積分包括三重積分、曲線積分和曲面積分的計算中，不僅給學生提供了一個檢驗計算結果正確性的方法，而且讓積分區域圖形可視化，激發了學生的學習興趣，達到了更好的教學效果。此外，在多元函數積分學的教學中使用Matlab進行輔助教學，還能培養學生使用軟件進行數學計算的能力，為學生后續參加數學建模競賽等奠定基礎。

參考文獻：

[1] 覃慶國，楊亞培，蔣寧，等.依托學科優勢構建電子信息類創新人才培養體系[J].電子科技大學學報：社會科學版， 2010， 12（5）：103-106.

[2] 唐春明，王中興.Matlab軟件在高等數學教學中的應用[J].高等數學研究， 2016， 19（1）：120-123.

[3] 李永芳.基于MATLAB軟件的高等數學實驗教學[J].高教學刊， 2017（6）：79-80.

[4] 尹云輝. MATLAB在高等數學教學中的應用[J].軟件導刊， 2011， 10（5）：173-174.

[5] 王秋亮.關于MATLAB在高等數學教學中的應用分析[J].軟件導刊：教育技術， 2016， 15（3）：3-5.

[6] 趙洪牛，等.高等數學（下） [M].北京：高等教育出版社，2010：58-170.

[7] 同濟大學應用數學系.高等數學（上） [M].第7版.北京：高等教育出版社，2014.

[8] 南京郵電大學高等數學教研室.高等數學同步學習指導[M].北京：高等教育出版社，2013：231-295.

[9] 張輝，李應岐，陳春梅.三重積分的計算方法[J].課程教育研究：學法教法研究， 2016（3）：233-234.

[10] 仇海全，潘花.MATLAB在重積分計算中的應用[J].重慶工商大學學報：自然科學版， 2012， 29（4）：50-54.

[11] 張輝，李應岐，敬斌，等.第一類曲線積分的計算方法[J].高等數學研究， 2015， 18（2）：27-29.

[12] 景慧麗，趙偉舟，楊寶珍，等.第二類平面曲線積分的計算探討[J].蘭州文理學院學報：自然科學版， 2012， 26（6）：99-102.

[13] 張輝，李應岐，趙偉舟，等.第一類曲面積分的計算方法[J].高等數學研究， 2014（2）：44-46.

[14] 楊雯靖.第二類曲面積分的計算方法探討[J].數學學習與研究， 2015（17）：93-94.

[15] 魏光美，馮偉杰.第二類曲面積分的計算方法[J].高等數學研究， 2012， 15（4）：104-106.endprint