車隊離散模型的最佳統計時間研究

于 泉 梁 銳 郭增增

(北京工業大學城市交通學院 北京 100124)

車隊離散模型的最佳統計時間研究

于 泉 梁 銳 郭增增

(北京工業大學城市交通學院 北京 100124)

為對車隊離散模型進行精度驗證，尋找出最適合模型驗證的數據的統計方法，選擇對適合城市道路交叉口之間路段的Robertson提出的車隊離散模型進行研究.采用多點攝像法對北京市五條路段的交通流進行實地調查，將交通流數據按照1～36 s不同的時間間隔進行統計，并在不同的統計間隔下分別驗證Robertson提出的車隊離散模型，得出該模型在1～36 s不同的統計間隔下的誤差.對誤差的均值和方差以及百分比進行數學分析，從而得出該模型中調查數據的最佳統計時間為6～10 s，并采用T檢驗法進一步驗證了該結論.

交通控制；車隊離散；最佳統計時間；信號優化

0 引 言

在城市道路中,停車線處的排隊車輛在綠燈開啟時，并不是統一啟動統一出發，而是由于行駛速度的不同，逐一駛離停車線，車隊之間的距離也在這個過程中逐漸增大，車輛逐漸分散，車隊在經過排隊后駛離停車線的這種變化稱之為車隊離散.國內外有許多學者研究了車隊的離散模型.

Pacey[1]假定車輛在上游停車線駛向下游過程中車速是不變的，但各車速度不同，而且每一種車速的分布頻率是符合正態分布規律的.Vincent等[2]認為路段中行駛的車輛在兩個斷面之間行駛速度的差異導致了行駛時間的不同，而行駛時間是按照幾何函數來分布的，由此提出了幾何分布模型.Giulio等[3]通過研究相鄰路口之間距離的變化產生的影響，對車隊離散模型和細胞傳輸模型進行了比較，并利用兩個優化算法：Hill Climbing算法和Simulated Annealing算法得到仿真結果.

王殿海等[4]建立了一種基于無變換正態分布的車隊離散模型，同時根據不同位置的檢測數據和車隊離散模型提出了流量反饋機制預測方法，通過驗證表明了這種方法可以提高流量預測的精度.史麗平等[5]為了分析車隊離散模型在實際中的適用性,考慮左轉影響下車隊的離散特性,建立左轉影響下直行車的離散模型，并以北京市調查數據為基礎,利用實際數據對離散模型進行驗證.孫瑋瑋等[6]利用Vissim仿真軟件對線控系統進行仿真，對比路段長度變化前后的車隊離散數據，并改變路段上車流的分布函數，得到車流分布與車隊離散特性之間的關系.

上述研究主要是圍繞建立一種新的車隊離散模型或者是對現有的車隊離散模型進行分析和改進.隨著現代科技的進步以及數據采集裝置的不斷更新，采集數據的精度已按秒計算，在對車隊離散模型進行分析研究時，對數據采集與處理的要求也越來越高，而國內外文獻均欠缺對于數據采集和處理的精細度方面的研究[7-9].本文以車隊離散模型的相關數據為出發點，研究采用最佳的統計時間間隔對調查數據進行統計，使其在對車隊離散模型進行計算或驗證時得到誤差最小、精度最高的結果.鑒于Robertson模型適用于較短距離的行駛時間分布，比較適合城市中兩交叉口之間的情況，本文選擇了Robertson的幾何分布模型進行研究.

1 車隊離散模型介紹

車隊離散的幾何分布模型,即路段中行駛的車輛在兩個斷面之間行駛速度的差異導致了行駛時間的不同，而行駛時間是按照幾何函數來分布的，造成了路段上下游斷面的車輛到達率為

qd(i+t)=Fq0(i)+(1-F)qd(i+t-1)(1)

式中：qd(i+t)為第(i+t)個時段，下游某斷面上預計的車輛到達率；q0(i)為第i個時段，上游停車線斷面的車輛通過率；t為上述兩個斷面之間，車輛平均行駛時間的80%(以時段數為單位)；F為車流離散系數，其計算式為

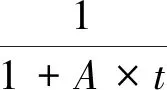
(2)

式中：A為根據觀察值修正，通常取0.35.

統計時間T是在驗證Robertson幾何分布模型的精度時，提出的一個概念.上述幾何分布模型中的通過率以及到達率均需要在實際的交通調查中獲得，統計時間T是在統計通過率與到達率的數據時，采用的不同的時間間隔進行統計[10-11].由于近幾年智能交通控制系統的快速發展，交通控制中數據采集裝置的精度已經按秒計算，又考慮到統計時間不宜超過綠燈時長，因此本文將通過率與到達率的相關數據按照1～36 s不同的統計時間進行統計，然后分別進行模型的精度驗證.

2 數據采集

交通特性的研究離不開道路交叉口數據的實地調查，在車隊離散特性研究中，現場觀察數據是后期分析工作的第一手資料，通過現場觀測與分析，才能掌握交通特性的基本變化規律[12-13].本次調查選取了北京市的五個路段，在非高峰時期對五條路段的交通流進行觀測，前四條路段和錄像情況見表1.

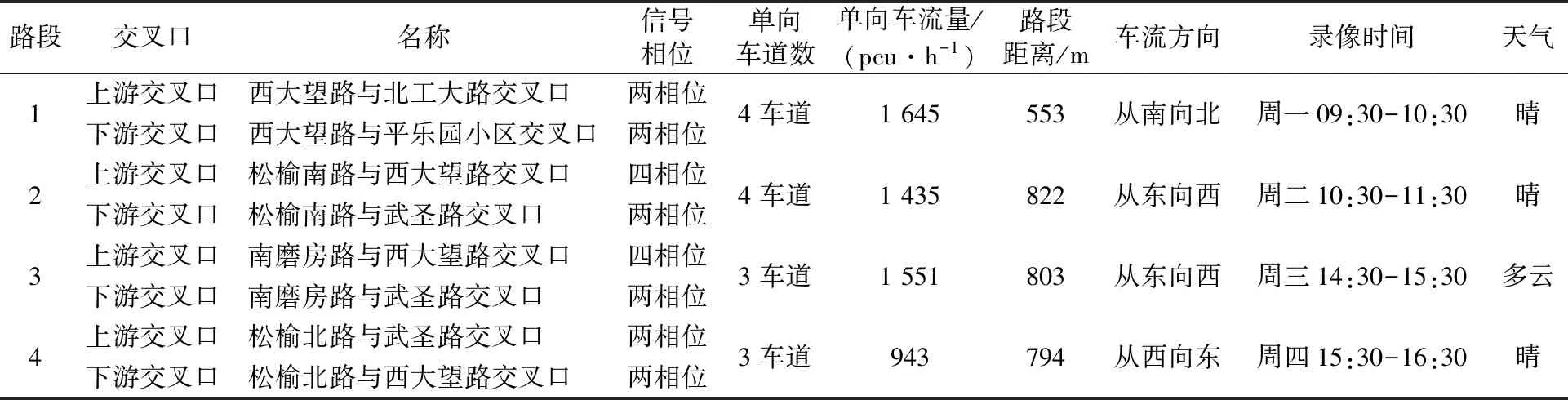
表1 路段和錄像情況表

分別用攝像機錄下同一路段上游交叉口車輛的通過情況和下游交叉口車輛的到達情況，由于錄像機具有時間記錄功能，這樣就可以從視頻里獲得四個路段上游和下游分別的流量數據，以路段1為例，在統計時間T分別為1～36 s的情況下，路段1的部分現場調查數據上游車輛通過率(q0(i))和下游車輛到達率(qd(i+t-1))、經Robertson的幾何分布模型計算得出的路段1的下游某斷面預計車輛到達率(qd(i+t))以及到達率誤差數據，限篇幅表略.

3 最佳統計時間研究

為了對Robertson的幾何分布模型進行更細致的精度驗證，并且分析出最佳統計時間，本文在統計時間T分別為1～36 s時，對所得到的計算數據與實際數據的誤差進行數學分析，得出四個路段的每一組誤差數據的均值，見圖1.

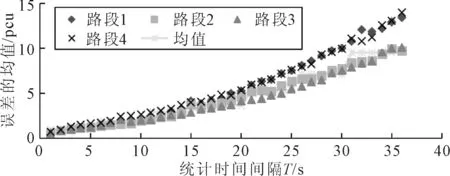
圖1 誤差的均值分析散點圖

由圖1可知，各個路段的誤差的均值都是隨著統計時間T的增大而逐漸增大.當統計時間T=1 s時，路段1的誤差均值為0.55，路段2的誤差均值為0.51，路段3的誤差均值為0.58，路段4的誤差均值為0.66.當統計時間T=5 s時，路段1的誤差均值為1.16，路段2的誤差均值為1.2，路段3的誤差均值為1.17，路段4的誤差均值為1.45.當統計時間T=36 s時，路段1的誤差均值為13.4，路段2的誤差均值為9.71，路段3的誤差均值為10.01，路段4的誤差均值為13.97.為了更清晰的體現均值的變化，現將四個路段的均值按照每5 s一次的統計時間間隔再取均值，圖形在圖1中用黑色加粗線段表示，數據見表2.

表2 誤差的均值分析表

由表2可知，在統計時間T=1～5 s時，四個路段的誤差均值均保持在一輛車以下，隨著統計時間T的增加，誤差均值逐漸增加至3，7輛車，當統計時間T=30～36 s時，誤差均值已經增加至10輛車.說明統計時間T越小，得到的數據在帶入Robertson的車隊離散模型計算后，與實際數據對比的誤差越小，越有利于對離散模型的精度驗證.為了進一步對各個路段調查數據與計算數據之間誤差的波動性進行研究，本文對各組誤差的方差進行了數學分析，見圖2.

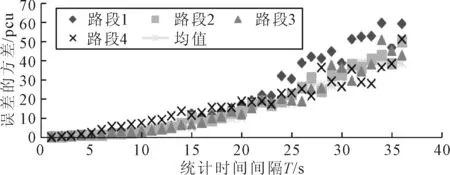
圖2 誤差的方差分析散點圖

由圖2可知，各組誤差的方差的趨勢是隨著統計時間T的增加而逐漸增長的.當統計時間T=1 s時，路段1誤差的方差為0.4，路段2誤差的方差為0.38，路段3誤差的方差為0.5，路段4誤差的方差為0.01.當統計時間T=5 s時，路段1誤差的方差的誤差為1.14，路段2誤差的方差為1.31，路段3誤差的方差為1.46，路段4誤差的方差為2.3.當統計時間T=36 s時，路段1誤差的方差為59.52，路段2誤差的方差為50.24，路段3誤差的方差為42.08，路段4誤差的方差為51.23.為了更清晰的體現方差的變化，現將四個路段的方差按照每5 s一次的統計時間間隔再取均值，圖形在圖2中用黑色加粗線段表示，數據見表3.

表3 方差的均值分析表

由表3可知，當統計時間T=1～5 s時，四條路段的方差均值為0.32，這說明以1～5 s為統計時間間隔統計得到的數據帶入Robertson的車隊離散模型計算后，與實際數據對比的誤差的波動非常穩定，每組誤差值都接近于誤差均值，由之前的對均值的分析可知，該情況下的誤差均值均小于一輛車，即每組誤差值均小于一輛車.當統計時間T=30～36 s時，四條路段的方差均值增長至38.8，這說明以30～36 s為統計時間間隔統計得到的數據帶入Robertson的車隊離散模型計算后，與實際數據對比的誤差的波動非常大，每組誤差值的分散程度都很大，偏離誤差均值的程度大小不一，因此在統計時間T=30～36 s的情況下得到的數據不適合對離散進行精度驗證.

對以上的分析均是針對誤差的絕對值，由于統計時間間隔的增大，無法排除累計誤差的影響.因此，下面將對誤差與實際到達車輛的比值進行計算，將計算得出的36組比值取均值進行分析，見圖3.

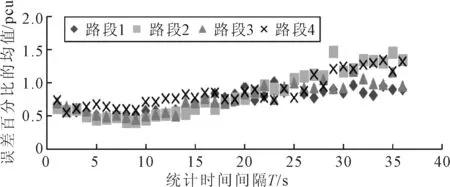
圖3 誤差的百分比的均值分析折線圖

由圖3可知，統計時間T的值越小，進行模型驗證的精度越高.當統計時間T=1～5 s時，四條路段的誤差的百分比約為65%，當統計時間T=6～10 s時，四條路段的誤差的百分比降低至約45%，當統計時間T大于10 s時，誤差的百分比呈增長趨勢，當統計時間T=36 s時，四條路段誤差百分比增長至120%，非常不利于進行精度驗證.

因為四條路段的數據采集時間均為非高峰時段，所以在對Robertson的車隊離散模型進行高精度驗證時，本文認為誤差小于兩輛車，且誤差占比小于50%才能算高精度驗證，由此，本文得出統計時間T=6～10 s時，為驗證車隊離散模型時的最佳統計時間.

4 結論驗證

本文用新采集到的路段五的數據來驗證這個結論，其中路段5的具體情況以及錄像情況見表4.

同前四條路段采集到的數據的處理方法一樣，將路段五的數據中的上游停車線斷面的車輛通過率q0(i)以及下游某斷面上前1 s的車輛到達率qd(i+t-1)分別按照6～10 s的統計時間間隔進行統計，并將統計之后的數據帶入Robertson的車隊離散模型進行計算，得出五組不同統計時間間隔下的下游某斷面上的車輛到達率qd(i+t)，限于篇幅表略.

表4 路段5及錄像情況表

本文采用數理統計學中的T檢驗來驗證上述結論，T檢驗來判定兩個組別每一種的平均值的差異是否顯著，因為T檢驗是用于小樣本，總體標準差σ未知的正態分布總體，是用于小樣本的兩個平均值差異程度的檢驗方法.它是用T分布理論來推斷差異發生的概率，從而判定兩個平均數的差異是否顯著.

將統計時間T=6～10 s時的計算數據和實際數據分別導入spss軟件，利用T檢驗分析得到的輸出結果見表5.

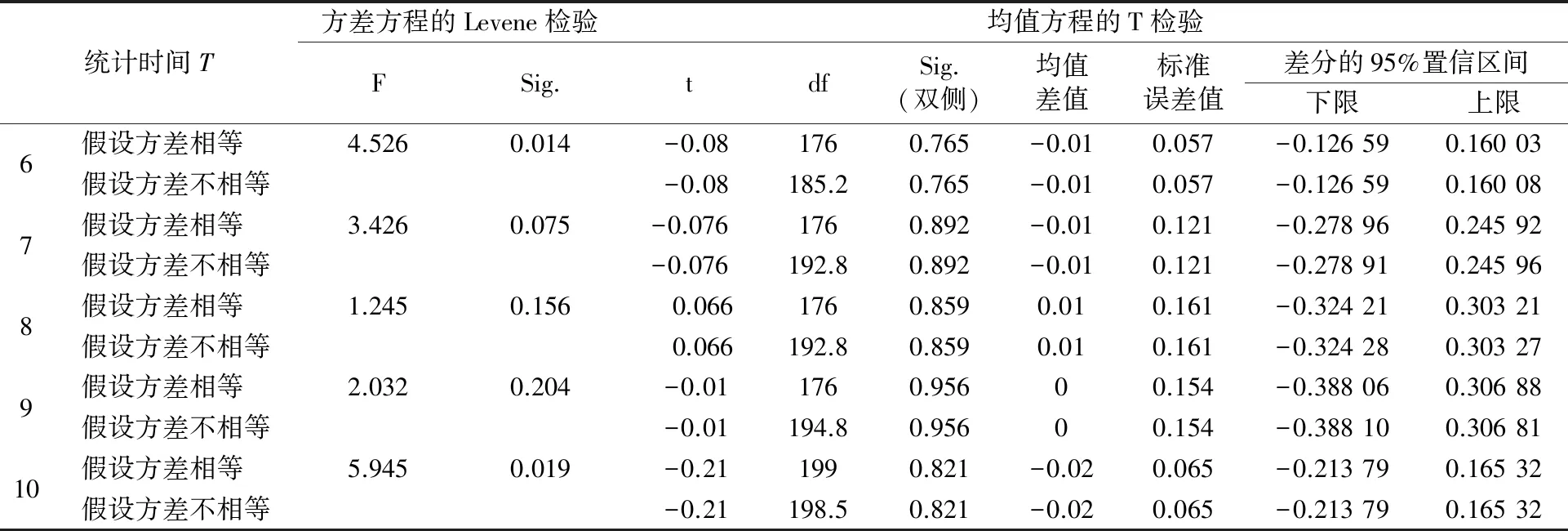
表5 獨立樣本檢驗

方差方程的Levene檢驗是做方差齊次檢驗，由表5可知，統計時間T=6～10 s時，方差方程的Levene檢驗的sig的值均大于0.01，即五組數據的計算數據與實際數據的方差無顯著性差異，而均值方程的T檢驗中的sig的值(P值)均大于5%，接收假設H0：μ1-μ2=0，認為五組數據中的計算數據與實際數據無顯著性差異.因此用統計時間T=6～10 s時的數據可對車隊離散模型進行精確的精度驗證，驗證了統計時間T=6～10 s是最佳統計時間的結論.

5 結 束 語

本文采用多點攝影法對北京市四條路段在非高峰時期的交通流進行實地調查.將交通流數據按照1～36 s不同的時間間隔進行統計，并在不同的統計間隔下分別驗證Robertson提出的車隊離散模型，得出該模型1～36 s不同的統計間隔下的誤差.通過對誤差的均值和方差進行數學分析，得出該模型中到達率與通過率的最佳統計時間T=6～10 s，并采用T檢驗法進一步驗證了該結論.該結論對于今后在對車隊離散模型進行計算或者驗證時，為交通調查數據的統計和處理提供了最直接的方法，在一定程度上對于路段上車流離散現象的研究和交叉口處的信號配時優化都有一定的積極作用，后續可對高峰時期的交通流展開更深入的研究，以便獲得更豐富的研究結果.

[1]PACEY G M. Propess of a buch of vehicles released from a traffic signal[J]. Road Research Laboratory,1956(S1):55-58.

[2]VINCENT R A, MITCHELL A I, ROBERSON D I. User guide to TRANSYT[J]. TRRL Report,1980(S1):189-195.

[3]GIULIO E C. The network signal setting problem: the coordination approach vs. the synchronisation approach[J]. Computer Modelling and Simulation,2013(2):575-579.

[4]王殿海，李鳳，宋現敏.一種新的車隊離散模型及其應用[J].吉林大學學報，2009，39(4):891-895.

[5]史麗平，于泉，劉小明，等.左轉影響下的車隊離散模型研究[J].交通標準化，2012(19):74-76.

[6]孫瑋瑋，李康，郝斌斌.基于vissim的車隊離散特性研究[J].交通科技與經濟，2015(3)：43-48.

[7]陳寧寧,何兆成,余志.考慮動態紅燈排隊消散時間的改進MAXBAND模型[J].武漢理工大學學報,2009,33(5):590-595.

[8]保利霞.基于車隊離散模型的交叉口關聯度量化方法研究與試驗[J].公路交通科技,2011,28(S1):1-8.

[9]劉燦齊，楊佩昆.信號燈交叉口車隊散布模型與信號燈協調控制[J].同濟大學學報，1996，24(6):636-641.

[10]劉燦齊，楊佩昆.車隊密度散布模型及在車隊結尾問題上的應用[J].中國公路學報，2001，14(1)：89-91.

[11]全永燊，郭繼孚，鄭猛.我國城市道路車流離散規律初探[J].城市交通，2001(1):32-35.

[12]GRACE M J. A theory of the diffusion of traffic platoons[J]. Operational Research，1964(4):255-275.

[13]GARTNER N. A demand-responsive strategy for traffic signal control[J]. Transportation Research Record,1983(6):75-84.

Research on the Best Statistical Time of Platoon Dispersion Model

YU Quan LIANG Rui GUO Zengzeng

(CollegeofMetropolitanTransportation,BeijingUniversityofTechnology,Beijing100124,China)

In order to verify the accuracy of the platoon dispersion model and find out the statistical method of data most suitable for the model validation, the platoon dispersion model proposed by Robertson is studied. This model is particularly suitable for the sections between urban road intersections. The traffic flows of five roads in Beijing city are investigated by multi-spot photography. The traffic flow data are collected at different time intervals ranging from 1 s to 36 s and are used to verify the platoon dispersion model proposed by Robertson for different statistical intervals. Finally, the errors of the model for different statistical intervals are obtained. The mean, variance and percentage of the errors are analyzed and the best statistical time of the survey data in this model is found to be 6～10 s. The conclusion is verified by the T test.

traffic control; platoon dispersion; optimal statistical time; signal optimization

2017-05-18

U491

10.3963/j.issn.2095-3844.2017.04.010

于泉(1976—)：男，博士，副教授，主要研究領域為智能交通、交通控制