集裝箱船全航線智能預配問題研究*

汪圓圓 陳順懷

(高性能船舶技術教育部重點實驗室 武漢 430063)

集裝箱船全航線智能預配問題研究*

汪圓圓 陳順懷

(高性能船舶技術教育部重點實驗室 武漢 430063)

針對掛靠多港口集裝箱船的全航線預配問題，以倒箱量最少、船舶縱向強度最優為目標，提出該問題的0-1整數規劃模型.利用基于規則的方法，并分別采用混合整數規劃算法、蟻群算法和遺傳算法求解之.結果表明，在待配載箱數較少時，混合整數規劃算法快速，且得到的解為最優解.給出了基于以上三種算法及一定的裝箱規則的全航線智能配載算法.采用該算法模擬計算得出了8 Bay集裝箱船全航線智能預配結果，保證了倒箱量為0，且考慮到了縱向強度目標，即集裝箱重心距離船舯的距離最小.

集裝箱船；預配；整數規劃；遺傳算法；蟻群算法

0 引 言

集裝箱預配問題是一類較為復雜的組合優化問題，其求解的復雜度隨集裝箱所占Bay位數的增加而呈爆炸式增長，預配需考慮如何通過合理配載使船舶具有較合理的浮態并且使船舶重量合理分布，以保障船舶的快速性和結構強度的安全.多年以來，國內外學者對此問題進行了一系列的研究.

張維英等[1-3]提出首先將集裝箱按貨物種類、尺寸和目的港組成同類箱組，以同類箱組為處理單元，以倒箱數量最少、船舶載箱率最高及不同目的港集裝箱占用Bay位數量最少為目標，以滿足船舶縱向強度和吃水差要求為約束條件，采用超尺寸裝箱完成集裝箱在船上的縱向布置，并產生配載的總布置圖.而后在預配的基礎上，針對單一目的港集裝箱和混合目的港集裝箱Bay位，分別以初穩性高度最優及橫傾力矩最小、倒箱量最少為目標，采用基于指派問題的禁忌搜索算法和隱式圖啟發式搜索算法進行求解.而其給出的全航線配載算例中，沒有賦予每個集裝箱重量，實際上得到的全航線配載結果是無意義的.

Ambrosino等[4]提出一種針對集裝箱配載問題的分解啟發式算法，將集裝箱配載問題分為三個子問題，預配問題則相當于這三個問題中的第一個問題.其采用系統的配載優化策略，運用啟發式搜索策略，在理論上解決了大型集裝箱船的配載問題.Avriel等[5]將集裝箱配載問題轉換為圖著色問題，并且證明了當Bay位列數大于4時，無能力約束倒箱問題為NP完全問題.但并未給出具體求解策略及相關算例.Araújo等[6]將Pareto前沿與聚類搜索算法相結合，提出一種Pareto聚類搜索算法(pareto clustering search,PCS)，以倒箱量最少和船舶穩定性最優為目標，得到了在船舶掛靠不同數目的港口時，采用該算法得到的前沿要優于其他兩種算法.Pacino等[7]提出一種能夠快速產生近優配載計劃的二步分解算法，采用混合整數規劃模型，松弛整數約束，使整個解產生的時間小于330 s，且解的效果良好.孫俊清等[8]討論了停泊多港口的集裝箱運輸班輪全航線配載問題，以船舶穩性為約束，倒箱量為目標，建立了0-1整數規劃模型，并采用改進的遺傳算法求解之.其優勢在于其算法的設計，而其劣勢在于對集裝箱全航線配載問題模型的建立過于簡單，沒有考慮到重量的合理分布，這顯然是不合理的.

本文將針對文獻[3]中的算例進行修改和一定的拓展，以倒箱量最少、船舶縱向強度最優為目標(模擬算例未考慮吃水差)，提出該問題的0-1整數規劃模型，并分別采用混合整數規劃算法、蟻群算法和遺傳算法求解之.結果表明，在待配載箱數較少時，混合整數規劃算法快速，且得到的解為最優解.給出了基于以上三種算法及一定裝箱規則的全航線智能預配算法，最后采用該算法模擬計算得出了8Bay集裝箱船全航線智能預配結果.

1 配載問題的數學模型

1.1 問題描述

預配即按船上Bay為裝載單元，將集裝箱按類別(如尺寸、目的港、不同種類箱等)組成同類箱組，以同類箱組為裝載單元，采用合適的裝箱算法確定同類箱組在船上縱向布置，完成配載的總布置圖，見圖1.

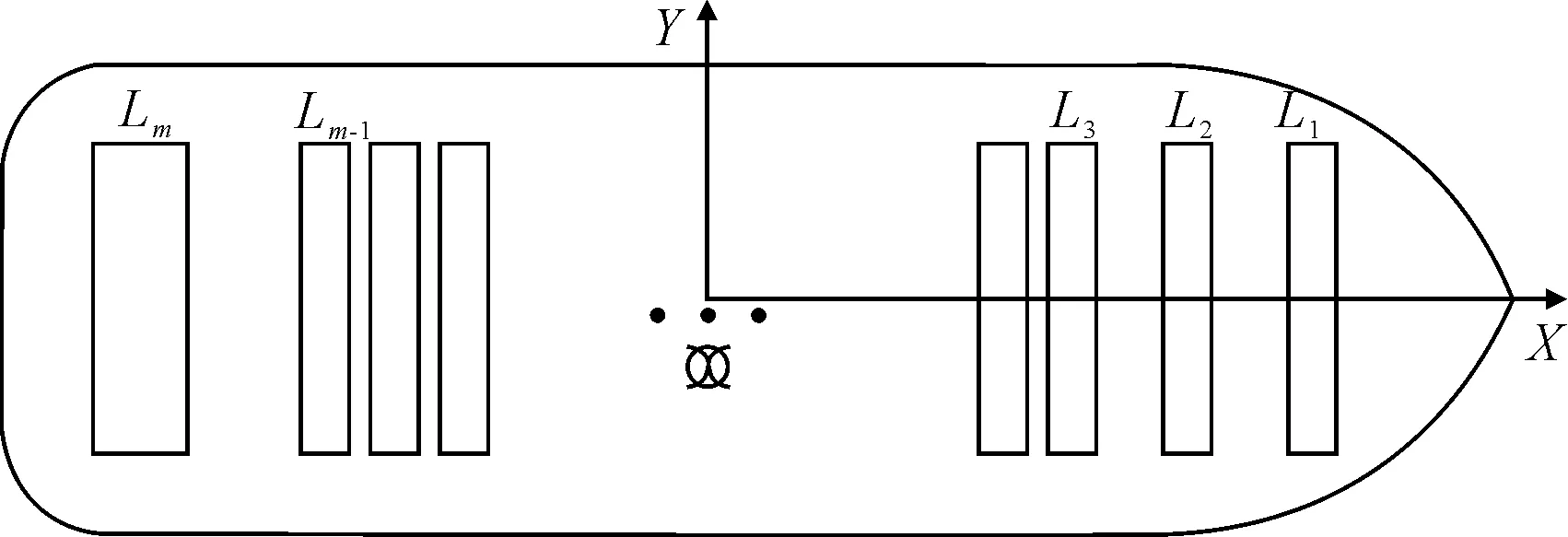
圖1 箱位排布俯視圖

在圖1中，以L1，L2，…，Lm為箱位的縱向排布順序，按自船首至船尾增序排列.其所包含的箱位數量分別為r1，r2，…，rm，距船舯的位置為x1，x2，…，xm，圖中顯示了TEU和FEU箱位的排布示意.

以t表示裝箱矩陣，即

(1)

式中：tij為裝載港為i，卸載港為j的集裝箱數量，j>i，否則tij=0，并且裝箱矩陣元素符合下述關系為

(2)

式中：tn為第n港的裝箱量.

則問題可以描述為：將tn個集裝箱配載入圖1的m個Bay位中，其中這tn個集裝箱可以分為若干個同類箱組，如何配載可使得所產生的倒箱量，即先卸載集裝箱被后卸載集裝箱壓在下面的次數最少、船舶的縱向強度最優.

1.2 數學模型的建立

假設與裝箱矩陣對應的重量矩陣為

(3)

式中：wij為裝載港為i，卸載港為j的集裝箱重量.設待配載同類箱組分別為1，2，…，n，集裝箱船Bay位號從首至尾分別為1，2，…，m，則集裝箱船預配問題即如何將這n個同類箱組配載至這m個Bay位中，使得倒箱量最少、結構強度最優.

在集裝箱全航線配載過程中，將配載變量定義為cij，表示將第i個箱組裝載于第j個Bay位，見表1.

表1 配載變量定義

在配載過程中，對于混裝Bay位，將按照先卸載港后裝，后卸載港先裝的規則，從而保證不產生倒箱量.由此，給出如下集裝箱全航線配載0-1整數規劃模型為

(4)

(5)

(6)

(7)

wi≤[w] (i=1，2，…，m)

(8)

n≤m

(9)

ti≤ri(i=1，2，…，m)

(10)

upID≤downID

(?BayID∈MixedBay)

(11)

ShiftNums≤[Nums]

(?BayID∈MixedBay)

(12)

式(4)表示所有集裝箱組對船舯的力矩越小越好，集裝箱船的總縱強度以左右集裝箱組對于船舯的力矩來表示，因此，該值越小，表示總縱強度越好.式(5)～(7)表示配載變量約束，即配載變量只能取0或者1之間的一個，且表1的任意一行、任意一列相加都要為1，即每一個箱組只能占用一個Bay位，每一個Bay位只能被一個箱組所占據.式(8)表示每一個Bay位所裝載的集裝箱重量不得超過該Bay所允許裝載的集裝箱最大重量.式(9)表示箱組個數不得超過集裝箱船的Bay位總數.式(10)表示任意箱組中的集裝箱數目不得超過其所占據的Bay位中的集裝箱箱位數量.式(11)表示對于混合Bay，卸載港編號小的集裝箱不得處于卸載港編號大的集裝箱之下，即保證先卸載港的集裝箱后裝，后卸載港的集裝箱先裝.式(12)表示在整個裝配過程產生的倒箱量不超過[Nums]，本文模擬算例將之取為0.

2 全航線智能預配算法

目前，針對全航線配載問題的算法多基于經典裝箱算法[9]，以Bay位利用率、倒箱量為目標進行配載，而后校核強度、吃水差等約束條件.本文則以強度、倒箱量為目標，并遵循若干裝卸規則，對掛靠多港口的集裝箱船全航線配載問題提出一種全航線智能預配算法.

Azevedo等[10]針對集裝箱船配載問題，提出6種裝載規則和2種卸載規則.Benedito等[11]提出在混合Bay裝載過程中，先卸載港后裝載，后卸載港先裝載的規則.利用以上這些規則，可以減小集裝箱全航線配載問題的求解難度.

全航線智能預配算法的基本步驟如下.

步驟1 將集裝箱船Bay位按自船艏至船艉進行編號，記作：BayID=1，2，…，m，其所包含的箱位數量分別為r1，r2，…，rm，距船舯的位置分別為x1，x2，…，xm.

步驟3 按上節所述0-1整數規劃模型，采用混合整數規劃算法或兩種智能算法(遺傳算法、蟻群算法)求解之，得到第1港裝載結果.

在蟻群算法求解過程中，將距離函數定義為

(13)

其他諸如概率函數、信息素更新規則等的定義與基本蟻群算法一致，且采用蟻周模型進行更新[12].

步驟4 船舶航行至第2港，先清空卸載港編號為本港的集裝箱，于其他港卸載的集裝箱保持不變，卸載完成后，更新船舶Bay位屬性，在第2港，箱子的拆分、重量的分配要視當前集裝箱對于船舯的力矩而定，規定船舯往船艏為正方向，則如果當前力矩為正值，且 需要補充箱子的Bay位位置為負，則取同一卸載港重箱進行補充；反之，取同一卸載港輕箱補充.若補充后，剩余箱子數目小于被補充Bay位原有箱子數目，則不進行補充.補充完成后，按卸載港編號從大到小進行配載，對于數量不超過Bay位容量的，作為一個箱組進行配載，對于數量超過Bay位容量的，要對其進行拆分，拆分時，要不選擇最輕箱進行拆分，要不選擇最重箱進行拆分，視當前力矩值的正負及Bay位位置而定.當有多種Bay位可選時，調用混合整數規劃算法或者智能算法求解之.如此往復，直到所有箱子都配載完畢，便得到第2港配載方案.

步驟5 對除目的港以外的其他港進行相同操作，并在目的港清空Bay位中的所有集裝箱，得到整個全航線預配方案.

3 結果與分析

假設某集裝箱船在某一航線上將要掛靠6個港口，該船上共有8個Bay位，均裝TEU，相鄰兩Bay位之間的間距都為100 mm，每一Bay位的最大容量都為46箱.另一艘集裝箱船同樣在這一航線上掛靠6個港口，該船上共有40個Bay位，亦均裝20英尺的標準箱，相鄰兩Bay位之間的間距都為100 mm，每一Bay位的最大容量都為200箱，箱子的重量有3種規格，即7，12和18 t.8 Bay集裝箱船的裝箱矩陣及與之對應的重量矩陣分別為

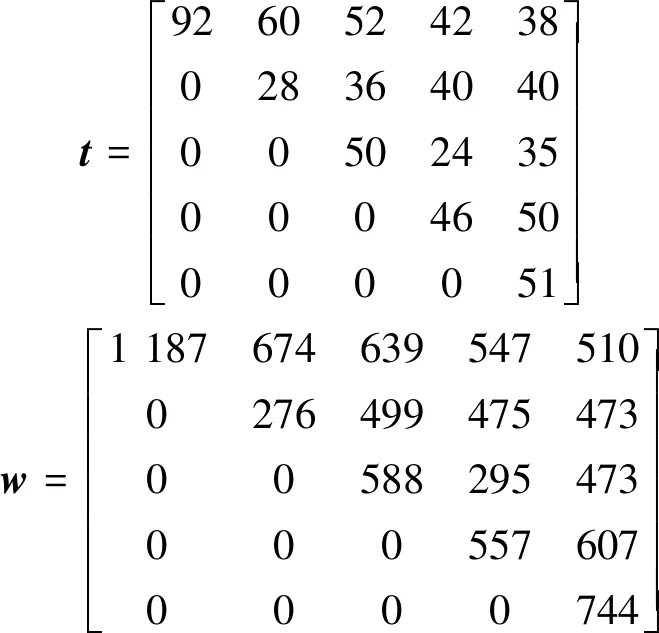
表2為三種算法對8 Bay集裝箱船在第1港口裝載后的求解結果比較.其中蟻群算法和遺傳算法都計算100代.遺傳算法中，交叉概率取0.75，變異率取0.25，種群數量取200，精英個體數取30.蟻群算法中，螞蟻數量取5，信息素啟發因子α取2，期望啟發式因子β取3，信息素揮發系數ρ取0.3，信息素常量Q取1 000.并在同一臺計算機上進行計算.

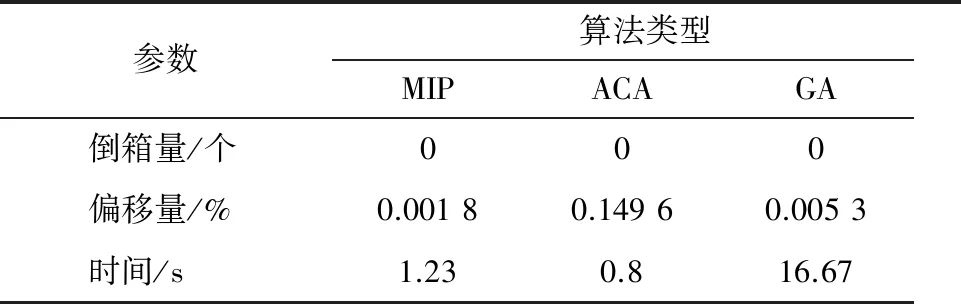
表2 不同算法的計算結果

模擬集裝箱Bay位總長為49.164 m，在各港裝載后的重心縱向偏移量見表3.按照第2部分的全航線智能預配算法，可得采用混合整數規劃求解8Bay集裝箱船的結果，見表4.

表3 重心縱向偏移量

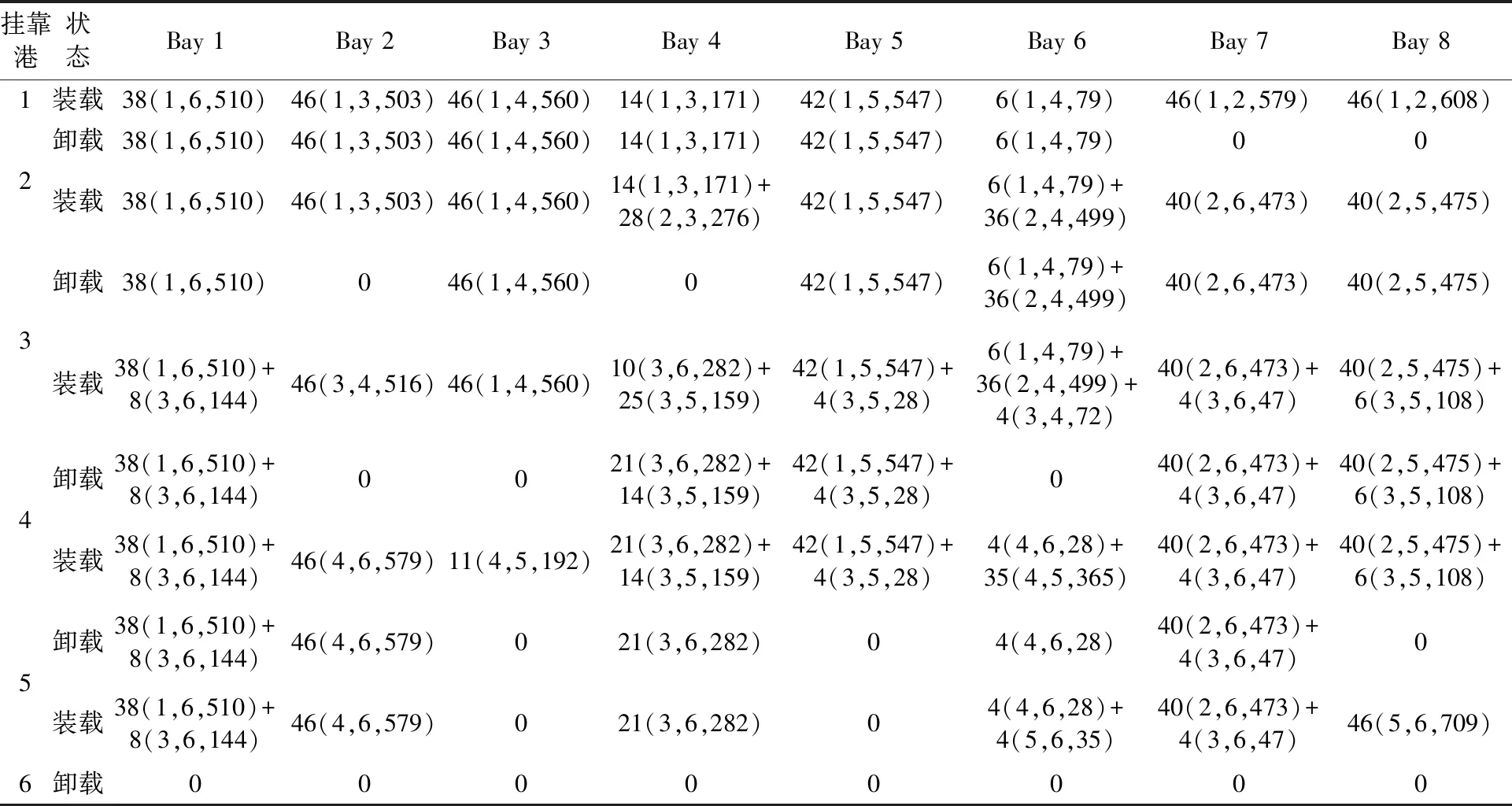
表4 全航線預配結果

注：a(i,j,w)表示裝載港為i，卸載港為j的集裝箱數量為a，重量為w；a1(i,j,w1)+a2(k,q,w2)+…，表示混裝Bay位，且按裝載順序相加.

4 結 束 語

本文針對掛靠多港口集裝箱船的全航線預配問題，采用了基于規則的方式，以倒箱量最少、船舶縱向強度最優為目標，并結合三種算法即混合整數規劃算法、蟻群算法和遺傳算法，提出了針對該問題的智能預配算法.采用該算法，可以得到船舶在首港預配的最優解及后續港預配的近似最優解.模擬實驗結果表明所提出的算法可行，為集裝箱船舶的全航線多目標預配問題提供了一個可用的模型，為Bay位排箱(進一步優化穩性與橫傾)奠定基礎.并可為其他船舶的智能配載問題作參考。

[1]張維英.集裝箱船全航線配載智能優化研究[D].大連：大連理工大學,2006.

[2]張維英,林焰,紀卓尚,等.集裝箱船全航線Bay位排箱優化模型[J].上海交通大學學報,2007,41(2):199-204.

[3]張維英,林焰,紀卓尚,等.集裝箱船全航線預配優化模型與算法研究[J].大連理工大學學報,2008,48(5):673-678.

[4]AMBROSINO D, SCIOMACHEN A, TANFANI E. A decomposition heuristics for the container ship stowage problem[J]. Journal of Heuristics,2006,12(3):211-233.

[5]AVRIEL M, PENN M, SHPIRER N. Container ship stowage problem: complexity and connection to the coloring of circle graphs[J]. Discrete Applied Mathematics,2000,103(1):271-279.

[7]PACINO D, DELGADO A, JENSEN R M, et al. Fast generation of near-optimal plans for eco-efficient stowage of large container vessels[C]∥ International Conference，2011(2):286-301.

[8]孫俊清,陳忱,劉鳳連.考慮船舶穩定性的多港口集裝箱配載問題[J].計算機工程與應用,2012,48(32):236-243.

[9]衛家駿.集裝箱船智能配載研究[D].大連：大連海事大學,2012.

[10]AZEVEDO A T D, ARRUDA E F D, NETO L L D S, et al. Solution of the 3D stochastic stowage planning for container ships through representation by rules[C]∥ International Workshop on Knowledge Discovery, Knowledge Management and Decision Support，2013:120-129.

[11]BENEDITO M P L, SANTOS A G D. Evolutionary algorithm and ant colony optimization for a container stowage problem[J]. Discrete Applied Mathematics,2015(1):55-58.

[12]汪定偉.智能優化方法[M].北京：高等教育出版社,2007.

A Research on Intelligent Pre-stowage Planning Problem for Containerships in Full Routes

WANG Yuanyuan CHEN Shunhuai

(KeyLaboratoryofHighPerformanceShipTechnology,MinistryofEducation,Wuhan430063,China)

In order to solve the pre-planning problem for containerships in full routes using an intelligent way, a 0-1 integer programming for the problem is put forward by setting the number of shift and ship longitudinal bending moment value as goals. By the rule based methods, the problem is solved by the Mixed Integer Programming Algorithm (MIPA), Ant Colony Algorithm (ACA) and Genetic Algorithm (GA), respectively. It shows that when the scale of the problem is small, the MIPA is very efficient, and the optimal solution can be found by it. An intelligent algorithm for pre-planning problem of containerships in full routes based on the MIPA, ACA and GA is given, respectively. Finally, the pre-planning result of a containership with 8 bays is shown, it assures that the number of shift is zero, and the ship longitudinal bending moment value is considered as the objective, which means the longitudinal offsets of the center of gravity is minimized.

containerships; pre-stowage; integer programming; Genetic Algorithm; Ant Colony Algorithm

2017-06-15

U695.22

10.3963/j.issn.2095-3844.2017.04.034

汪圓圓(1992—)：男，碩士生，主要研究領域為智能船舶