一種新型ARX模型在三容水箱液位系統中的應用?

劉麗麗左繼紅吳軍鄧秋連

一種新型ARX模型在三容水箱液位系統中的應用?

劉麗麗1，2左繼紅1，2吳軍1鄧秋連1

（1.中南大學信息科學與工程學院長沙410083）（2.湖南鐵道職業技術學院株洲412001）

采用一種新的ARX模型（RBF-ARX模型）對三容水箱液位系統進行建模，闡述了RBF-ARX模型的建模原理、模型結構的確定、模型參數辨識及參數優化等問題。并分析了該模型的優越性能，模型的仿真預測輸出結果，證實了RBF-ARX模型在非線性系統建模和辨識中的可靠性和有效性。

ARX模型；三容水箱系統；非線性系統

Class NumberTP273

1引言

三容水箱液位控制系統屬于工業過程控制中的一種被控對象，具有典型滯后性、非線性和強耦合的特性，其控制模式類似于工業控制中的多種非線性時變多變量耦合系統。其工作過程涉及多個學科，如控制理論、現代控制技術、流體力學等。通過它用戶除可以掌握控制原理、現代控制技術、計算機技術等之外，還可以了解生產工藝流程。因此研究該系統的建模及控制算法問題，對實際工程應用有指導和參考意義［1］。

用經典控制方法對三容水箱液位系統控制時，常因系統的多輸入輸出、非線性和強耦合特性，而使控制變得極為復雜，以致很難達到較為理想的控制效果。針對以上問題，提出了專門針對非線性系統進行建模的新型ARX建模法，采用結構化的離線參數辨識方法得到模型的最優參數，通過實驗驗證該模型的優越性，對控制策略的發揮奠定基礎。

2三容水箱液位系統介紹

實驗用的三容水箱系統由水箱、電控柜、AD/ DA數據采集卡和PC機組成。三容水箱本體結構如圖1所示。

圖1中，水箱本體由蓄水容器、壓力傳感器和動力驅動三大部分構成，動力驅動部分包括水泵、電磁閥以及手動調節閥。水箱和1#、2#、3#水柱用于儲水，水箱為三個水柱提供水源，泵1和泵2分別為1#、3#水柱供水，手動閥LV1，LV5和1#、2#電磁閥控制回路的水流量。每個水柱都安裝了防溢管道，保證了液位到達最高點時經由它流至水箱。3#、4#電磁閥分別是3#、1#水柱的出水閥，手動閥LV2為2#水柱出水閥。3個水柱間安裝LV3、LV4連接閥，可以調節連接閥和出水閥的開度來控制水柱間的耦合和干擾強度，研究表明它是典型的非線性系統。

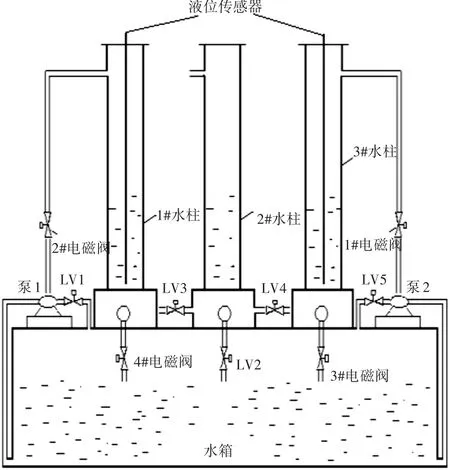
圖1 三容水箱液位控制系統

3 RBF-ARX模型結構及參數辨識

3.1 RBF-ARX模型結構

RBF-ARX模型采用線性自回歸（Auto-Regres?sive eXogenous，ARX）模型［2］和高斯徑向函數（Radi?al Basis Function，RBF）基神經網絡相結合［9～10］，常用于可局部線性化的、時變的多變量非線性系統的建模過程中，采用神經網絡逼近非線性系統模型中依存于狀態的系數，能較好描述系統的全局非線性特性。

針對三容水箱系統，有兩個輸入，分別是u1（1#電磁閥電壓）和u2（2#電磁閥電壓），兩輸出分別是y1（1#水柱水位）和y2（3#水柱水位），其RBF-ARX模型的結構如式（1），如式（1）模型結構采用基本的線性ARX模型，而其模型系數則由高斯徑向基的神經網絡函數逼近［11］，并且是時變的。

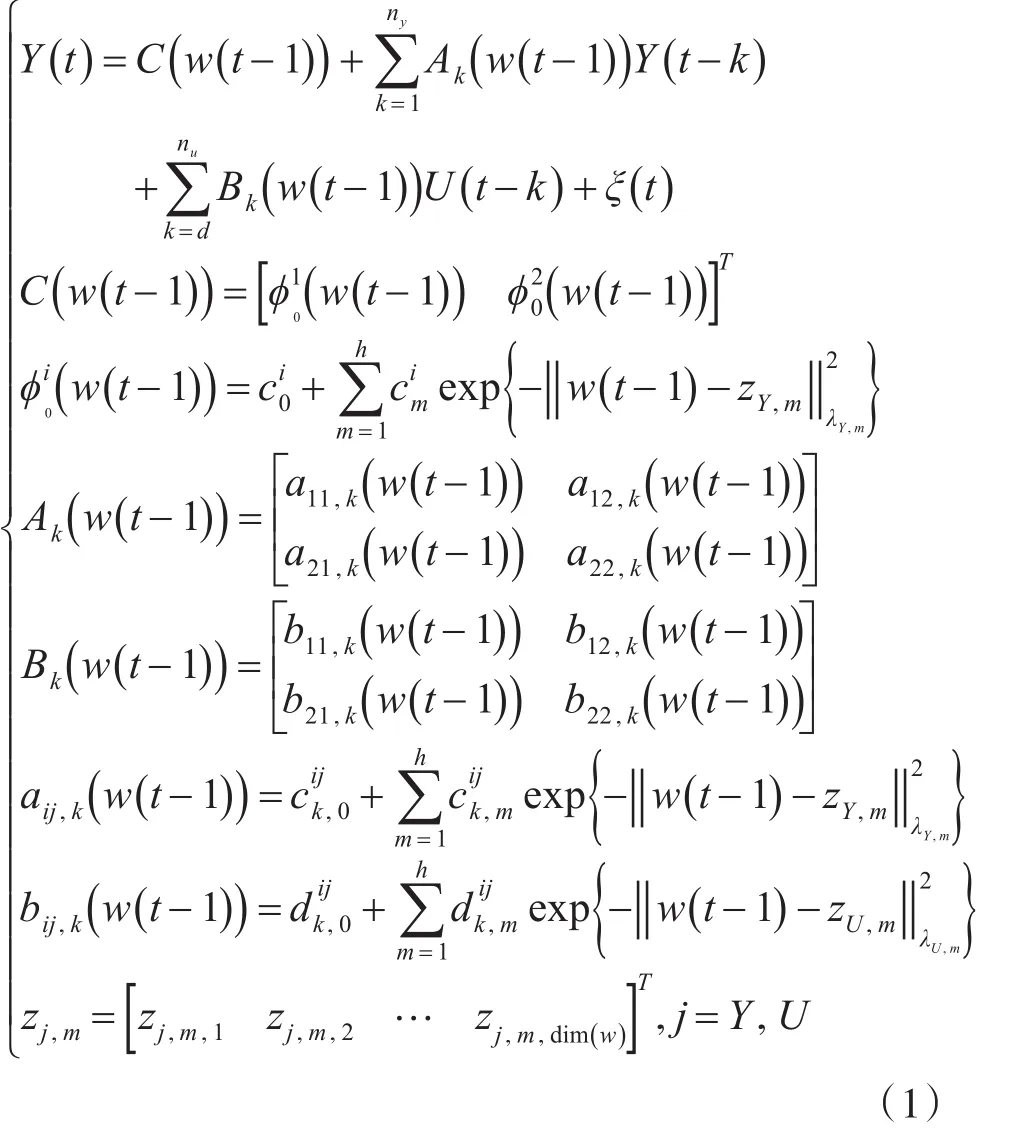
其中，?i0為模型系數，cij，k(i=1，2，…，nj，j=y，u，v; k=0，1，2，…，m)為線性權系數，ny，nu為模型階次，h為非線性環節數目，zj，m為RBF網絡中心，ξ(t)為干擾白噪聲信號，nx=dim{(w(t-1)}為w(t-1)列向量的維數，Y(t)=[y1(t)y2(t)]T∈?是1#和3#水柱水位的輸出矩陣，U(t)=[u1(t)u2(t)]T∈?是1#和2#電磁閥電壓輸入量矩陣，λikj(k=1，2，…，m;i=y，u;j=1，2)為比例系數。

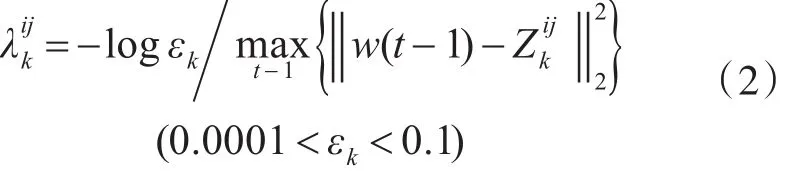
式中，||.||2代表矢量的2-范數。

3.2參數辨識

采用PID算法控制液位在較大范圍內波動，通過改變目標值使輸入輸出在大范圍內波動，并疊加白噪聲信號，使數據體現系統全局動態特性，并采集整個過程輸入輸出數據，用于辨識和檢驗模型。

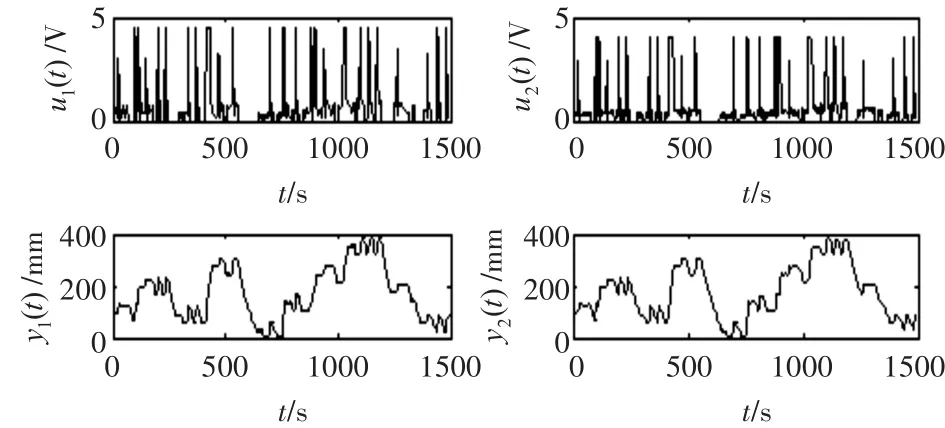
圖2 采集的輸入輸出數據用于辨識模型

RBF-ARX模型的參數可以采用一種快速收斂的結構化非線性參數優化策略來離線估計。它是一種列維布格奈奎爾特方法（Levenberg-Marquardt Method，LMM）［3］和線性最小二乘法（Least Square Method，LSM）［4］相結合的沒有限制的結構化非線性參數優化方法（Structured Nonlinear Parameter Opti?mization Method，SNPOM），這種優化策略是按照如下步驟執行的［5］。

3.2.1參數分類

將模型（1）的參數分成線性參數

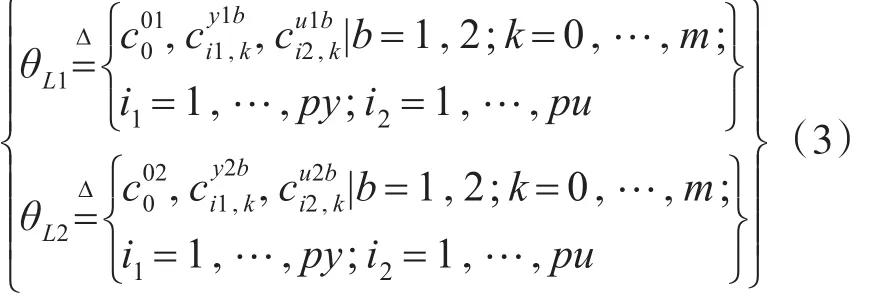
和非線性參數

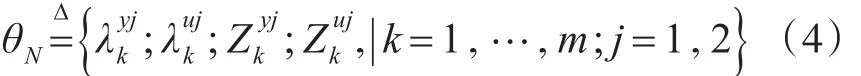
令

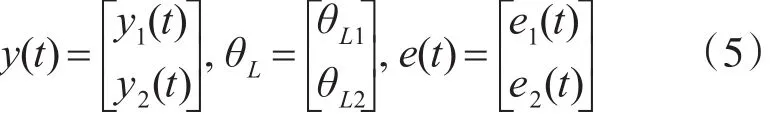
則模型（1）可表示成

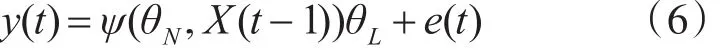
3.2.2選取RBF-ARX模型階次

模型階次包括ny、nu和h，根據經驗h一般選1～2。ny、nu的確定常采用AIC信息準則循環方法［6］，該方法常用于估算相關參數，效果優良，其表達式為

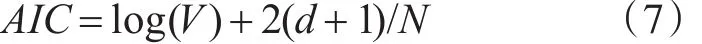
其中，V取誤差標準方差的平方，N為辨識數據長度，d為模型總參數個數，模型（1）中線性參數的個數為(h+1)(2ny+2nu+1)，非線性參數Zki，j，λik，j的個數是8h。綜上總參數d值為

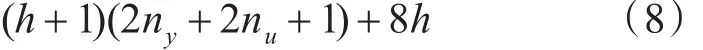
通過采集的輸入、輸出數據（圖2）辨識模型參數，選取m=2，由AIC信息準則計算ny=4，nu=6。

3.2.3 RBF-ARX模型中心變量X(t-1)的選取

模型中X(t-1)的選則非常重要，其選擇與非線性因素息息相關，它可以是輸入矩陣、輸出矩陣或則二者接合。三容水箱的非線性因素與輸入電磁閥電壓與輸出水位有關，故X(t-1)選擇輸入和輸出組合，如下式：

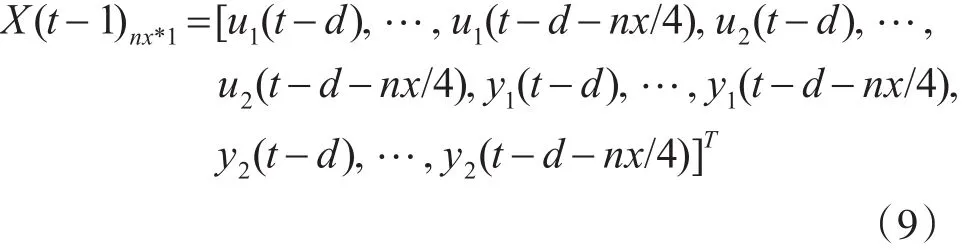
3.2.4模型初始化

確定模型階次后，根據先驗知識確定θN0，采用最小二乘法得出［7］，即

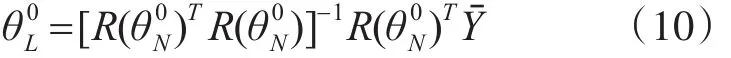
式中

式中，{yˉ1(i)，yˉ2(i)，Xˉ(i-1)|i=τ+1，τ+2，…，M}是辨識數據集合；τ是模型中的最大時間延遲，M是辨識數據長度。[R(θN0)TR(θN0)]-1采用SVD［5］方法以防求逆失敗。

3.2.5優化

目標函數定義如下式［8］：

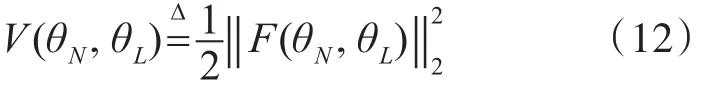
其中，F(θN，θL)表示模型一步向前預測輸出Y^與采樣輸出數據Yˉ的差。

優化問題即求

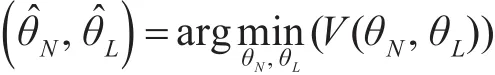
求θkN采用Jacobian矩陣

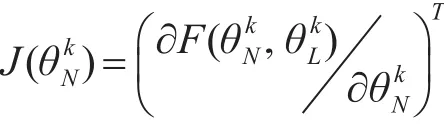
其中k表示重復步數，θkN的遞推如下所示

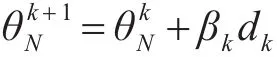
式中，βk是步長，dk是尋優方向，dk根據下式求得

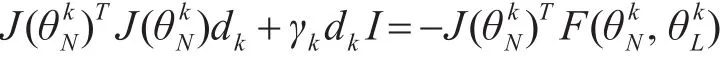
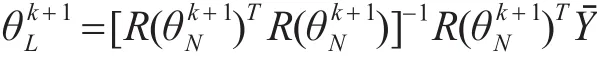
尋優過程就是滿足下式

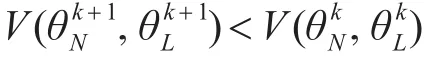
不滿足時，尋優結束。

4模型預測結果分析

通過上面辨識參數步驟，采用圖2采集的輸入輸出數據，辨識并優化RBF-ARX模型參數，非線性參數優化過程如圖3所示，由非線性參數采用最小二乘法可求得模型的線性參數，繼而得到系統的RBF-ARX模型。

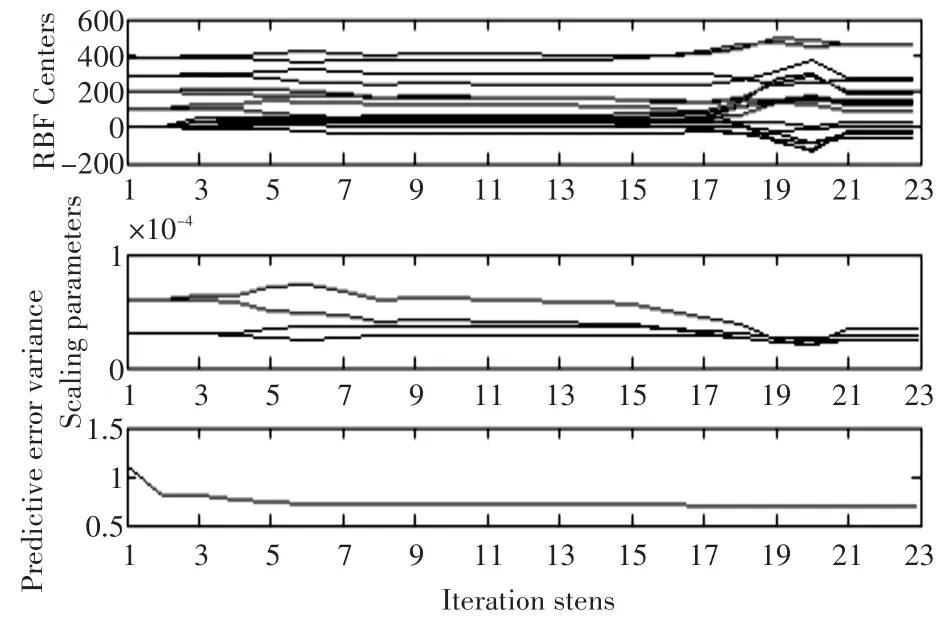
圖3 非線性參數優化過程

從圖3可看出，模型參數的優化過程收斂速度較快，第三個子圖表示輸出向前預測誤差，誤差也比較小。

對辨識出的RBF-ARX模型進行一步預測輸出仿真，如圖4所示。顯然，RBF-ARX模型下系統實際輸出跟蹤期望輸出效果好，誤差波動小且成高斯狀分布，仿真表明建模理想，精度高，能較好反映系統全局非線性特征。

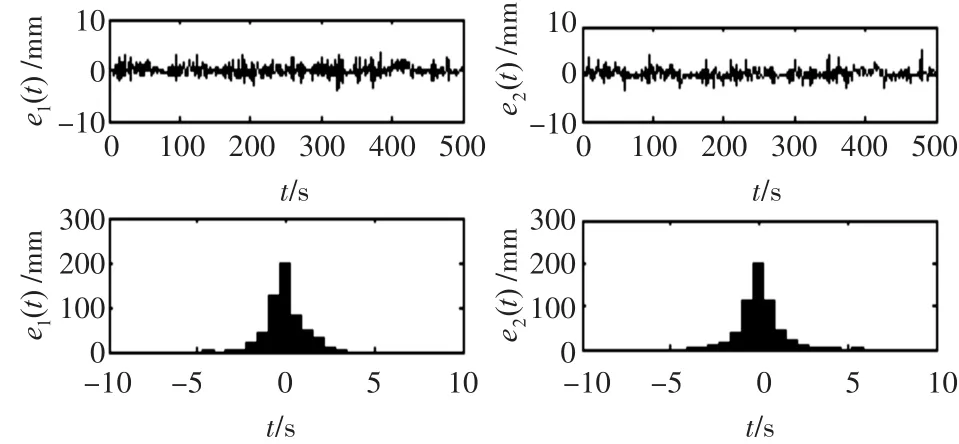
圖4 RBF-ARX模型預測精度

通過觀察模型一步預測誤差相關性函數曲線圖，誤差統計特性類似白噪聲信號。說明RBF-ARX模型能較好描述系統的全局非線性動態特征。

為進一步證明模型精度高，局部放大工作區間內系統實際輸出和模型預測輸出值，觀察誤差情況。圖6和7分別是1#、3#水柱液位模型輸出與實際輸出誤差圖。顯然，系統波動范圍可達400mm，而系統的實際輸出與模型輸出誤差在-5mm～5mm之間波動。系統的模型輸出能較好擬合系統的實際輸出，模型有較好的擬合精度，能準確描述系統的非線性特征。

圖5 模型預測誤差的相關性函數曲線（虛線：e1(t)，實線：e2(t)）

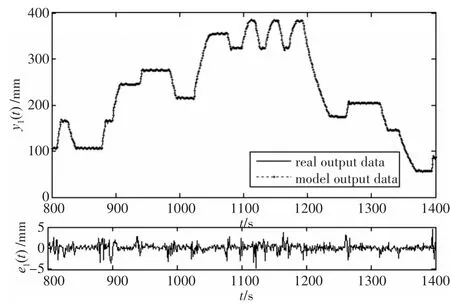
圖6 1#水柱液位RBF-ARX模型輸出與實際輸出對比

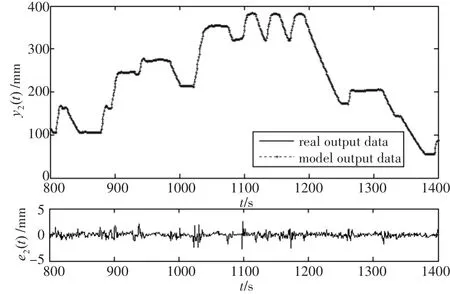
圖7 3#水柱液位RBF-ARX模型輸出與實際輸出

5結語

針對非線性的三容水箱，采取一種RBF-ARX模型對其進行建模。并采用離線的方法辨識參數，通過預測輸出仿真結果分析建模精度，結果表明建模精度高，模型能較好描述系統非線性特性，證實了該建模方法的有效性和優越性。

［1］固高科技.液位過程控制系統實驗指導書［M］.深圳：固高科技，2003：2-20.Solid high-tech.Liquid levelprocess controlsystem exper?imental instruction book［M］.Shenzhen：solid high-tech，2003：2-20.

［2］Hui Peng，Tohru Ozaki，Yukihiro Toyoda，Hideo Shioya，Kazushi Nakano，Valerie Haggan-Ozaki，Massafumi Mo?ri.RBF-ARX model-based nonlinear system modeling and predictive control with application to a Noxdecompo?sition process［J］.Control Engineering Practice，2004，12：191-203.

［3］D.MARQUART，An algorithm for least-squares estima?tion of nonlinear parameter，SIAM J Appl［J］.Math，11（1963）：431-441.

［4］舒迪前.自適應控制［M］.沈陽：東北大學出版社，1993：126-156.

SHU Diqian.Adaptive control［M］.Shenyang：northeast?ern university press，1993：126-156.

［5］徐仲，張凱院，陸全，等.矩陣論簡明教程［M］.北京：科學出版社，2001：145-151.

XU Zhong，ZHANG Kaiyuan，LU Quan，et al.Introductory tutorial matrix theory［M］.Beijing：science press，2001：145-151.

［6］秦宣云，卜英勇，夏毅敏.基于AIC準則優化的徑向神經網絡微地形曲面重構［J］.中南大學學報（自然科學版），2004（10）：815-819.

QIN Xuanyun，BU Yingyong，XIA Yimin.Radial neural network based on AIC criterion optimization tiny terrain surface reconstruction［J］.Journal of central south univer? sity（naturalscience edition），2004（10）：815-819.

［7］蔡自興.智能控制［M］.北京：電子工業出版社，2004：233-235. CAI Zixing.Intelligent control［M］.Beijing：Electronic in?dustry press，2004：233-235.

［8］海山，張策，何風琴.RBF網絡和BP網絡在逼近能力方面的比較研究［J］.內蒙古科技與經濟，2007，14（7）：64-65.

HAIShan，ZHANG Ce，HE Fengqin.RBF network and BP network in approximation ability of comparative study［J］. Science and technology and economy of Inner Mongolia，2007，14（7）：64-65.

［9］張靜.基于RBF網絡的微分先行PID控制器［J］.自動測量與控制，2007，26（9）：60-61.

ZHANG Jing.Derivative ahead of PID controller based on RBF network［J］.Journal of automatic measurement and control，2007，26（9）：60-61.

［10］謝華東，趙陽立，陳志旺.非線性系統的RBF網絡直接廣義預測控制［J］.福建電腦，2007（10）：3-4.

XIE Huadong，ZHAO Yangli，CHEN Zhiwang.RBF net?work direct generalized predictive control of nonlinear systems based on［J］.Journaloffujian，2007（10）：3-4.

［11］孫志兵，戴金海.基于全調節RBF神經網絡的自適應飛行控制器［J］.計算機仿真，2007，24（9）：137-140.

SUN Zhibing，DAIJinhai.Alladjust RBF neuralnetwork based adaptive flight controllers［J］.Computer simula?tion，2007，24（9）：137-140.

Application of A New ARX Modelin Three-tank Water System

LIU Lili1，2ZUO Jihong1，2WU Jun1DENG Qiulian1
（1.Schoolof Information Science and Technology，Central South University，Changsha 410083）（2.Hunan Railway ProfessionalTechnology College，Zhuzhou 412001）

This paper focuses on the modeling of three-tank water system using RBF-ARX model，states the principium of RBF-ARX model，modelstructure confirmation，modelparameters identification，parameter optimization and so on.The superiori?ty of the model is analyzed，the predictive results of simulation show the reliability and effectiveness of RBF-ARX model for the modeling and identification ofnonlinear system.

ARX model，three-tank water system，nonlinear system

TP273

10.3969/j.issn.1672-9722.2017.08.043

2017年2月8日，

2017年3月25日

2015年度國家自然科學基金：抗參數橫揺的欠驅動船舶航跡跟蹤控制研究（編號：61403045）；2015年度湖南省教育廳科學研究資助項目：四旋翼飛行器的建模及控制策略的研究（編號：15C0903）資助。

劉麗麗，女，碩士研究生，講師，研究方向：復雜非線性系統建模及控制方法。左繼紅，男，碩士研究生，講師，研究方向：復雜非線性系統建模及控制方法。吳軍，男，博士，講師，研究方向：復雜非線性系統建模及控制方法。鄧秋連，女，碩士，高級工程師，研究方向：復雜非線性系統建模及控制方法。