基于AFM膠體探針測量液固界面DLVO力及表面電勢

田維芳, 鄭 旭, 李戰華, 徐 征

(1. 大連理工大學 機械工程學院, 遼寧 大連 116024; 2. 中國科學院力學研究所 非線性力學國家重點實驗室, 北京 100190)

基于AFM膠體探針測量液固界面DLVO力及表面電勢

田維芳1, 鄭 旭2,*, 李戰華2, 徐 征1

(1. 大連理工大學 機械工程學院, 遼寧 大連 116024; 2. 中國科學院力學研究所 非線性力學國家重點實驗室, 北京 100190)

表面電勢是微納流控芯片中流體流動的重要參數。本文介紹了基于AFM膠體探針技術測量液固界面DLVO力并進一步測量表面電勢及表面電荷密度的方法。本文改進了膠體探針制作的技術手段，并提出用雙探針法測量膠體探針的彈性系數。在0.1～1mM濃度范圍內的NaCl溶液中，測量了硅、二氧化硅和氮化硅液固界面雙電層內的DLVO力及表面電勢。實驗結果表明膠體探針技術可以很好地測量液固界面的DLVO力，尤其對靜電力指數變化段非常敏感。通過DLVO力曲線可以間接測量表面電勢、表面電荷密度等重要參數，是微納流動及界面屬性測量的有效手段。此外，在不同硅基材料表面的測量結果顯示了硅烷醇基密度對表面電勢起主導作用，可以通過選用不同硅烷醇基密度的材料來有效調控表面電勢，從而在硅基材料制作的微流控芯片中調控電動流動的強弱。

AFM；膠體探針；液固界面；DLVO力；表面電勢

0 引 言

水和氣體、固體間的界面問題無處不在，且在生活及大多數工業領域都十分重要[1]。近年來隨著流動尺度的進一步減小，納流控應運而生，在生物芯片技術、新能源領域及微納尺度化學分析等方面都有廣闊的應用前景[2]。溶液中，固體表面會從溶液中選擇性地吸附離子或是固體表面的帶電基團解離而帶電。根據電中性原理，帶電表面附近的液體中必有與固體表面電荷數量相等但符號相反的反離子，帶電表面和反離子構成雙電層。由于電荷分離而造成的液固兩相內部的電位差稱為表面電勢。表面電荷/表面電勢引起的雙電層會對微納米尺度的流體流動產生重要影響[1,3]。因此精確測量雙電層內表面電勢/表面電荷密度，進而有效調控表面電勢/表面電荷密度顯得尤為重要。

傳統測量液固界面表面電勢及表面電荷密度的方法有流動電位法及電滲法[4-5]。Kirby[4]等人通過流動電位法間接測量了硅基表面的zeta電勢。在外力驅動下，微通道中液體流動帶動帶電離子沿流動方向運動，使電荷在下游沉積，產生電位差，即流動電位，從而通過計算得到zeta電勢。電滲法則是通過測量電滲流速度間接測量zeta電勢。這2種方法都是測量雙電層中的擴散層自由電荷相對液固界面的輸運，其界面電勢是基于剪切滑移面定義的，即zeta電勢。DLVO理論[1]描述了液固界面帶電表面相互作用力，包括范德華力和靜電力。而由靜電排斥定義的表面電勢直接基于液固界面，不受滑移面位置的影響，是更能代表液固界面的本征屬性[1,6-7]。基于DLVO理論，本文改進了AFM膠體探針測量表面電勢ψ的方法。考慮到近年來硅基材料在MEMS傳感器上的廣泛應用[8]，測量硅基材料液固界面作用力、表面電勢以及表面電荷密度對MEMS傳感器的研究有著重要的實踐意義，同時也是實驗流體測量技術在微納尺度的重要發展。

1 實驗部分

1.1 實驗測量方法

本實驗基于原子力顯微鏡膠體探針技術測量表面電勢，儀器采用Asylum Research 公司的MFP-3DTM原子力顯微鏡。圖1為AFM液下工作原理示意圖。膠體探針由膠體球和無針尖懸臂梁粘結，在實驗室自行加工而成(詳見下文1.2節)。膠體探針由壓電控制器控制以恒定速度接近樣品表面，過程中受到靜電力、水動力學阻力及范德華力作用，這些力的綜合作用使得懸臂梁(Cantilever)產生微小變形。所以當激光(Laser)照射到懸臂梁末端時，其反射光的位置也會發生變化，造成偏移量的產生，懸臂梁的變形可由偏移量在光電位置敏感器件(Position sensitive detector)上的反饋得到。基于胡克定律，通過變形量及懸臂梁彈性系數可測得力。圖1中，Zs為系統基準位置位移，向上為正方向，由AFM中壓電傳感器測量得出；drect為膠體探針彈性變形，大小可由前述激光反射位移偏移量決定；D由Zs和drect計算得到。基于此測試系統，由Igor Pro軟件可直接得膠體探針表面到基底之間距離D與膠體探針所受DLVO力和水動力學阻力關系曲線。在無滑移邊界條件下的牛頓流體中，球面接近平面過程中所受水動力學阻力可由公式(1)描述[9]：

式中：η為水動力學粘滯系數；r為球半徑；U為接近速度；h為球面與平面距離。所以，液體環境下，當膠體探針(直徑為20.0±0.5μm)以極低的速度(10nm/s量級)接近樣品底面時，在距離壁面10nm左右位置，水動力學阻力最大只有約10-11N，而本實驗關注的DLVO力量級在10-9N量級，相比之下水動力學阻力可忽略不計，本實驗只考慮靜電力與范德華力。

1.2 AFM膠體探針制作及其彈性系數測量

實驗采用直徑為20.0±0.5μm的二氧化硅小球(Duke Scientific，此種微球表面粗糙度最小[10])。取適量小球顆粒放到燒杯中，加入無水乙醇，超聲清洗5min，重復此步驟2次。清洗完成后用普通標準探針(Asylum Research)掃描小球工作區域形貌，表面RMS均方根粗糙度在1nm以下(掃描范圍5μm×5μm)，如圖2所示。

超純水超聲清洗蓋玻片30h，烘干備用。AFM膠體探針具體制作步驟如圖3所示：使用移液器量取100μL清洗后小球與乙醇混合液滴在干凈的蓋玻片上，烘干晾至室溫，如圖3(1)和(2)所示；然后將混合均勻的環氧樹脂AB膠粘取針尖大小到蓋玻片上。將此蓋玻片放到實驗平臺上，利用AFM測試系統使無針尖懸臂梁(Nano Sensors，彈性系數0.12N/m，厚2.0±1μm，長450±10μm,寬50±7.5μm)接近膠水表面，黏著少量膠水，如圖3(3)和(4)所示；然后上移無針尖懸臂梁，左右移動測試系統水平XY調節平臺，找到合適的二氧化硅小球。慢慢使無針尖懸臂梁下降，同時左右移動測試系統XY調節平臺，使小球正對懸臂梁下方，懸臂梁下降至接觸到小球為止，等待1min左右，上移懸臂梁，等待膠水完全凝結，此時膠體探針制作完成，如圖3(5)和(6)所示。

探針彈性系數的測量方法有幾何法[11]、熱噪聲法[12]、水動力學法[13-14]和附加質量法[15]等，本實驗采用系統自帶熱噪聲法標定普通探針彈性系數。實驗所用普通探針為Bruker公司的探針，熱噪聲法測得彈性系數為krect=0.15N/m (誤差在4%內)。因膠體探針上小球質量比懸臂梁大得多，故不能使用熱噪聲法測膠體探針彈性系數。本實驗欲采用雙探針法測膠體探針彈性系數，即用普通探針壓迫膠體探針使其形變，測量原理如圖4所示。將膠體探針固定到蓋玻片上，普通探針安裝在AFM上，普通探針下壓膠體探針過程中，2探針產生形變，設變形量分別為drect、dprobe，彈性系數分別為krect、kprobe，彈性力為F。2個探針的受力變形過程可看作是2彈性體的串聯，則總彈性系數為k=krect×kprobe/(krect+kprobe)，總變形量為d=drect+dprobe。由AFM測試系統可得F與d關系曲線，斜率的絕對值即為k，此時可得到kprobe=krect×k/(k-krect)。實驗測得自行粘結膠體探針彈性系數為0.27±0.05N/m。本實驗用此雙探針法實際測量了膠體探針的彈性系數，比僅僅通過幾何法或熱噪聲法得到的簡單估算值更加可靠。由于2探針受力過程可相當于一個兩彈簧串聯模型，一般認為2探針變形量越接近則測得的彈性系數越接近真值，且不易因探針懸臂梁彎曲過大而受損壞。本實驗結果也表明當用來標定的標準探針彈性系數接近膠體探針彈性系數時測量結果的重復性較好。

Fig.4 Schematic of measuring colloidal probe spring constant based on cantilever to cantilever device

1.3 表面電勢測量方法

AFM膠體探針是通過測量膠體探針受到帶電表面的作用力來測量表面電勢及表面電荷密度的。基于DLVO 理論，膠體探針與表面之間的相互作用力為范德華力和靜電力之和，其相互作用能表達式為：

WDLVO(D)=

(2)式右側第一項表示靜電力的作用能，第二項表示范德華力作用能。基于Derjaguin近似，相互作用力為[1,6-7]：

由公式(2)、(3)得：

(4)式中，ε為介電常數，к-1為德拜(Debye)長度，ψ1為探針表面電勢，ψ2為基底表面電勢，D為探針與壁面接觸面距壁面距離，R為探針球半徑，A為Hamaker常數，取1.2×1020J。此處含有3個未知數；к-1、ψ1和ψ2，由公式(4)可知，表面電勢ψ1和ψ2由靜電力部分決定。一般認為，靜電力主導的作用范圍在距離壁面2к-1～3к-1的范圍內，因此，對此范圍的力曲線進行線性擬合即可得德拜(Debye)長度 к-1的倒數к。理論上，如果確定了ψ1，就可以通過力曲線擬合唯一確定待測表面電勢ψ2。因此，表面電勢ψ2的確定需要2步：(1) 對稱結構測探針表面電勢ψ1。選用和探針材質相同的SiO2作基底，即SiO2-SiO2，此時，ψ1=ψ2。通過AFM測試系統可得DLVO力與距離D關系，將此實驗數據與公式(4)中理論曲線在2к-1～3к-1范圍內擬合得探針表面電勢ψ1；(2) 非對稱結構測基底表面電勢，例如選用氮化硅表面做基底，即SiO2-Si3N4。將第(1)步中得到的探針表面電勢ψ1代入公式(4)，此時只剩一個未知數ψ2。采用同樣的方法，將在氮化硅表面所測實驗數據與理論力曲線擬合可得氮化硅表面電勢ψ2。

此法也為測量表面電荷密度提供新思路。擴散層中，由Grahame 方程可得表面電荷密度與表面電勢關系，

式中：ε為介電常數；kB為玻爾茲曼常數；T為溫度；e為電子數。基于電中性原理，液固界面的表面電荷密度應與擴散層中的反電荷中和。因此，一定液體環境下，已知表面電勢就可以唯一確定表面電荷密度。

1.4 基底制備

等離子體輔助化學氣相沉積(Plasma Enhanced Chemical Vapor Deposition，PECVD)屬于化學氣相沉積的一種類型，主要是借助施加一個射頻功率產生輝光放電等離子體，使反應氣體發生化學反應形成介質薄膜的技術。

本實驗采用此技術制備氮化硅和二氧化硅薄膜，步驟如下：(1) 取直徑大小為2inch，厚500μm<100>的單面拋光硅片若干片，放入體積比為濃H2SO4∶H2O2= 7∶3的混合溶液中，在80℃水浴下加熱30min，然后用去離子水清洗，并用烘箱烘干備用；(2) 采用OXFORD-NGP80 DEP薄膜沉積設備，在烘干后的硅片上單面沉積氮化硅薄膜。采用同樣的步驟制備二氧化硅薄膜。然后用光譜橢偏儀分別測得沉積氮化硅薄膜厚度為53.4±0.1nm，二氧化硅薄膜厚度為48.5±0.1nm。 AFM掃描清洗后硅片表面形貌得表面RMS均方根粗糙度均為1nm以下(掃描范圍5μm×5μm)。氮化硅和二氧化硅薄膜表面RMS均方根粗糙度均為2nm以下(掃描范圍5μm×5μm)。

2 結果與討論

首先，對稱結構SiO2-SiO2確定探針表面電勢。本實驗采用超純水與分析純氯化鈉配制0.1、0.3、0.8和1 mM 4種不同濃度氯化鈉溶液。電導率儀測得溶液pH為5.5左右，電導率分別為11.2、35.4、60.0和115.2μs/cm，通過電導率與濃度關系計算得溶液實際濃度分別為0.09、0.28、0.48和0.93mM。德拜(Debye)長度可由下式近似計算，

式中：c為溶液濃度(mol/L)，κ-1為德拜(Debye)長度(nm)。表1所示為電導率儀(METTLER TOLEDO，SevenMulti S40)測得上述4種濃度溶液的電導率、實際濃度、德拜(Debye)長度理論值及德拜(Debye)長度實驗值對應關系。

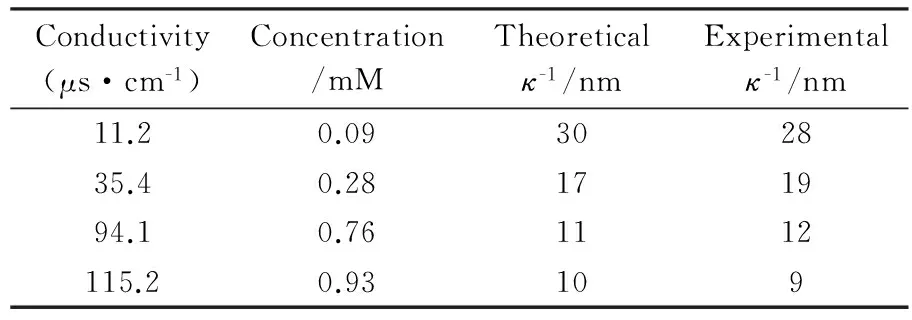
表1 不同氯化鈉濃度下的電導率與德拜長度對照表Table 1 Conductivity and Debye length in different NaCl solutions

AFM接近基底表面過程中主要受靜電排斥力和范德華吸引力，將當靜電排斥力不足以抵抗范德華吸引力時引起的探針跳變點處作為壁面，也就是距離零點。AFM測得DLVO力曲線如圖5所示：膠體探針距壁面D>100nm時DLVO力主要為0.01～0.1nN的噪音；逐漸靠近壁面，在1.5к-1～3к-1范圍內主要是靜電力起作用，且以指數衰減；當靠近到距壁面10nm時，范德華力開始顯現，隨著到壁面距離的進一步減小，影響逐漸明顯。在1κ-1范圍內，對0.09mM濃度的溶液，DLVO力在6～10nN之間，而0.93mM的在2～5nN之間，主要是因為表面電勢及表面電荷密度隨著溶液濃度的增大而減小，導致靜電排斥力減小。表面電勢的求解主要由1.5κ-1～ 3κ-1范圍決定，由圖可知此范圍內實驗數據與理論值擬合較好，也與Ducker[17]及Horn[18]等人的實驗結果一致性較好。從圖中還可明顯看出，DLVO理論擬合曲線在距離壁面1.5κ-1內與實驗曲線相比存在一定偏差，此現象在前人實驗中也被發現[16]。原因主要是公式(3)中靜電力的理論值是基于Poisson-Boltzmann 方程的線性解，會在距離壁面較近的位置存在一定的偏差；同時，在大表面電勢的稀濃度溶液中該偏差也明顯更大。

圖5 二氧化硅基底上膠體探針在4種不同濃度氯化鈉溶液下的對數坐標力曲線，黑線為連續電勢假設下的PB方程擬合線

Fig.5 Force curves between the colloidal probe and silica in different NaCl concentrations. The black curves are fitted based on PB equation under the assumption of constant potential

圖6所示為膠體探針表面電勢與溶液濃度關系。由圖可知，表面電勢ψ與pC呈線性關系ψ=-28.98×pC+55.21，與Kirby[4]給出的線性理論相近(pC=-log10C,C為濃度)。本實驗在與Ducker[17]及Horn[18]相似的實驗條件下，結果與其也較為接近。二氧化硅表面電荷主要是由硅烷醇基電離產生的負電荷，吸附溶液中的陽離子(氫離子和鈉離子)，中和部分表面電荷，液相剩余的凈電荷與固相形成電位差，即表面電勢。體溶液中的電勢為零電勢點，那么樣品表面電勢為負值。因此，隨著溶液濃度的增加(對應pC減小)，表面電勢絕對值減小。表面電勢測量誤差通常在±5～10mV以內，一般認為是由膠體探針表面及基底表面粗糙度、膠體探針彈性系數標定誤差及AFM系統誤差及外界噪聲干擾等因素造成。

圖6 二氧化硅表面電勢測量結果(紅點)及與Ducker(圓圈)和Horn(矩形)在相似測量環境下的結果比較。pC=-lgC(C為溶液濃度)

Fig.6 Comparison of the surface potential on silica (red symbols) between Duckers’ (circles) and Horns’ (squares) under similar experiment conditions.pC=-lgC.(Cis concentration)

圖7所示為硅、二氧化硅及氮化硅表面電勢對比圖。一般認為，由于硅表面易被氧化，硅與二氧化硅液固表面都是同樣排布的硅烷醇基。因此，實驗測得硅和二氧化硅在氯化鈉溶液中表面電勢及表面電荷密度相同。而氮化硅表面電勢絕對值比硅和二氧化硅的小10～20mV左右。推測其原因為：硅基樣品表面電荷主要是由于硅烷醇基的電離產生。單位面積內氮化硅表面所帶硅烷醇基比二氧化硅少[19]，濃度等環境一致的條件下，氮化硅表面比二氧化硅表面剩余凈電荷少，因此，表面電勢絕對值也較小。

Fig.7 Comparison of surface potentials on silicon, silica and silicon nitride

3 結 論

本文詳細介紹了膠體探針的制作過程及其彈性系數標定方法，通過AFM膠體探針測量系統測量了不同硅基表面液固界面的DLVO力，從而間接測量了表面電勢及表面電荷密度，主要結論如下：

(1) AFM膠體探針技術可以很好地測量出靜電力的指數衰減段，并可以單獨由此段力曲線確定德拜 長度，表征靜電作用的特征。通過DLVO理論擬合實驗曲線可以得到表面電勢，表面電荷密度等重要參數。考慮到PB方程的適用性以及靜電作用主導的強弱，0.1～1mM濃度是該技術的最優測量范圍。

(2) 硅和二氧化硅在條件相同下表面電勢絕對值較為接近，而氮化硅要小10～20mV，原因主要是單位面積內氮化硅表面所帶硅烷醇基比二氧化硅少，導致在濃度等環境一致的條件下氮化硅表面比二氧化硅表面剩余電荷少，因此，表面電勢絕對值也較小。此結果表明，可以通過選取不同硅烷醇基密度的材料來有效調控表面電勢，從而在硅基材料的微流控芯片中調控電動流動的強弱。

[1]Israelachvili J N. Intermolecular and surface forces[M]. Academic Press, 2011.

[2]李戰華, 吳健康, 胡國慶等. 微流控芯片中的流體流動[M]. 北京: 科學出版社, 2012.

Li Z H, Wu J K, Hu G Q, et al. Fluid flow in microfluidic chips[M]. Beijing: Science Press, 2012.

[3]林炳承, 秦建華. 圖解微流控芯片實驗室[M]. 北京: 科學出版社, 2008.

Lin B C, Qin J H. Graphic laboratory on a microfluidic chip[M]. Beijing: Science Press, 2008.

[4]Kirby B J, Hasselbrink E F. Zeta potential of microfluidic substrates: Theory, experimental techniques, and effects on separations[J]. Electrophoresis, 2004, 25(2): 187-202.

[5]Schoch R, Han J, Renaud P. Transport phenomena in nanofluidics[J]. Review of Modern Physics, 2008, 80(3): 839-883.

[6]Butt H J, Cappella B, Kappl M. Force measurements with the atomic force microscope: technique, interpretation and applications[J]. Surface Science Reports, 2005, 59(1-6): 1-152.

[7]Audry M C, Piednoir A, Joseph P, et al. Amplification of electro-osmotic flows by wall slippage: direct measurements on OTS surfaces[J]. Faraday Discussions, 2010, 146(146): 113-124.

[8]郝旭歡, 常博, 郝旭麗. MEMS傳感器的發展現狀及應用綜述[J]. 無線互聯科技, 2016, 3: 95-96.

Hao X H, Chang B, Hao X L. Current development and application of MEMS sensors[J]. Wireless Internet Technology, 2016, 3: 95-96.

[9]Horn R G, Vinogradova O I, Mackay M E, et al. Hydrodynamic slippage inferred from thin film drainage measurements in a solution of nonadsorbing polymer[J]. Journal of Chemical Physics, 2000, 112(14): 6424-6433.

[10]Van Zwol P J, Palasantzas G, Van de Schootbrugge M, et al. Roughness of microspheres for force measurements[J]. Langmuir, 2008, 24(14): 7528-7531.

[11]Sader J E, Larson I, Mulvaney P, et al. Method for the calibration of atomic force microscope cantilevers[J]. Review of Scientific Instruments, 1995, 66(7): 3789-3798.

[12]Butt H J, Jaschke M. Calculation of thermal noise in atomic force microscopy[J]. Nanotechnology, 1995, 6(1): 1-7.

[13]Sader J E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope[J]. Journal of Applied Physics, 1998, 84(1): 64-76.

[14]Sader J E, Chon J W M, Mulvaney P. Calibration of rectangular atomic force microscope cantilevers[J]. Review of Scientific Instruments, 1999, 70(10): 3967-3969.

[15]Cleveland J P, Manne S, Bocek S, et al. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy[J]. Review of Scientific Instruments, 1993, 64(2): 403-405.

[16]Kuznetsov V, Papastavrou G. Ion adsorption on modified electrodes as determined by direct force measurements under potentiostatic control[J]. The Journal of Chemical Physics C, 2014, 118 (5): 2673-2685.

[17]Ducker W A, Senden T J, Pashley R M. Direct measurement of colloidal forces using an atomic force microscope[J]. Nature, 1991, 353(353): 239-241.

[18]Horn R G, Smith D T. Measuring surface forces to explore surface chemistry: Mica, sapphire and silica[J]. Journal of Non-Crystalline Solids, 1990, 120(1-3): 72-81.

[19]Legrand P A. The surface properties of silicas[J]. International Journal of Food Science & Technology, 2015, 50(4): 966-973.

(編輯：楊 娟)

Measuring DLVO force and surface potential based on AFM colloidal probe technique at liquid-solid interfaces

Tian Weifang1, Zheng Xu2,*, Li Zhanhua2, Xu Zheng1

(1. School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China; 2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China)

Surface potential is an important parameter of the fluid flow in microfluidics. This study develops a method to measure the surface potential and surface charge density based on the DLVO force obtained by colloidal probe technique using atomic force microscope (AFM). A novel procedure of colloidal probe fabrication is proposed, and then a cantilever-to-cantilever calibration method is used to determine the spring constant of the colloidal probe. We thus measure DLVO forces and surface potentials of silicon, silica and silicon nitride substrates, in 0.1 mM to 1 mM NaCl solutions respectively. The results show that our approach could well measure the DLVO forces at the liquid-solid interfaces, which is especially sensitive to the exponential variation of the electrostatic force. The surface potential, the surface charge density and other important parameters can be obtained via fitting the force curves. Additionally, the variation of surface potentials at different silicon-based surfaces indicates that the density of silane groups plays a dominant role on the surface potential. Thus it is possible to effectively control the surface potential by changing the silane density of the silicon-based materials. The findings could be valuable to regulating electro kinetic flow intensity in microfluidic chips.

AFM;colloidal probe;liquid-solid interfaces;DLVO force;surface potential

1672-9897(2017)04-0016-06

10.11729/syltlx20160163

2016-10-31;

2017-01-09

自然科學基金項目(11202219);遼寧省教育廳重點實驗室基礎研究項目(LZ2014005)

TianWF,ZhengX,LiZH,etal.MeasuringDLVOforceandsurfacepotentialbasedonAFMcolloidalprobetechniqueatliquid-solidinterfaces.JournalofExperimentsinFluidMechanics, 2017, 31(4): 16-21. 田維芳, 鄭 旭, 李戰華, 等. 基于AFM膠體探針測量液固界面DLVO力及表面電勢. 實驗流體力學, 2017, 31(4): 16-21.

O363.2；O363.9

A

田維芳(1993-)，女，河南新鄉人，碩士研究生。研究方向：液固界面雙電層內表面電勢測量及調制研究。通信地址：遼寧省大連市甘井子區凌工路2號大連理工大學機械東樓(116024)。E-mail：tianweifang1993@163.com

*通信作者 E-mail: zhengxu@lnm.imech.ac.cn