CONVERGENCE THEORY ON QUASI-PROBABILITY MEASURE
ZHANG Chun-qin,ZHANG Hui
(College of Mathematics and Information Science,Hebei University,Baoding 071002,China)
CONVERGENCE THEORY ON QUASI-PROBABILITY MEASURE
ZHANG Chun-qin,ZHANG Hui
(College of Mathematics and Information Science,Hebei University,Baoding 071002,China)
In this paper,we investigate the relationships among the convergence concepts on quasi-probability space.By using analogy method,some new convergence concepts for quasirandom variables are proposed on quasi-probability space and the relationships among the convergence concepts are discussed.Convergence theory about fuzzy measure is obtained,and all conclusions are natural extensions of the classical convergence concepts to the case where the measure tool is fuzzy.
quasi-probability measure;convergence theory;convergence concept;quasirandom variables
1 Introduction
Convergence theory was well developed based on classical measure theory,and some applications can be found in[1-3].As for convergence theory in fuzzy environments,information and data are usually vague or imprecise which is essentially dif f erent from the classical measure case[4-6].Therefore,it is more reasonable to utilize quasi-probability measure,which is an important extension of probability measure[1-2]to deal with fuzziness,to study such convergence theory.Quasi-probability measure was introduced by Wang [6],which of f ered an efficient tool to deal with fuzzy information fusion,subjective judgement,decision making,and so forth[7-11].
Convergence concepts play an important role in classical measure theory.Some mathematics workers explored them for fuzzy(or non-additive)measures such as Liu[12-13], Wang[14],Zhang[4-5],Gianluca[15],and so on.While the measure tool is non-additive, the convergence concepts are very dif f erent from additive case.In order to investigate quasiprobability theory deeper,we will propose in the present paper some new convergence concepts on quasi-probability space,and discuss the relationships among the convergence con-cepts.Our work helps to build important theoretical foundations for the development of quasi-probability measure theory.
The paper is outlined as follows:Section 1 is for introduction.In Section 2,some preliminaries are given.In Section 3,we study convergence concepts of q-random variables sequence and,ultimately,Section 4 is for conclusions.
2 Quasi-Probability Measure
In this paper,let X be a nonempty set and(X,F)be a measurable space,here F is a σ-algebra of X.If A,B∈F,then the notation A?B means that A is a subset of B,and the complement of A is denoted by Ac.
Def i nition 2.1[6]Let a∈(0,+∞],an extended real function is called a T-function if f θ:[0,a]→[0,+∞]is continuous,strictly increasing,and such that θ(0)=0,θ-1({∞})=?or{∞},according to a being f i nite or not.
Let a∈(0,+∞],an extended real function θ:[0,a]→[0,+∞]is called a regular function,if θ is continuous,strictly increasing,and θ(0)=0,θ(1)=1[10].
Obviously,if θ is a regular function,then θ-1is also a regular function.
Def i nition 2.2[6]μis called quasi-additive if fthere exists a T-function θ,whose domain of def i nition contains the range ofμ,such that the set function θ?μdef i ned on F by(θ?μ)(E)=θ[μ(E)](?E∈F),is additive;μis called a quasi-measure if fthere exists a T-function θ such that θ?μis a classical measure on F.The T-function θ is called the proper T-function ofμ.
Def i nition 2.3If θ is a regular T-function ofμ,thenμis called a quasi-probability. The triplet(X,F,μ)is called a quasi-probability space.
From Def i nition 2.3,we know probability is a quasi-probability with θ(x)=x as its T-function.
Example 2.1Suppose that X={1,2,···,n},ρ(X)is the power set of X.If
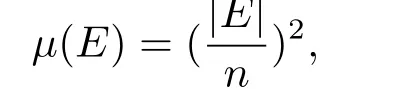
De fi nition 2.4Let(X,F,μ)be a quasi-probability space,and ξ=ξ(ω),ω∈X,be a real set function on X.For any given real number x,if{ω|ξ(ω)≤x}∈F,then ξ is called a quasi-random variable,denoted by q-random variable.The distribution function of q-random variable ξ is de fi ned by Fμ(x)=μ{ω∈X|ξ(ω)≤x}.
Let ξ and η be two q-random variables.For any given real numbers x,y,if
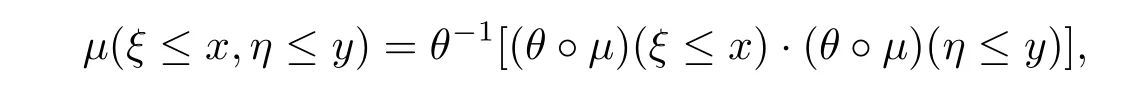
Theorem 2.1 Letμbe a quasi-probability on F.Then there exists a regular T-function θ,such that θ?μis a probability on F[4].
Theorem 2.2Ifμis a quasi-probability,thenμis continuous andμ(?)=0[4].
Theorem 2.3Letμbe a quasi-probability on F,A,B∈F,then we have
(1)if A?B,thenμ(A)<μ(B);
(2)ifμ(A)=0,thenμ(Ac)=1;
(3)μ(A∪B)≤θ-1[(θ?μ)(A)+(θ?μ)(B)].
Proof(1)Since A?B,and there exists a T-function θ such that θ?μis a probability, we have(θ?μ)(A)<(θ?μ)(B),θ is continuous,strictly increasing,it is clear thatμ(A)<μ(B).
(2)Since θ?μis a probability,one can have

which implies that
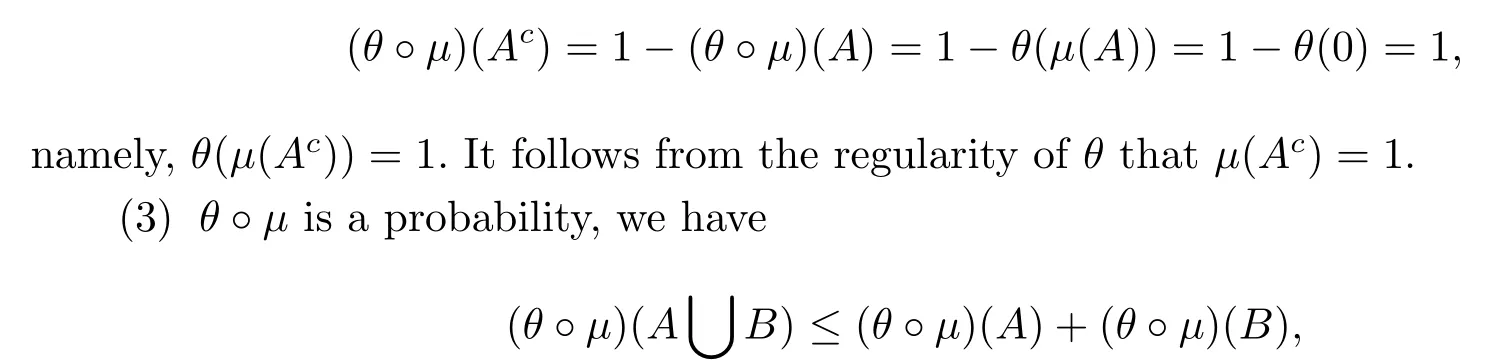
that is,
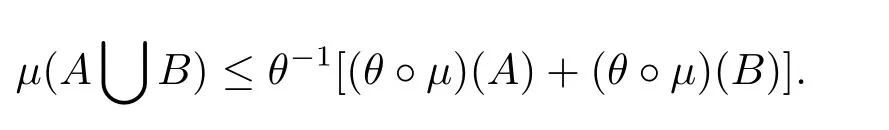
3 Convergence Concepts of q-Random Variables Sequence
In the section,we introduce some new convergence concepts such as convergence almost surely,convergence in distribution,fundamental convergence almost everywhere,fundamental convergence in quasi-probability,etc.,and we will investigate the relationships among the convergence concepts.
Def i nition 3.1[4]Suppose that ξ,ξ1,ξ2,···,ξn,···are q-random variables def i ned on the quasi-probability space(X,F,μ).If
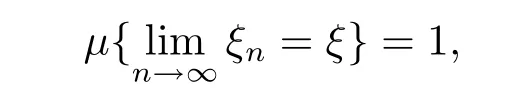
then we say that{ξn}converges almost surely to ξ.Denoted by
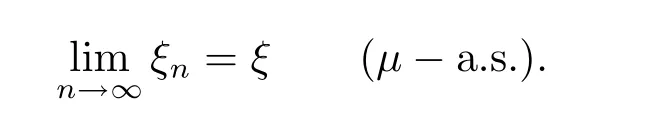
Def i nition 3.2Suppose that ξ,ξ1,ξ2,···,ξn,···are q-random variables def i ned on the quasi-probability space(X,F,μ).If there exists E∈F withμ(E)=0 such that{ξn} converges to ξ on Ec,then we say{ξn}converges to ξ almost everywhere.Denoted by
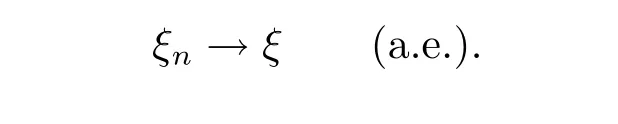
Def i nition 3.3Suppose that ξ1,ξ2,···,ξn,···are q-random variables def i ned on the quasi-probability space(X,F,μ).If there exists E∈F withμ(E)=0 such that for any x∈Ec,
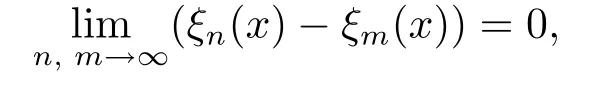
then we say{ξn}is fundamentally convergent almost everywhere.
Def i nition 3.4[4]Suppose that ξ1,ξ2,···,ξn,···is a sequence of q-random variables. If there exists a q-random variable ξ,such that?ε>0,
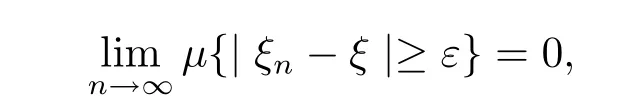
namely,
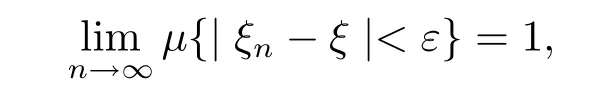
then we say that{ξn}converges in quasi-probability to ξ.Denoted by
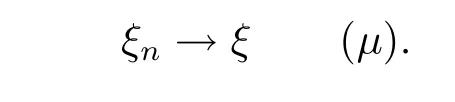
Def i nition 3.5Suppose that ξ1,ξ2,···,ξn,···are q-random variables.If for any given ε>0,
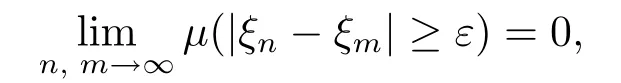
then we say{ξn}fundamentally converges in quasi-probability.
Def i nition 3.6Suppose that Fμ(x),F1μ(x)F2μ(x)···are the distribution functions of q-random variables ξ,ξ1,ξ2,···,respectively.The sequence{ξn}is said to be convergent in distribution to ξ if
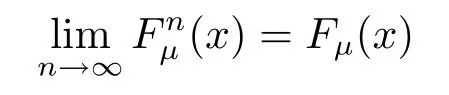
at any continuity point of Fμ(x).
Theorem 3.1If{ξn}converges in quasi-probability to ξ,then{ξn}fundamentally converges in quasi-probability.
Proof Suppose that{ξn}converges in quasi-probability to ξ,then for any given ε>0, we have
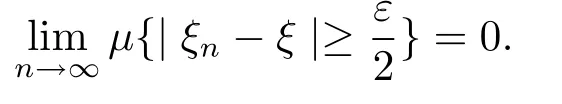
According to[2],

It follows from Theorem 2.3 that


that is ξn→ξ a.e..And since
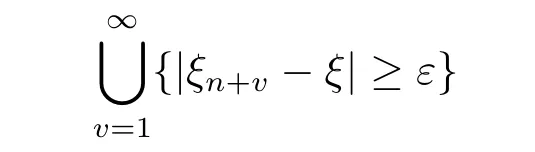
is decreasing for n,it follows from the continuity ofμthat
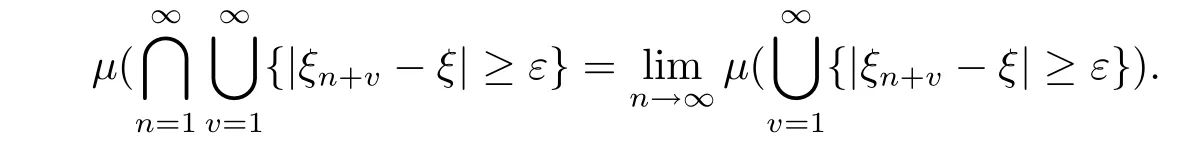
Now the theorem is proved.
Theorem 3.3[4]Suppose that ξ,ξ1,ξ2,···,ξn,···are q-random variables def i ned on the quasi-probability space(X,F,μ).If{ξn}converges almost surely to ξ,then{ξn} converges in quasi-probability to ξ.
Example 3.1[4]Suppose that ξ1,ξ2,···,ξn,···are independent q-random variables def i ned on the quasi-probability space(X,F,μ).If
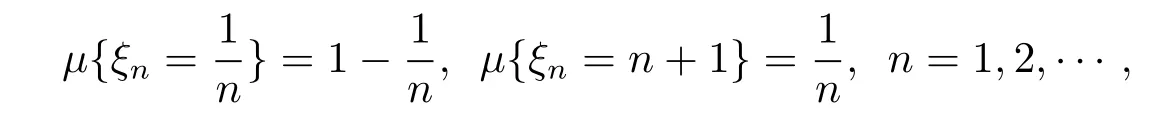
then{ξn}converges in quasi-probability to 0.However,{ξn}does not converges almost surely to 0.
Theorem3.3 shows that convergence almost surely implies convergence in quasi-probability. Example 3.1 shows that convergence in quasi-probability does not imply convergence almost surely.But for independent q-random series,convergence almost surely is equivalent to convergence in quasi-probability.
converges almost surely if and only ifconverges in quasi-probability.
Proof Assume that Fμn(x),Fμ(x)are the distribution functions of ξn,ξ,respectively. Let x,y,z be the given continuity points of the distribution function Fμ(x).
On the one hand,for any y<x,we have
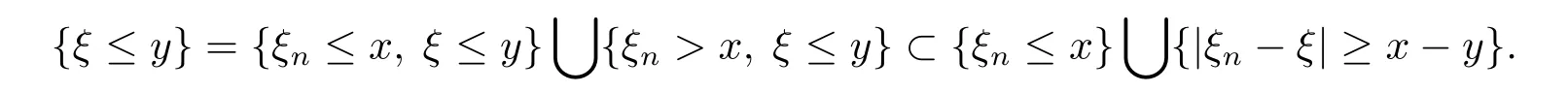
It follows from Theorem 2.3 that
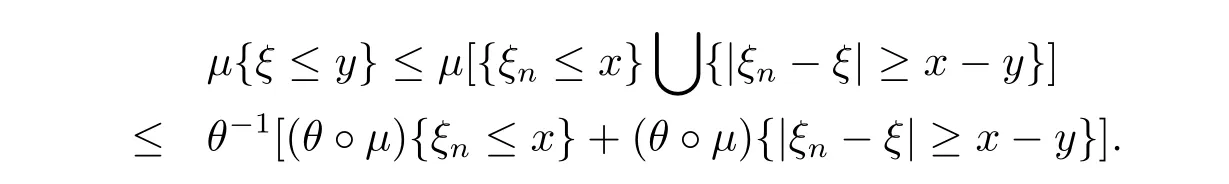
Since{ξn}converges in quasi-probability to ξ,and θ,θ-1are continuous,we have
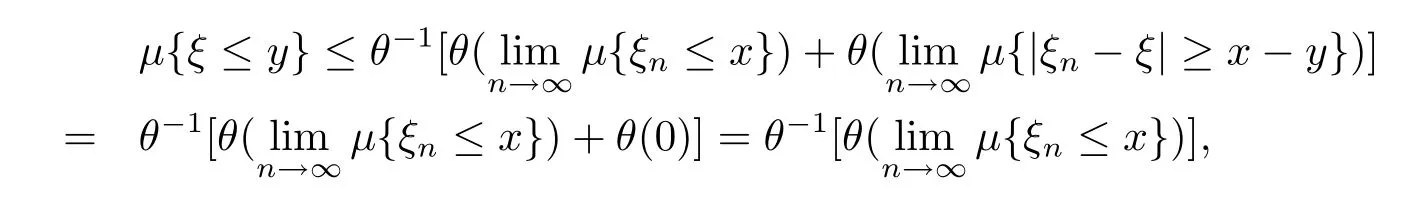
which implies that
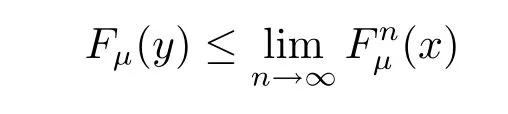
for any y<x.
Let y→x,we obtain
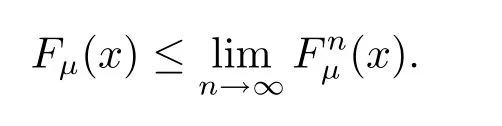
On the other hand,for any z>x,we have
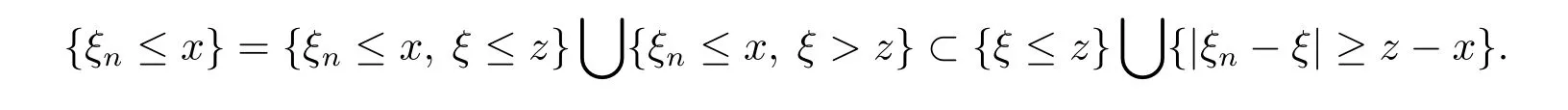
Sinceμ{|ξn-ξ|≥z-x}→0 as n→∞,and θ,θ-1are continuous,we get
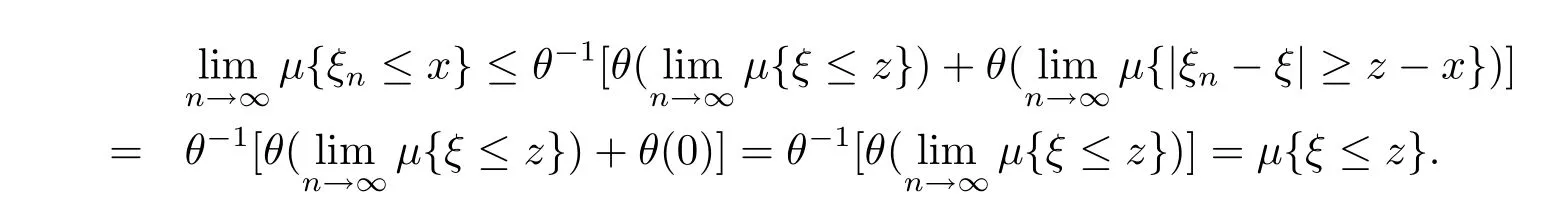
It means that
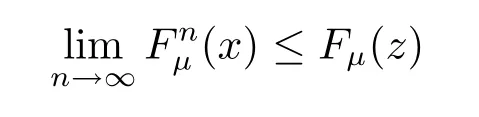
for any z>x.Let z→x,we get
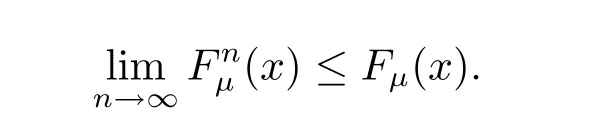
Finally,one can see that
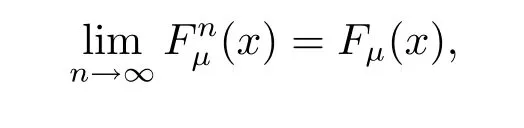
that is to say{ξn}converges in distribution to ξ.
According to Theorems 3.3 and 3.5,we conclude that convergence almost surely implies convergence in quasi-probability;convergence in quasi-probability implies convergence in distribution.
4 Conclusions
This paper proposed some new convergence concepts for quasi-random variables.Firstly, the properties of quasi-probability measure were further discussed.Secondly,the concepts of convergence in quasi-probability,convergence almost surely,convergence in distribution and convergence almost everywhere were introduced on quasi-probability space.Finally, the relationships among the convergence concepts were investigated in detail.All investigations helped to lay important theoretical foundations for the systematic and comprehensive development of quasi-probability measure theory.
[1]Chung Kailai.A course in probability theory(3rd ed.)[M].Beijing:China Machine Press,2010.
[2]Yan Shijian,Liu Xiufang.Measure and probability(2nd ed.)[M].Beijing:Beijing Normal Universiy Press,2011.
[3]Wang Weigang.The strong law of large numbers for Markov chains in general environments[J].J. Math.,2011,31(3):481-487.
[4]Zhang Chunqin,Li Chunguo.Convergence concepts on quasi-probability space[J].Ann.Fuzzy Math.Inform.,2015,10(4):537-544.
[5]Zhang Zhingming.Some discussions on uncertain measure[J].Fuzzy Optim.Dec.Mak.,2011,10(5):31-43.
[6]Wang Zhenyuan,Klir G J.Fuzzy measure theory[M].New York:Plenum Press,1992.
[7]Ha Minghu,Guo Rui,Zhang Hong.Expected value models on quasi-probability space[J].Far East J.Appl.Math.,2007,29(2):233-240.
[8]Zhang Chunqin,Yang Fang.Strong law of large numbers on quasi-probability space[J].J.Math., 2012,32(6):999-1004.
[9]Ferrie C.Quasi-probability representations of quantum theory with applications to quantum information science[J].Rep.Prog.Phys.,2011,74(2):1-24.
[10]Ha Minghu,Feng Zhifang,et al.The key theorem and the bounds on the rate of uniform convergence of statistical learning theory on quasi-probability space[J].Chin.J.Comp.,2008,31(3):476-485.
[11]Zhang Chunqin.Fuzzy renewal processes on quasi-probability space[J].Ann.Fuzzy Math.Inform., 2016,11(5):755-768.
[12]Liu Baoding.Uncertainty theory(4th ed.)[M].Beijing:Uncertianty Theory Laboratory,2012.
[13]Liu Baoding.Uncertainty theory(2nd ed.)[M].Berlin:Springer-Verlag,2007.
[14]Wang Zhenyuan,Klir G J.Generalized measure theory[M].New York:Spingger-Verlag,2008.
[15]Gianluca,Cassese.Convergence in measure under f i nite additivity[J].Indian J.Stat.,2013,75-A:171-193.
關(guān)于擬概率測(cè)度的收斂理論
張春琴,張輝
(河北大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,河北保定071002)
本文研究了擬概率空間上收斂概念之間的關(guān)系這一問(wèn)題.利用類比的方法,在擬概率空間上提出了一些新的關(guān)于擬-隨機(jī)變量的收斂概念并討論了這些收斂概念之間的關(guān)系,獲得了模糊測(cè)度下的收斂理論,推廣了關(guān)于經(jīng)典測(cè)度的收斂概念.
擬概率測(cè)度;收斂理論;收斂概念;擬-隨機(jī)變量
O159;O174.12
A
0255-7797(2017)05-0999-08
?Received date:2016-09-29Accepted date:2017-01-20
Supported by National Nature Science Foundation of China(61375075);Natural Science Foundation of Hebei Province,China(A2014201166);Natural Science Foundation of Hubei University(799207217073).
Biography:Zhang Chunqin(1979-),female,Yao,born at Guigang,Guangxi,instructor,major in statistical learning theory.
2010 MR Subject Classif i cation:28E10
- 數(shù)學(xué)雜志的其它文章
- BIFURCATION IN A RATIO-DEPENDENT PREDATOR-PREY SYSTEM WITH STAGE-STRUCTURED IN THE PREY POPULATION
- FORCING AN ω1-REAL WITHOUT ADDING A REAL
- 組織特異性蛋白質(zhì)復(fù)合體的識(shí)別
- 面板數(shù)據(jù)分位數(shù)回歸模型的參數(shù)估計(jì)與變量選擇
- ON A NEW NONTRIVIAL ELEMENT INVOLVING THE THIRD PERIODICITY γ-FAMILY IN π?S
- 兩類二元函數(shù)芽的一個(gè)共同性質(zhì)及其應(yīng)用

