基于移動窗的多核最小二乘支持向量機建模算法

李 琦， 杜 曉 東， 張 洪 略， 邢 麗 萍

( 大連理工大學 控制科學與工程學院, 遼寧 大連 116024 )

基于移動窗的多核最小二乘支持向量機建模算法

李 琦*， 杜 曉 東， 張 洪 略， 邢 麗 萍

( 大連理工大學 控制科學與工程學院, 遼寧 大連 116024 )

針對時變工業過程建模中存在的模型泛化性和適應性較低的問題，利用移動窗技術，通過使用多個核函數，提出了一種基于移動窗的多核最小二乘支持向量機(LSSVM)建模算法．該算法在最小二乘支持向量機算法基礎上，利用多核組合代替單核，增強了模型的泛化能力；利用移動窗技術，增加了模型對時變工業過程的動態辨識能力及模型的更新效率．仿真實驗結果表明，該算法具有更好的泛化性能．

動態建模；核函數；最小二乘支持向量機(LSSVM)；移動窗

0 引 言

核方法是解決非線性問題的一種很好的方法，它可以將一個線性不可分問題轉化為求解一個線性可分問題．當原始數據為非線性數據時，核函數可以把原始數據樣本映射到一個高維空間，將其處理為可分的線性數據，從而實現求解．通過這種方法，可以在不知道具體映射方法和原始數據的具體分布情況下，快速地解決高維空間映射問題，避免了常規算法對特征空間設計的煩瑣．因此越來越多的學者將核方法用于機器學習中[1-2]．目前常用的核函數有sigmoid函數、徑向基函數和線性函數等，其中應用最多的是徑向基函數．最小二乘支持向量機(least squares support vector machines，LSSVM)中大多采用徑向基函數的單核結構，但當數據分布不平坦、數據樣本異構或數據不規則、樣本規模較大時，單核構成的函數就無法滿足需求．

Lanckriet等[3]提出了多核運行的方法，即多核學習(multiple kernel learning，MKL)，通過將多個核函數線性組合代替單核．實驗結果表明，用此方法構建的模型比用單核構建的模型性能表現更出色．在處理不同的問題時，不同的核函數可以與多種建模算法相結合，從而解決不同的關鍵性問題，且兩部分互不干擾，可相輔相成形成多種不同的基于核技術的方法．在解決凸優化問題時，用交叉驗證選擇正則化參數，計算量極其煩瑣，Jian等[4]從優化內核和正則化參數的角度出發，提出了基于半定規劃(semi-definite programming，SDP)的多核學習算法，成功地避免了此缺陷，較快地形成了一個自動選擇模型的過程．Damoulas 等[5]將多核學習用于貝葉斯分類中，并用人工數據做了驗證，證明用多核代替單核可以增加決策函數的可解釋性，比單核模型的性能更好．另外，單核學習的魯棒性和泛化性較差，而在多核學習中確定核函數的問題，最終可轉化為基本核函數和相應系數的確定問題，因此比單核學習算法的可解釋性強、泛化性高[6-7]．

按照核函數權值和機器學習參數的確定順序，可將多核學習算法的求解方法分為兩類：one-step方法，two-step方法．在one-step方法中，進行一次循環便可確定核函數的權值和機器學習的參數值，再利用半定規劃SDP、二次約束型二次規劃(quadratically constrained quadratic programming)和二階錐規劃(second-order cone programming) 等求解．two-step方法是先利用機器學習的算法更新核函數權值，再利用核函數的運算更新機器學習中的相關參數，不斷重復此步驟直到最終結果達到精度要求．較常用的two-step方法是半無限線性規劃(semi-infinite linear programming)方法[8]．

本文針對時變工業過程建模問題，融合移動窗技術、LSSVM和基于lp-范數約束的多核學習等不同算法，提出一種基于移動窗的動態多核學習算法．

1 多核學習的原理

LSSVM學習結果的表達式如下：

(1)

式中：ai是拉格朗日因子；b是偏置值；xi(i=1，2，…，n)是訓練樣本，n是樣本個數；K(xi，xj)=φT(xi)φ(xj)．

(2)

其中參數向量

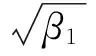
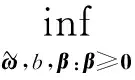
(3)

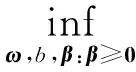
(4)

2 基于lp-范數約束的多核學習算法的研究

2.1 基于lp-范數約束的多核學習算法描述

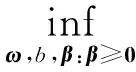
(5)

(6)

2.2 基于lp-范數約束的多核學習算法推導

算法采用Ivanov正則優化，假設表達式(5)中(ωm，b)是兩個固定值，對β求偏導，令其結果為0，得出如下等式：

(7)

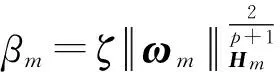
(8)

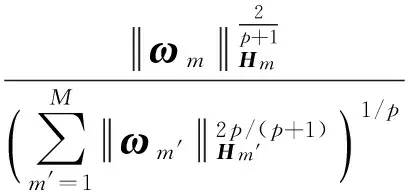
(9)

2.3 基于lp-范數約束的多核學習LSSVM算法分析

結合上述對多核學習方法的分析和LSSVM的優化過程描述，可以得到基于lp-范數約束的MKL_LSSVM的求解式：

(10)

進一步，可以得出在對偶空間中LSSVM優化問題的拉格朗日表達式：

(11)

從而可推出，對偶空間中基于lp-范數約束的MKL_LSSVM的問題等價于式(12)表達的優化問題：

(12)

(13)

由上面的推導過程可以看出，求解MKL_LSSVM最終轉換為求解線性規劃QCLP(quadratically constrained linear programming)的問題，實質為求解一個含有二次約束的線性問題．

3 基于移動窗的動態多核LSSVM算法

算法中采用式(14)求取拉格朗日因子a的值：

(14)

求取核函數β，根據LSSVM中的式(15)可以推出式(16)：

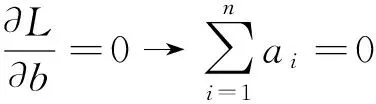
(15)

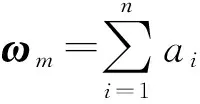
(16)

將式(16)代入式(9)，得到式(17)：

(17)

從而可以按照式(17)更新核函數權值，其多核學習的流程圖如圖1所示．

在原空間，求解基于lp-范數的多核學習算法步驟如下：

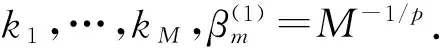
(3)執行下面步驟至滿足停止條件．

①按照式(14)求解a(t)；

②結合式(17)和(9)更新核函數的權值：

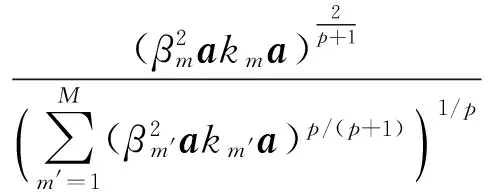
③上述算法中，如果權值的變化比較小則停止循環，即max(βm(t)-βm(t-1))≤e，其中e是一個非常小的正數．

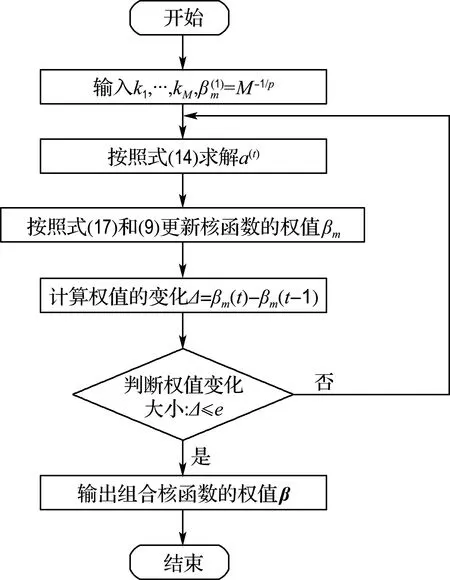
圖1 基于lp-范數的多核學習算法流程圖

考慮模型對時變工業過程的動態辨識能力，利用移動窗技術，定義移動窗長為w，對模型進行實時更新操作，以提高模型的自適應性．

同時，考慮到核函數的選取和參數的確定會間接影響輸入空間向特征空間的映射，也影響組合核函數的性能，因此樣本數據經過核函數處理變為核函數矩陣時，要對核函數矩陣進行核標準化處理．出于以上考慮選用的核函數是高斯核函數(Gaussian kernel)：

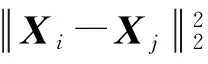
δ∈R+

(18)

在對高斯核函數進行處理時選用了球形標準化，標準化的數學表達式如下：

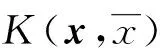
(19)

通過此操作，可以將所有輸入樣本都置換到一個半徑為1的單位球內，并且去掉了輸入樣本的量綱．

4 仿真實驗分析

實驗選取了單變量函數和多變量函數兩種函數分別對實驗對象進行仿真，其中，選用的核函數為徑向基函數，將核函數的寬度[11]設為2-2，2-1.5，…，21.5，22，之間相隔0.5；C取值為2-1，…，210；p取值[8]為1，4/3，2，4，∞．通過改變p的值來觀察模型性能的變化，定義移動窗長w=50．

(1)性能指標的選取

為了進一步清晰地說明本文提出方案的有效性，需要采用均方根誤差Erms和最大絕對值誤差Em(maximum absolute error)來評估模型的性能：

(20)

Em=max(yi-fi(x))；i=1，2，…，n

(21)

其中yi表示實際的數據樣本值，fi(x)表示按照該算法所建模型預測出來的預測值，n表示樣本個數．

(2)仿真函數模型

①單變量函數模型

模型是一個典型的非平坦的混合高斯分布函數[12]：

(22)

函數yi=r(xi)+ni，其中xi∈[0，10]，ni～N(0，0.052)．從0～10內選取均勻分布的200個樣本，偶數點的100個輸入數據作為訓練集，奇數點的100個輸入數據作為測試集．

②多變量函數模型

此模型是選取文獻[13]中提出的模型，見式(23)．其中，假定系統的輸入函數為u(t)=sin(2πt/25)+sin(2πt/10)，均勻分布在[-2，2]．e(t)是高斯白噪聲序列，定義為e(t)∈N(0，0.1)．用數學表達式對該非線性模型的表述為y(t)=f(x(t))+e(t)，其中x(t)=[y(t-1)，y(t-2)，u(t-1)]．取其中的200組數據，前100組作為訓練集，后100組作為測試集．

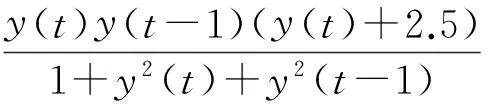
(23)

(3)實驗結果分析

對兩個函數分別單獨實驗10次，取每次實驗的平均值為相應實驗的最終結果．對于式(22)，LSSVM的參數C=210，δ=0.4時最優；對于式(23)，LSSVM的參數C=210，δ=0.1時最優．

表1和表2分別表示單變量函數采用靜態多核學習和帶移動窗的動態多核學習情況下的測試結果，表3和表4分別表示多變量函數采用靜態多核學習和帶移動窗的動態多核學習情況下的測試結果．

從表1和表2可以看出，對于不同的p值，模型的測試結果不同，p值越大，模型的Erms和Em越小，說明測試值越接近于真實值，模型的預測效果越好．將表1與表2對比可以發現，前者的Erms和Em都遠遠大于后者，但模型所耗時間均遠小于后者．說明函數在帶移動窗的動態多核學習下，學習效果要優于靜態多核學習效果，動態多核學習下的模型，預測精度更高．由于動態模型具有自適應性，若當前模型不合適時，需要更新模型，故其計算量較大，所耗時間較長．

表1 單變量函數在不同lp-范數下的靜態多核學習測試結果

Tab.1 The test results of one-variable function based on differentlp-norm static MKL

pErmsEmt/s14/324∞0.00810.00640.00500.00410.00360.07240.05270.03810.02440.01890.98520.74431.01650.99951.1789

表2 單變量函數在不同lp-范數下的帶移動窗的動態多核學習測試結果(w=50)

Tab.2 The test results of one-variable function based on differentlp-norm dynamic MW_MKL (w=50)

pErms/10-4Emt/s14/324∞2.37041.80861.33151.03770.78360.00160.00110.00080.00050.00035.83394.63275.26864.07229.6058

從表3和表4可以看出，不同于單核函數，模型的預測效果并不會隨著p值的增大而變好，p值過小或過大，模型的性能都會降低．p=4/3時，模型的預測效果最好．同樣對比表3和表4，可以發現：函數在帶移動窗的動態多核學習下，模型的誤差較小，擬合效果較好，學習效果要優于靜態多核學習效果．但是對于多變量函數，帶移動窗的動態多核學習算法基本上比靜態多核學習算法所耗時間長，但兩者計算復雜度差別不是特別大．

表3 多變量函數在不同lp-范數下的靜態多核學習測試結果

Tab.3 The test results of multivariable function based on differentlp-norm static MKL

pErmsEmt/s14/324∞0.01970.01940.02030.02120.02230.06310.06130.06980.06510.07164.28813.06792.93792.92433.1722

表4 多變量函數在不同lp-范數下的帶移動窗的動態多核學習測試結果(w=50)

Tab.4 The test results of multivariable function based on differentlp-norm dynamic MW_MKL (w=50)

pErms/10-4Emt/s14/324∞3.76433.62973.85563.98674.10570.002160.002030.002150.002200.002234.01333.69333.93233.63604.0298

5 結 語

針對復雜時變工業過程建模問題，提出了基于移動窗的動態多核LSSVM算法，將移動窗技術與傳統的靜態多核學習方法相結合，利用多核組合代替傳統的單核，并給出了相關算法的步驟描述．最后用單變量函數和多變量函數兩個非線性函數進行了實驗仿真，結果驗證了所提方法構建的模型性能優于傳統的靜態多核學習方法，模型的泛化性更好．

[1] WORTON B J. Kernel methods for estimating the utilization distribution in home-range studies [J].Ecology, 1989,70(1):164-168.

[2] 張凱軍,梁 循. 一種改進的顯性多核支持向量機[J]. 自動化學報, 2014,40(10):2288-2294.

ZHANG Kaijun, LIANG Xun. An improved domain multiple kernel support vector machine [J].ActaAutomaticaSinica, 2014,40(10):2288-2294. (in Chinese)

[3] LANCKRIET G R G, CRISTIANINI N, BARTLETT P,etal. Learning the kernel matrix with semidefinite programming [J].JournalofMachineLearningResearch, 2004,5:27-72.

[4] JIAN Ling, XIA Zhonghang, LIANG Xijun,etal. Design of a multiple kernel learning algorithm for LS-SVM by convex programming [J].NeuralNetworks, 2011,24(5):476-483.

[5] DAMOULAS T, GIROLAMI M A. Pattern recognition with a Bayesian kernel combination machine [J].PatternRecognitionLetters, 2009,30(1):46-54.

[6] 汪洪橋,孫富春,蔡艷寧,等. 多核學習方法[J]. 自動化學報, 2010,36(8):1037-1050.

WANG Hongqiao, SUN Fuchun, CAI Yanning,etal. On multiple kernel learning methods [J].ActaAutomaticaSinica, 2010,36(8):1037-1050. (in Chinese)

[7] 楊 柳,張 磊,張少勛,等. 單核和多核相關向量機的比較研究[J]. 計算機工程, 2010,36(12):195-197.

YANG Liu, ZHANG Lei, ZHANG Shaoxun,etal. Comparison research of single kernel and multi-kernel relevance vector machine [J].ComputerEngineering, 2010,36(12):195-197. (in Chinese)

[8] KLOFT M, BREFELD U, SONNENBURG S,etal.lp-norm multiple kernel learning [J].JournalofMachineLearningResearch, 2011,12:953-997.

[9] IVANOV V K, VASIN V V, TANANA V P.TheoryofLinearIll-PosedProblemsanditsApplications[M]. Berlin: Walter de Gruyter, 2002.

[10] TIKHONOV A N, ARSENIN V Y.SolutionsofIll-PosedProblems[M]. New York: VH Winston & Sons, 1977.

[11] ZHANG Xiangrong, HU Longying, ZHANG Lin. An efficient multiple kernel computation method for regression analysis of economic data [J].Neurocomputing, 2013,118:58-64.

[12] CEPERIC V, GIELEN G, BARIC A. Sparse multi-kernel support vector regression machines trained by active learning [J].ExpertSystemswithApplications, 2012,39(12):11029-11035.

[13] CAI Yanning, WANG Hongqiao, YE Xuemei,etal. A multiple-kernel LSSVR method for separable nonlinear system identification [J].JournalofControlTheoryandApplications, 2013,11(4):651-655.

MultiplekernelLSSVMmodelingalgorithmbasedonmovingwindow

LI Qi*, DU Xiaodong, ZHANG Honglüe, XING Liping

( School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China )

In order to solve the problem of modeling in the time-varying industrial process which has lower modeling generalization and adaptation, a multiple kernel least squares support vector machines (LSSVM) modeling algorithm based on moving window technology is proposed by using multiple kernel functions. Multiple kernel groups are used to replace single kernel in this algorithm based on least squares support vector machines, which can improve model′s generalization performance. The algorithm increases the dynamic recognition ability for the time-varying industrial process and updated efficiency of model through moving window technology. The simulation result shows that the algorithm has better generalization performance.

dynamic modeling; kernel function; least squares support vector machines(LSSVM);moving window

2017-01-04；

2017-07-17．

國家自然科學基金資助項目(61403058)；中央高校基本科研業務費專項資金資助項目(DUT14LAB15).

李 琦*(1979-)，男，博士，副教授，E-mail:qili@dlut.edu.cn.

1000-8608(2017)05-0511-06

TP273

A

10.7511/dllgxb201705011