基于改進PSO算法的SVM在甲烷測量中的應用*

鮑 立,陳紅巖,郭晶晶,袁月峰,李孝祿

(中國計量大學機電工程學院,杭州 310018)

基于改進PSO算法的SVM在甲烷測量中的應用*

鮑 立,陳紅巖*,郭晶晶,袁月峰,李孝祿

(中國計量大學機電工程學院,杭州 310018)

針對甲烷氣體定量分析過程中,傳統SVM模型預測精度低、收斂速度慢等問題,提出了一種基于改進PSO算法的SVM回歸模型。該模型在傳統PSO算法尋優的基礎上,引入動量項的同時增加隨機粒子個體極值的追隨因子,使粒子不僅追隨全局最優解和局部最優解,還跟隨種群中任一粒子的個體極值,使得尋優算法后期收斂速度較快,不易陷入局部最小值。實驗中,對0～5.05%濃度的25組標準甲烷樣氣進行建模分析,并與傳統PSO算法尋優模型和Grid搜索法尋優模型進行對比。結果表明,采用改進PSO算法建立的SVM回歸模型均方根誤差小,收斂速度快。

檢測技術與自動化裝置;SVM;改進PSO算法;回歸分析;紅外甲烷傳感器

隨著國民經濟的不斷發展,對采礦行業的需求與日俱增,但要保證煤礦開采安全順利的進行,對甲烷的測量精度具有較高的要求,因為甲烷氣體屬于易燃易爆危險氣體,稍有不慎就會引發爆炸,造成重大的人員傷亡和經濟損失。目前,由于紅外甲烷傳感器[1]測量精度較高,使用壽命較長,越來越多的被用于煤礦開采過程中甲烷氣體的測量。但其測量精度仍需進一步提高,以確保工作人員的生命財產安全。

近些年來,眾多國內外學者致力于如何減小甲烷氣體的測量誤差,提出了許多方法,如分段插值法、最小二乘法、多元回歸、小波神經網絡以及SVM等。John Leis等[2]針對固態紅外光源的光學通量易受溫度影響的問題,提出了利用脈沖結電壓測量發射的紅外通量并引入補償算法;梁永直等[3]在最小二乘法的基礎上提出了改進的分段最小二乘法,減小了擬合誤差,節省了存儲空間,加快了運算速度;李卯東等[4]提出了改進的BP神經網絡算法,克服了傳統最小二乘法擬合時計算復雜、誤差較大的缺點;曲健等[5]提出了利用改進的網格搜索法進行SVM核函數參數尋優,建立出預測精度較高、用時較短的SVM回歸模型;劉文貞等[6]在傳統單核SVM的基礎上提出了一種混合核ε-SVM,對汽車尾氣進行定量分析,提高了模型的泛化能力以及預測精度。

由于SVM具有小樣本學習能力強、預測誤差小以及泛化能力好等突出優點,已被廣泛應用于許多領域。本文在前人的基礎上提出了一種基于改進PSO算法的SVM,采用紅外甲烷傳感器對濃度范圍在0～5.05%的25組甲烷標準樣氣進行采集,將其中20組數據作為訓練集建立SVM回歸模型,5組數據作為測試集驗證模型的預測精度。

1 SVM回歸模型

SVM[7-8]是由Vapnik等人根據統計學習理論中結構風險最小化原則提出的,它能夠盡量提高學習機的推廣能力,即使由有限數據集得到的判別函數對獨立的測試集仍能夠取得較小的誤差,此外,SVM是一個凸二次優化問題,能夠保證找到的極值解就是全局最優解。SVM回歸分析模型利用核函數將紅外甲烷傳感器測量得到的原始數據映射到高維空間,然后在高維空間進行回歸分析,建立紅外甲烷傳感器測量輸出的電壓差值比與待測甲烷氣體濃度的回歸模型。

本文將甲烷濃度值和對應的紅外甲烷傳感器測量輸出的電壓差值比構成數據集T={(x1,y1),…,(xl,yl)}∈(R×R),其中,xi∈R為紅外甲烷傳感器輸出的電壓差值比,yi∈R為對應的甲烷濃度值,i=1,2,…,l。按照式(1)進行回歸分析:

f(xi)=ω·φ(xi)+b

(1)

式中:ω為回歸系數,φ(xi)為輸入空間到特征空間的映射函數,b為閾值。

優化問題可以轉化為如下最小化式:

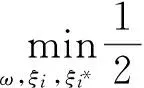
(2)

(3)

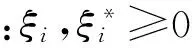
引入Lagrange函數求解式(2)和式(3),通過核函數K(xi,xj)將高維空間的內積運算轉換到原二維空間計算,有:

(4)

(5)

經求解得到:

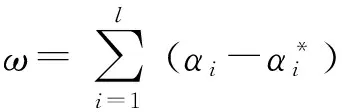
(6)

從而可以得到SVM模型的回歸函數為:

(7)

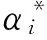
在SVM建模過程中常用到的核函數有線性核函數、多項式核函數、徑向基(RBF)核函數以及兩層感知器核函數。本文選擇RBF核函數,其表達式如下:

K(xi,xj)=exp(-g‖xi-xj‖2)g>0

(8)

式中:參數g為核函數中gamma參數,若k為屬性的數目,則g默認為1/k。

2 改進的PSO算法

在使用SVM建立回歸模型分析時,想要得到較滿意的結果,需要調整相關參數(主要是懲罰因子C和核函數參數g)才能得到比較理想的預測準確率。本文選擇PSO算法實現SVM的參數尋優[9-10],但是傳統的PSO 算法存在后期收斂速度緩慢、易陷入局部極小點等問題,為了同時克服這些缺陷,本文在引入動量項的同時增加隨機粒子個體極值的追隨因子,使得粒子不僅追隨全局最優解和局部最優解,還跟隨種群中任一粒子的個體極值以達到既緩和后期震蕩又解決后期趨同的目的。

傳統的PSO算法速度和位置更新公式為:

(9)

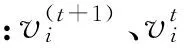
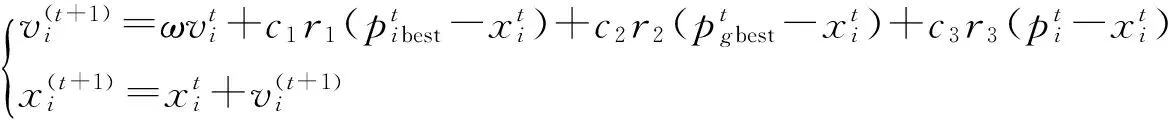
(10)

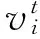
(11)

改進后的粒子群速度和位置更新公式為:

(12)

動量項的引入使得算法在修正粒子速度時,不僅考慮了個體最優值和全局最優值,還考慮了速度修正量歷史變化趨勢的影響,從而減小了進化過程中的震蕩。此外,在粒子的迭代過程中,通過pgbest、pibest和pi共同向下一代傳遞信息,增大了粒子所獲得的信息量。由于pi的權重值很小,相當于在原有基礎上增加了一個小能量干擾以實現粒子的多樣性,從而避免了算法的過分早熟。

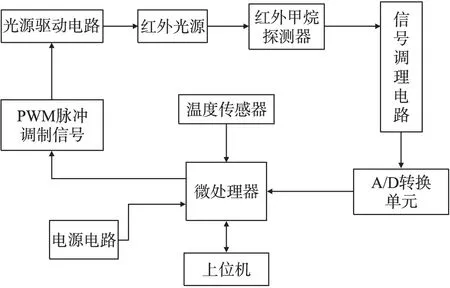
圖1 紅外甲烷傳感器檢測原理框圖

3 實驗分析

本實驗采用紅外吸收光譜原理[1]制作的甲烷傳感器對濃度范圍在0～5.05%的25組標準甲烷樣氣進行測量,其輸出為測量通道和參考通道的電壓差與參考通道電壓的比值。該紅外甲烷傳感器檢測原理框圖如圖1所示,上位機界面如圖2所示,測量數據見表1。選擇其中20組數據作為訓練集,建立SVM回歸模型并檢驗模型在訓練集上的回歸效果;選擇濃度為0.35、1.38、2.42、3.52、4.79的5組數據作為測試集,用建立好的回歸模型進行預測,驗證SVM回歸模型的預測精度和水平[11]。

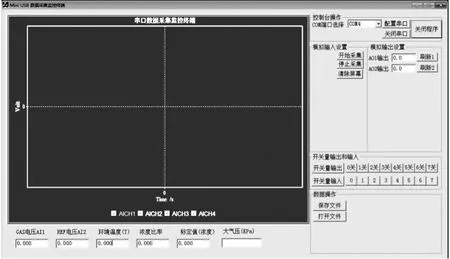
圖2 上位機界面

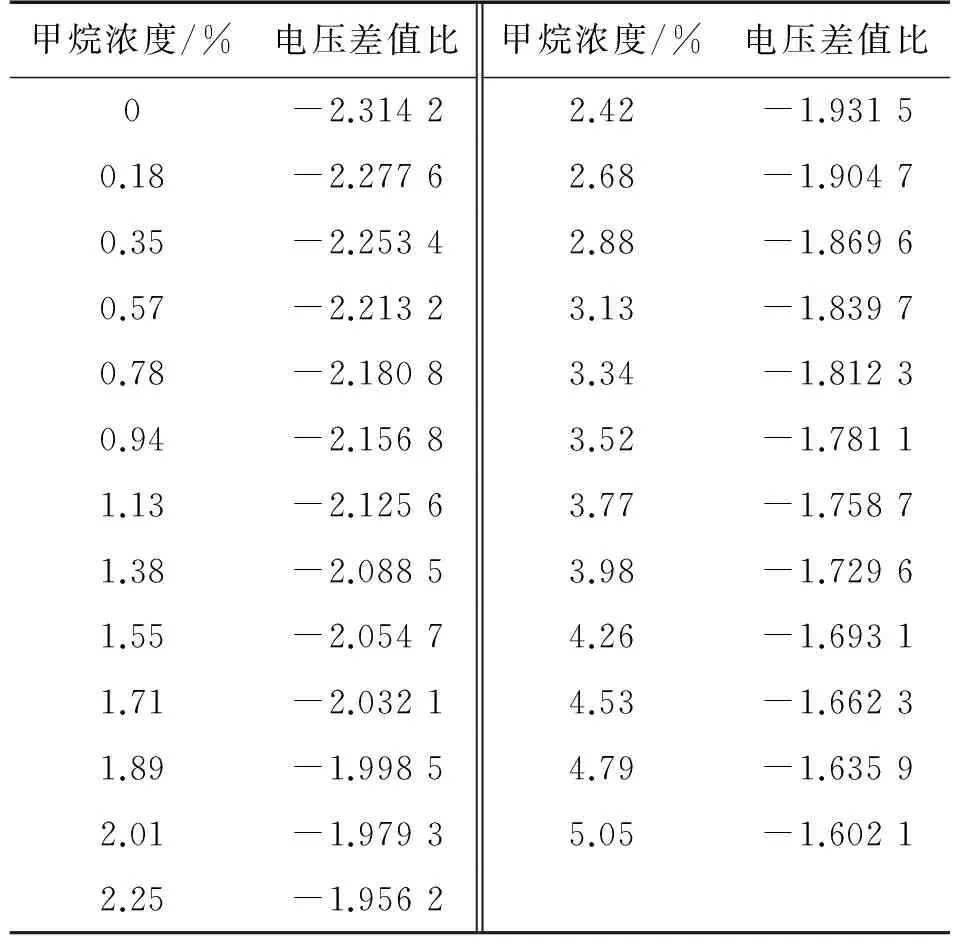
甲烷濃度/%電壓差值比甲烷濃度/%電壓差值比0-2.31422.42-1.93150.18-2.27762.68-1.90470.35-2.25342.88-1.86960.57-2.21323.13-1.83970.78-2.18083.34-1.81230.94-2.15683.52-1.78111.13-2.12563.77-1.75871.38-2.08853.98-1.72961.55-2.05474.26-1.69311.71-2.03214.53-1.66231.89-1.99854.79-1.63592.01-1.97935.05-1.60212.25-1.9562

模型的建立需要找到最優的懲罰因子C和RBF核函數參數g,本文采用改進的PSO算法進行參數尋優,選擇最小化式(13)所示的均方根誤差函數為目標函數,選擇適應度函數為式(14)所示,

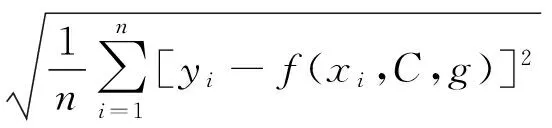
(13)

Ffitness=Fmse(C,g)

(14)

參數尋優具體步驟如下:

輸入:粒子的維數和個數;

輸出:SVM最佳參數組合(C,g)。

①初始化。隨機初始化SVM參數組合(C,g)在解空間中的位置、粒子的初始位置和速度,設置粒子的最大速度vmax、最大迭代次數、權重取值范圍以及SVM各參數取值范圍。

②計算每個粒子的適應度值。設置每個粒子的個體極值pibest為當前位置,根據式(14)計算每個粒子的適應度值,取適應度值最優的粒子個體極值為最初的全局極值pgbest。

③根據式(12)更新粒子的速度和位置,根據式(13)、式(14)更新適應度值Ffitness,令pipresent=Ffitness。

④比較當前粒子的個體最優極值pibest和當前適應度值pipresent,若pipresent>pibest,則pipresent=Fibest。

⑤比較更新之后pipresent和全局最優位置pgbest的大小,其中較小的即為最終的全局最優解。

⑥判斷是否滿足迭代終止條件,滿足則停止迭代,輸出最優的SVM參數組合,不滿足則轉步驟②。當使得最優解的參數組合不唯一時,取C值最小的那組。

目前,學者們普遍采用傳統PSO算法和Grid搜索法[5]來進行SVM參數尋優。為了顯示改進PSO算法優化SVM參數的優勢,本文分別采用3種尋優方法建立SVM回歸模型,進行對比分析。表2為3種尋優方法建立SVM回歸模型時的最優參數、所需時間以及均方根誤差。

表2 模型參數尋優對比

圖3～圖5分別為3種尋優方法建立SVM回歸模型時在訓練集上驗證模型回歸效果圖[12-13]。

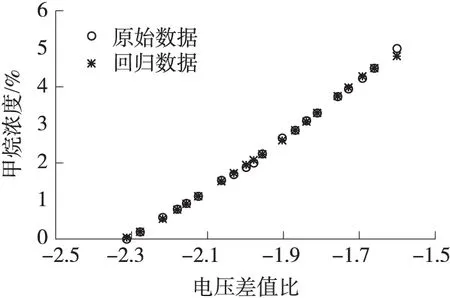
圖5 改進PSO算法-SVM

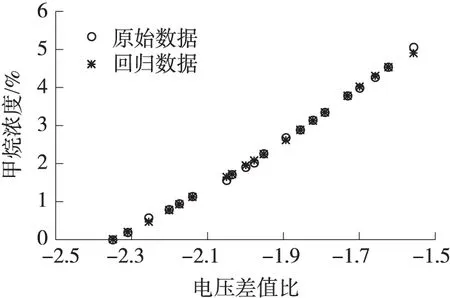
圖3 傳統PSO算法-SVM

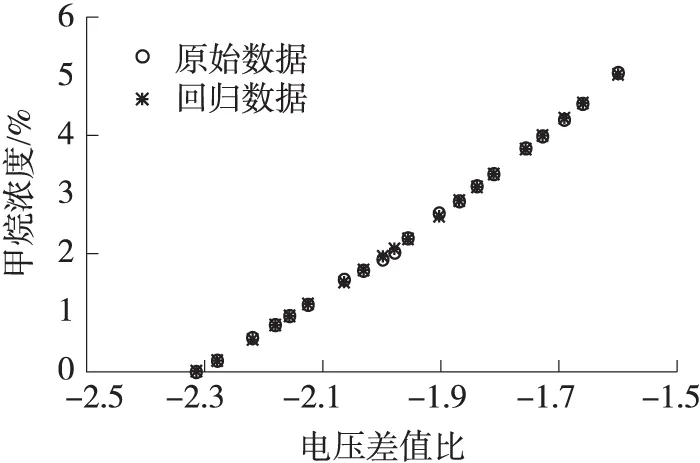
圖4 Grid搜索法-SVM

由表2可知采用改進PSO算法尋優得到的參數C明顯小于傳統PSO算法和Grid搜索法,而過大的C容易引起模型的過學習;尋優時間明顯縮短;并且均方根誤差最小。由圖3到圖5對比可知采用改進PSO算法建立SVM回歸模型的回歸效果最好。

將改進PSO算法尋優得到的最優參數組合(C,g)=(1.253 8,1.624 5)代入SVM建立模型并進行預測分析,可以得到模型的預測結果如圖6所示[14]。從圖6可以看出基于改進PSO算法的SVM模型預測曲線很好的逼近期望曲線,達到較高的預測精度。

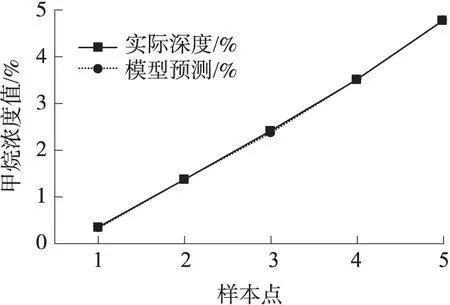
圖6 甲烷氣體模型預測輸出與期望輸出對比圖

3種模型預測誤差對比如表3所示。

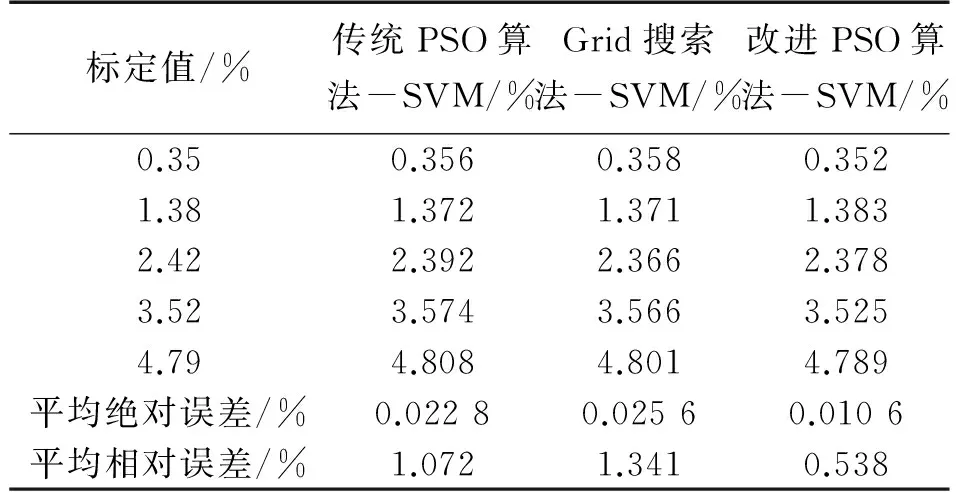
表3 模型預測誤差對比

由表3可知,基于改進PSO算法-SVM模型預測的絕對誤差和相對誤差都明顯低于傳統PSO算法-SVM模型和Grid搜索法-SVM模型,并且絕對誤差小于0.1%,相對誤差小于5%,滿足行業內對甲烷測量誤差的要求。

4 結論

本文在傳統的PSO算法尋優的基礎上,引入動量項的同時使得粒子不僅追隨全局最優解和局部最優解,還跟隨種群中任一粒子的個體極值以達到既緩和后期震蕩又解決后期趨同的目的,使得尋優算法后期收斂速度較快,不易陷入局部最小值。通過采用3種尋優方法建立SVM回歸模型進行對比分析,結果表明,改進的PSO算法尋優速度最快,建立的SVM模型回歸效果最好,預測精度最高。因此,該方法可以考慮用于煤礦開采過程中甲烷氣體的定量分析,在一定程度上可以提高甲烷的預測精度,給工作人員的生命財產安全增加保障。

[1] 譚秋林. 紅外光學氣體傳感器及檢測系統[M]. 北京:機械工業出版社,2013:1-139.

[2] John Leis,David Buttsworth. A Temperature Compensation Technique for Near-Infrared Mathane Gas Threshold Detection[J]. IEEE Transactions on Industrial Electronics,2016,63(3):1813-1821.

[3] 梁永直,李卯東,夏路易,等. 紅外甲烷傳感器檢測中的算法研究[J]. 儀表技術與傳感器,2012,27(11):149-150.

[4] 李卯東,梁永直. 基于遺傳優化的BP神經網絡法在甲烷檢測中的應用[J]. 工礦自動化,2013,39(2):51-53.

[5] 曲健,陳紅巖,劉文貞,等. 基于改進網格搜索法的支持向量機在氣體定量分析中的應用[J]. 傳感技術學報,2015,28(5):774-778.

[6] 劉文貞,陳紅巖,李孝祿,等. 基于自適應變異粒子群算法的混合核ε-SVM在混合氣體定量分析中的應用[J]. 傳感技術學報,2016,29(9):1464-1470.

[7] 王宏偉,韓云濤,彭繼慎. 基于TSPSO支持向量機紅外甲烷傳感器動態補償[J]. 傳感技術學報,2013,26(9):1193-1197.

[8] 張麗. 基于支持向量機的礦用紅外瓦斯檢測系統研究[D]. 北京:中國礦業大學(北京),2010.

[9] 鄒心遙,陳敬偉,姚若河. 采用粒子群優化的SVM算法在數據分類中的應用[J]. 華僑大學學報(自然科學版),2016,37(2):171-174.

[10] 王利霞. 改進的粒子群優化算法及其在數據分類中的應用[D]. 西安:西安電子科技大學,2014.

[11] 曲健,陳紅巖,劉文貞,等. 基于自適應變異粒子群優化的SVM在混合氣體分析中的應用[J]. 傳感技術學報,2015,28(8):1262-1268.

[12] 王小川,史峰,郁磊,等. MATLAB神經網絡43個案例分析[M]. 北京:北京航空航天大學出版社,2013:1-394.

[13] 余勝威. MATLAB優化算法案例分析與應用(進階篇)[M]. 北京:清華大學出版社,2015:298-310.

[14] 徐云升,黎瑞珍,張鐵濤,等. 實驗數據處理與科技繪圖[M]. 華南理工大學出版社,2010:1-176.

鮑立(1991-),男,漢族,安徽省安慶市,在讀研究生,主要研究方向為檢測技術與物聯網,2298926413@qq.com;

陳紅巖(1965-),男,浙江杭州市,教授,研究生導師,浙江大學內燃機工程專業碩士、博士學位;上海交通大學動力與機械工程專業博士后。主要研究領域為汽車電子、發動機排放與控制、氣體檢測等,bbchy@163.com。

ApplicationofSVMBasedonImprovedParticleSwarmOptimizationAlgorithminMethaneMeasurement*

BAOLi,CHENHongyan*,GUOJingjing,YUANYuefeng,LIXiaolu

(College of Mechanical and Electrical Engineering,China Jiliang University,Hangzhou 310018,China)

In the process of methane gas quantitative analysis,the traditional SVM model has some problems of low prediction precision and slow convergence speed and so on. To solve these problems,a SVM regression model based on improved PSO algorithm is presented. On the basis of the traditional PSO algorithm,the model introduces momentum and simultaneously increases following factors for the individual extremum of random particles to make the particles not only follow the global optimal solution and local optimal solution,follow the individual extremum of any particle in the population. This method makes optimum algorithm have a faster convergence speed and be not easy to fall into local minimum. In experiments,building a model and analyzing for 25 groups of methane gas that the concentration is range from 0 to 5.05%,and then doing a comparison with traditional PSO algorithm and Grid search method. Results show that the SVM regression model based on improved PSO algorithm has a smaller root-mean-square error and faster convergence speed.

detection technique and automatic device;SVM;improved particle swarm optimization algorithm;regression analysis;infrared methane sensor

項目來源:浙江省大學生科技創新活動計劃暨新苗人才計劃項目(省級)(2016R409)

2017-02-23修改日期:2017-04-14

TP274.2

:A

:1004-1699(2017)09-1454-05

10.3969/j.issn.1004-1699.2017.09.026