OCTEON處理器上實現國密SM2算法整體優化方案研究
李 楊 王勁林 曾學文 葉曉舟
1(中國科學院聲學研究所國家網絡新媒體工程技術研究中心 北京 100190)2(中國科學院大學 北京 100190)
OCTEON處理器上實現國密SM2算法整體優化方案研究
李 楊1,2王勁林1曾學文1葉曉舟1
1(中國科學院聲學研究所國家網絡新媒體工程技術研究中心 北京 100190)2(中國科學院大學 北京 100190)
SM2橢圓曲線公鑰密碼算法的核心運算是橢圓曲線上點乘算法,因此高效實現SM2算法的關鍵在于優化點乘算法。對橢圓曲線的點乘算法提出從底層到高層逐層優化的整體方案。上層算法使用帶預計算的modified-wNAF算法計算點乘,中間層使用a=-3的Jacobian投影坐標系計算點加和倍點,底層基于OCTEON平臺的大數乘加指令使用匯編程序實現模乘算法。最終在OCTEON CN6645處理器上實現該算法,實驗結果表明:SM2數字簽名速度提高了約540%,驗證提高了約72%,加密提高了169%,解密提高了61%。
SM2 橢圓曲線密碼算法 點乘 OCTEON處理器
0 引 言
橢圓曲線密碼體系ECC是1985年由Koblitz[1]和Miller[2]提出的,由于其使用密鑰長度短,安全性高等特點已經被廣泛應用。SM2橢圓曲線公鑰密碼算法[3],是由國家密碼管理局于2010年發布的一種基于ECC的公鑰密碼算法。SM2算法的軟件實現中,加解密和簽名驗證等操作都是基于橢圓曲線上的點乘算法實現的。因此如何高效地實現點乘運算成為提高SM2算法實現性能的關鍵。OCTEON 處理器[4]是Cavium公司推出的一款基于cnMIPS II架構的多核64位通用型處理器。本文結合OCTEON處理器的特點,對點乘算法按運算層次從低至高逐層優化,提高點乘的運算效率,從而達到對基于OCTEON處理器上實現國密SM2算法整體優化的目的。
1 基礎知識介紹
1.1 SM2算法
SM2橢圓曲線公鑰密碼算法,是由國家密碼管理局于2010年12月發布的第21號公告中公布的密碼行業標準。標準中規定了SM2數字簽名算法,SM2密鑰交換協議和SM2公鑰加密算法;并在最后給出了一組推薦曲線,如圖1所示。

圖1 SM2橢圓曲線公鑰密碼算法曲線參數
1.2 ECC數學定義和定理介紹[5]
定義1在有限域Fp(p>3)上,Weierstrass方程:
y2=x3+ax+ba,b∈Fp(4a3+27b2)modp≠0
(1)
所確定的曲線稱為有限域Fp上的橢圓曲線,滿足式(1)的所有點(x,y)及無窮遠點O共同構成了橢圓曲線上的點。即:E(Fp)={(x,y) |x,y∈Fp,且滿足方程式(1)}∪{O}。橢圓曲線E(Fp)上點的數目用#E(Fp)表示,稱為橢圓曲線的階。如果橢圓曲線上存在一個點G使得(#E(Fp))G=O,則稱點G為橢圓曲線的基點。n是#E(Fp)的素因子,稱為基點G的階,余因子h=#E(Fp)/n。
由定義1可知,橢圓曲線E(Fp)可由參數(p,a,b,n,G,h)確定。下面我們給出橢圓曲線上的群運算法則:
定義2E(Fp)上的所有點按照下面的加法運算規則,構成一個Abel群:
a)O單位元;對于?P∈E(Fp),滿足P+O=O+P=P;
b) 負元素;對于?P∈E(Fp),P的負元素-P=(x,-y),P+(-P)=O,此外-O=O;
c) 點加;P1= (x1,y1) ∈E(Fp){O},P2= (x2,y2) ∈E(Fp){O},P3= (x3,y3) =P1+P2≠O,則:
(2)
d) 倍點;P1= (x1,y1) ∈E(Fp){O},P1≠-P1,P3= (x3,y3) = 2P1,則:
(3)
定義3設P是橢圓曲線E(Fp)上點,k為正整數,則k與P的點乘(標量乘)記為:

(4)
橢圓曲線上計算點乘有多種方法,目前高效計算標量乘的算法主要有:二進制法、加減法,窗口法、帶符號的二進法、雙基數法、優化定義域法、m進制法等。當前標準的橢圓曲線標量乘法是 IEEE P1363標準中給出的投影坐標下非臨界標準型NAF(Non-Adjacent-Form)的二進制法。其基本思想是將點乘運算轉化為一系列的點加和倍點運算。
1.3 OCTEON系列處理器介紹
OCTEON系列芯片是Cavium公司推出的一款基于Cavium Networks MIPS II (簡稱cnMIPS II)架構的多核64位通用型處理器,廣泛集成了L3-L7的數據、內容。安全服務的硬件加速選項。本系統設計使用OCTEON CN66XX處理器[4],8級流水線,雙指令體系結構,核心頻率1 200 MHz。除此之外,OCTEON CN66XX還具有大數乘法指令,包括128位和256位的大數乘加指令,具體大數指令的功能和應用例子如表1所示。
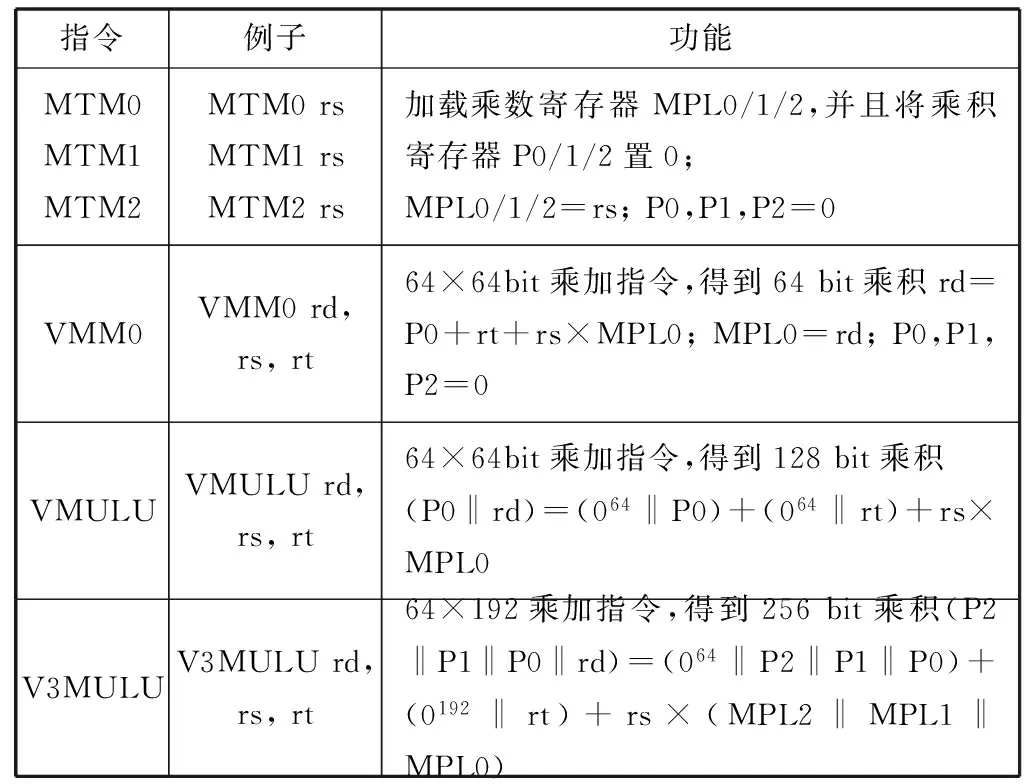
表1 OCTEON CN68XX指令列表及功能介紹
2 SM2算法整體優化方案
SM2橢圓曲線密碼算法的實現主要可以分為三個層次,如圖2所示,分別為:SM2密碼協議層,橢圓曲線群操作層和有限域操作層。有限域操作層主要是實現有限域最基本的模運算;橢圓曲線群操作層是基于模運算實現的點加和倍點運算,在此基礎上再實現點乘運算;SM2密碼協議層基于有限域和橢圓曲線群操作的基礎,實現上層的數字簽名驗證,密鑰交換和公鑰加解密等協議。層次由下而上,上層調用下層,下層是上層的基礎。
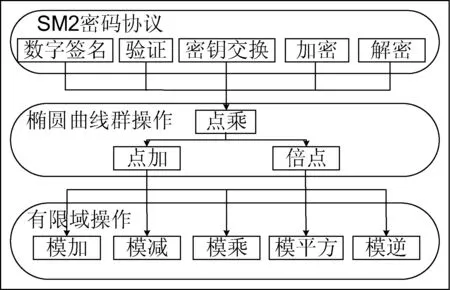
圖2 SM2橢圓曲線公鑰密碼算法實現層次結構圖
基于這一實現層次,我們可以將SM2算法整體設計和優化分為三個層次:上層點乘算法設計優化、中間層點加和倍點運算方法設計優化和下層有限域大數計算方法設計優化。
2.1 有限域大數計算方法設計優化
在有限域的底層操作中,最基本且最耗時的操作是大數模乘/模平方操作。因此本節主要使用OCTEON平臺上特有的大數乘加指令來優化模乘或平方操作。
1985年,Montgomery[6]提出的Montgomery模乘算法是現在應用最廣泛的一種模乘算法。其基本思想是用簡單省時的加法和移位操作代替普通模乘方法中費時的求逆和除法操作。其計算結構如圖3所示,其中Montgomery模乘:MM(A,B)=A×B×R-1modN;普通模乘:M(A,B)=A×BmodN。

圖3 Montgomery模乘計算結構示意圖
1996年Koc等[7]對各種Montgomery模乘算法的實現方法進行了分析總結,并歸納了5種主要的改進Montgomery算法:SOS、CIOS、FIOS、FIPS和CIHS。目前效率較高且應用最為廣泛的算法為CIOS算法。本節針對CIOS算法使用OCTEON平臺上特有的64×64 bit大數乘加指令,對SM2算法中需要用到的256 bit大數模乘運算進行優化。
使用CIOS方法計算Montgomery模乘如算法1所示。可以看出,其需要計算的關鍵步驟為:(C,S)=t[j]+A[j]B[i]+C,t[j]=S(i固定,j∈[0,s-1])。其實質就是計算一個乘數固定的帶進位的乘加運算,其中運算使用2.3節介紹的VMULU乘加指令直接實現。使用匯編算法直接實現256位CIOS算法見圖4所示,由于為64位處理器,256位操作數A,B,N可以表示為4個字。
算法1CIOS Montgomery算法
輸入:A,B,N,N′[0],其中N′[0]=-N0-1mod 2w,s為N字數
輸出:A*B*R-1modN
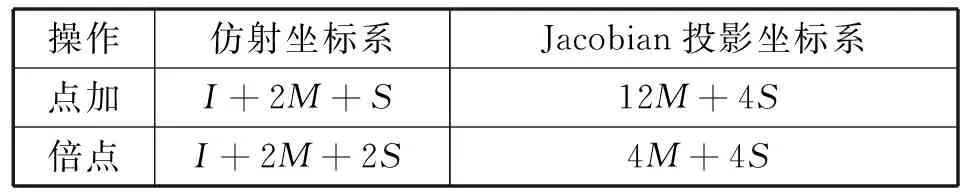
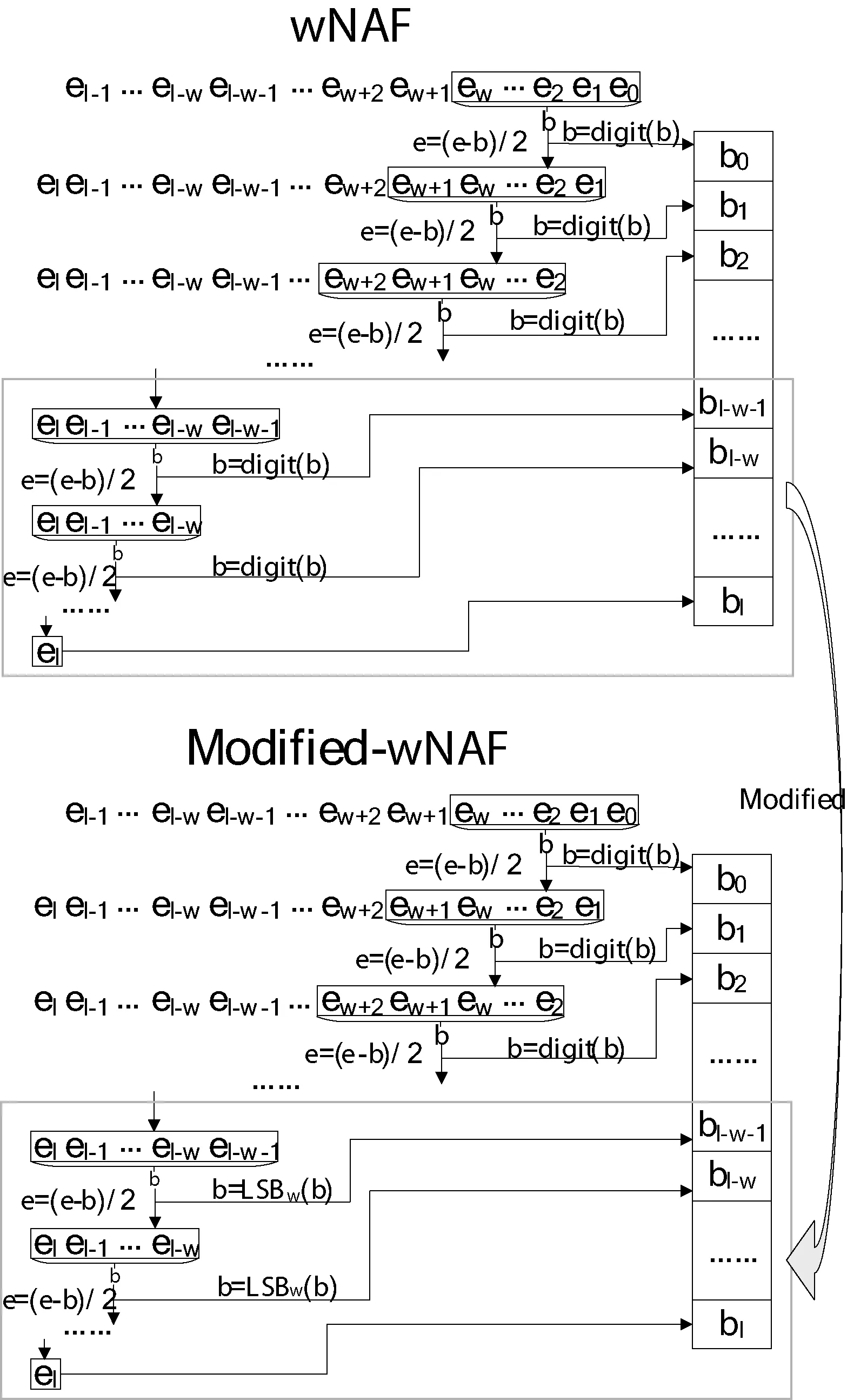
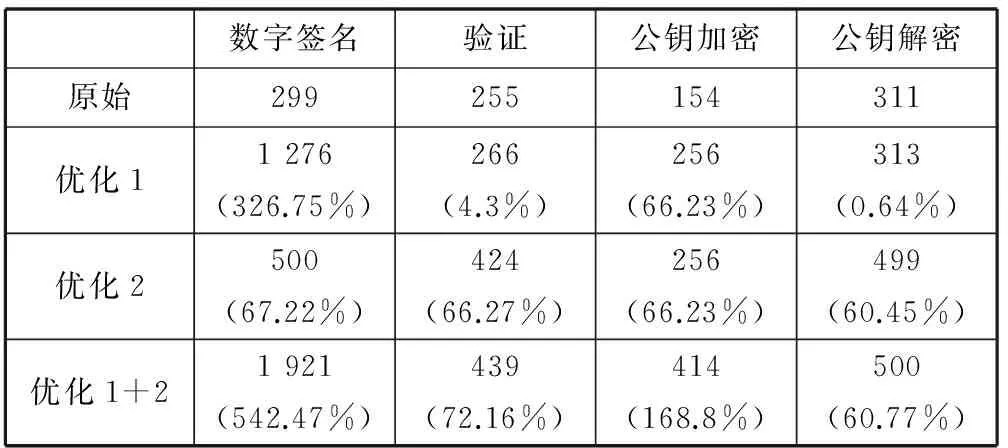
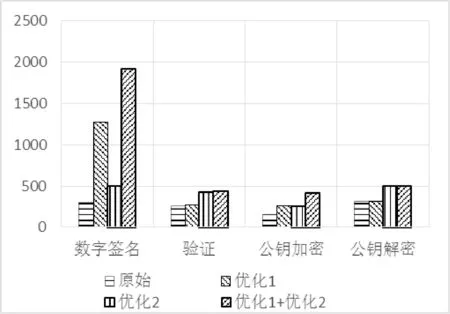
1: for i=0; i 2: C=0 3: for j=0; j 4: (C,S)=t[j]+A[j]*B[i]+C 5: t[j]=S 6: end for 7: (C,S)=t[s] +C 8: t[s]=S 9: t[s+1]=C 10: C=0 11: M=t[0]*N′[0] mod 2w 12: for j=0; j 13: (C,S)=t[j]+M*N[j] +C 14: t[j]=S 15: end for 16: (C,S)=t[s] +C 17: t[s]=S 18: t[s+1]= t[s+1]+C 19: end for 19: if(t>N) 20: t=t-N 21: end if 22: return t 由圖4可以看出,算法使用6個寄存器R0-R5存儲中間結果,B[i]A[0]+B[i]A[1]+B[i]A[2] +B[i]A[3]操作使用VMULU指令直接實現,這樣使用匯編語言直接實現的256位CIOS Montgomery模乘可以利用硬件大數乘加指令的優點,提高算法的性能。圖5是使用匯編程序實現256位CIOS算法的代碼,其中t2、t5寄存器用來加載乘數和被乘數,s0-s5用來存儲計算中間結果,最終得到的s0-s4是計算的最終結果被存儲到最終結果product中。 圖4 匯編實現256位CIOS算法結構 圖5 匯編程序實現256位CIOS算法的代碼 2.2 點加和倍點運算方法設計優化 對于點加和倍點運算,本文使用Jacobian投影坐標系[5]來進行計算,即投影點(X:Y:Z)與仿射點(X/Z2,Y/Z3)相對應,則橢圓曲線的方程轉化為: Y2Z=X3+aXZ4+bZ6 則點加的計算公式可以轉化為: (6) 倍點計算公式轉化為: (7) 由于國密SM2推薦曲線參數中: a= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC p= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF 即a=a-p=-3,則倍點公式可進一步優化為: (8) 下面我們分析使用仿射坐標系和Jacobian投影坐標系計算點加和倍點的復雜度,用M表示乘法運算,S表示平方運算,I表示求逆運算,加減法運算相對于乘法平方和求逆運算占用時間小,分析時忽略。根據Bernstein[8]實驗結果和分析知,如果選用域乘法效率不是特別低的情況下,I/M>8。這里假設S/M=0.8,I/M=8,分析點加和倍點運算復雜度如表2所示。 表2 不同坐標系下點加和倍點運算復雜度對比 測試OCTEON平臺上openssl軟件包中的BN_mod_mul(M), BN_mod_sqr(S), BN_mod_inverse(I)函數可知,OCTEON平臺上M、S、I三種操作使用時間對比為:S=0.9M,I=35M。 因此仿射坐標系下點加算法復雜度為:I+2M+S=37.9M,倍點為:I+2M+2S=38.8M;Jacobian投影坐標系下點加算法復雜度為:12M+4S=15.6M,倍點為:4M+4S=7.6M。由此可見使用Jacobian投影坐標后,點加和倍點的運算效率可得到顯著的提高。 2.3 點乘算法設計優化 SM2中用到的上層的點乘算法,主要分為兩種,一種是計算固定點的點乘:例如計算kG(G為橢圓曲線的基點);另一種是計算非固定點的點乘:例如計算lPA。對于點乘算法的優化,我們主要是參考Moller[9]提出的修改的wNAFs方法,對原始wNAF存在的問題進行分析,提出一種更易于實現的modified-wNAF方法。 下面先介紹原始的wNAF方法,使用窗口長度為w+1的NAF算法,將原來有{0,1}集合組成的二進制表示方式,轉化為由集合B={±1, ±3,…, ±(2w-1)}中的數組成的帶符號的wNAF方式。我們首先定義一個映射關系digit:{0,1,2,…,2w+1-1}->B∪{0}如下: (9) 下文中使用LSBm(c)表示取c最低m位,即LSBm(c)=cmod 2m。原始的窗口長度為w+1的NAF算法具體實現方法如圖6上半部分所示。這種算法采用從右至左的運算方式,取最低w+1位即b=LSBw+1(e),通過digit映射關系,將w+1位二進制數映射到集合B∪{0}中,則b=digit(b)即為最終結果b0;計算e=(e-b)/2,取最低w+1位并重復上述步驟計算出b1;按照此方式可以依次計算出b0至bl即為最終的wNAF表示。由于b-digit(b)=0或2w+1,故圖中求e=e-b=e-digit(b)的最低w位為0,e=(e-b)/2的最低w-1位為零。因此接下來求的(w-1)個bi為零,這就保證了wNAF表示中任何連續w個數字中最多1位為非零。 圖6 wNAF和modified-wNAF算法計算步驟對比 modified-wNAF方法實現方式如算法2所示,則計算點乘的窗口NAF方法見算法3。從算法3中可以看出需要計算iP,i∈{1, 3,…, (2w-1)},對于P點已知的情況iP可以通過預計算的方式,在程序開始之前計算完后存儲在預計算表中。當程序運行時直接查表讀取即可,這樣可以有效地節省程序的運行時間。因此SM2中在程序開始之前預計算基點G相關的點:G,3G,…,(2w-1)G并存在預計算表中供下面程序查詢使用,這樣可以大大提高接下來計算kG的效率。 算法2modified-wNAF算法 輸入:正整數e=(el-1,…,e1,e0),窗口長度w+1 輸出:b=modified-NAFw(e) =(bl,…,b1,b0) 1: c←e 2: i←0 3: while c>0 do 4: b←LSBw+1(c) 5: if (i+w+1)≥l && b≥2w 6: b←LSBw(b) 7: else 8: b←digit(b) 9: end if 10: c←c-b 11: bi←b 12: i←i+1 13: c←c/2 14: end while 15: return (bi-1,…,b1,b0) 算法3計算點乘的modified-wNAF算法 輸入:正整數k,窗口長度w+1,P∈E(Fq) 輸出:kP 1: modified-wNAF(k)= (kl-1,…, k1, k0) 2: for i∈{1, 3,…, 2w-1} do 3: Pi=iP 4: end for 5: Q←Ο 6: for i=l-1 to 0 do 7: Q←2Q 8: if ki>0 9: Q←Q+Pki 10: else if ki<0 11: Q←Q-Pki 12: end if 13: end for 14: return Q 2.4 優化方案安全性分析 在上述的優化方案中,最上層的點乘算法采用modified-wNAF算法。從算法3中可以看出:當ki≠0時,需要計算一次倍點和一次點加運算;而當ki=0時,僅需要計算一次倍點運算即可。攻擊者可以通過對能量曲線的分析,得到標量的哪些位為零。雖然不能直接破譯標量的值,但是對算法自身的安全性帶來嚴重的威脅。因此后續工作會展開對安全性的分析和優化。 本文在cavium公司的OCTEON CN6645平臺上[10]基于開源軟件庫openssl,實現了SM2數字簽名驗證及公鑰加解密算法。分別測試了在單核上運行優化前后數字簽名、驗證、公鑰加密、公鑰解密程序的執行速度(每秒能完成次數),測試結果如表3及圖7所示。優化1表示使用帶預計算的modified-wNAF方法,優化2表示使用大數乘加指令優化256位模乘算法。 表3 SM2各種算法優化前后速度對比(每秒執行次數) 圖7 SM2各種算法優化前后速度對比(每秒執行次數) 從實驗結果可以看出,優化2對于各種算法速度提高的百分比基本相同,大約在66%左右;而優化1對于各種算法速度提升的作用不盡相同。對于數字簽名這種主要操作是計算固定點點乘,優化1對于速度的提升是巨大的,能夠提升300%以上;對于公鑰解密這種計算非固定點點乘,優化1對于速度提升無影響;對于驗證和公鑰加密這種即需要計算非固定點又需要計算固定點點乘的算法,優化1能夠帶來一部分的速度提升。 總體來講,在OCTEON CN6645處理器上對國密SM2算法的整體優化,使得數字簽名速度提高了約為540%,驗證提高了約為72%,加密提高了169%,解密提高了61%。 本文提出了在OCTEON 處理器上實現SM2橢圓曲線密碼算法的整體優化方案,其重點就是對橢圓曲線上點乘算法進行優化。基于OCTEON處理器大數乘加指令和通用算法的優化,對點乘的實現算法從底層模運算,中間層點加倍點運算到最上層點乘運算逐層進行了優化。實驗結果表明:此種優化方案顯著提高了SM2算法的運算效率,SM2數字簽名效果最明顯,速度提高了約540%,每秒簽名次數由原來的299次提高到了1 920次。在提高算法效率的基礎上,算法的安全性也是需要重點考慮的問題。接下來的工作將會對算法的安全性進行優化,重點考慮抗SPA攻擊,使算法在保證效率的基礎上兼顧了安全特性。 [1] Koblitz N.Elliptic curve cryptosystems[J].Mathematics of computation,1987,48:203-209. [2] Miller V S.Use of Elliptic Curves in Cryptography[J].Lecture Notes in Computer Science,1986,218(1):417-426. [3] 國家密碼管理局.SM2橢圓曲線公鑰密碼算法[S/OL].[2010-12-17].http://www.oscca.gov.cn/News_1197.htm. [4] Cavium.OCTEON II CN66XX Multi-Core MIPS64 Processors[J/OL].[2011-07].http://www.cavium.com/OCTEON-II_CN66XX.html. [5] Hankerson D,Menezes A J,Vanstone S.Guide to elliptic curve cryptography[M].Springer,2004. [6] Montgomery P L.Modular multiplication without trial division[J].Mathematics of Computation,1985,44(170):519-521. [7] Koc C,Acar T,Kaliski B S.Analyzing and Comparing Montgomery Multiplication Algorithms[J].Micro IEEE,1996,16(3):26-33. [8] Bernstein D,Lange T.Analysis and optimization of elliptic-curve single-scalar multiplication[J].Contemporary Mathematics,2008. [9] M?ller B.Improved Techniques for Fast Exponentiation[C]//Information Security and Cryptology-Icisc 2002,International Conference Seoul,Korea,November 28-29,2002,Revised Papers,2002:298-312. [10] 李軍,陳君,倪宏,等.基于多核協作的流媒體內容緩存算法[J].網絡新媒體技術,2014,3(4):12-18. RESEARCHONWHOLEOPTIMIZATIONOFSM2PUBLICKEYCRYPTOGRAPHICIMPLEMENTATIONALGORITHMONOCTEONPROCESSOR Li Yang1,2Wang Jinlin1Zeng Xuewen1Ye Xiaozhou11 (NationalNetworkNewMediaEngineeringResearchCenter,InstituteofAcoustics,ChineseAcademyofSciences,Beijing100190,China)2(UniversityofChineseAcademyofSciences,Beijing100190,China) The core operation of SM2 elliptic curve public key cryptographic systems is point multiplication on elliptic curve. So, the key of efficient implementation of SM2 algorithm is to optimize the point multiplication. In this paper, we propose a whole optimization scheme to optimize the point multiplication from bottom to top. The top algorithm uses modified-wNAF with precomputation algorithm to compute point multiplication. The middle algorithm computes point adding and doubling with the Jacobian projected coordinate system. And the bottom algorithm optimizes the modular multiplication based on large multiply instructions on OCTEON platform. At last we implement the algorithms on OCTEON CN6645 and the experimental results show that SM2 signature, SM2 verify, SM2 encrypt and SM2 decrypt algorithms obtain increases by about 540%, 72%, 169% and 61% respectively. SM2 Elliptic curve cryptographic algorithm Point multiplication OCTEON processor TP309.7 A 10.3969/j.issn.1000-386x.2017.09.060 2016-10-11。中國科學院戰略性先導科技專項課題(XDA06010302);中國科學院聲學研究所知識創新工程項目(Y154191601)。李楊,博士生,主研領域:網絡安全。王勁林,研究員。曾學文,研究員。葉曉舟,研究員。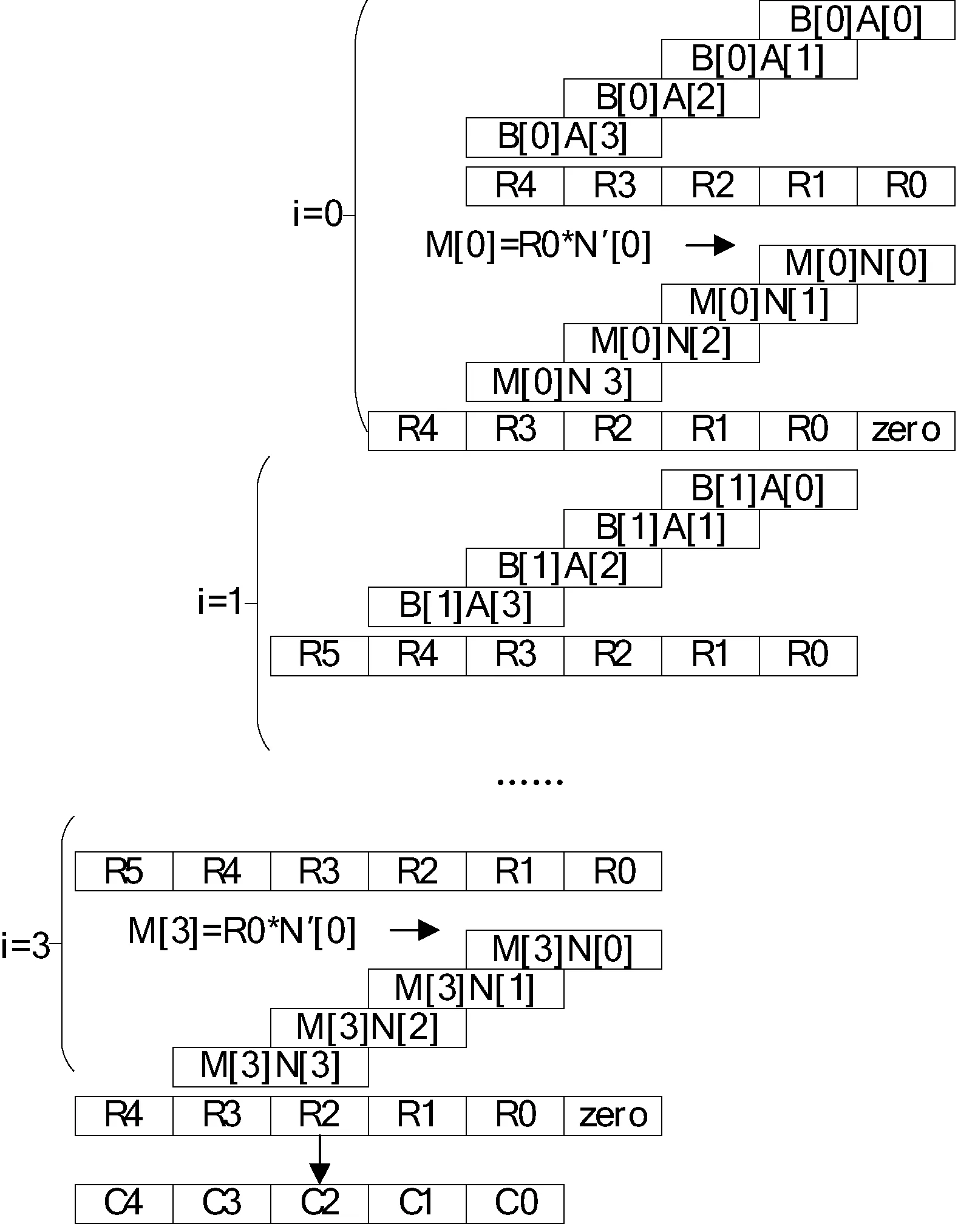

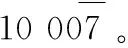
3 仿真實驗與結果分析
4 結 語

