基于概率統(tǒng)計模型傳感器資源管理算法

齊子薇 湖南大學統(tǒng)計學專業(yè)

1 引言

在對目標運動特性的描述上，既能用狀態(tài)空間來描述也能用概率統(tǒng)計的模型來描述，這兩種模型都是較為成熟的模型，且互相存在著緊密的聯(lián)系。在文獻中，可以看到在進行傳感器資源分配的時候，有的利用目標運動狀態(tài)的模型和信息增量的最大化來建立分配方法，也有的提出了在靜止的目標統(tǒng)計模型下方法。本文將綜合這兩種模型嘗試給出新的傳感器資源分配的方法，且在下文中闡述兩種模型所存在的必然的聯(lián)系。

2 概率密度的計算

信息增量最大化顧名思義就是在進行每一次的傳感器測量的時候，我們都將獲取最大的信息增量。信息增量就是信息熵的減少，因而可以使用目標出現(xiàn)概率密度來進行測量計算。在模型中，我們用表示目標運動的狀態(tài)的概率密度。在中x是在運動時刻t時，目標的向量，而Z表示的是到t時刻時目標的向量的集合。下文將對該密度進行深入的分析。

在一般情況下，狀態(tài)方程是一個連續(xù)的，量測方程是離散的。結(jié)合它們的特性我們將狀態(tài)方程公式定義為如下:

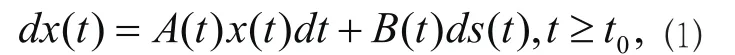
量測方程定義為：

公式（1）中，維度n狀態(tài)向量用X(t) 來表示A(t)、A(t)是表示在維度n×n和n×r的維度時變矩陣。其布朗運動過程為

公式（2）中z(k)是m維觀測向量，k和tk代表的是采樣數(shù)和采樣時刻，H(tk)是一個有界矩陣。其m維的白高斯序列為：

x(to)為初始條件，且為高斯分布，所以之間是沒有聯(lián)系的。

概率密度的變化主要有兩種情況：1、目標狀態(tài)轉(zhuǎn)移；2、對目標的量測時造成概率密度變化。本文將就這兩種情況進行概率密度的求取。

在傳感器得到量測后，概率密度的變化可以滿足貝葉斯規(guī)則，其公式如下：

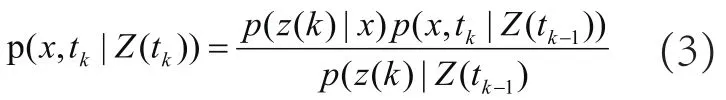
每一次的量測時似然函數(shù)為：

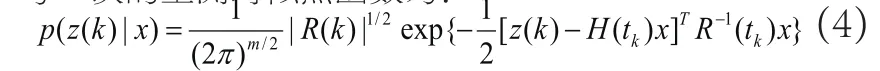
我們假定在公式（3）中概率分布為高斯分布就是：

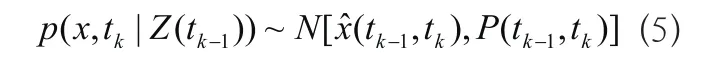
協(xié)方差為：

所以，

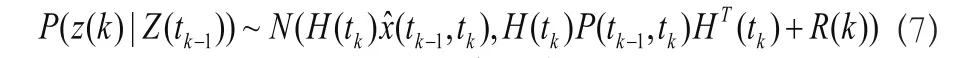
我們把上述的公式代入公式（2.18）則得出：

在這個公式中，

其中,

運動和量量測均為離散時，

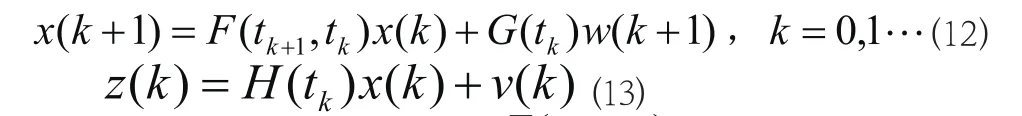
在量測更新時，如下:

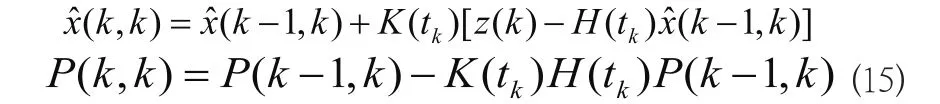
在量測更新的卡爾曼增益陣為：

我們可以利用上述的公式來求得狀態(tài)轉(zhuǎn)移和量測更新時的概率密度的變化，即由均值和協(xié)方差的變化來得到概率密度的變化。這些求值的方程正是卡爾曼濾波方程，因此，我們可得知兩種模型的結(jié)果是一致的。

3 傳感器分配原則

傳感器在進行分配的時候，其所遵循的規(guī)則是每一次的量測都會給予最大的信息增量。在量測時，概率密度的變化導致了信息增量，傳感器在調(diào)度時，不包含目標轉(zhuǎn)移所帶來的密度的變化，但是要注意兩者之間的關(guān)系。在一般情況來說，目標采樣的頻率沒有傳感器采樣快。我們假定傳感器的采樣率為f，我們就可以將目標的轉(zhuǎn)移率定為f/N。具體的方式為：在使用傳感器進行采樣時，在N次采樣時，其轉(zhuǎn)移概率不變；在有兩個或以上的N次采樣時，目標轉(zhuǎn)移概率發(fā)生的變化，轉(zhuǎn)移的初始概率是在采樣更新之后的概率。因此，最大信息增量就在”N次采樣“的基礎(chǔ)上進行的。

4 結(jié)論

本文以將目標狀態(tài)出現(xiàn)概率變化所產(chǎn)生的概率密度的變化分解成對應的均值與協(xié)方差的變化，在將兩種傳統(tǒng)的模型相結(jié)合給出了對運動目標檢測的傳感器管理辦法。

[1]武正江，趙明，鄧伊琴.一種新的無線傳感器網(wǎng)絡非均勻分簇雙簇頭算法——UDCH算法[J].小型微型計算機系統(tǒng)，2016，37(12):2612-2616.

[2]李孜，高春玲，孫澤宇，等.基于概率模型的無線傳感器網(wǎng)絡優(yōu)化覆蓋算法[J].光通信研究，2015，41(4):68-71.

[3]劉先省，周林，杜曉玉.基于RIMMKF的一種傳感器管理算法[J].電子學報，2007，35(12):2247-2251.

[4]徐松柏.基于跟蹤反饋的相控陣雷達宏微觀資源管理技術(shù)研究[D].杭州電子科技大學，2014.