船舶操縱非線性KT方程參數的辨識

鄭文龍，肖昌潤

(海軍工程大學 艦船工程系，湖北 武漢 430033)

船舶操縱非線性KT方程參數的辨識

鄭文龍，肖昌潤

(海軍工程大學 艦船工程系，湖北 武漢 430033)

利用差分進化法對一階和二階非線性船舶操縱KT方程中的參數進行辨識，采用積分的方法處理試驗數據以獲得辨識所需的樣本，將辨識結果與前人的方法進行比較，證明該方法能有效提高辨識精度。另外，辨識過程采用平行處理法代替分步辨識法，解決了辨識中的參數相消現象，同時也簡化了辨識流程。

船舶操縱KT方程；系統辨識；平行處理法

0 引 言

船舶操縱響應模型在船舶操縱性研究中占有重要地位。自野本謙作通過Z形試驗求取K，T的標準算法提出后[1]，各國的船舶操縱性研究者都樂于用Z形操舵試驗來確定K，T，以評價船舶的操縱性能。用系統辨識的方法來獲取K，T簡單、快速、準確。辛元歐等通過自然回歸離散模型的最小二乘法建立了一階和二階KT非線性的連續模型[2]；鄒早建等利用分步辨識的方法對一階和二階非線性KT方程的參數進行了辨識[3]；羅偉林結合船模自航模試驗，應用嶺回歸方法，辨識了一類非線性的船舶操縱運動數學模型并且進行了操縱運動預報[4]。文獻[2-3]在辨識時對原始數據采用差分的方法處理，誤差較大。本文利用積分方法獲取樣本數據，以使辨識的準確性有所提高。

1 系統辨識

系統辨識[5]是在系統的輸入和輸出數據基礎上，建立一個與所測系統等價的數學模型的理論和方法，包括確定模型結構和估計模型參數兩部分。系統辨識方法應用于船舶操縱運動建模已經有近40年的歷史。經典的辨識方法由于其本身的局限性已經逐漸被淘汰，智能算法因其對初值要求不高，不要求系統具有連續性等優勢而興起，差分進化法就是其中一種。

1.1 差分進化法簡介

Rainer Storn和Kenneth Price于1995年共同提出了一種基于群體進化的算法[6]，即差分進化法（Differential Evolution，DE），目的是求解切比雪夫多項式擬合問題。DE最大的特點就是可以記憶個體最優解并且在種群內共享信息，即利用群體內個體間的競爭與合作來求解優化問題，它基于實數進行編碼，具有保留精英個體的思想，實質是一種貪婪遺傳算法。整體結構上與其他進化算法類似，由變異、交叉和選擇3個基本操作構成。標準差分進化法主要包括4個步驟[7]。

1）生成初始群體

在n維空間里隨機生成滿足約束條件的M個個體，實施措施如下：

2）變異操作

如果無局部優化問題，變異操作可寫為

3）交叉操作

交叉操作是為了增加群體的多樣性，具體操作如下：

其中，rand lij為[0，1]之間的隨機小數；CR為交叉概率，CR∈[0，1]。

4）選擇操作

反復執行步驟2～步驟4操作，直到達到最大迭代次數G，差分進化基本運算流程如圖1所示。

1.2 參數相消現象及平行處理法

在辨識過程中，可能出現參數相消或者同時漂移現象[8]，使辨識的精度大大降低。因為，模型中每個方程可能包含多個參數，例如同時辨識2個參數A和B，由于計算中的最優化要求，A和B可能同時偏離真值，使得目標函數達到最小。克服參數相消是獲得較準確的辨識結果的基礎，分步辨識法和平行處理法[9]都可以有效抑制參數相消。文獻[3]運用了分步辨識的方法，但過程較為繁瑣，本文采用平行處理法，簡單而且有效。

Gelb（1974）年指出，系統所觀測到的信息越多，辨識的結果就越準確。所以增加觀測器無疑是一個好方法。如果選擇2個觀測器，它們互相獨立，如：

觀測器1

觀測器2

由無偏估計的要求，有

不妨設

那么

平行處理法不但可以提高參數辨識的精度，還可以改善參數相消現象。因為在平行處理過程中，要辨識的參數個數并沒有變化，但是所使用的數據卻并不相同，不同的數據對參數的辨識均做出貢獻，這樣對相互抵消有所抑制。在處理時，既可以2組不同的觀測數據，也可以用同一組觀測數據在不同相位條件下的值來進行參數平行處理辨識。

2 操縱運動響應方程

船舶在廣闊水域中航行，最關心的是航向問題，因此需要研究船舶的首向角對操舵的響應，這在自動操舵系統中尤為重要。一般的船舶首搖響應線性方程形式如下：

式（12）對分析航向穩定性很方便，也稱為二階線性KT方程。

1957年野本謙作用自動調節原理的方法，分析式（12）后提出了其簡化形式，在操作不是很頻繁的情況下，式（12）可近似用下式代替：

式（13）稱為一階KT方程，也稱作野本方程。系數K，T具有鮮明的物理意義：K為回轉性指數，能表征船舶回轉性能的好壞；T為應舵指數，表示轉首對操舵響應的快慢。式（13）在求解和分析問題時非常方便，所以得到了廣泛的應用。本文的待辨識參數即為一階和二階非線性操縱響應方程中K，α，T（T1，T2，T3）。

3 操縱運動響應方程的辨識

為了進行參數辨識，首先需要獲得樣本數據。從式（12）和式（13）中可以看出，在進行辨識時，除了用到首向角和舵角的數據外，還要用到首向角速度及其一、二次微分形式還有轉舵角速度，但是這些數據無法直接測得。文獻[2-3]均采用差分的方法，本文提出采用積分的方法，2種方法均可以獲得所需的樣本，不同的是，差分過程要在辨識前進行，而積分過程則在辨識過程中進行。

3.1 差分處理

在對數據進行差分處理時，一般采用的方法是向前差分格式，但其精度要低于中心差分[10]格式，因此這里以中心差分格式為說明，各階中心差分格式為：

文獻[3]中提出的分步辨識方法如下：

1）由小舵角回轉試驗辨識K；

2）固定K，由大舵角回轉試驗辨識α；

3）固定K和α，由大舵角Z形試驗辨識T（T1，T2，T3）；

4）用中舵角Z形試驗驗證辨識結果的準確性。

3.2 積分處理

對于一階非線性操縱響應方程，需進行如下計算：

對于二階非線性操縱響應方程，計算如下：

3.3 不同方法辨識結果的比較

本文所涉及的船模試驗包括一系列的回轉試驗和Z形試驗，積分法在不同工況下的辨識結果均要好于差分法。圖2是自航模試驗中10°/10°Z形運動首向角變化曲線，以此為例來對比二者的辨識結果。

分別用文獻[3]中的差分法和本文提出的積分法辨識一階和二階非線性響應方程中的參數，辨識結果如表1所示。

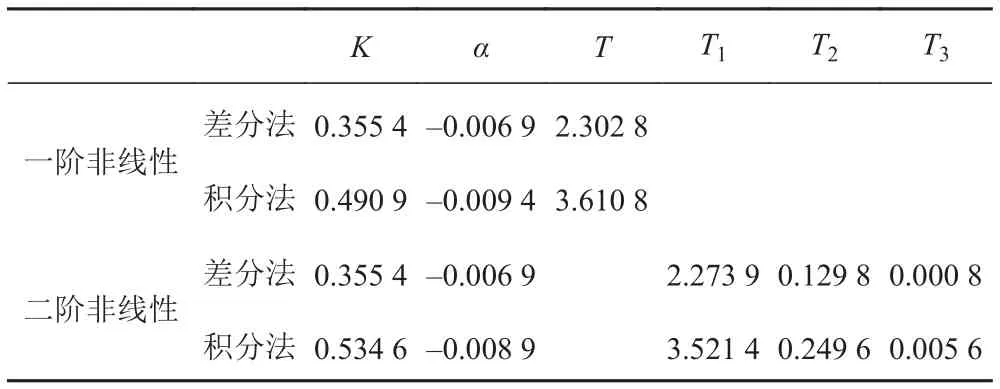
表 1 不同方法辨識結果Tab. 1 Identification results with different methods

為了驗證辨識結果的準確性，將以上結果帶到一階線性操縱響應方程中，模擬船舶10°/10°Z形運動，模擬結果如圖3所示。

從圖中可以看出，利用積分的方法獲得的樣本數據辨識的結果要遠好于通過差分方法得來的結果。

3.4 誤差分析

利用差分方法計算r時已經產生了一定的誤差，但是為了得到，等數據，又對差分后的結果進行差分，誤差逐漸積累，從而導致辨識結果的不準確。圖4用來比較分別用差分和積分的方法獲得的r，，。

從圖中可以看出，2種方法的差異在計算r時尚不明顯；但當計算時已經差別很大；計算時差異更加明顯。

4 結 語

本文改進了系統辨識過程中樣本數據的獲得途徑，變差分為積分，從而避免了差分過程造成的誤差。將辨識結果與差分處理的辨識結果以及野本手算法作比較，證明積分方法獲得的樣本數據更準確，能有效提高辨識精度。另外，在處理參數相消問題上采用平行處理法，可以一次辨識多個參數，簡化了辨識流程。

[1]NOMOTO K. On the steering qualities of ships[J]. International Shipbuilding Progress, 1957, 4(35).

[ 2 ]辛元歐, 俞勝芬. 關于KT方程類的辨識方法研究-自回歸模型的辨識[J]. 中國航海, 1983, 13(2): 28–43.XIN Yuan-ou, YU Sheng-fen. On the research of identification method forK-Ttype equations—identification of aitoregression modle[J]. Navigation of China, 1983, 13(2): 28–43.

[ 3 ]鄒早建, 吳秀恒. 船舶操縱性非線性KT方程參數的辨識[J].武漢理工大學學報(交通科學與工程版), 1985, 3: 001.ZOU Zao-jian, WU Xiu-heng. The parameter identification of non-linerK-Tequations on ship maneuverability[J]. Journal of Wuhan University of Technology(Transportation Science &Engineering) , 1985, 3: 001.

[ 4 ]羅偉林, 鄒早建. 基于嶺回歸方法的船舶操縱運動建模[J].船海工程, 2009, 38(6): 17–19.LUO Wei-lin, ZOU Zao-jian. Modeling of ship manoeuvring motion based on ridge regression[J]. Ship & Ocean Engineering, 2009, 38(6): 17–19.

[ 5 ]劉金琨, 沈曉蓉, 趙龍. 系統辨識理論及Matlab仿真[M]. 電子工業出版社, 2013.

[ 6 ]STORN R, PRICE K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4):341–359.

[ 7 ]楊啟文, 蔡亮, 薛云燦. 差分進化算法綜述[J]. 模式識別與人工智能, 2008, 21(4): 506–513.YANG Qi-wen, CAI Liang, XUE Yun-can. A survey of differential evolution algorithms[J]. PR&AR, 2008, 21(4):506–513.

[ 8 ]吳秀恒, 劉祖源, 施生達. 船舶操縱性[M]. 北京: 國防工業出版社, 2005.

[ 9 ]STOLFO S J. Parallel processing method: U. S. Patent 4, 843,540[P]. 1989-6-27.

[10]李常青, 樓夢麟. 中心-偏心差分法[J]. 同濟大學學報(自然科學版), 2011, 02: 179–186.LI Chang-qing, LOU Meng-lin. Central-eccentric difference method[J]. Journal of Tongji University(Natural Science),2011, 02: 179–186.

The parameter identification ofKTequations on ship maneuverability

ZHENG Wen-long, XIAO Chang-run
(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

Identified the parameters of the first and second order ship maneuvering nolinear response equation. Itegrated the test datas to get sample datas. It has been confirmed that this method can improve the accuracy of identification compared to other methods. Using the parallel processing method, instead of step-by-step identification to reduce parameters offset. This method can also simplify identification flow.

KTequations on ship maneuverability；system identification；the parallel processing method

U661.3

A

1672 – 7649(2017)09 – 0129 – 04

10.3404/j.issn.1672 – 7649.2017.09.025

2016 – 08 – 12；

2016 – 09 – 12

鄭文龍(1991 – )，男，碩士研究生，研究方向為艦船流體力學。