遺傳與粒子群算法在閉環(huán)混合系統(tǒng)運作中的應(yīng)用

王心月　郭健全

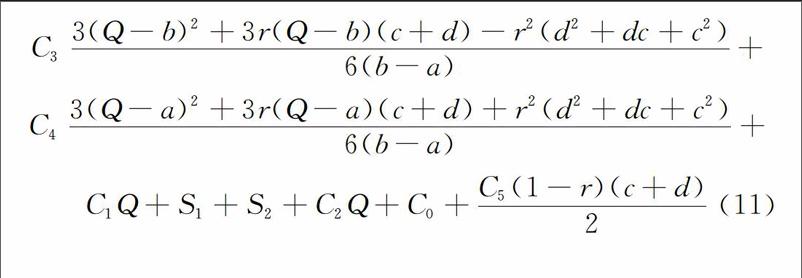
摘 要：設(shè)計需求和再制造率不確定情況下的制造/再制造系統(tǒng)的最優(yōu)回收及生產(chǎn)策略模型，并通過具體算例，采用遺傳算法（GA）和粒子群算法（PSO）求解，對比驗證模型的信度和效度。仿真結(jié)果表明，兩種算法既可靈活獲得多種情況下的系統(tǒng)最優(yōu)運作策略，又能反映制造數(shù)量和回收品質(zhì)量水平在不同再制造率下的變化規(guī)律，可為企業(yè)在多重不確定下降低總成本提供參考。

關(guān)鍵詞：隨機需求；隨機再制造率；閉環(huán)混合系統(tǒng)；GA&PSO

DOI：10.11907/rjdk.172073

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2017）009-0034-04

Abstract：The optimal recycling and production strategy model based on random demand and yield is investigated in a closed-loop hybrid manufacturing/remanufacturing system. A numerical example is used to verify the validity and credibility of the model by adopting genetic algorithm （GA） and particle swarm optimization （PSO） algorithm. The results show that it is applicable for GA and PSO to solve the optimal operation strategy according to different situations and the variations of manufacturing quantity and the quality level of the returned items under the different remanufacturing rate are presented. A reference could be provided for minimizing the total cost of the system in view of multiple uncertainties.

Key Words：random demand； random yield； closed-loop hybrid system； GA&PSO

0 引言

近年來環(huán)境問題日益突出，再制造成為節(jié)能減排和提高資源利用率的有效方式[1]。再制造作為閉環(huán)供應(yīng)鏈的重要組成部分，其回收品的數(shù)量、市場需求和再制造率等一系列未知因素加大了生產(chǎn)計劃的難度[2]。Han等[3]提出優(yōu)化模型解決不確定需求下的混合制造/再制造定價問題，并對不確定參數(shù)進行敏感性分析。Shi等[4]假設(shè)需求和回收存在不確定性，建立利潤最大化模型來研究供應(yīng)鏈的生產(chǎn)計劃。Pokharel和Liang[5]研究回收品被隨機用于再制造的最優(yōu)回收定價及回收數(shù)量問題。以上研究較少考慮再制造率的隨機性，以及未能在多重不確定環(huán)境下研究回收與生產(chǎn)決策。

在再制造生產(chǎn)計劃問題中，較多采用遺傳算法、蟻群算法、模擬退火、粒子群算法等單一智能算法，雖然其效果顯著，但每種算法都有各自的局限性。鑒于此，區(qū)別于以往單一算法的局限性，在多重不確定下的閉環(huán)混合制造/再制造系統(tǒng)最優(yōu)回收及生產(chǎn)計劃中，采用粒子群和遺傳兩種算法，對具體實例對比驗證求解，既避免粒子群算法陷入局部最優(yōu)，又避免遺傳算法搜索速度的局限性，更具有可靠性和互補性。

1 數(shù)學(xué)規(guī)劃模型

混合制造/再制造系統(tǒng)如圖1所示，包含制造品和再制造品組成的可用庫存、回收品庫存及原材料庫存3部分。制造商回收舊產(chǎn)品，同時生產(chǎn)制造品和再制造品，且兩種產(chǎn)品質(zhì)量無差異，共同滿足市場需求。

1.1 模型假設(shè)

作如下假設(shè)：①回收品質(zhì)量水平服從指數(shù)分布[6]；②回收成本、再制造成本是關(guān)于回收品質(zhì)量水平的負指數(shù)函數(shù)[7]；③再制造品和新產(chǎn)品質(zhì)量無差異[8]；④不考慮提前期[9]；⑤需求服從均勻分布，M∈（a，b），b>a，a>0；回收品數(shù)量服從均勻分布，N∈（c，d），d>c，c>0[10]。

1.2 函數(shù)構(gòu)建

1.2.1 回收成本函數(shù)

定義回收品最佳質(zhì)量水平為q（0≤q≤1），q服從指數(shù)分布，q～E（λ）， x為回收品質(zhì)量水平（q≤x≤1），λ為指數(shù)分布參數(shù)。其概率密度函數(shù)為X（x）=λe—λx，q

0，其它。

其中，w為慣性權(quán)重，其影響上次迭代過程中粒子在此次迭代過程中速度的大小。c1、c2為加速度常數(shù)，c1代表粒子自身的認知學(xué)習(xí)能力，是粒子對比自身最優(yōu)適應(yīng)度值的慣性權(quán)重系數(shù)。c2代表整個粒子群體認知的能力，是粒子參照種群最優(yōu)適應(yīng)度值的慣性權(quán)重數(shù)。r1、r2是一組隨機數(shù)，分布在[0，1]區(qū)間內(nèi)。限定粒子的速度vin∈[-Vmaxn，Vmaxn]，以免粒子在搜索過程中超出所定義的空間。

粒子群算法的主要編寫步驟如下：

步驟1：設(shè)定粒子群規(guī)模為N，隨機初始化粒子位置及速度信息，本文初始化回收品質(zhì)量水平q，再制造率r和制造數(shù)量Q。

步驟2：根據(jù)適應(yīng)度函數(shù)（11）獲得所有粒子的適應(yīng)度值大小。

步驟3：比較歷史適應(yīng)度值，若當前適應(yīng)度值較優(yōu)，則記為Pbest；比較群體最優(yōu)適應(yīng)度值，若當前適應(yīng)度值較優(yōu)，則記為gbest。

步驟4：根據(jù)進化方程（12）-（14）對粒子位置和速度持續(xù)更新。

步驟5：若滿足終止規(guī)則，終止程序并輸出最優(yōu)解，否則轉(zhuǎn)向步驟2。

2.2 遺傳算法

遺傳算法（GA）是一種模擬生物演化過程的智能搜索算法，具有魯棒性、并行性等特點，被廣泛用于求解復(fù)雜優(yōu)化問題[12]。因此，本文同時選用遺傳算法對比驗證解決多目標優(yōu)化問題。

遺傳算法的主要步驟如下：

步驟1：初始化。隨機產(chǎn)生由若干個個體組成的一個初始種群，如圖2所示。

步驟2：適應(yīng)度評估。適應(yīng)度直接反映個體的優(yōu)劣程度，個體適應(yīng)度值用適應(yīng)度函數(shù)f（x）=1 000/objvalue（11）來評估計算。

步驟3：選擇。選擇的目的是提高全局收斂性及效率，使適應(yīng)度值較大的個體有機會成為父代，個體被選擇的概率為p（x）=f（x）/∑f（x）。

步驟4：交叉與變異。交叉：使新一代繼承父代的特性，并具有高于父代的適應(yīng)性，從而保證全局搜索能力。一個交叉算子如圖3所示。變異：以較小概率隨機改變某個個體的基因值，形成的新個體保證了種群的多樣性。

步驟5：終止條件。若到達預(yù)設(shè)的最大迭代次數(shù)，終止算法，否則轉(zhuǎn)向步驟2。

3 模型求解

為驗證模型和算法的有效性，采取具體實例驗證。已知h1=0.2，h2=1，h3=0.2，C1=10，C2=5，C3=12，C4=4，C5=3，CO=800，S1=1 000，S2=1 000，a=1 000，b=1 300，c=200，d=850，l=0.9，k=0.9，γ=0.1，β=0.9，φ=2，λ=1。對于不同的θ（回收成本函數(shù)參數(shù)）和δ（再制造成本函數(shù)參數(shù)），PSO和GA分別求得的最優(yōu)策略如表1所示，GAP值=（PSO-GA）/GA。以θ=4，δ=1為例，兩種算法計算的不同再制造率下的最優(yōu)回收及生產(chǎn)方案，如圖4—圖6所示。

表1表明：①兩種算法都可求出最優(yōu)解，即驗證了模型的有效性；②兩種算法的GAP值最大是0.003%，即表明解未陷入局部最優(yōu)，進一步驗證了模型的可信度；③當δ保持不變時，隨著θ逐漸增大，Q逐漸增大，q逐漸減小，逐漸減小，ATC逐漸增大。即企業(yè)通過降低回收品最佳質(zhì)量水平來盡可能降低回收成本，再制造率因回收品質(zhì)量水平的下降而下降，進而制造數(shù)量因再制造數(shù)量的下降而升高；④當θ保持不變時，隨著δ逐漸增大，Q逐漸增大，q逐漸增大，r逐漸增大，ATC逐漸增大。即企業(yè)通過提高回收品最佳質(zhì)量水平來盡可能降低再制造成本，再制造率r也因回收品質(zhì)量水平的上升而上升，進而制造數(shù)量因再制造數(shù)量的上升而下降；⑤PSO和GA計算結(jié)果與事實相符合，可以合理解釋模型的經(jīng)濟意義，即驗證了兩種算法求解混合系統(tǒng)運作策略具有較高的應(yīng)用價值。

由圖4—圖6可得到以下結(jié)論：①隨著r逐漸增大，Q逐漸減小，q逐漸增大，即隨著再制造率的上升，可用于再制造的回收品數(shù)量上升，因此制造品數(shù)量逐漸下降，回收品質(zhì)量水平隨著再制造率的上升呈現(xiàn)上升趨勢；②由PSO和GA兩種算法計算出的ATC變化趨勢可看出，兩種算法變化趨勢一致，且結(jié)果差值較小，可見該模型可信度較高，同時也驗證了兩種算法解決該問題的合理性，更具有說服力。

4 結(jié)語

在不確定需求、不確定再制造率和不確定質(zhì)量下建立閉環(huán)混合系統(tǒng)的最優(yōu)回收及生產(chǎn)決策模型，并采用GA算法和PSO算法對比驗證模型的可信性和有效性。實驗表明，兩種算法能規(guī)避單一算法的局限性，較好解決混合系統(tǒng)的生產(chǎn)計劃問題。

參考文獻：

[1] WANG Y， CHANG X， CHEN Z， et al. Impact of subsidy policies on recycling and remanufacturing using system dynamics methodology： a case of auto parts in China[J]. Journal of Cleaner Production，2014，74（7）：161-171.

[2] WANG J， ZHAO J， WANG X. Optimum policy in hybrid manufacturing/remanufacturing system[J].Computers & Industrial Engineering，2011，60（3）：411-419.

[3] HAN S， MA W， ZHAO L， et al. A robust optimisation model for hybrid remanufacturing and manufacturing systems under uncertain return quality and market demand[J].International Journal of Production Research，2016，54（17）：5056-5072.

[4] SHI J， ZHANG G， SHA J. Optimal production and pricing policy for a closed loop system[J]. Resources， Conservation and Recycling，2011，55（6）：639-647.

[5] POKHAREL S， LIANG Y. A model to evaluate acquisition price and quantity of used products for remanufacturing[J]. International Journal of Production Economics，2012，138（1）：170-176.

[6] GUO J， YA G. Optimal strategies for manufacturing/remanufacturing system with the consideration of recycled products[J]. Computers & Industrial Engineering， 2015，89：226-234.endprint

[7] Vrs J. Product Balancing under conditions of quality inflation， cost pressures and growth strategies[J]. European Journal of Operational Research，2002，141（1）：153-166.

[8] ARAS N， VERTER V， BOYACI T. Coordination and priority decisions in hybrid manufacturing/remanufacturing systems[J]. Production and Operations Management，2006，15（4）：528-543.

[9] WANG X， GUO J， LIANG C. Optimal strategies for a closed-loop hybrid system with supply disruption in e-commerce environment[C]. 2016 IEEE 13th International Conference on e-Business Engineering （ICEBE），2016：299-304.

[10] GIRI B C， SHARMA S. Optimal production policy for a closed-loop hybrid system with uncertain demand and return under supply disruption[J]. Journal of Cleaner Production，2016，112：2015-2028.

[11] ORESKI S， ORESKI G. Genetic algorithm-based heuristic for feature selection in credit risk assessment[J].Expert systems with applications，2014，41（4）：2052-2064.

[12] HAO J X， YU Y， LAW R， et al. A genetic algorithm-based learning approach to understand customer satisfaction with OTA websites[J]. Tourism Management，2015，48：231-241.

（責(zé)任編輯：孫 娟）endprint