一種并行差分隱私關聯規則挖掘算法

申澤宇　袁健

摘 要：針對傳統基于ε-差分隱私模型的top-k關聯規則挖掘算法在大規模數據環境下挖掘效率低下的問題，提出了一種并行差分隱私關聯規則挖掘算法。算法利用Hadoop框架實現并行計算，利用負載均衡策略，使每一個節點分配到的數據量相當，利用指數機制挑選出k個頻繁模式，采用拉普拉斯機制對這k個頻繁模式添加噪音。通過實驗對算法的頻繁模式挖掘結果與同類算法進行比較分析，結果表明，該算法在保證挖掘結果具有可用性的前提下，在效率上較傳統算法有所提升。

關鍵詞：頻繁模式挖掘；差分隱私；指數機制；并行計算

DOI：10.11907/rjdk.171559

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2017）009-0065-03

Abstract：In order to solve the problem of low efficiency of mining Top-k Association Rules Mining Algorithm Based on the differential privacy model in large scale data environment， a parallel algorithm for mining association rules based on differential privacy is proposed. The algorithm using Hadoop framework to realize parallel computing using the load balancing strategy， the amount of data so that each node is assigned to a selected K， using the index mechanism of frequent pattern， using the Laplasse mechanism add noise to these K frequent pattern. The results of the algorithm are compared with other algorithms. The experimental results show that the proposed algorithm can improve the efficiency of the mining algorithm than the traditional algorithm.

Key Words：frequent pattern mining； differential privacy； exponential mechanism； parallel computing

0 引言

隨著大數據時代的到來，數據挖掘成為研究熱點。而關聯規則挖掘是數據挖掘中的一個重要研究課題。關聯規則挖掘能夠從數據中挖掘出潛在的項目之間的隱藏關系，如應用醫療數據挖掘疾病之間的關聯，利用用戶交易數據挖掘用戶購買行為之間的關聯等。然而對原始數據的發布會造成個人隱私泄漏，頻繁模式挖掘是關聯規則挖掘的核心，傳統的頻繁模式挖掘算法在面對海量數據時占用內存大、效率低。如何提高算法效率和數據的可用性，同時解決隱私保護問題成為關聯規則分析的一個熱點。鑒于此，提出一種并行差分隱私頻繁模式挖掘算法。

1 相關工作

目前，在差分隱私模型下對頻繁模式挖掘進行研究并取得了一定的研究成果。文獻[1]利用指數機制選取支持度最大的k個模式，對其添加噪聲得到top-k頻繁模式。文獻[2]利用θ-基以及映射技術提出了PrivBasis算法，首先由θ-頻繁對構建出候選集合，接著對候選集合的頻度添加噪聲，最后選取k個作為top-k頻繁模式。文獻[3]考慮事務長度對全局敏感度的影響，提出智能截斷和雙重標準，有效提升了結果的可用性，但該方法只限于短事務居多的事務數據集。文獻[4]利用指數機制從候選集中選取top-k頻繁模式，并對選取的頻繁模式進行噪音擾動，而后通過對結果進行二次規劃，提升數據的可用性。目前，關于差分隱私頻繁模式挖掘的研究雖已取得一定成果，但相關算法仍存在著消耗內存大、效率低的問題。文獻[5-13]提出了并行頻繁模式挖掘算法，利用Hadoop平臺的多個節點并行運算算法，可以有效地實施并行化，但仍會產生大量候選項集，且當數據量大于數十萬數量級時算法無法高效率運行。針對這一問題，本文提出基于指數機制和帶負載均衡的分布式FP-growth算法的分布式差分隱私頻繁模式挖掘算法（Parallel Differential Privacy Frequent Pattern Mining Algorithm，PDPFPM），擬在保證挖掘結果可用的前提下提升頻繁模式挖掘效率，滿足大數據的需求。通過與同類算法進行比較，驗證了PDPFPM算法的可行性和有效性。

2 相關定義

2.1 差分隱私

定義1（鄰近數據集）：若數據集D1和D2有且僅有一條數據項的值不同，則稱D1和D2為鄰近數據集。

定義2（差分隱私）：給定隱私保護算法f，若f對鄰近數據集D1和D2的輸出結果O∈Range（f）均滿足下列不等式，則稱算法f滿足ε-差分隱私。Pr[f（T1∈0）]≤eε×Pr[f（T2∈0）]

（1） 其中，ε為隱私預算，衡量差分隱私保護的水平。由式（1）可知ε越小，隱私保護的水平越強。f是一個隨機的算法，Range（f）表示算法f的取值范圍。Pr[f（T∈0）]表示輸出f（T）結果為O的概率。

定義3（全局敏感度）：對于任意的查詢函數q：D→Rd，函數q的全局敏感度為：Sq=max‖q（D1）·q（D2）‖endprint

（2） 其中，D1和D2是兄弟數據集，R表示所對應的實數空間，d表示查詢q的查詢維度，q（Di）表示查詢函數q在數據集Di上的查詢結果。

定理1（串行組合定理）：給定一組隨機算法f={f1，f2，…，fn}，每個算法fi均在數據集T上實現了εi-差分隱私，其中i=1，2，…，n，則該組隨機算法f在數據集T上實現了∑ni=1εi-差分隱私。

2.2 噪聲機制

定義4（拉普拉斯機制）：通過對數據添加服從拉普拉斯分布的噪聲，實現差分隱私保護。其基本思想是對數據集D進行查詢q，查詢結果為q（D）。向q（D）添加噪聲χ，其中χ是一個滿足拉普拉斯分布的連續型隨機變量，其概率密度函數為：Pr[χ]=12be|x-μ|b

（3） μ為期望，在差分隱私算法中一般μ取0，方差為2b2，b用來衡量添加噪聲的大小。對于給定的查詢函數q：D→Rd，若算法f的輸出結果滿足式（3），則算法f滿足ε-差分隱私。f（D）=q（D）+〈Lap1（sqε），…，Lapd（sqε）〉

（4） 其中，Lapd（sqε）是相互獨立的拉普拉斯噪聲，拉普拉斯參數b=Sq/ε。

2.3 指數機制

定義5（指數機制[15]）：對于給定的一個評價函數u：（D×0）→R，若算法f滿足等式（5），則算法f滿足ε-差分隱私。f（D，u）={r：Pr[r∈0]}∝exp（εu（D，r）Δu）

（5） 其中，r表示輸出項，Pr（r∈0）表示r輸出的概率，Δu為評價函數u的全局敏感度。其關鍵在于設計一個評價函數u，通過u得到輸出結果集O中r的指數分布，r被選擇輸出的概率服從式（5）的概率分布。

3 并行差分隱私頻繁模式挖掘算法

PDPFPM可以有效解決在海量數據下，運用FP-Growth算法進行頻繁模式挖掘時，占用內存過多、效率低的不足，克服了MPI并行編程模型存在的節點失效、網絡通信故障等缺點，同時在挖掘出頻繁模式時，可以保護其支持度計數不被泄漏。

3.1 基本思想

首先，統計事務數據庫中每一個項的支持度并找出所有頻繁項，得到頻繁F1項集（FList）；其次進行計算量估計，Map 過程采用根據計算量估計的分割方式讀入事務項，分發到不同的Reduce 節點。Reduce 過程對構造的FP-Tree 進行FP-Growth 挖掘得到局部頻繁項集，再由指數機制Pr[c]=exp（ε1×c×r2×n）∑ni=0exp（ε1×ci×r2×n）選出n個頻繁模式，對所選出的支持度計數添加拉普拉斯噪音，最后由局部頻繁項集合并成全局頻繁項集，選取支持度最高的n個。

3.2 基于計算量估計的分組策略

整個并行FP-Growth的計算量主要在于各節點的頻繁模式的數量，而一般支持度高的項，其計算量較大。SSCE設定每項的估計計算量為C=∑ri=0Ci，其中r為每條數據的含有項集。將傳入數據集前P個數據r的每一項作為一組，P為節點數，計算每一組的計算量，將下一條數據加入到最小的一組，重復計算直到整個數據集遍歷完畢。

3.3 算法描述及流程

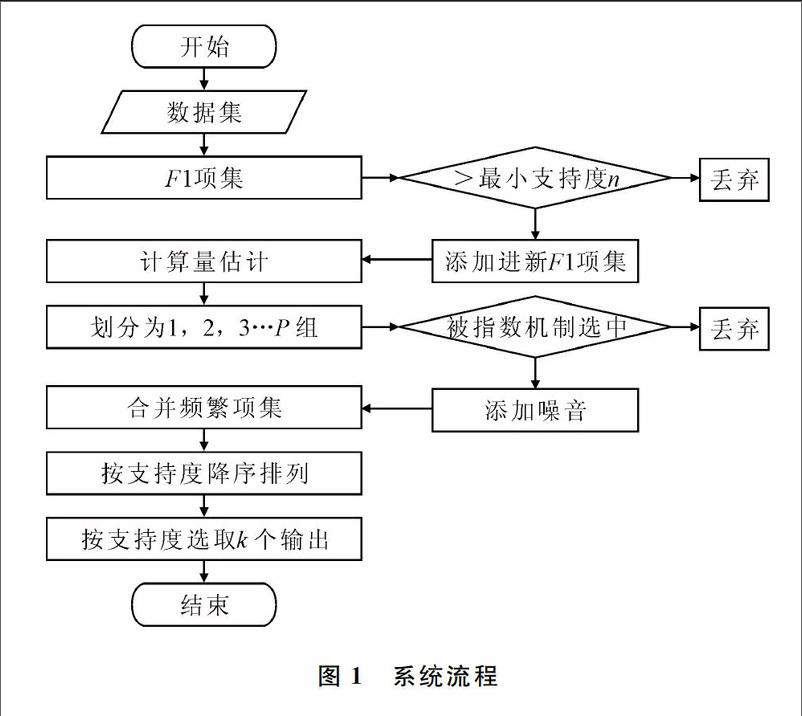
PDPFPM算法流程如圖1所示。

步驟1：掃描數據集，統計頻繁F1項集（FList）。Map過程：第一次全量掃描數據，計算出各自候選F1項集。Reduce過程：收集Map 階段輸出的中間結果，進行求和，統計每項在整個數據源中的支持度，舍棄小于最小支持度的項，得到FList并按支持度降序排列。

步驟2：計算量估計，進行數據劃分。Map過程：第二次全量地訪問數據集，遍歷每條數據中的項，按SSCE分成P個組輸出的key值為分組號p，value為去除小于最小支持度的子項集。Combiner過程：聚合每組中的數據，形成待處理的數據。

步驟3：添加噪音，進行隱私保護。此為加噪以及挖掘的一步，整個步驟為一個Reduce過程。建立FP-Tree，然后通過FP-Growth挖掘算法得到頻繁項集，采用指數機制選出n個頻繁模式，對其支持度添加Lap（kε2）噪音。

步驟4：局部頻繁項集合并成全局頻繁項集。讀取HDFS 文件中的結果，相同局部頻繁項集的支持度求和，得到全局支持度。按支持度降序排列，選擇前n個保存，作為最后的全局頻繁項集。

4 實驗設計與分析

本文從數據可用性和算法性能的角度對PDPFPM算法進行分析，并與傳統的頻繁模式隱私保護算法進行比較。采用算法耗時來對算法性能進行衡量，采用準確率和召回率的調和平均值（F-score）對數據的可用性進行衡量，由于算法添加噪音具有隨機性，取10次實驗的平均值。

定義5（F-score） 設Rp為隱私保護后的挖掘結果，Ra為準確的挖掘結果。準確率（Precision）表示挖掘出的準確結果，召回率（Recall）表示準確結果被挖掘出的概率，由定義可以看出，準確率和召回率是一對互斥的標準，采用F-score將兩者結合，F-score值越大，數據的可用性越高。Precision=Rp∩RaRp

（5）

recall=Rp∩RaRa

（6）

F-score=2×precision×recallprecision+recall

（7）4.1 實驗設置

實驗采用IBM研究團隊開發的數據生成器生成T10I4D100K數據集，對PDPFPM算法的數據可用性和算法性能進行分析。

4.2 實驗結果分析

隱私預算ε1和ε2各取0.5，計算F-score的取值，與DP-topkP[4]相比發現PDPFPM算法F-score的值比DP-topkP有所下降，這主要是由于分布式處理時，各單節點添加的噪音造成噪音積累，因此造成了F-score的下降，實驗結果如表2所示。endprint

通過實驗驗證算法的性能，實驗結果如表3所示（時間單位：s）。可以發現，PDPFPM算法處理時間提升同時隱私保護水平相當。

頻繁模式挖掘的隱私保護日益成為大數據分析的基礎之一，頻繁模式挖掘受到了大量數據分析者的青睞，針對傳統基于ε-差分隱私模型的top-k關聯規則挖掘算法在大規模數據環境下挖掘效率低下的問題，提出PDPFPM算法，實驗表明其可以有效解決算法的性能問題。

參考文獻：

[1] BHASKAR R， LAXMAN S， SMITH A， et al. Discovering frequent patterns in sensitive data[C].Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，ACM，2010：503-512.

[2] LI N， QARDAJI W， SU D， et al. PrivBasis：frequent itemset mining with differential privacy[J].Proceedings of the Vldb Endowment，2012，5（11）：1340-1351.

[3] ZENG C， NAUGHTON J F， CAI J Y. On differentially private frequent itemset mining[J]. Proceedings of the Vldb Endowment，2012，6（1）：25-36.

[4] ZHANG X， WANG M， MENG X.An accurate method for mining top-k frequent pattern under differential privacy[J]. Journal of Computer Research & Development，2014，51（1）：104-114.

[5] FANG M，SHIVAKUMAR N，GARCIA-MOLINA H，et al.Computing iceberg queries efficiently[C].Proceedings of the 24rd International Conference on Very Large Data Bases. Morgan Kaufmann Publishers Inc.，2000：299-310.

[6] QURESHI Z，BANSAL J，BANSAL S.A survey on association rule mining in cloud computing[J]. International Journal of Emerging Technology and Advanced Engineering，2013，3（4）：2250-2459.

[7] ASHRAFI M Z， TANIAR D， SMITH K.ODAM： An optimized distributed association rule mining algorithm[J]. Distributed Systems Online IEEE，2004，5（3）：1.

[8] LI L，ZHANG M.The Strategy of mining association rule based on cloud computing[C].International Conference on Business Computing and Global Informatization.IEEE Computer Society，2011：475-478.

[9] SANJEEV R， GUPTA P. Implementing improved algorithm over apriori data mining association rule algorithm[J]. IJCST，2012，3（1）：2250-2459.

[10] CHEN S Y， LI J H， LIN K C， et al.Using MapReduce framework for mining association rules[M]. Information Technology Convergence. Springer Netherlands，2013：723-731.

[11] RIONDATO M， DEBRABANT J A， FONSECA R， et al. PARMA：a parallel randomized algorithm for approximate association rules mining in MapReduce[C].ACM International Conference on Information and Knowledge Management，2012：85-94.

[12] YANG X Y， LIU Z， FU Y. MapReduce as a programming model for association rules algorithm on Hadoop[C]. International Conference on Information Sciences and Interaction Sciences，2010：99-102.

[13] LI N， ZENG L， HE Q， et al. Parallel implementation of apriori algorithm based on MapReduce[C]. Acis International Conference on Software Engineering， Artificial Intelligence，NETWORKING and Parallel & Distributed Computing，2012：236-241.

（責任編輯：孫 娟）endprint