基于并行編程模型的SPECK 2n算法實現與優化

◆程雨芊

（山東大學（威海）網絡與信息管理中心 山東 264200）

基于并行編程模型的SPECK 2n算法實現與優化

◆程雨芊

（山東大學（威海）網絡與信息管理中心 山東 264200）

SPECK 2n算法是一種典型的輕量級分組密碼算法，具有較強的靈活性和安全性，廣泛應用于數據加密，以保證數據的完整性和可靠性。為了應對大數據的加密，本文提出一種基于 MPI+OpenMP的混合并行編程模型，可以充分利用分布式存儲模型和共享存儲模型的特點來優化加密過程，并基于山東大學（威海）超級計算中心集群進行測試。實驗結果表明，優化后的并行SPECK 2n算法達到了較高的加速比，能夠有效處理大數據量的實時加密，極大地提高了計算效率。

并行編程；密碼算法；分布式存儲模型；共享存儲模型

0 引言

SPECK 2n系列密碼算法是由美國國家安全局（NSA）設計，在 2013年發布的具有 Feistel結構的輕量級分組密碼算法[1]。SPECK系列分組密碼算法的分組長度為32、48、64、96或128比特，密鑰長度為64、72、96、128、144、192或256比特，即分組長度和密鑰長度可變，有利于在不同的軟件平臺上實現，具有很強的應用靈活性。同時 SPECK算法有較強的安全性，雖然針對 SPECK系列密碼算法已經有了一些安全性分析結果，如Farzaneh Abed等人提出的飛去來器攻擊和矩形攻擊[2]、Alex Biryukov等人提出的差分攻擊[3]以及由Itai Dinur改進的差分攻擊[4]等，但目前還沒有全輪數的SPECK算法安全性分析。

在大數據快速發展的形勢下，如何保證大數據的安全性和可靠性，是很多數據型企業所關心的問題。SPECK 2n算法作為輕量級的分組密碼算法，主要用于對數據的快速實時加密，對加密的效率有一定的要求，因此并行化的SPECK 2n算法實現逐漸受到重視。

高性能計算作為一個新興科學，致力于研究高效能的并行計算，對于科學實驗模擬計算和大數據分析等起到了推動作用。利用高性能計算可以提高計算效率，節約時間和資源，滿足大數據環境下的計算需求。高性能計算的實現方式主要有兩種，一種是充分利用CPU本身的資源進行并行計算，如OpenMP多線程并行、MPI多進程并行等；另一種是利用加速卡進行輔助計算，如NVIDIA公司的GPU加速卡和Intel公司的MIC加速卡等。

本文提出一種基于MPI+OpenMP并行編程模型的SPECK 2n算法實現，將待加密的明文數據進行分塊，然后使用MPI進程并行和OpenMP線程并行嵌套完成加密算法。經實驗驗證，將多進程并行與多線程并行結合起來的層次化并行方法能夠取得較好的加密效率。

1 并行編程模型介紹

并行編程模型根據內存模型的不同，主要分為共享存儲模型和分布式存儲模型兩種。共享存儲的并行編程模型具有單一內存地址、易編程、可擴展性較差等特點，適合中小規模的計算，主要實現的方式有OpenMP、PThread、X3H5等；分布式存儲的并行編程模型又稱為消息傳遞模型，具有地址空間獨立、編程復雜、可擴展性較好等特點，適合大規模的并行計算，主要的實現方式有MPI、PVM等。消息傳遞模型與多線程編程模型組合而成的混合編程模型更適用于大數據環境下的多層次、可擴展的并行算法[5-6]。

MPI消息傳遞模型適合并行計算粒度大的算法，要求用戶適當地分解計算數據，不同的節點之間可以進行靈活地進行數據交換。MPI主要使用函數接口實現并行環境初始化以及消息傳遞等功能。OpenMP多線程編程模型適合細粒度的并行算法，利用編譯指導語句#pragma實現線程的Fork-Join以及參量的屬性設置，共享的內存可以避免不必要的數據交換，提高算法的執行效率。因此 MPI+OpenMP并行編程模型能夠同時結合分布式存儲和共享存儲的優勢，充分利用計算集群的節點間和節點內的兩級并行來進行算法實現。

2 SPECK 2n算法

2.1 SPECK 2n算法介紹

SPECK 2n系列密碼算法是由Ray Beaulieu等人在2013年提出的一種輕量級分組密碼算法，密鑰長度和分組長度均不固定，可以根據具體的安全性要求、性能要求以及應用環境等來選擇合適的分組長度和密鑰長度。SPECK 2n系列密碼算法的十個典型實例算法如表1，其中n表示字長，單位為比特（bit），m表示主密鑰的字數，α和β表示循環移位的參量，T為加密的輪數；分組長度即為輸入明文和輸出密文的比特數，密鑰長度為主密鑰的比特數，α、β和T是加密算法函數中的參數。

表1 SPECK 2n算法的參數設置

SPECK 2n算法主要包括兩個部分：加密主函數和密鑰擴展函數。加密主函數用來進行明文的加密操作，輸出相應的密文；密鑰擴展函數將輸入的主密鑰擴展成T個輪密鑰，用于主函數運算。加密主函數由T輪的輪函數組成，SPECK 2n算法的輪函數主要由循環移位操作、異或運算和域上的模加運算組成，第i輪加密函數為：

其中Xi和Yi是第i輪加密的輸入分組，Xi+1和Yi+1是第i輪加密的輸出分組，Ki表示第i輪的子密鑰，長度均為n比特；>>>和<<<表示按比特位的循環右移和循環左移，表示域上的加法運⊕算， 表示按比特位的異或操作。

SPECK 2n系列密碼算法的密鑰擴展函數利用輪函數來生成輪密鑰，輸入為主密鑰輸出為T個輪密鑰用于每一輪的加密運算。對于所有的計算ki和li的公式如下：

2.2 并行SPECK 2n算法的基本原理

根據SPECK 2n算法的輪函數結構可以看出，SPECK 2n算法先將數據進行分塊，然后每個數據塊分別進行對應輪數的加密計算，除了對密鑰擴展函數、主密鑰和輪密鑰比特進行讀取外，各個數據塊間的加密操作互不影響，加密順序也無依賴性。因此，對于密鑰相同的待加密數據，可以進行節點內的并行加密運算；對于密鑰不同的待加密數據，可以進行節點間的并行加密運算。

3 基于并行編程模型的SPECK 2n算法

單機環境下，串行的SPECK 2n算法主要采用迭代方式實現，多次讀取更新密鑰比特來進行不同密鑰的明文數據的加密計算。算法計算的核心內容是輪函數的實現，對于所有明文數據分組，進行T輪的計算，得到密文數據分組。本文采用MPI分布式存儲模型優化數據分塊和輪函數，進而再結合OpenMP共享存儲模型進一步改進SPECK算法。

3.1 基于MPI的并行SPECK 2n算法

根據SPECK 2n算法輪函數的特點，基于MPI的并行SPECK算法實現主要對輸入數據進行分塊處理，由主進程進行整體的邏輯控制，開啟多個進程并發執行每個數據分組的輪函數計算。相同密鑰的數據加密算法分為兩個部分：第一部分是根據主密鑰生成輪密鑰，第二部分是使用輪密鑰進行數據加密。每一部分數據加密完成后，要將明文和密文數據對應輸出到文件，以便于進行算法結果的驗證。

3.2 基于MPI+OpenMP的并行SPECK 2n算法

在上述基于MPI并行的SPECK 2n算法的基礎之上，當同一密鑰加密的數據量很大時，可以構建基于MPI和OpenMP的混合編程模型，同時實現多進程和多線程的編程。每個MPI進程內部發散出多個線程，同時對多個數據分組進行重復的輪函數運算，可以極大地提高計算效率。

計算數據分塊的主要依據是加密所使用的密鑰和SPECK 2n實例算法的字長等參量，對于不同密鑰加密的數據，可以采用MPI多進程并行的方式；對于同一密鑰加密的數據，可以采用OpenMP多線程并行，減少密鑰交換次數和密鑰擴展函數的使用次數。

4 測試環境與結果分析

4.1 測試環境介紹

山東大學（威海）超級計算中心集群采用 CPU+GPU+MIC 的三重異構架構，計算節點+胖節點混合的體系結構。配置了1臺管理節點和1臺登錄節點。計算資源包括34臺CPU計算節點、1臺胖節點、2臺GPU節點和2臺MIC節點。集群總計856個CPU計算核心，CPU的計算能力為32Tflops（每秒計算32萬億次）， 2臺GPU節點計算能力為4.6Tflops，2臺MIC節點計算能力為4.8Tflops。集群使用了全互連無阻塞的Infiniband 56Gb FDR高速計算網絡和千兆的高速管理和監控網絡。采用了lustre并行文件系統，并行存儲裸容量為200TB。

在此計算平臺上，使用 CPU計算節點進行實驗測試。每個CPU節點包含1個Intel(R) Xeon(R) CPU E5-2660 v3 @ 2.60GHz處理器（20個邏輯CPU），操作系統版本為Red Hat Enterprise Linux Server release 6.5，已配置好MPI和OpenMP的并行環境，編譯器為icpc version 15.0.1和impi 5.0.2.044，程序采用C++語言編寫，每個節點啟動一個MPI進程，每個MPI進程在OpenMP并行區域內最多啟用8個OpenMP線程組。

4.2 測試結果與分析

通過對串行算法（SPECK）、基于 MPI的并行算法（MPI-SPECK）、基于 MPI+OpenMP的并行算法（MPI/OpenMP-SPECK）三種算法實現的性能進行比較，來分析多層次并行加密計算的優勢和效率。

實驗確定以SPECK 32/64算法為例進行測試分析，對應的參量α和β值為7和2，輪數T為22，選取了三組不同的輸入明文數據量，分別為2MB、32MB和512MB，每組進行7種實驗，使用的CPU節點數目為單節點、4節點和8節點，實驗的詳細說明如表2所列：

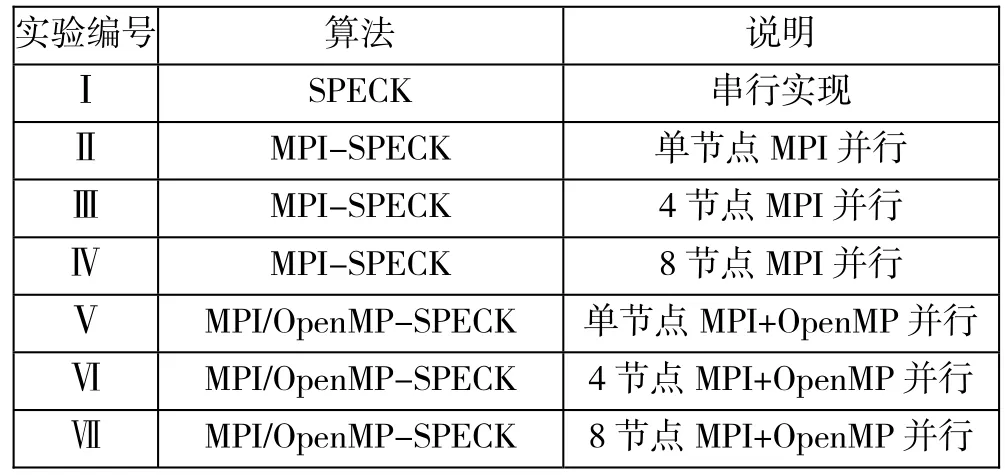
表2 實驗詳細說明

實驗對算法運行時間進行了記錄，結果如表3所列。

表3 算法運行時間（單位：s）

加速比是衡量算法并行化性能和效果的標準，加速比指的是同一個算法在單處理器系統和并行處理器系統中運行所消耗的時間的比率。根據表3列出的運行時間，可以計算出三種數據量對應的不同編程模型的加速比，結果如圖1所示。

對不同數據量的明文進行加密測試實驗表明，并行編程的加速比優勢十分明顯。從圖1可以看出，基于MPI并行模型的計算時間較基于MIP+OpenMP混合并行模型的計算時間略高，這是由于算法實現中存在部分共享常量，使用OpenMP多線程并行可以避免不必要的數據交換，提高執行效率。

圖1 運行時間的加速比

5 結束語

本文實現了基于MPI+OpenMP的并行SPECK 2n算法，并通過多種實驗驗證，基于混合編程模型的算法實現具有較高的加速比，能夠充分結合分布式存儲和共享存儲的優勢，提高計算效率。但同時層次化的并行編程模型也存在著一些問題，比如OpenMP線程在 Fork-Join時產生的系統開銷問題、MPI進程間的數據傳輸優化問題等。最后，感謝山東大學（威海）超級計算中心的計算支持和幫助。

[1]Ray Beaulieu, Douglas Shors, Jason Smith, etc. The SIMON and SPECK Families of Lightweight Block Ciphers[R].Cryptology ePrint Archive, 2013, Report 2013/404:http://eprint.iacr.org/.

[2]Farzaneh Abed, Eik List, Jakob Wenzel, etc. Differential Cryptanalysis of round-reduced Simon and Speck[R]. Fast Software Encryption，2015.

[3]Alex Biryukov, Arnab Roy, and Vesselin Velichkov.Differential Analysis of Block Ciphers SIMON and SPECK[R].Fast Software Encryption，2015.

[4]Itai Dinur. Improved Differential Cryptanalysis of Round-Reduced Speck[R]. Selected Areas in Cryptography-SAC 2014.

[5]唐兵,Laurent BOBELIN,賀海武.基于 MPI和 OpenMP混合編程的非負矩陣分解并行算法[J].計算機科學，2017.

[6]馮云,周淑秋.MPI+OpenMP混合并行編程模型應用研究[J].計算機系統應用，2006.

[7]宋鵬，解闖，李金山等.基于 MPI+OpenMP的三維聲波方程正演模擬[J].中國海洋大學學報自然科學版，2015.

[8]周文.基于眾核架構的 BP神經網絡算法優化[J].電子世界，2017.