船舶電力系統無功優化的GSA-IPM算法
唐卓貞
?
船舶電力系統無功優化的GSA-IPM算法
唐卓貞
(南通航運職業技術學院,江蘇南通 226010 )
提出GSA-IPM(萬有引力-內點)算法求解船舶電力系統無功優化問題,以降低船舶電力系統的有功損耗,提高電壓質量,改善安全經濟運行水平。將算法應用于某實際船舶電力系統進行仿真測試,結果與萬有引力搜索算法(GSA)、遺傳算法(GA)及粒子群算法(PSO)作比較,證明了算法能夠使有功網損更低,電壓質量更佳,從而驗證了方法的有效性。
船舶工程 船舶電力系統 無功優化 GSA-IPM算法
0 引言
大規模大容量的電力系統在船舶工業領域不斷得到應用,以及在船舶電力系統的特殊地位,其安全穩定性至關重要。為了改善船舶電力系統的經濟安全運行狀況,降低系統有功損耗,改善電能的質量,進一步開展無功優化的分析、研究顯得日益迫切。
船舶電力系統無功優化問題是包含多個變量、約束的混合非線性規劃問題,求解這類問題有智能算法[1]與數值算法[2]兩類。前者較擅于處理連續性優化問題,但在處理離散變量時具有明顯不足。后者對于離散變量的處理顯著優于前者,但易陷于局部最優解。萬有引力搜索算法(GSA)[3,4]作為新近提出的啟發式算法,已被證明較其它同類算法具有更好的魯棒性,并能取得更佳的優化結果,而現代內點法(IPM)則以求解大規模非線性規劃問題著稱。
結合GSA與IPM提出了一種求解船舶電力系統無功優化的新型混合算法,并對所建立的船舶電力系統無功優化模型進行了求解。
1 船舶電力系統無功優化
1.1 電力系統無功優化
無功優化問題是一個含有多變量(離散與連續)、多約束(發電機機端電壓、變壓器分接頭的調節以及電容器組的投切)的復雜非線性規劃問題。
無功優化的數學表示如下:
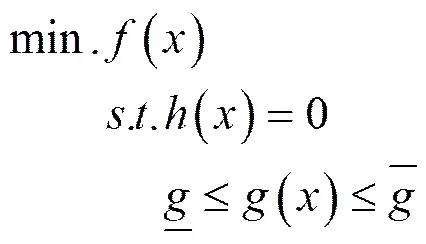
1.2 船舶電力系統無功優化
船舶電力系統是孤立系統,與陸上電力系統有諸多差異,如輸電方式、系統容量和負荷類型等,船舶電站供給的負荷通常分為船舶用電設備的負荷(動力用電、生活用電)與其它功率損耗(線路阻抗等功率損耗)兩部分。其中的無功負荷主要是電動機的感性負載。
船舶電力系統無功優化數學模型可表述如下。
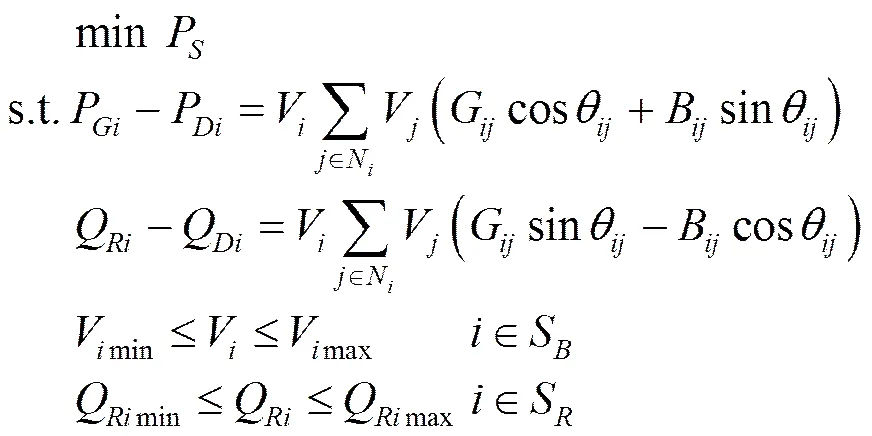
2 GSA-IPM算法
2.1 萬有引力算法原理
萬有引力搜索算法于2009年由Rashedi等人提出,該算法是受牛頓萬有引力定律和運動定律的啟發。該算法認為,任何粒子間均以萬有引力相互作用,該作用力使所有粒子趨向于質量更大的粒子運動。由此,更重的粒子的適應度值更高,它的位置即對應于更優解。
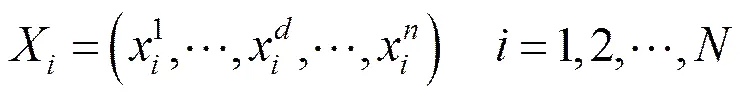
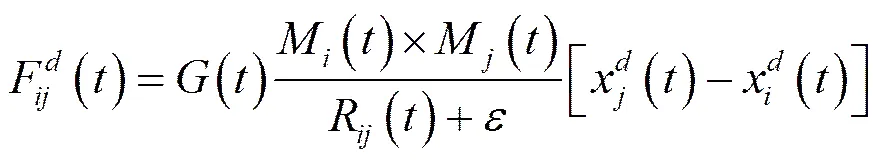
(5)
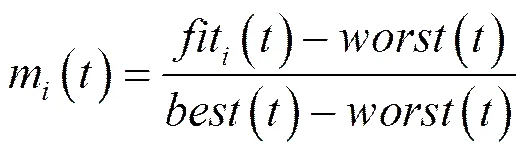
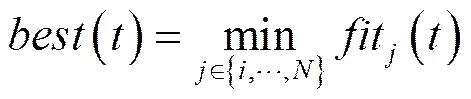
(8)
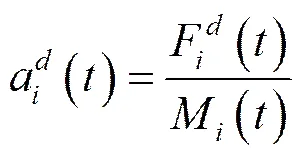
(10)
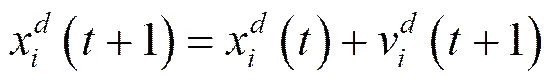
2.2 現代內點算法原理
H. Wei等人于2000年將現代內點算法應用于求解大規模水火最優潮流問題,取得了重要成果[5]。該算法考慮如式(1)描述的規劃問題。先引入松馳變量對該問題進行等價變換:
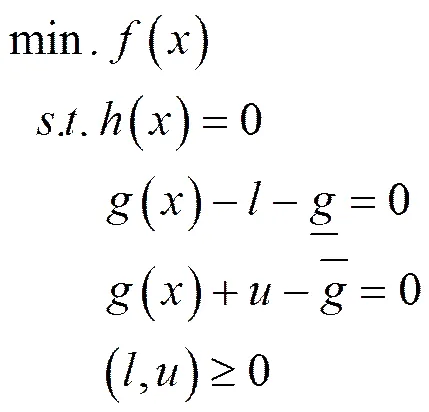
再構建一個拉格朗日函數。
(13)
得到KKT方程。
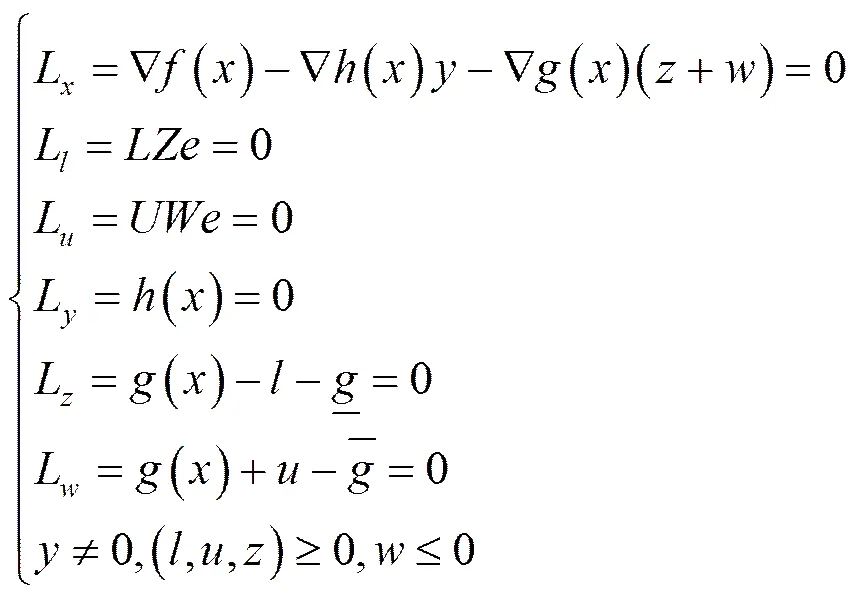
2.3 GSA-IPM混合算法
2.3.1 算法思路
以GSA算法為代表的隨機方法,在處理離散問題上比較適合,但易陷入局部最優。以IPM為代表的確定性方法,雖在連續優化問題上有優勢,但不適合處理離散變量。結合GSA與IPM的優點,提出一種GSA-IPM混合算法來求解無功優化。
首先采用GSA對離散變量進行初始化,計算其適應度。在潮流計算中用IPM對連續變量進行優化,優化結果再與GSA的結果交互迭代,再計算其適應度。對各個個體的目標函數值作排序,優秀個體替代次優個體參與下一輪迭代,直到找到最優解或迭代終止。
2.3.2 算法流程
GSA-IPM算法的流程見圖1。
注:普通潮流網損(p.u.)為0.719
3 算例分析
為驗證上述算法和模型的有效性,對某實際的船舶電力系統[2]進行仿真測試,所有數據都采用標幺值,電壓約束是[1, 1.1],無功出力約束是[-50, 50]。計算機配置條件為:Intel i5 CPU 4.21 GHz,4 GB內存,Windows 7 Professional,Matlab R2012a。
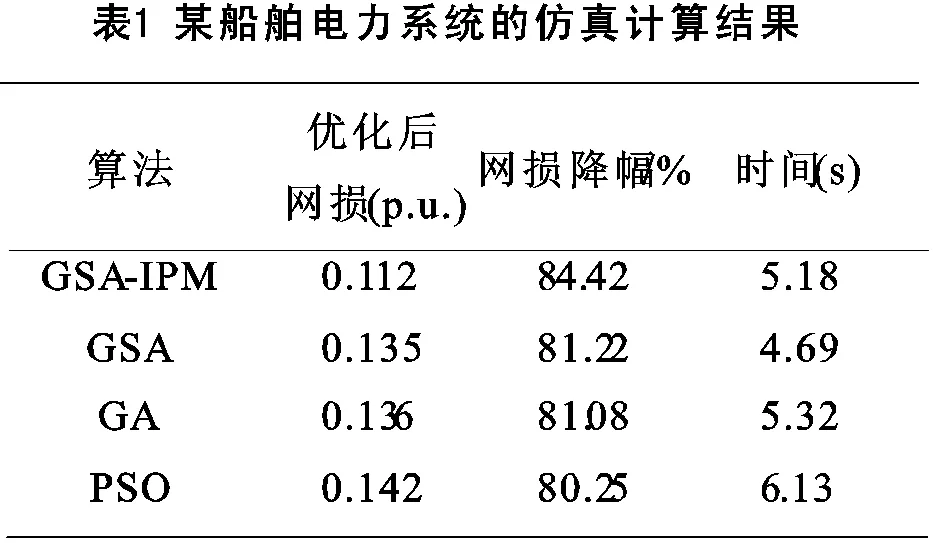
為了驗證提出的GSA-IPM算法在求解船舶電力系統無功優化問題上的效果,分別利用GSA-IPM、GSA、GA和PSO這4種算法在相同條件下求解,其結果如表1所示。
由表1可見,萬有引力算法能將該船舶電力系統的有功損耗優化得更低,由于采用了GSA與IPM的混合優化方法,其計算時間略長于單純使用GSA算法。表2給出了初始潮流及GSA-IPM優化結果,所有電壓都得到優化。
4 結論
1)提出的GSA-IPM算法適用于求解多目標、多變量、多約束的混合非線性規劃問題。
2)通過對某實際船舶電力系統進行仿真測試,結果驗證了所提算法和模型的正確性、有效性。
3)GSA-IPM算法船舶電力系統無功優化運行方法能改善系統的安全經濟運行水平,具有更為優越的效益。
[1] 李彥, 董龍龍, 雍建容, 等. 基于改進粒子群算法的艦船電力系統無功優化[J]. 中國航海, 2014, 37(4): 30-33, 39.
[2] 唐卓貞, 沈蘇海, 薛斌. 基于現代內點法的船舶電力系統無功優化[J]. 中國航海, 2010,33(3):36-38.
[3] Rashedi, E., Nezamabadi-pour, H., Saryazdi, S. GSA: a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232–2248.
[4] S. Duman Y. Sonmez U. Guvenc, et al. Optimal reactive power dispatch using a gravitational search algorithm [J]. IET Gener. Transm. Distrib., 2012, 6(6): 1044–1051.
[5] H. Wei, H. Sasaki, J. Kubokawa, et al. Large scale hydro-thermal optimal power flow problems based on interior point nonlinear programming[J]. IEEE Transactions On Power Systems, 2000, 15(1): 396-403.
GSA-IPM Algorithm of Reactive Power Optimization for Ship’s Power System
Tang Zhuozhen
( Nantong Shipping College, Nantong 226010, Jiangsu, China )
TM7
A
1003-4862(2017)03-0009-04
2016-09-15
唐卓貞(1984-),女,碩士,講師。研究方向:船舶電力系統。

