考慮時序與儲能配合的分布式電源優化配置研究

陳聰偉 江修波 劉麗軍

?

考慮時序與儲能配合的分布式電源優化配置研究

陳聰偉1江修波2劉麗軍2

（福州大學電氣工程與自動化學院，福州 350116）

本文基于不同類型負荷和DG的典型時序特性，以及考慮不同類型污染物的環境代價和儲能效益，以配電網年社會成本、年購電成本、年環境成本、年可靠性成本、最低點電壓偏移量為目標函數，建立DG和儲能設備的優化配置模型。該模型根據負荷和DG出力的時序性，對DG和儲能裝置的位置和容量進行協同優化。同時為了改善NSGA-II初始化多樣性低、交叉變異概率恒定、收斂速度慢等缺點，將云模型的思想融入到NSGA-II中，并利用改進的云模型NSGA-II對上述模型進行尋優，然后再用1—9標度法與隸屬度函數相結合的方法對尋優的結果進行評價。最后，通過IEEE-33節點系統對該模型進行仿真。結果表明，上述模型和算法能有效地對分布式電源和儲能設備進行優化配置。

儲能裝置；云模型；NSGA-II算法；時序特性；分布式電源

隨著我國經濟發展，電力需求日益增長，煤、石油、天然氣等傳統化石能源過度使用造成環境污染問題日趨嚴重，因此安裝具有線損低、清潔環保、效率高、發電方式靈活的DG受到人們越來越多的青睞。我國自然資源種類多，擁有豐富的風能，水能和光能資源，這為DG的發展奠定了基礎。

但是風力發電和光伏發電出力具有波動性，如果大規模接入DG，就會造成整個配電網不穩定，可能出現雙向潮流和局部節點電壓過高的現象，因此配電網對DG的接納能力受到嚴格限制。雖然風力發電和光伏發電出力在時序上具有互補的特性，但是綜合考慮負荷的時序性，僅安裝這兩種分布式電源是不能完全平抑DG波動的，因此本文研究在接入DG的同時，也適量安裝一定的儲能裝置，根據DG出力和負荷的時序特性，實時調整儲能裝置的充放電狀態，盡可能使DG出力的波動性降到最低，這能夠大大提升配電網對DG的接納能力。因此，如何合理配置DG和儲能裝置的位置和容量以使目標函數達到最優，成為國內外專家學者研究的熱點之一。

文獻[1-2]在負荷需求水平和DG出力恒定的前提下對DG進行選址定容優化配置，并未考慮負荷和DG出力的時序性與實際情況相差較大的問題。文獻[3]考慮了DG出力和負荷的時序特性，同時也提及了儲能裝置，但未根據三者的實際運行情況對其進行協同優化。文獻[4]的模型中只提及風力發電的波動性，沒有充分考慮負荷需求的波動性。文獻[5]以線路有功損耗和電壓穩定性作為目標函數，但在求解過程中將其轉化為單目標求解。文獻[6]充分考慮風力發電，光伏發電和負荷的時序特性，并以年碳排放量最小建立DG的優化配置模型，但是該模型未考慮儲能裝置。文獻[7]充分考慮DG和負荷的時序特性并對儲能裝置進行協同規劃，但未考慮儲能裝置的效益、政府補貼、節點電壓質量等因素，其模型還不夠全面，同時該模型未對算法進行改進，求解的算法仍存在不足。上述文獻從不同角度研究DG的優化配置，建立考慮不同指標的數學模型。本文在前人研究的基礎上，取其精華并對其不足進行補充和修正，建立充分考慮DG、儲能裝置和負荷的時序特性以及儲能效益的多目標分布式電源優化配置模型，并采用基于云模型的NSGA-II對上述模型進行求解，最后采用1—9標度法與隸屬度函數相結合的方法對尋優的結果進行評價。

1 考慮時序與儲能配合的DG優化配置數學模型

本文以風力發電，光伏發電和儲能裝置為研究對象，基于負荷和DG出力的時序性建立以年社會成本、年購電成本、年環境成本、年可靠性成本和最低點電壓偏移量最小的多目標分布式電源優化配置模型，具體如式（1）、式（2）所示：

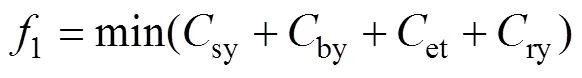
（2）

1.1 年社會成本

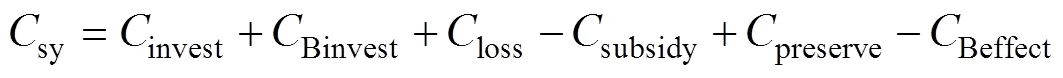
其中

（4）

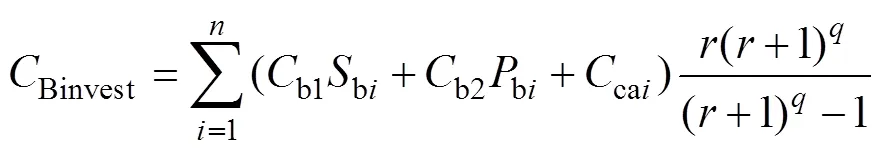
（6）

（7）

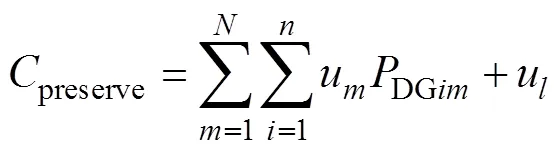
（9）

1.2 年購電成本

年購電成本的大小能夠反映一個地區的負荷密度以及該地區接納分布式電源的能力，具體模型為

1.3 年環境成本

年環鏡成本可以有效反映一個地區使用傳統發電廠發電的比例，年環境成本越高表明該地區利用傳統火電廠的電能越多，本文根據碳氧化物和二氧化硫的排放強度確定環境成本具體表達式如下：

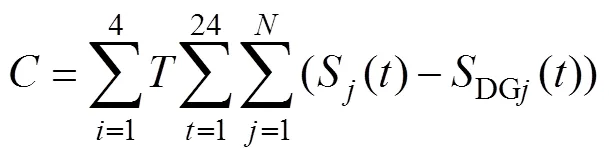
（12）

1.4 年可靠性成本

DG并網可以有效改變配電網的運行方式，使單電源供電的輻射狀網絡轉換成多電源供電系統，極大縮短配電網停電的時間，從而提高配電網的可靠性。具體數學模型為

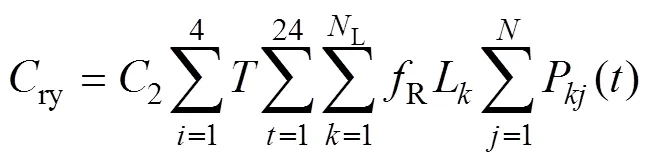
1.5 最低點電壓偏移量

DG并網不僅能夠提高配電網的可靠性，而且能夠改善配電網的電能質量。本文根據節點電壓偏移量的大小衡量電壓質量的優劣，具體如式（14）所示：

1.6 約束條件

本文在滿足等式及不等式約束的條件下，對DG和儲能裝置進行合理的優化配置。

1）節點潮流約束

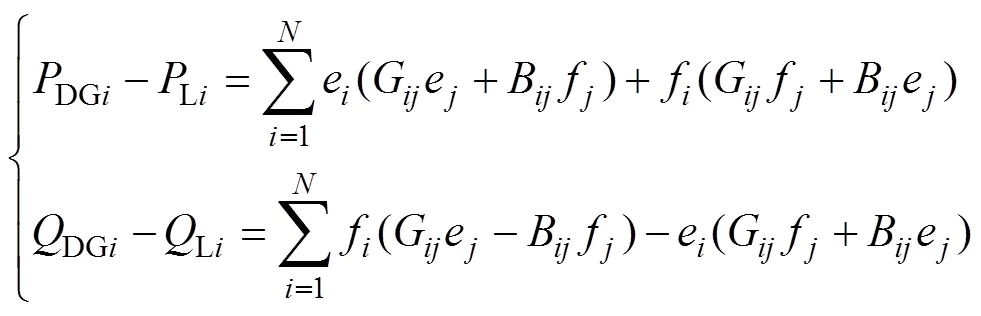
2）節點電壓約束

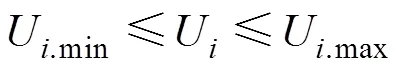
3）配電網接納DG的約束

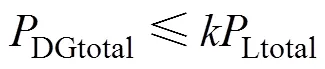
4）支路功率約束

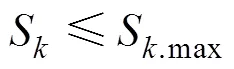
2 DG出力與負荷的時序特性

不考慮時序特性的規劃結果一般會產生偏差，如最大負荷與DG最大出力往往不在同一時段出現，因此獲得的DG容量配置結果缺乏合理性。考慮時序的全過程模擬，將使規劃結果更接近于實際，有利于真實反映配電網的各項經濟技術指標，以及實現風、光發電資源的互補。

2.1 光伏出力的時序性

光伏發電機組的輸出功率隨著光照強度的增強而增大，反之隨著光照強度的減弱而減小。4個季節中的典型日都在中午時刻輸出最大功率，但是在夜間光伏發電機組的輸出功率均為0。在4個季節中，夏季發出的功率最大而冬季發出的功率最小，具體如圖1所示。

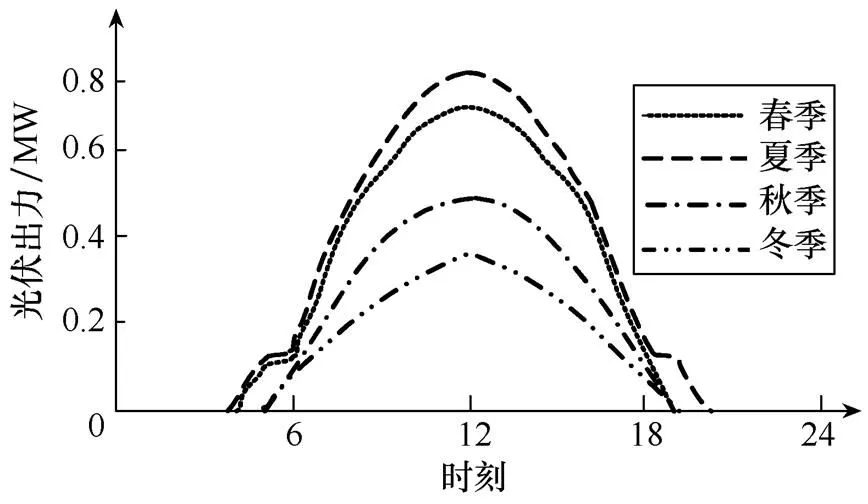
圖1 光伏出力

2.2 風電出力的時序性

風電輸出功率的規律性比光伏發電輸出的規律性差，不像光伏發電那樣4個季節的典型日都在同一個時刻達到最大值，風電在一天中出力的波動幅度較小。在4個季節中春秋季節發出的功率較大，夏冬季節發出的功率較小，具體如圖2所示。

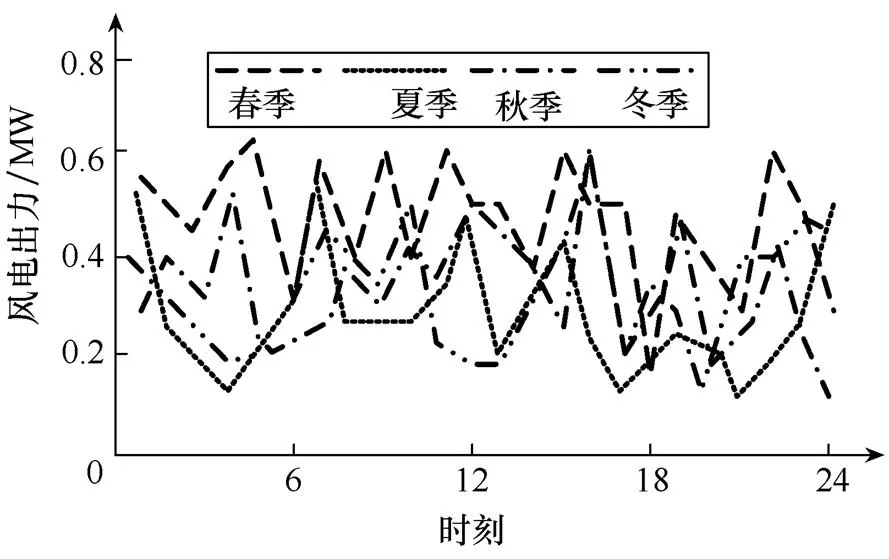
圖2 風電出力

2.3 負荷的時序性

本文將所研究的負荷分成4類，第一類為工業負荷，第二類為商業負荷，第三類為市政生活，第四類為農業負荷。由圖3可知，工業負荷在典型日的波動幅度較小而商業負荷的波動幅度較大，其用電高峰主要集中在15∶00—17∶00左右和7∶00—10∶00。市政生活負荷較小，其用電高峰主要集中在15∶00—20∶00。農業負荷一天的波動性最小。具體如圖3所示。

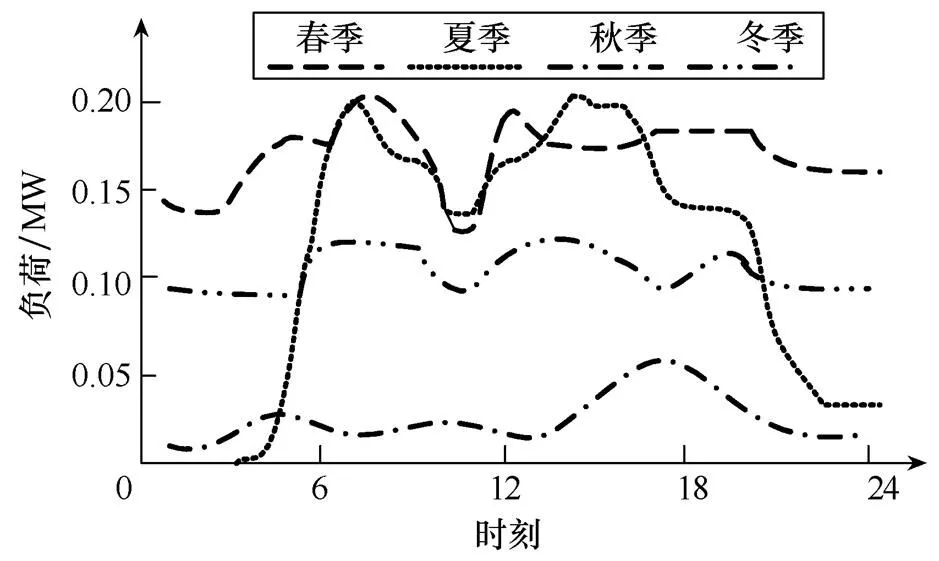
圖3 時序性負荷

3 基于時序性的儲能裝置充放電策略與算法求解

3.1 等效時序負荷

本文將一年分成365×24=8760個時間段，假設每個時間段內DG的出力和負荷保持不變，令時刻節點的負荷為，DG出力為，則節點在時刻的等效負荷為

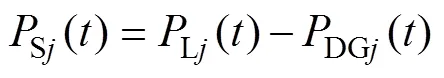
3.2 儲能裝置的充放電策略

受DG出力和負荷的時序性以及DG并網容量的限制，可能出現DG出力與并網功率不匹配的現象，為了充分平抑等效負荷的波動性，需要將多余的電能進行存儲并在缺電時進行補償。當DG出力大于負荷需求時，儲能裝置進行充電；當負荷需求大于DG出力時，儲能裝置進行放電。如果用蓄電池存儲（釋放）這部分電能，就會造成蓄電池頻繁充放電的現象，嚴重損害蓄電池的使用壽命，因此本文提出一種混合儲能的充放電策略。本文中的儲能裝置由超級電容和燃料電池兩部分構成，超級電容造價適中，可充放電次數多適用于小功率頻繁充放電的場合，而燃料電池存儲容量大不適合頻繁充放電。本文結合兩者的優點協調運行，當

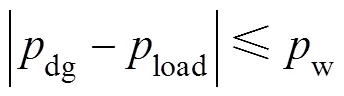
超級電容進行充放電；當

（21）

3.3 基于云模型的NSGA-II

模糊性和隨機性是不確定性的兩個方面，而不確定性是遺傳算法的基礎，但是在傳統的研究方面，通常不能很好地兼顧兩者，因此李德毅教授[10]提出云模型用一個統一的模型實現定性概念與定量描述之間的不確定轉換。云模型的數字特征用期望值，熵和超熵來表示，云發生器主要有正向云發生器、條件云發生器、條件云發生器等。

1）云初始化

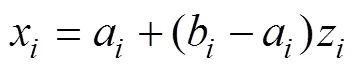
遺傳算法的初始化是影響最終解的關鍵步驟，因此初始化時個體的各個變量應盡可能分布廣，云初始化時產生的隨機數比混沌初始化產生的隨機數分布范圍廣而且穩定，因此云初始化產生的初始種群比混沌初始化產生的初始種群多樣性高可以有效避免局部收斂。

2）云交叉算子

針對傳統的NSGA-II交叉概率恒定缺乏靈活性的缺點，本文提出一種改進的自適應云交叉算子。在種群進化的過程中假設父代雙親的適應值分別為和（本文采用下文的權重將其轉化為單目標），父代種群中最大和最小適應值分別為、，則種群的交叉概率為

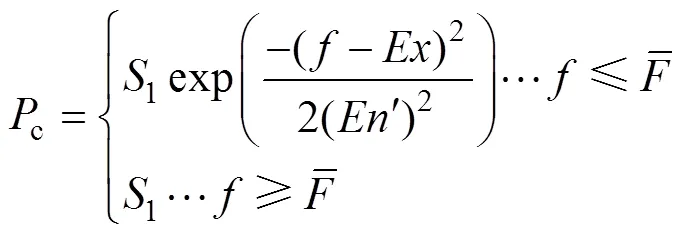
3）云變異算子

傳統遺傳算法變異概率恒定，如果設定的變異概率過大，則在進化后期會破壞適應值較好的個體，反之如果變異概率過小，則會使進化的過程緩慢。雖然國內外專家學者已經提出各種改進的方法，但仍然存在一定的缺陷，不符合生物進化的隨機性，因此本文引用基于云模型的云變異算子，具體的求解表達式為

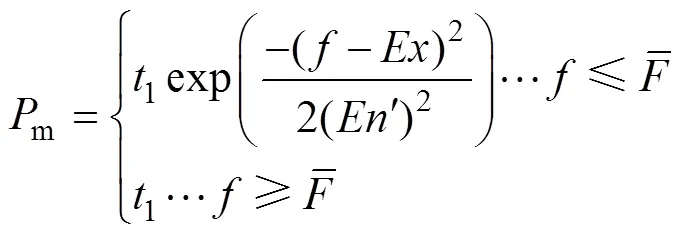
3.4 基于改進云模型NSGA-II算法求解

本文充分考慮DG，負荷以及儲能裝置在時序上的互補特性，將DG和儲能裝置的選址定容在時序上進行協同優化，建立多目標分布式電源優化配置的規劃模型，該模型采用改進的云模型NSGA-II進行求解。具體的求解步驟如下：

1）輸入風電、光伏在四季典型日的出力以及各節點的時序負荷。

2）設定種群的大小和迭代次數，并采用云初始化對種群進行初始化。

3）計算各節點在各時段的等效負荷以及儲能裝置在各時段的充放電功率，并采用前推回代法進行潮流計算。

4）根據上述的數學模型，求解各個個體的目標函數值。

5）根據各個個體的各個目標函數值進行非支配排序和局部搜索。

6）進行遺傳操作，并將產生的子代與父代合并。

7）對合并后的種群進行非支配排序和局部搜索，并選擇適應度較優的個個體。

8）進入下一代操作，直到達到迭代次數為止。

4 算例分析

由于對配電網一般采用閉環設計開環運行的供電方式，所以大多數配電網呈放射狀[4]。針對此特點，本文選用含33個節點，32條支路的10kV輻射狀網絡對上述模型和算法進行仿真測試，仿真結構圖如圖4所示。

圖4 IEEE-33節點系統結構圖

優化算法參數設置NSGA-II種群大小為50，總進化代數為100代NSGA-II，其他數據參考文獻[7-10]。

本文采用1—9標度法與隸屬度函數相結合的方法對尋優結果的pareto前沿解進行評價，具體1— 9標度法和隸屬度函數的求解方法見文獻[16]。

以下內容為方案設置及其尋優結果。

本文提出考慮時序、環境成本、儲能效益以及政府補貼的分布式電源和儲能裝置協同優化配置模型，并采用改進云模型NSGA-II對上述模型進行求解，為了證明所提方案的有效性同時對以下6種方案進行尋優：①采用基本的NSGA-II對上述模型進行求解；②分布式電源只考慮風電出力其他不變；③分布式電源只考慮光伏出力其他不變；④分式電源由風力發電和光伏發電配合其他不變；⑤除不考慮時序性外其他不變；⑥本文所提的模型和算法。具體DG和儲能設備的配置及費用見表1和表2。

本文通過1—9標度法求得各指標的權重分別為[0.1740, 0.2170, 0.1300, 0.3910, 0.0869]，年社會成本的最大值等于600，同理其他4個指標的最大值依次等于1200.00, 150.00, 120.05。文中所求的各個方案是指在該種情況下pareto解中指標值最小的方案。

②與⑥相比，雖然其年社會成本減少了58.5萬元，但是由于風電出力波動性較大，限制其并網的功率，因此其年購電成本、年環境成本以及年可靠性成本均高于⑥，同理各節點的電壓質量也低于⑥。③比②多裝一臺DG，因此其年社會成本高于②，但其購電成本和環境成本較低。由于光伏出力晝夜波動性極大，因此其可靠性成本高電壓質量差。④同時考慮了風電和光伏所以其年社會成本均比②和③高，但是由于風光在時序上具有互補性，在一定程度上可以提高其并網的能力，因此其購電成本，環境成本，可靠性成本均比較低，電能質量比較高，與⑥相比雖然其減少了投資成本但是它忽略了儲能裝置的效益，在時序上DG與儲能裝置配合可以大大提高DG的利用率。因此⑥的各項指標均優于④。⑤未考慮時序性，在任何時刻各節點的負荷均以最大負荷計算，所以其購電成本，環境成本，可靠性成本均比較高電能質量比較差，該方案與實際偏差較大沒有參考價值。①與⑥的pareto解如圖5、圖6所示。

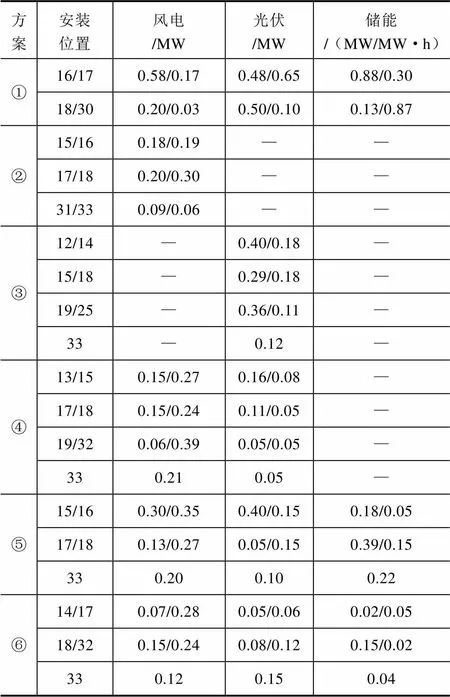
表1 DG安裝位置及容量

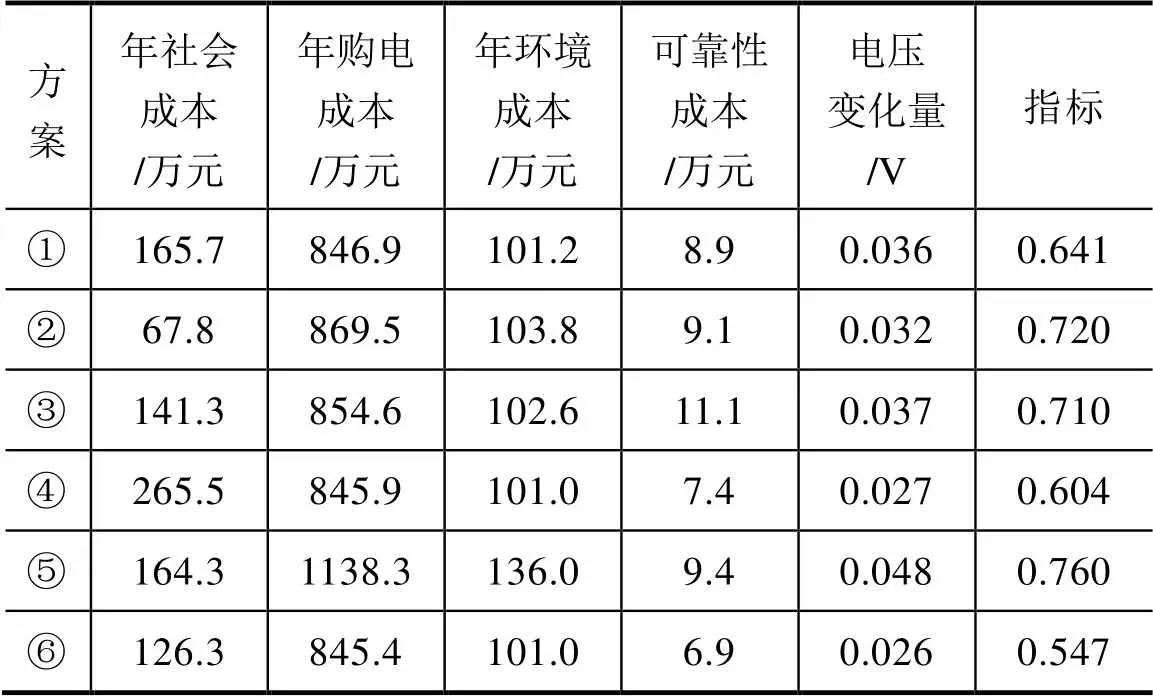
表2 尋優結果及評價

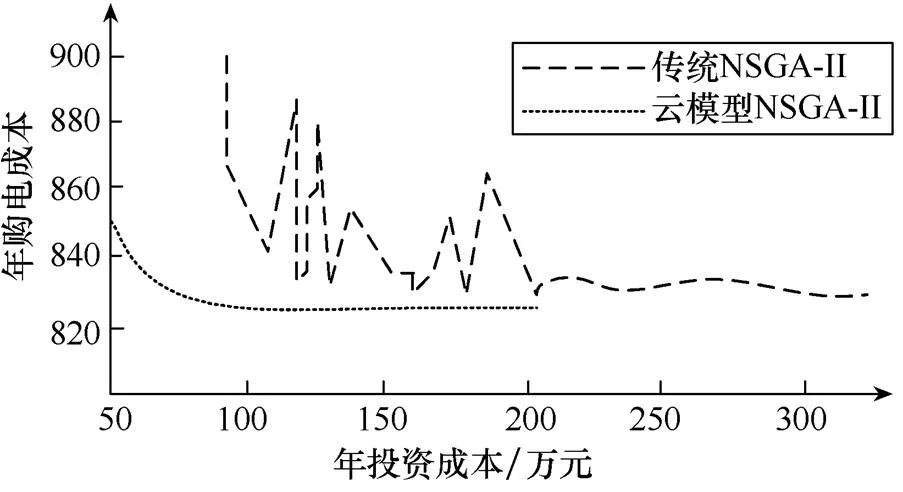
圖5 算法對比二維圖

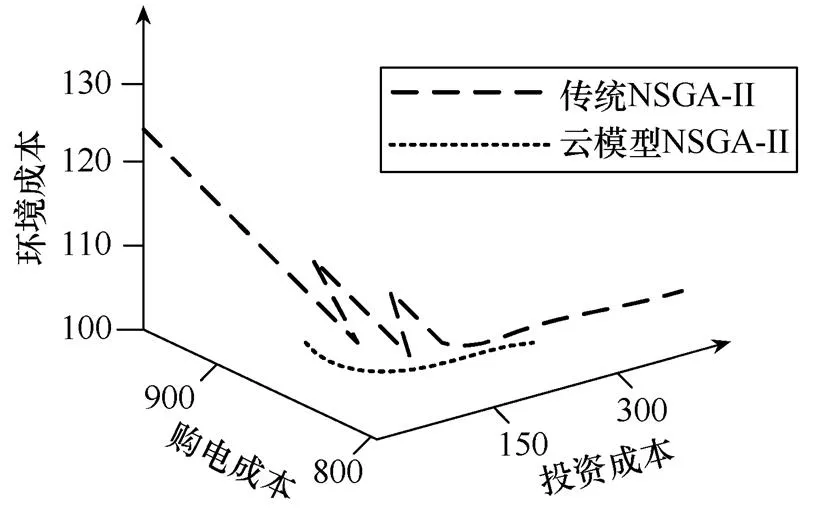
圖6 算法對比三維圖

由圖5和圖6可知改進的云模型NSGA-II比傳統的NSGA-II收斂的速度快，而且可以找到全局最優解，同時改進后的算法在最優解端面分布比傳統算法均勻。

5 結論

本文基于DG和負荷的時序特性，以降低系統年運行費用和提高電能質量為目標，對DG和儲能設備進行協同優化，建立分布式電源與儲能裝置優化配置的規劃模型，并采用基于云模型的NSGA-II進行求解得到最優配置方案。結果表明：①考慮DG和負荷的時序性更符合負荷和DG的實際運行情況，同時考慮時序性能充分發揮儲能設備的優勢；②儲能裝置、DG和負荷的協同優化可以有效控制等效負荷的波動，同時可以極大提高DG的滲透率；③改進的云模型NSGA-II比原始算法收斂速度快，而且能夠找到全局最優避免局部收斂。總之，本文所提的模型和算法可以對分布式電源和儲能裝置進行合理的優化配置，達到經濟性好電能質量高的目的。

[1] 夏澍, 周明, 李庚銀. 分布式電源選址定容的多目標優化算法[J]. 電網技術, 2011, 35(9): 115-121.

[2] 栗然, 馬慧卓, 祝晉堯, 等. 分布式電源接入配電網多目標優化規劃[J]. 電力自動化設備, 2014, 34(1): 6-13.

[3] 李亮, 唐巍, 白牧可, 等. 考慮時序特性的多目標分布式電源選址定容規劃[J]. 電力系統自動化, 2013, 37(3): 58-63, 128.

[4] 張節潭, 程浩忠, 姚良忠, 等. 分布式風電源選址定容規劃研究[J]. 中國電機工程學報, 2009, 29(16): 1-7.

[5] 李洪志, 楊俊友, 崔嘉. 考慮網損和電壓的多分布式電源最優選址和定容研究[J]. 電氣工程學報, 2015, 10(9): 79-86.

[6] 張沈習, 李珂, 程浩忠, 等. 間歇性分布式電源在主動配電網中的優化配置[J]. 電力自動化設備, 2015, 35(11): 45-51.

[7] 蘇海鋒, 胡夢錦, 梁志瑞. 基于時序特性含儲能裝置的布式電源規劃[J]. 電力自動化設備, 2016, 36(6): 56-70.

[8] Pesaran M, Abdullah A M Z, Khairuddin A, et al. Optimal sizing and siting of distributed generators by a weighted exhaustive search[J]. Electric Power Components and Systems, 2014, 4211.

[9] Guerra G, Juan A. Martinez-Velasco. Optimum allocation of distributed generation in multi-feeder systems using long term evaluation and assuming voltage-dependent loads[J]. Sustainable Energy, Grids and Networks, 2016, 5.

[10] 郭鳳鳴. 基于云模型遺傳算法的研究[D]. 南京: 南京理工大學, 2013.

[11] 鐘清, 余南華, 孫聞, 等. 主動配電網分布式電源規劃及經濟性分析[J]. 電力系統及其自動化學報, 2014, 26(11): 82-86.

[12] 張建華, 曾博, 張玉瑩, 等. 主動配電網規劃關鍵問題與研究展望[J]. 電工技術學報, 2014(2): 13-23.

[13] 沈鑫, 曹敏. 分布式發電接入主動配電網的全局優化與研究[J]. 電氣制造, 2015, 10(6): 67-70, 77.

[14] 張燕, 李瑞超. 分析分布式電源入網對配電網供電可靠性的影響[J]. 電子測試, 2016(9): 124, 123.

[15] 李文文. 配電網中分布式電源的優化配置研究[D]. 吉林: 東北電力大學, 2015.

[16] 張躍, 楊汾艷, 曾杰, 等. 主動配電網的分布式電源優化規劃方案研究[J]. 電力系統保護與控制, 2015, 8(15): 67-72.

Study on the Optimization of Distributed Generation Considering the Cooperation of Sequential Characteristic and Energy Storage Equipment

Chen Congwei1Jiang Xiubo2Liu Lijun2

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116)

Based on the typical sequential characteristic of different types of load and distributed generation (DG), considering the environmental cost of different types of pollutants and Energy storage efficiency,a multi-objective optimal allocation model of DG and energy storage equipment is established, which is applied to obtain the minimum annual social cost, annual electricity purchasing cost, annual environmental cost, annual reliability cost and voltage deviation. The model executes collaborative optimization of the location and capacity of DG and energy storage equipment based on the sequential characteristic of load and DG output. Meanwhile, to solve the problems that the NSGA-II algorithm has low initialization diversity, the probability of crossover mutation is constant and the convergence rate is low, the theory of cloud model is integrated into NSGA-II and the improved model is applied to optimize the model, the 1-9 scales method and membership function are combined to evaluate the results of optimization. Last, the model is simulated in IEEE-33 node system, the simulation results show that the model and algorithm can effectively optimize the site and capacity of DG and energy storage equipment.

energystorage equipment; cloud model; NSGA-II algorithm; sequential characteristic; distributed generation

福建省中青年教師教育科研基金資助項目（JA14064）