基于S7-300 PLC 的單神經元 PID 控制器設計與實現

陳 軍 李玉榕

?

基于S7-300 PLC 的單神經元 PID 控制器設計與實現

陳 軍 李玉榕

（福州大學電氣工程與自動化學院，福州 350116）

PID控制器在被控對象具有非線性特性或運行環境發生變化時，PID的固定參數導致控制系統性能下降。針對該問題，本文提出在S7-300 PLC上設計和實現基于Hebb學習規則單神經元PID控制器。首先根據神經元的學習能力，設計了基于Hebb學習規則的單神經元PID控制器，仿真測試表明相對于PID控制器，基于Hebb學習規則的單神經元PID能夠自適應調整控制器參數，具有系統響應速度快和超調量小等優點。最后在S7-300 PLC上實現了基于Hebb學習規則的單神經元PID控制算法，對溫度對象進行控制。實驗結果表明，基于Hebb學習規則的單神經元PID算法簡單，在PLC上易于實現，有效改善系統性能。

單神經元PID；自適應控制；S7-300 PLC；Hebb學習規則

在工業控制中，PID控制由于其算法簡單、易于實現、可靠性高，得到廣泛應用，并且也將在很長一段時間內作為主要控制方法存在著。PID控制器的參數是根據被控對象的數學模型整定的，當被控對象的參數具有時變性、不確定性、非線性或運行環境發生變化時，PID控制器的參數無法自適應調整，造成控制效果下降[1]。為解決這個問題，基于神經網絡的PID控制器一類智能控制算法，即利用神經網絡的學習能力和自適應能力實現PID控制器參數自適應調整得到了廣泛研究：基于各種復雜改進學習規則的單神經元PID控制器[2-4]，基于二次型性能指標的單神經元PID控制器[5]，基于BP神經網絡、RBF神經網絡、Hopfield神經網絡的PID控制器等[6-9]。這些復雜控制器雖然可以取得較好的控制性能，但這些控制器的算法運算量較大，因而目前基于神經網絡的PID控制器的研究多局限于仿真研究[10-12]。而在實際工業應用中，在控制器中算法實現所需的運算量是保證系統能夠實時運行的關鍵問題。

實際工業應用環境受到各種通常高粉塵、高噪聲、強電磁干擾和溫度變化的影響，可編程序控制器（programmable logic controller，PLC）是工業環境下的典型控制裝置。為提高控制系統性能以解決傳統PID算法控制不能克服的問題，在PLC上實現智能控制算法并應用至實際生產過程中是十分有意義的。

在基于神經網絡的PID控制器中，基于Hebb學習規則的單神經元PID控制器結合了人工神經元和PID控制器二者的優點，具有較好的適應能力且算法簡單，易于實現。因此，本文首先通過仿真驗證了基于Hebb學習規則的單神經元PID控制算法在解決滯后對象控制問題的可行性，然后在西門子S7-300 PLC上實現了單神經元PID溫度控制系統，取得較好控制效果。

1 單神經元PID控制算法

1.1 離散PID控制器

當控制器采用數字計算機實現時，各種數據的處理在時間上是離散的。離散PID控制算法就是由模擬PID控制算法經過數字化得到的。通常數字PID有位置式和增量式兩種形式。由于增量式PID只輸出增量，避免輸出大幅變化，誤動作時營銷較小，故本文選取的PID結構為增量式PID。增量式PID控制算的輸出表達式，如式（1）和式（2）所示：

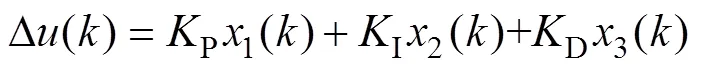
（2）

式中，1、2、3為離散PID控制算法的比例、積分、微分三部分輸入，P、I、D為PID的參數。傳統PID控制器的參數是工程整定法，基于被控對象具體數學模型的ZieglerNichols經驗公式法等。這些方法都是根據被控對象處于某一個確定的工作狀態整定的，參數固定不具有自適應能力。

1.2 基于Hebb學習規則的單神經元PID控制器

人工神經元是對神經元細胞基本功能和特性的抽象，是一種線性組合器和具有激活函數的多輸入單輸出單元。模擬生物神經元由于不同的突觸對脈沖輸出過程影響，人工神經元利用加權系數正負模擬神經元突觸的興奮或抑制，其大小則代表連接強度的大小[13-14]。人工神經元的模型，如圖1所示。

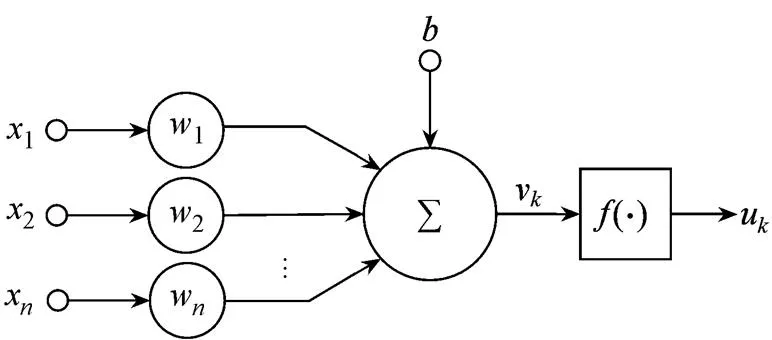
圖1 人工神經元模型

根據上述模型，人工神經元的輸出表達式為

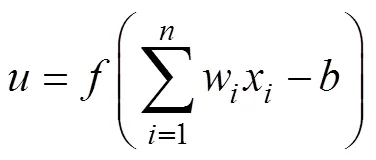
式中，x為神經元的輸入；w為權重系數；為閾值；(·)為激活函數。可以根據一定的學習算法，學習和調整權重系數。

根據上文的人工神經元模型，將傳統PID輸入作為人工神經元的輸入，神經元的權重系數作為PID控制器的P、I、D參數，構成單神經元PID控制算法的基本結構[13]。通過學習規則在線調整神經元不同輸入的連接強度，由神經元通過關聯搜索產生下一時刻的控制量。單神經元自適應PID閉環系統的控制結構框圖，如圖2所示。

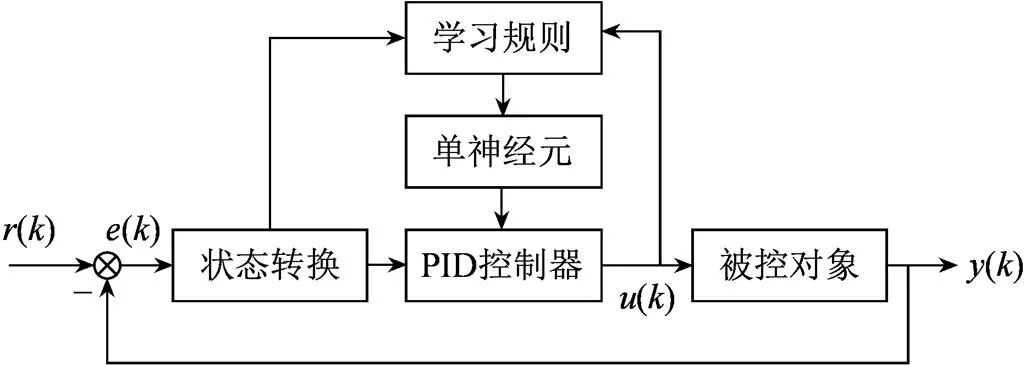
圖2 單神經元PID系統框圖

選取有監督的Hebb學習規則[15]，則單神經元控制器的數學表達式為

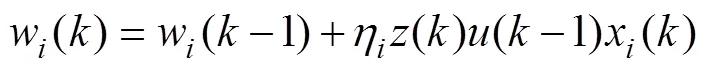
（5）

式中，（=1，2，3）為單神經元PID控制器的比例、積分、微分3個分量的學習速率，各學習速率系數獨立，可以實現分別調整；w（=1，2，3）為權值系數；()為教師信號，本文中學習規則中是以誤差信號()作為教師信號。

根據人工神經元模型的輸出表達式，取閾值為0，激活函數為線性傳遞函數，則該神經元的輸出為

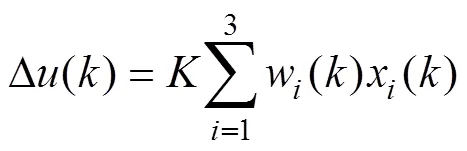
式中，為增益系數；w為輸入x的作用強度系數，其作用與傳統PID控制器的參數P、I、D類似。但與傳統PID算法的參數不可調所不同的是，單神經元PID的權值是具有在線調整能力的[1]。在被控對象數學模型發生變化，或者運行環境發生變換時，神經元的權重系數能夠根據學習算法進行適應。

2 仿真測試

2.1 仿真條件

仿真測試選取的數學模型為加熱器的典型數學模型。根據文獻[16]的建模結果，對象的數學模型為

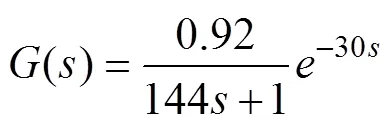
選取的對象數學模型的時間常數和純滯后都較大，控制器不能及時產生控制，影響控制質量。

仿真是基于Matlab的Simulink工具箱中的S函數實現。S函數模塊包括S函數模型塊和S函數源文件兩部分。本文以M文件為源文件編寫S函數。仿真的系統框圖中，加入了非線性飽和環節用于限制控制器輸出的控制量，防止輸出過大。仿真系統的結構框圖如圖3所示。

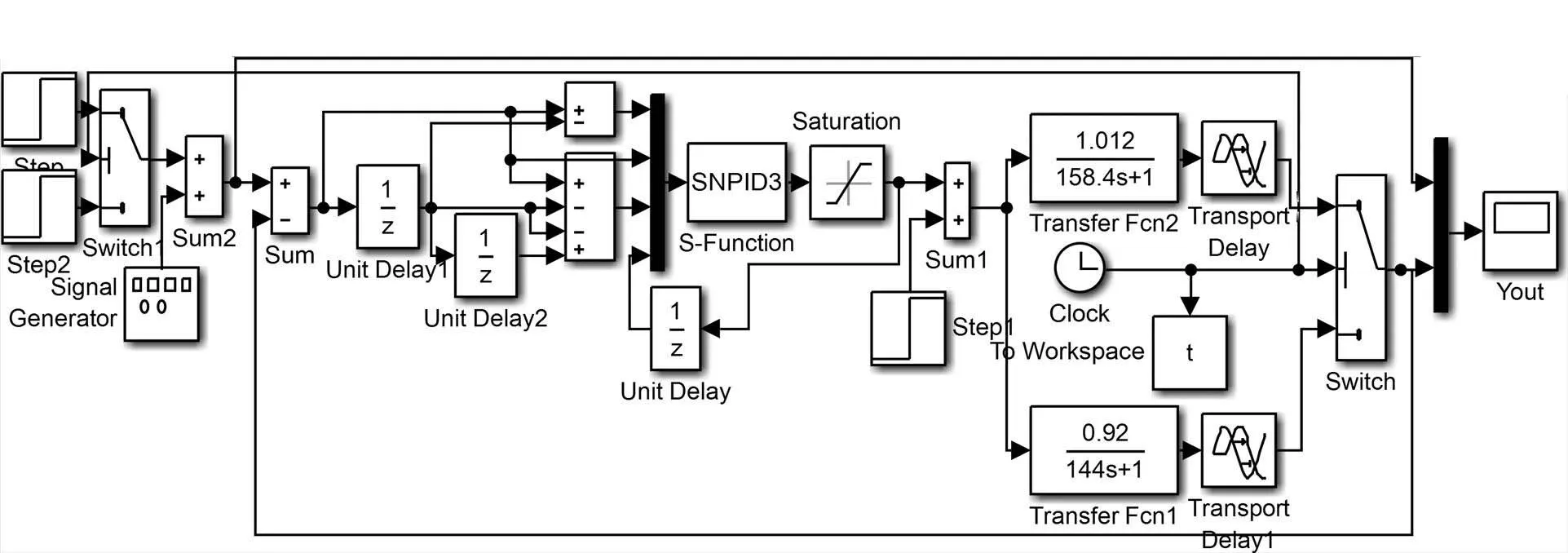
圖3 單神經元PID在Simulink中的仿真模型

2.2 仿真結果

1）仿真實驗首先利用Z-N公式計算并試湊一組PID控制器的參數。根據式（7）被控對象數學模型，確定P=6.14，I=0.0167，D=15。將這組PID參數作為單神經元PID控制器的3個權值的初值。這樣做既節省了參數獲取的時間，也避免了更多的主觀因素，同時也使兩種控制器更具有可比性。選取的單神經元PID的學習速率為1=6，2=0.01，3=1，增益=5。在=1500s時，加入擾動，測試擾動下的控制效果。實驗對比結果，如圖4所示。

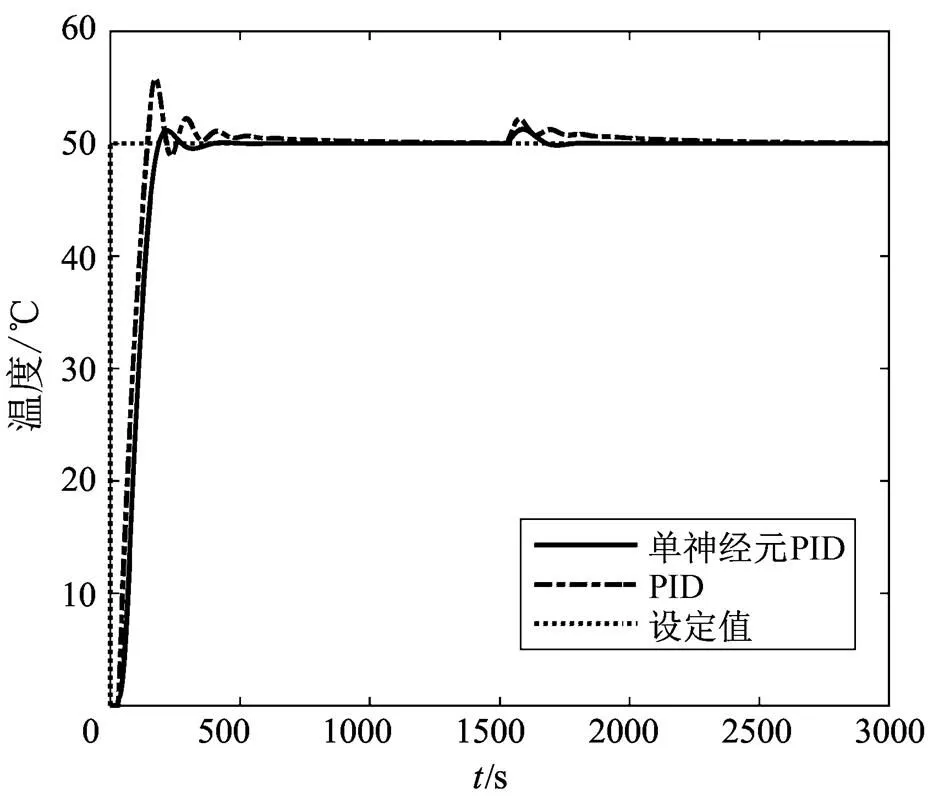
圖4 PID與單神經元PID的階躍響應

2）在上組實驗的基礎上測試系統工作點發生變化導致模型變化時，PID和神經元PID控制器的控制效果。設計被控對象數學模型的時間常數和增益系數的變化均為增加20%，則在=2000s時，模型變化為

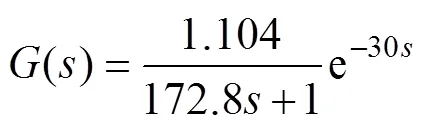
以此模擬對象在不同工作點的不同模型特性。工作點變化導致模型變化下的響應曲線如圖5所示。PID和神經元PID的性能指標對比，見表1。

表1 PID和單神經元PID階躍輸入和擾動下的性能對比

從表1可知，從仿真結果可以得出相比于傳統PID控制，階躍輸入情況下，單神經元PID控制的超調量小，調節時間短，控制性能更好。對于外部擾動，對比于PID，單神經元PID對于擾動的響應比較快，很快恢復了設定值且波動較小。對于模型變化的測試，單神經元PID的超調量和調節時間均遠小于PID控制器。綜上所述，仿真內容驗證了單神經元PID控制器的有效性，單神經元PID易于實現，且控制效果優于PID。

3 基于S7-300 PLC的控制器實現

3.1 閉環系統結構

為驗證基于Hebb學習規則的單神經元PID控制算法在PLC上的可實現性與實際應用效果，設計的基于S7-300 PLC的溫度閉環控制系統如圖6所示。

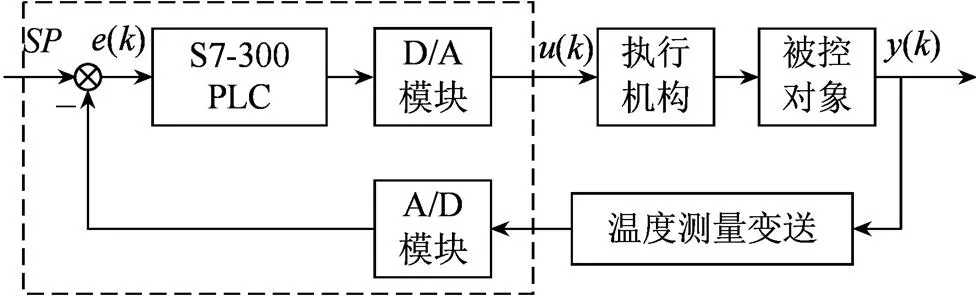
圖6 實際溫度控制閉環系統框圖

圖6中，實際系統的硬件選型：

1）控制器。選用的PLC為西門子公司的S7-300系列的CPU 312，該CPU具有0.2ms/1000條指令執行速度，32KB工作存儲器，滿足控制需求。在PLC上分別實現PID控制算法和單神經元PID控制算法，用于對比控制效果。

2）被控對象。電加熱器。

3）執行機構。脈寬調制方式，輸入可選擇模擬量輸入或開關量輸入，輸入范圍為0～10V。

4）溫度測量變送。溫度傳感器采用PT100熱電阻。溫度變送輸出可選擇0～5V量程和0～10V量程輸出。

5）D/A和A/D模塊。溫度傳感器輸入和控制量輸出均為模擬量，故選擇DA模塊模擬量輸入模塊SM331。

3.2 實現

為驗證單神經元PID控制器在PLC上實現的可行性和控制器的控制效果，設計對比實驗。在西門子S7-300 PLC上分別編寫普通PID和單神經元PID控制程序，對電加熱器的溫度進行控制，對比控制效果。

首先，PID控制器采用S7-300固件中內置的PID功能塊FB41實現。單神經元PID程序采用梯形圖語言（LAD）編寫。編程環境為西門子公司的全集成自動化軟件博途V13（TIA portal）。程序塊和數據塊的關系規劃圖，如圖7所示，說明了單神經元PID實現的LAD程序所涉及的功能塊、數據塊的 關系。

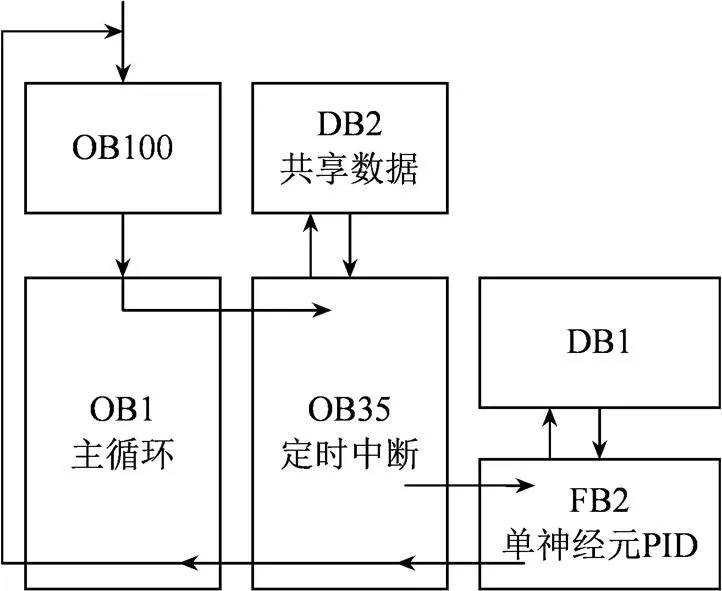
圖7 程序塊規劃圖

利用功能塊，將單神經元PID控制算法封裝為功能塊FB2。FB2的輸入接口包括設定值、過程值、增益系數和學習速率，輸出接口為輸出。數據塊DB1作為FB2的背景數據塊，用于存放單神經元PID控制器的參數。DB2為全局數據塊，存儲全局變量和一些過程值。

具體的程序流程圖如圖8所示。在OB100初始化中，配置CPU定時中斷，循環定時中斷時間為500ms。OB35為定時中斷執行的程序塊。在該程序塊中執行的主要任務有：模擬量轉換、權值計算、輸出量計算、限幅判斷、數字量轉模擬輸出和數據更新。

3.3 實驗結果

實驗首先對PID進行參數整定，確定PID控制參數為P=2.0，I=0.1，D=0.2。與上文仿真相同，設置單神經元PID的權重系數初始值為普通PID參數值。單神經元PID控制器的其他參數選取為= 1.2，1=2.0，2=0.1，3=0.3。實驗的階躍輸入的設定值為50℃，在系統穩定后，即在=1100s時，加入外部擾動。基于S7-300 PLC實現的單神經元PID和PID控制器，在階躍輸入和擾動情況下的響應，分別如圖9和圖10所示。

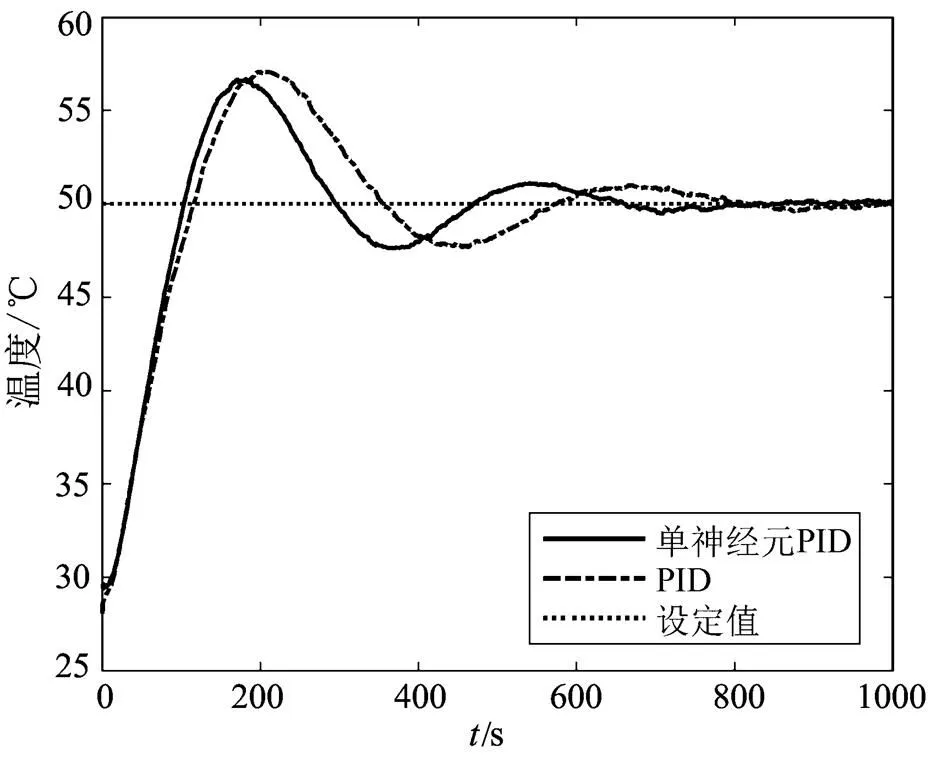
圖9 PID和單神經元PID的階躍響應的實驗測試

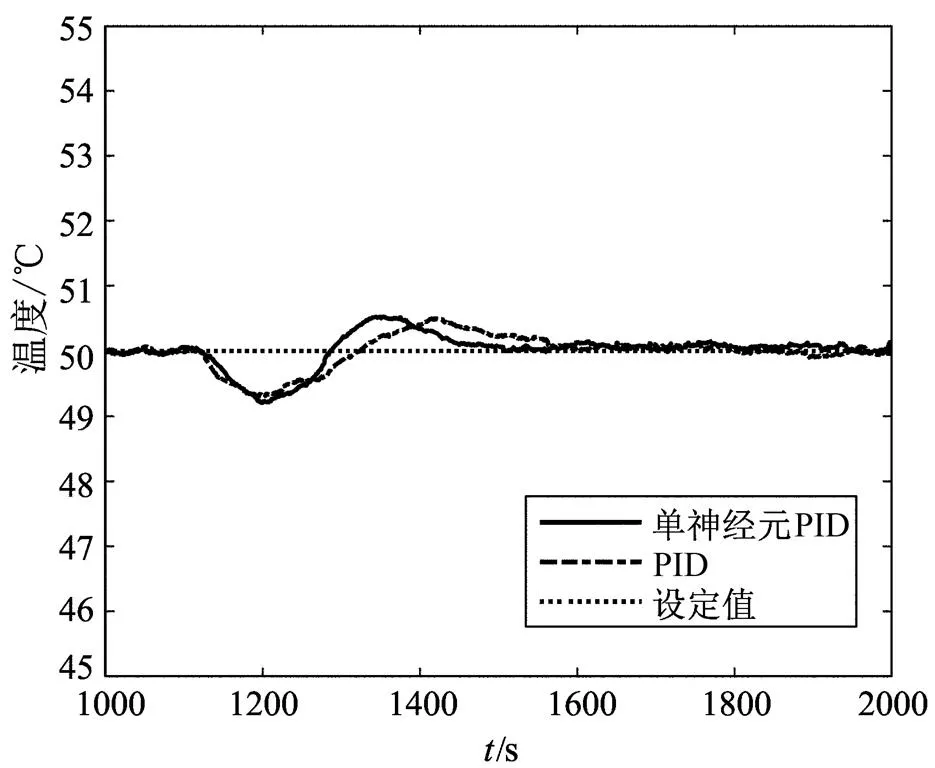
圖10 PID和單神經元PID的擾動響應

對比兩組控制器的響應曲線，可以發現單神經元PID的超調量、上升時間、調節時間等性能都優于普通PID控制器。擾動輸入的情況下，恢復速度較快。在S7-300 PLC平臺上實現單神經元PID控制器是可行的，且改善了控制效果。另一方面，實驗結果中單神經元PID比PID的控制性能提高效果不如仿真結果中的那么顯著，出現這種現象的原因可以從以下幾個方面考慮。首先，實際系統數據采集反饋并非如同仿真中的理想線性單位環節，這部分的非線性特性在仿真模型中沒有考慮。其次，實際PLC是循環掃描工作過程，以及采樣周期不同，與仿真運行的原理不同，也會對結果產生影響。并且，仿真時使用的是參考文獻[16]中提出的一種帶純滯后的二階系統數學模型，而實際實驗對象的數學模型可能與仿真的對象模型并不一致。本文實際實驗對象是實驗使用的小型電加熱箱，純滯后和慣性系數均較小，這使得實驗結果中單神經元PID相對于PID的優越性沒那么明顯。最重要的是，實驗部分使用PID模塊的是西門子S7-300 PLC中內置封裝的PID功能塊，該模塊的PID控制器是經過優化的，其本身控制性能已經較為理想，而仿真中使用的是基本的PID控制器，所以會出現仿真結果中單神經元PID比PID的性能好很多而實驗中兩者差距較小的情況。

4 結論

本文主要研究基于Hebb學習規則的單神經元PID控制器的設計、仿真和PLC實現。通過在Matlab中的仿真驗證了基于Hebb學習規則的單神經元PID控制器的控制效果。在此基礎上，在西門子S7-300 PLC上實現了基于Hebb學習規則的單神經元PID算法，利用實際電加熱器上進行實驗，與PID控制器進行對比，驗證了基于Hebb學習規則的單神經元PID控制器的可行性以及對系統性能的改善。

單神經元PID結合了PID控制器結構簡單、易于實現和神經元自適應能力的特點，使其可在現場工業控制器中實現，并且對于提高實際生產過程中具有非線性、時變性或不確定特性的對象的性能具有重要的意義。

[1] Chen B, Yang H, Wang L. Single neuron PID control of aircraft deicing fluids rapid heating system[J]. Journal of Networks, 2013, 8(2): 405-412.

[2] Wang X J, Hu X H. An improved control strategy of single neuron PID[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(8): 1498-1501.

[3] 張麗麗, 王玉惠, 陳哨東, 等. 基于改進的神經元 PID 戰術網絡擁塞控制[J]. 電光與控制, 2013(10): 14-17.

[4] 岳舟. 基于神經元PID控制的Buck-Boost矩陣變換器研究[J]. 高技術通訊, 2015, 25(12): 1069-1075.

[5] Kusumoputro B, Rif'an M. Performance characteristics of an improved single neuron PID controller using additional error of an inversed control signal[C]//2015 World Congress on Industrial Control Systems Security (WCICSS), 2015: 58-62.

[6] 王同旭, 馬鴻雁, 聶沐晗. 電梯用永磁同步電機BP神經網絡PID調速控制方法的研究[J]. 電工技術學報, 2015(S1): 43-47.

[7] 李勇. 基于優化PID的食品加工恒溫控制研究[J]. 電氣技術, 2015, 16(12): 76-80.

[8] Chen Yifei, Xu Sen, Cao Rui, et al. The study and simulation of PID control based on RBF neural network[C]//International Conference on Electronic and MechanicalEngineering and Information Technology. Heilongjiang, China, 2011: 3453-3456.

[9] Wei D, Feng X. Research and simulation of PID model reference adaptive control based on hopfield network[J]. Modern Electronics Technique, 2009, 11.

[10] 高利軍. 一種用于大型機組設備智能控制方法的研究[J]. 控制工程, 2016, 23(4): 490-493.

[11] 徐國華, 李祖佳, 賀磊, 等. 單神經元PID在絞車控制系統中的應用[J]. 控制工程, 2013, 20(1): 42-45.

[12] 孫亮, 孫啟兵. 神經元PID控制器在兩輪機器人控制中的應用[J]. 控制工程, 2011, 18(1): 113-115.

[13] Fang H, Yu X. Design and simulation of neuron PID Controller[C]//Information Technology, Computer Engineering and Management Sciences (ICM), 2011 International Conference on. IEEE, 2011, 1: 80-82.

[14] 竇真蘭, 施剛, 曹云峰, 等. 減少風力機轉矩波動的異步變槳控制[J]. 電工技術學報, 2014, 29(1): 236- 245.

[15] Liu C Y, Wang M H, Li D W. Combined control of Single Neuron PID and normal PID of switched reluctance motor[C]//International Conference on Consumer Electronics, Communications and Networks. IEEE, 2011: 146-149.

[16] 許玉忠. 基于自適應模糊PID控制的電阻爐溫度控制系統[J]. 華北水利水電學院學報, 2011, 32(2): 83- 86.

Designand Implementation of Single Neural PID on S7-300 PLC

Chen Jun Li Yurong

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116)

When controlled object is nonlinear or operating environment changes, the fixed parameters of PID will cause performance degradation. To solve this problem, a single neural PID based on Hebb learning rule is designed and implemented on S7-300 PLC in this paper. Firstly, a single neural PID based on Hebb learning rule according to the adaptive feature and learning ability of neuron. The simulation shows that, with respect to PID, single neural PID based on Hebb learning rule can adaptively adjust, thereby the system is of faster response, small overshoot. Then, single neural PID is implemented on S7-300 PLC to control the temperature of heater. The experiment show that single neural PID based on Hebb learning rule is simple and practical on PLC and can significantly improve system performance.

single neuron PID; adaptive; PLC; Hebb learningrule

陳 軍（1993-），男，福建莆田人，碩士研究生，主要研究方向為工業控制系統與應用。

國家自然科學基金（61403319）

福建省教育廳科技項目（JK2014001）

福建省科技廳國際合作項目（2015I0003）