有缺失數據的加權指數總體參數估計的漸近性
李開燦,張文強
(湖北師范大學 數學與統計學院,湖北 黃石 435002)
有缺失數據的加權指數總體參數估計的漸近性
李開燦,張文強
(湖北師范大學 數學與統計學院,湖北 黃石 435002)
依照隨機變量變換可以重新參數化的思想,得到了一種加權指數分布總體在具有缺失數據情況下參數的極大似然估計,利用中心極限定理和相關的極限理論,證明了這種估計量的強相合性和漸近正態性。
加權指數分布;缺失數據;極大似然估計;漸近正態性
0 引言
指數分布是可靠性分析中重要的分布,因為許多電子元器件的壽命可以用它來刻劃。近年來由于對系統可靠性研究的深入,人們覺得以前的單參數或雙參數指數分布還有進一步發展的需求,例如在并聯系統的可靠性研究中,若并聯系統元件有不同的壽命分布,那么系統的可靠性分布就不是單參數或雙參數指數分布,文獻[1]、[2]提出了兩類加權指數分布,其實文獻[1]、[2]的分布形式還可以進一步拓展,由于它不是本文研究的主題,我們暫且回避不談。但是加權指數分布所具有的性質,特別是和指數分布類似的性質是需要研究的。
在雙參數或單參數指數分布研究中,近期有許多文獻研究了帶有缺失數據類型的參數估計的統計性質。文獻[3]研究了單參數且有缺失數據情行下參數估計的漸近性,文獻[4]對具有部分缺失數據雙參數指數總體的參數估計性質進行了討論,文獻[5]對單參數兩指數總體帶有缺失數據的參數估計問題進行了討論,給出總體參數估計的漸近性質、參數相等的檢驗以及參數差的漸近置信區間。
本文的主要目的是研究文獻[2]提出的加權指數分布在缺失數據下參數估計的漸近性問題。我們通過借助隨機變量轉化,得到一個新的包含原有參數的加權指數分布密度函數的機理,對密度函數中的未知參數重新參數化,進而得到了這個加權指數分布參數的極大似然估計,利用前面文獻類似的方法及其大數定律和中心極限定理,本文證明了加權指數總體下參數極大似然估計具有的強相合性和漸近正態性。
1 加權指數分布概述
在概率論中,人們通過直接定義密度函數來描述許多常用的分布,文獻[2]也這樣給出加權指數分布。若隨機變量Z有密度函數

(1)
其中I(z>0)是示性函數,α>1,λ>0是常數,則稱Z服從參數為α,λ的加權指數分布,記作Z~WE(α,λ)。
加權指數分布的產生機理文獻[2]從并聯系統做了一個全面的解釋,現在從隨機變量變換的方式給出產生原理。用X~Be(a,b)表示隨機變量X服從Beta分布,其密度函數為

若隨機變量U~Be(a,b),?c>0,令U=e-2cV,用確定隨機變量函數分布的常規方江(文獻[6]不難導出新隨機變量V的密度函數為

(2)
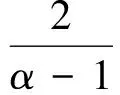
即得到加權指數分布的密度函數。這說明加權可靠指數分布可利用變量轉化由Beta分布生成。
注記1 通常α稱為形狀參數,λ稱為尺度參數.單獨從分布密度(1)式可以認為α、λ是獨立的,但是從產生機理不難發現,可以讓它們有某種關聯,這就是我們后面把這兩個參數關聯化的基礎。
2 問題的假設與參數極大似然估計
在文獻[1]、[2]都討論了加權指數分布參數的極大似然估計,[2]還給出了極大似然估計的極限性質,本節給出(1)式下有缺失數據的參數估計。需要指出的是本文討論的數據缺失機制都是完全隨機缺失的,即MCAR,細節見文獻[7].
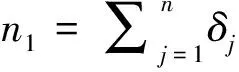

f(x,λ)=2λ(2λ+1)e-2λx(1-e-x)x>0
本文主要研究這類分布的極大似然估計及其漸近性質。
為了獲得缺失數據下λ的極大似然估計,首先確定其觀測到的數據X1,X2,…,Xn1的似然函數
從而對數似然函數為
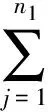
對數似然方程
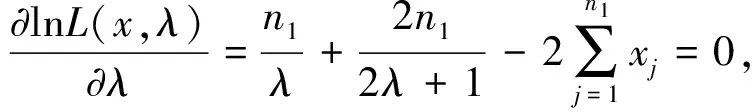
進一步可得方程的解
化簡即可得λ的極大似然估計為
3 未知參數極大似然估計的漸近性質
在本節主要討論上述有缺失數據的加權指數分布極大似然估計的漸近性質,為此先引入幾個引理。

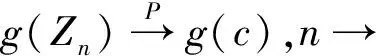
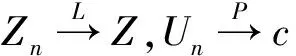
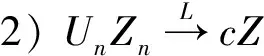
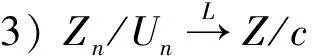
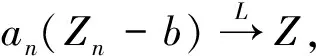

這幾個引理的證明都可以在文獻[8]中找到。
定理 在加權指數分布中,若參數和觀察樣本滿足本文§2的條件,那么當n→∞時,(3)確定的極大似然估計有如下漸近性質,
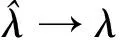
證明 由強大數定律可知當n→∞時,


令函數
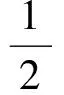
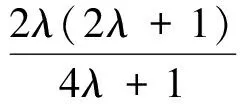
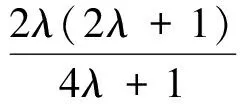
又由于
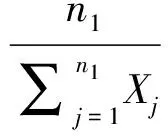
于是由引理1可得
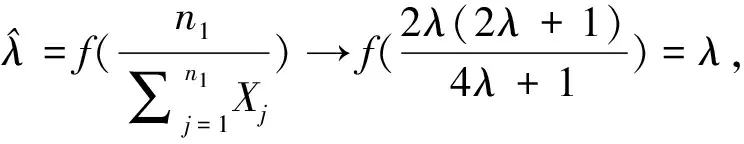
另一方面取函數
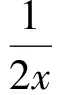
則

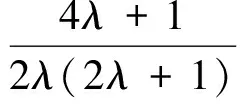
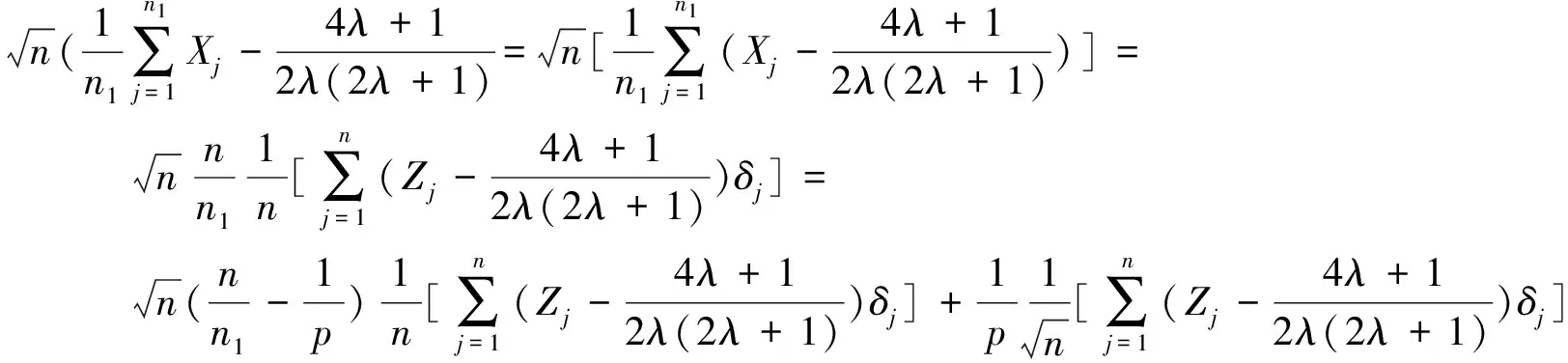
對于(4)式中的I2,由于
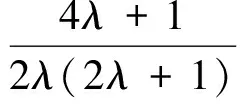
根據中心極限定理(見文獻[6])
于是有
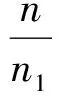
有
又由于
由引理3可知
證畢。
本文僅對加權指數分布在缺失數據情況下,利用所觀測到的數據對總體參數進行極大似然估計,不過也只是運用特殊參數化才做出的極大似然估計并證明了它的強相合性和漸近正態性,類似文獻[5],我們也可以對參數化的兩個加權指數總體帶有缺失數據的參數是否相等進行檢驗以及作出參數差的漸近置信區間在此不一一討論。另外,對加權指數分布若不進行特殊參數化,兩個參數有缺失數據如何研究估計的漸近性質還有待進一步的研究。
[1]Rameshwar D Gupta, Debasis Kundu. A new class of weighted exponential distributions[J]. Statistics-A Journal of Theoretical and Applied Statistics, 2009,43(6):621~634.
[2]劉大飛,李開燦.一類加權可靠指數分布[J].數學雜志,2013,33(4):689~696.
[3]劉銀萍.具有部分缺失數據兩個指數總體的估計和檢驗[J].吉林大學學報(理學版).2002.40(3):255~257.
[4]馬明月,宋立新.具有部分缺失數據兩個雙參數指數總體的估計[J].吉林師范大學學報(自然科學版),2004,(2):14~18.
[5]蘇 曦,郭鵬江,夏志明.兩指數總體帶缺失數據的參數估計與檢驗[J].三峽大學學報(自然科學版),2011,33(4):101~103.
[6]李開燦,蔡擇林.概率論[M].武漢:湖北科學技術出版社,2009.
[7]Little R J A, Rubin D B. Statistical Analysis with Missing Date[M].2nd edition. New York: Wily,2002.
[8]茆詩松,王靜龍,濮曉龍.高等數理統計(第二版)[M].北京:高等教育出版社,2006.
Abstract: By the ideal to transform expression of the random variable that one can do reparametrization for the old parameter in distribution, This paper gets the maximum likelihood estimation for the weighted exponential distributions with missing data. Further, using the limiting theory relating to the central limit theorem, the strong consistency and asymptotic normality of the estimation are also proved.
Keywords: the weighted exponential distribution; missing data; MLE; asymptotic normality
Theasymptoticalpropertyontheestimationofweightedexponentialdistributionwithmissingdata
LI Kai-can, ZHANG Wen-qiang
(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China)
O212.2
A
2096-3149(2017)03- 0001-05
10.3969/j.issn.2096-3149.2017.03.001
2017—06—02
國家自然科學基金資助項目(11471105)
李開燦(1962— ),男,湖北武漢人,教授,研究方向為多元統計分析.

