利用結(jié)構(gòu)導(dǎo)向平滑方法解釋斷層
問 雪 陳雪芳 陳勝紅 孟大江 唐明銘 吳 成
(中海石油(中國(guó))有限公司深圳分公司,廣東深圳518054)
利用結(jié)構(gòu)導(dǎo)向平滑方法解釋斷層
問 雪*陳雪芳 陳勝紅 孟大江 唐明銘 吳 成
(中海石油(中國(guó))有限公司深圳分公司,廣東深圳518054)
在深層地震資料解釋過程中,受資料品質(zhì)的限制,斷層解釋難度較大。為此,研究了對(duì)疊后地震資料進(jìn)行處理的基于梯度結(jié)構(gòu)張量的結(jié)構(gòu)導(dǎo)向平滑方法,該方法能有效改善地震資料的品質(zhì),進(jìn)而輔助斷層解釋。具體流程為:①利用原始地震數(shù)據(jù)求取每個(gè)采樣點(diǎn)在空間(或時(shí)間)方向的導(dǎo)數(shù),并求取梯度結(jié)構(gòu)張量矩陣;②通過特征分解求取梯度結(jié)構(gòu)張量矩陣的特征向量,并構(gòu)建擴(kuò)散張量矩陣;③將擴(kuò)散張量矩陣代入改進(jìn)的偏微分?jǐn)U散方程,采用共軛梯度迭代法求解該方程,求得的解即為平滑后的圖像。實(shí)際資料處理結(jié)果表明:經(jīng)結(jié)構(gòu)導(dǎo)向平滑方法處理后的地震資料信噪比有較大提高,剖面上的斷點(diǎn)更清晰,斷層的空間組合關(guān)系更明確,解釋結(jié)果的可靠性更高。
斷層解釋 結(jié)構(gòu)導(dǎo)向平滑 濾波 梯度結(jié)構(gòu)張量 傾角掃描
1 引言
地震資料中的噪聲會(huì)對(duì)解釋工作造成一定影響,尤其是對(duì)深層地震資料的斷層解釋。因此,有必要對(duì)疊后地震數(shù)據(jù)體進(jìn)行平滑濾波。常規(guī)的平滑濾波方法雖然能夠很好地壓制隨機(jī)噪聲,但是不能避免沿著斷層或其他不連續(xù)體平滑,導(dǎo)致斷層或其他不連續(xù)體的邊界被模糊,從而對(duì)斷層解釋造成不利影響。
人們對(duì)保持構(gòu)造信息和增強(qiáng)邊界信息的地震數(shù)據(jù)平滑濾波進(jìn)行了深入研究。Weichert[1-3]將擴(kuò)散方程引入圖像平滑中,提出了非線性擴(kuò)散濾波、各向異性擴(kuò)散濾波和相干增強(qiáng)擴(kuò)散濾波。隨后,H?cker等[4]、Fehmers等[5]將 Weichert的方法引入地震數(shù)據(jù)處理,推出了一種結(jié)構(gòu)導(dǎo)向?yàn)V波方法。在此基礎(chǔ)上,Hale[6]研究了實(shí)現(xiàn)方便、計(jì)算效率高的結(jié)構(gòu)導(dǎo)向平滑方法;后來 Hale[7,8]提出了改進(jìn)的結(jié)構(gòu)導(dǎo)向雙邊濾波方法,并將其應(yīng)用于地震圖像處理。Al-Bin Hassani等[9]研究了基于多窗口分析的保護(hù)邊界信息的平滑濾波方法。Wang等[10]采用基于可靠估計(jì)反射方位和邊界的構(gòu)造約束保邊濾波法,通過掃描主頻分頻數(shù)據(jù)體估算反射視傾角和相干值,受噪聲影響更小,估算精度更高。分頻段選擇性濾波[11,12]、多窗口平滑 等方法[9,11]提高 了濾波 的準(zhǔn)確性。劉洋等[13]提出了局部相關(guān)加權(quán)中值濾波技術(shù),并用于疊后隨機(jī)噪聲衰減處理,可以很好地保護(hù)地震資料中的斷層等信息。趙明章等[14]利用構(gòu)造導(dǎo)向?yàn)V波技術(shù)識(shí)別復(fù)雜斷塊圈閉,取得了較好的地質(zhì)效果。宋建國(guó)等[15]提出了基于結(jié)構(gòu)導(dǎo)向的梯度屬性邊緣檢測(cè)技術(shù),能準(zhǔn)確地識(shí)別小斷層、微裂縫,可以作為一種地震資料精細(xì)解釋工具。Song等[16,17]研究了基于傾角導(dǎo)向Facet模型曲面擬合的邊緣檢測(cè)方法,并用于斷層識(shí)別。劉洋等[18]提出了基于非平穩(wěn)相似性系數(shù)的構(gòu)造導(dǎo)向?yàn)V波及斷層檢測(cè)方法。蔡涵鵬等[19]提出了基于多窗口相干性的傾角導(dǎo)向主分量濾波。Cai等[20]研究了邊界和振幅特性保持的自適應(yīng)噪聲衰減方法。尹川等[21]提出了傾角控制的構(gòu)造導(dǎo)向?yàn)V波方法。Liu等[22]研究了基于二維希爾伯特變換的地震傾角求取方法,并用于隨機(jī)噪聲衰減處理。
對(duì)于構(gòu)造較平緩的區(qū)域,易于提取傾角、方位角等數(shù)據(jù),容易實(shí)現(xiàn)傾角導(dǎo)向平滑;對(duì)于復(fù)雜構(gòu)造區(qū)域,很難精確求取傾角、方位角等信息,導(dǎo)致傾角導(dǎo)向平滑方法的應(yīng)用效果不佳。為此,本文結(jié)合前人研究成果,研究了針對(duì)復(fù)雜構(gòu)造的深層地震資料的結(jié)構(gòu)導(dǎo)向平滑方法,對(duì)比了傾角導(dǎo)向平滑與結(jié)構(gòu)導(dǎo)向平滑方法的實(shí)際應(yīng)用效果。結(jié)果表明,結(jié)構(gòu)導(dǎo)向平滑方法對(duì)地震資料信噪比的要求較低,放寬了該方法的適用條件,且更有利于提取高品質(zhì)的相干體屬性,而傾角導(dǎo)向平滑方法對(duì)地震資料的信噪比要求則很高。
2 理論基礎(chǔ)
結(jié)構(gòu)導(dǎo)向平滑和相干濾波的平滑系數(shù)取決于地震圖像中相關(guān)構(gòu)造的方位,可以通過傾角、方位角掃描獲得所需要的方位信息。但是地下地質(zhì)體的構(gòu)造形態(tài)是未知的,在缺乏先驗(yàn)信息約束的情況下,傾角、方位角掃描的計(jì)算量非常大,并且精度不高。
地震圖像的梯度結(jié)構(gòu)張量可以提供構(gòu)造的方位信息,其求取完全依賴于地震數(shù)據(jù),具有較強(qiáng)的客觀性。梯度結(jié)構(gòu)張量的特征向量可以用于設(shè)計(jì)結(jié)構(gòu)導(dǎo)向平滑濾波器,可以確保平滑過程沿著局部線性或者平面構(gòu)造進(jìn)行,而不需要跨越上述構(gòu)造。
2.1 梯度結(jié)構(gòu)張量
對(duì)于三維地震圖像,每個(gè)采樣點(diǎn)的梯度結(jié)構(gòu)張量是一個(gè)半正定對(duì)稱矩陣,可以表示為[23]
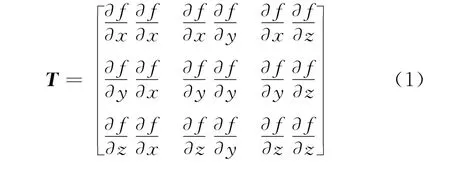
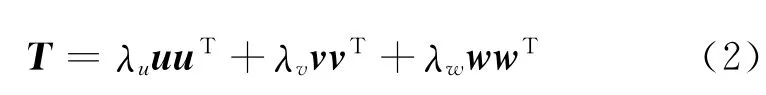
式中:λu、λv和λw為特征值;u、v和w分別表示對(duì)應(yīng)的特征向量,其中u表示與構(gòu)造方向垂直的分量,w表示與構(gòu)造方向平行的分量。梯度結(jié)構(gòu)張量矩陣為結(jié)構(gòu)導(dǎo)向平滑提供窗口方向和窗口大小兩個(gè)參數(shù)。
2.2 結(jié)構(gòu)導(dǎo)向平滑
結(jié)構(gòu)導(dǎo)向平滑方法的理論基礎(chǔ)是物理學(xué)擴(kuò)散過程[5]。擴(kuò)散通量的表達(dá)式由菲克定律給出

式中:j為擴(kuò)散通量;f為地震振幅的梯度;D為擴(kuò)散張量,它是一個(gè)對(duì)稱的半正定張量矩陣。
由于擴(kuò)散過程中質(zhì)量是守恒的,因此式(3)可以用連續(xù)性方程表示為

式中τ表示擴(kuò)散時(shí)間(不同于地震記錄的走時(shí))。將式(3)代入式(4),可以得到擴(kuò)散方程
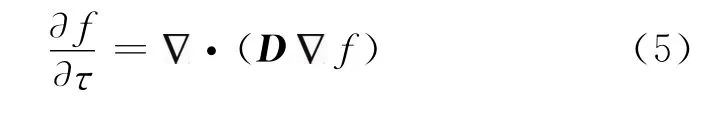
在構(gòu)建擴(kuò)散方程中的擴(kuò)散張量D時(shí),采用地震圖像的梯度結(jié)構(gòu)張量矩陣T的特征向量。
對(duì)于式(5),Hale[6]提出了一種改進(jìn)的偏微分方程形式
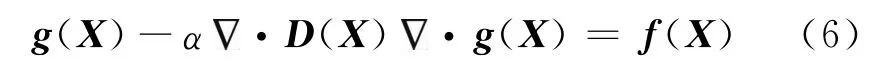
式中:f(X)(X=(x,y,z)為空間坐標(biāo))為輸入的地震圖像;g(X)為輸出的平滑圖像;D(X)為平滑后的張量矩陣;α為常量,表示平滑系數(shù),特別地,當(dāng)α=0時(shí),g(X)=f(X),表明圖像沒有經(jīng)過平滑。
式(6)的一維形式可以表示為[6]

采用Z變換,可以得到偏導(dǎo)數(shù)的雙線性變換形式[6]
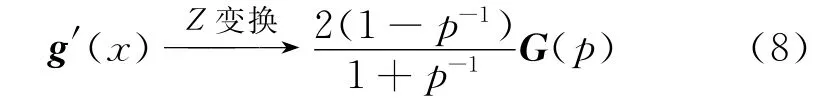
式中:g′(x)為g(x)的偏導(dǎo)數(shù);G(P)為g(x)的Z變換[6],即
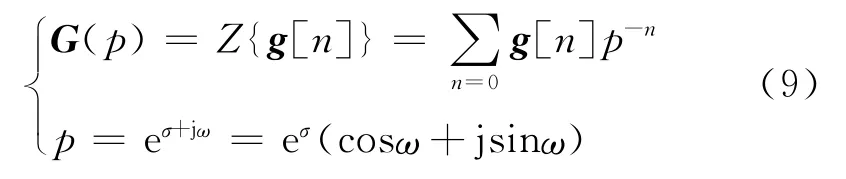
式(8)的等價(jià)形式為[6]

式(7)的Z變換形式為[6]
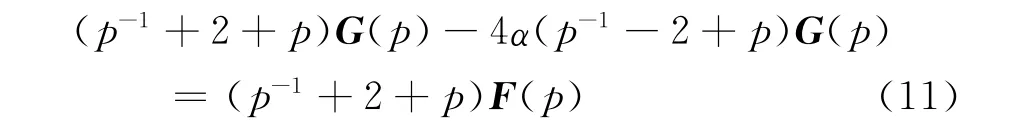
式中F(P)為f(x)的Z變換。式(11)的等價(jià)形式為
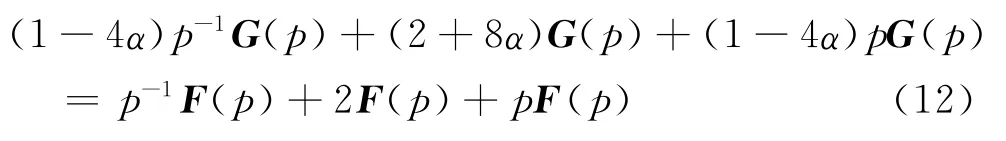
與之對(duì)應(yīng)的有限差分近似式為[6]
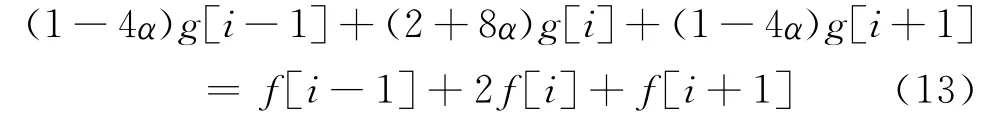
式中i=0,1,…,N-1,N表示采樣點(diǎn)數(shù)。
對(duì)于二維或三維地震數(shù)據(jù),可以定義向量F=f[i1,i2,…,in]表示n維輸入圖像f(X),定義向量g[i1,i2,…,in]表示輸出的平滑圖像g(X),則式(6)可以表示為[6]
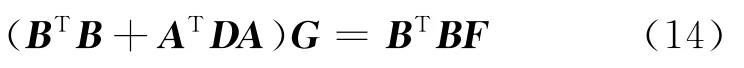
式中:稀疏矩陣A和B表示有限差分近似;D為不含零元素的系數(shù)矩陣,與式(6)中的張量矩陣D(X)對(duì)應(yīng),控制平滑方向,在結(jié)構(gòu)導(dǎo)向平滑中采用D=vvT+wwT構(gòu)建擴(kuò)散張量。
采用基于梯度結(jié)構(gòu)張量的結(jié)構(gòu)導(dǎo)向平滑方法處理實(shí)際資料的具體流程如下:
(1)利用原始地震數(shù)據(jù)求取每個(gè)采樣點(diǎn)在x、y、z(或t)方向的導(dǎo)數(shù),并求取梯度結(jié)構(gòu)張量矩陣T。
(2)通過特征分解求取梯度結(jié)構(gòu)張量矩陣T的特征向量,并構(gòu)建擴(kuò)散張量矩陣D。
(3)將擴(kuò)散張量矩陣D代入式(14),采用共軛梯度迭代法求解該方程,求得的解即為平滑后的圖像。
3 實(shí)際應(yīng)用
為了檢驗(yàn)結(jié)構(gòu)導(dǎo)向平滑方法的效果,針對(duì)XJ地區(qū)的地震資料開展了應(yīng)用研究。研究區(qū)的主要目的層系集中在古近系,圖1為目標(biāo)區(qū)的原始地震剖面。由圖可見,深層地震資料的品質(zhì)較差,信噪比較低,斷面不清晰,斷層解釋難度較大。圖2是與圖1相對(duì)應(yīng)的相干體剖面。由圖可見,目標(biāo)區(qū)斷裂發(fā)育,大斷裂附近有幾條伴生的小斷裂,受地震資料品質(zhì)的限制,斷裂的空間展布特征不明顯,斷層組合識(shí)別難度極大。

圖1 原始地震剖面
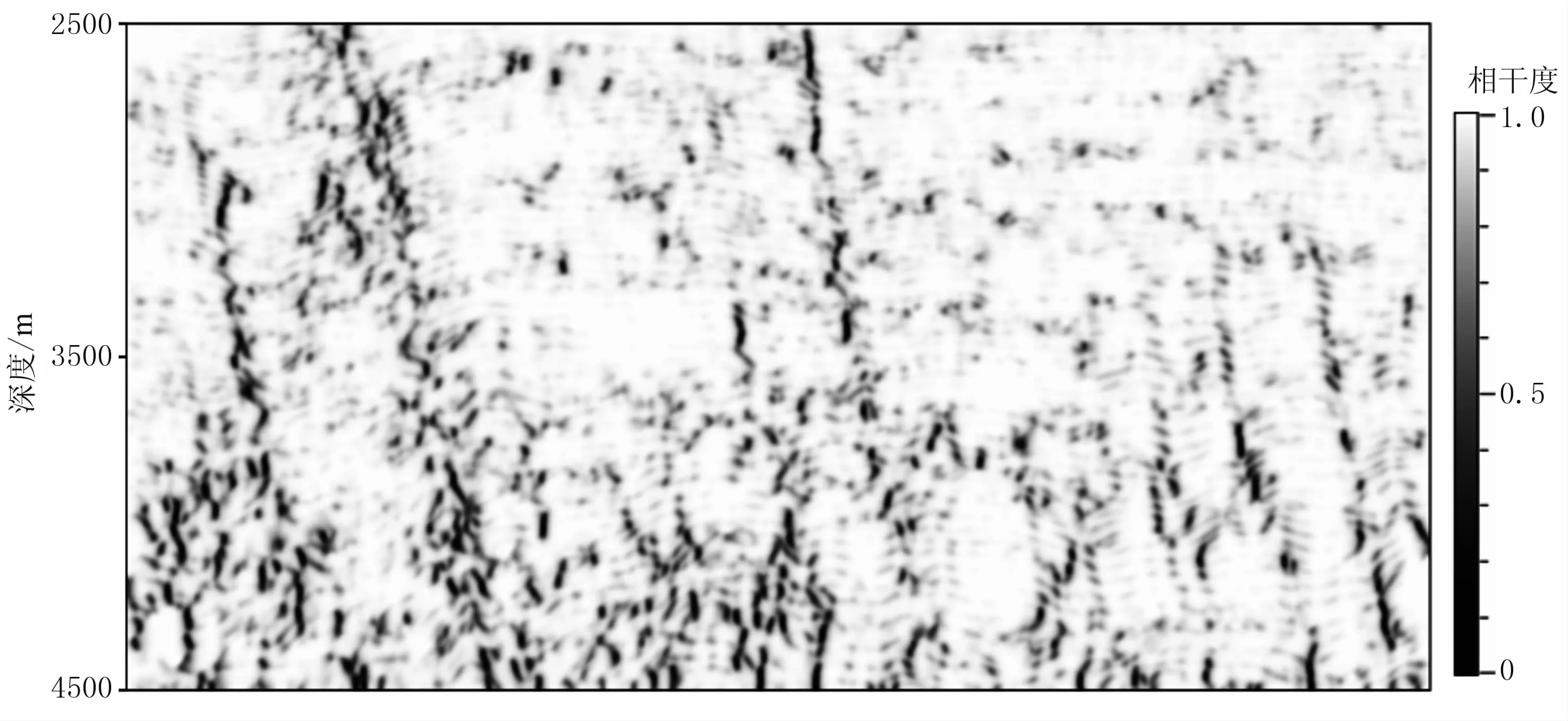
圖2 相干體剖面
為了厘清目標(biāo)區(qū)的斷裂體系發(fā)育特征,同時(shí)檢驗(yàn)結(jié)構(gòu)導(dǎo)向平滑方法的有效性,本文分別采用傾角導(dǎo)向平滑、結(jié)構(gòu)導(dǎo)向平滑方法對(duì)原始地震資料進(jìn)行處理。圖3為傾角屬性剖面。由圖可見,傾角變化較大的區(qū)域基本對(duì)應(yīng)斷裂發(fā)育區(qū)。圖4為梯度結(jié)構(gòu)張量的特征向量,其平行于原始地震剖面的構(gòu)造方向,為結(jié)構(gòu)導(dǎo)向平滑提供了方向約束。圖5為經(jīng)傾角導(dǎo)向平滑和結(jié)構(gòu)導(dǎo)向平滑處理的地震剖面。由圖可見,相對(duì)于原始地震剖面,經(jīng)傾角導(dǎo)向平滑(圖5a)和結(jié)構(gòu)導(dǎo)向平滑(圖5b)處理的地震剖面的信噪比都有所提高,但是后者比前者的效果更佳,對(duì)噪聲的壓制能力更強(qiáng),尤其是在斷層附近,幾乎沒有噪聲的干擾,斷點(diǎn)非常清晰,有利于斷層解釋。
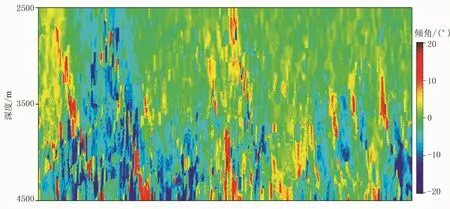
圖3 傾角屬性剖面

圖4 梯度結(jié)構(gòu)張量的特征向量
圖6為對(duì)傾角導(dǎo)向平滑和結(jié)構(gòu)導(dǎo)向平滑處理地震數(shù)據(jù)提取的相干體剖面。由圖可見:傾角導(dǎo)向平滑相干體剖面對(duì)斷層的顯示不清晰,不能準(zhǔn)確地描述斷層的發(fā)育特征(圖6a橢圓處);結(jié)構(gòu)導(dǎo)向平滑相干體剖面對(duì)斷層的刻畫更精細(xì),斷層的空間組合關(guān)系明確(圖6b橢圓處),大大降低了人工解釋的難度。產(chǎn)生這種現(xiàn)象的原因是:①在實(shí)際應(yīng)用中,地下構(gòu)造的傾角、方位角是未知的,采用傾角掃描法求取傾角、方位角屬性的過程是按照一定的步長(zhǎng)進(jìn)行尋優(yōu)的,這種做法會(huì)遺漏傾角、方位角的真實(shí)值,尤其是在復(fù)雜區(qū)域,很難準(zhǔn)確求取真實(shí)的傾角、方位角;②傾角導(dǎo)向平滑方法對(duì)傾角、方位角的精度要求很高,當(dāng)?shù)卣鹳Y料信噪比較低時(shí),很難精確提取傾角、方位角屬性。
4 結(jié)束語
基于梯度結(jié)構(gòu)張量的結(jié)構(gòu)導(dǎo)向平滑方法能夠提高地震資料的信噪比,在壓制噪聲的過程中能有效地保留斷層等不連續(xù)性信息,避免了常規(guī)平滑方法容易引起斷點(diǎn)模糊的缺點(diǎn)。應(yīng)用結(jié)果表明:相對(duì)于傾角導(dǎo)向平滑方法,結(jié)構(gòu)導(dǎo)向平滑方法對(duì)地震資料信噪比的要求較低,放寬了該方法的適用條件;對(duì)于空間組合關(guān)系復(fù)雜的斷裂帶,經(jīng)結(jié)構(gòu)導(dǎo)向平滑處理得到的剖面的斷點(diǎn)更加明確,更有利于人工解釋,且由結(jié)構(gòu)導(dǎo)向平滑處理的地震數(shù)據(jù)提取的相干體屬性品質(zhì)更高,斷層空間組合關(guān)系更加明確。

圖5 經(jīng)傾角導(dǎo)向平滑(a)和結(jié)構(gòu)導(dǎo)向平滑(b)處理的地震剖面
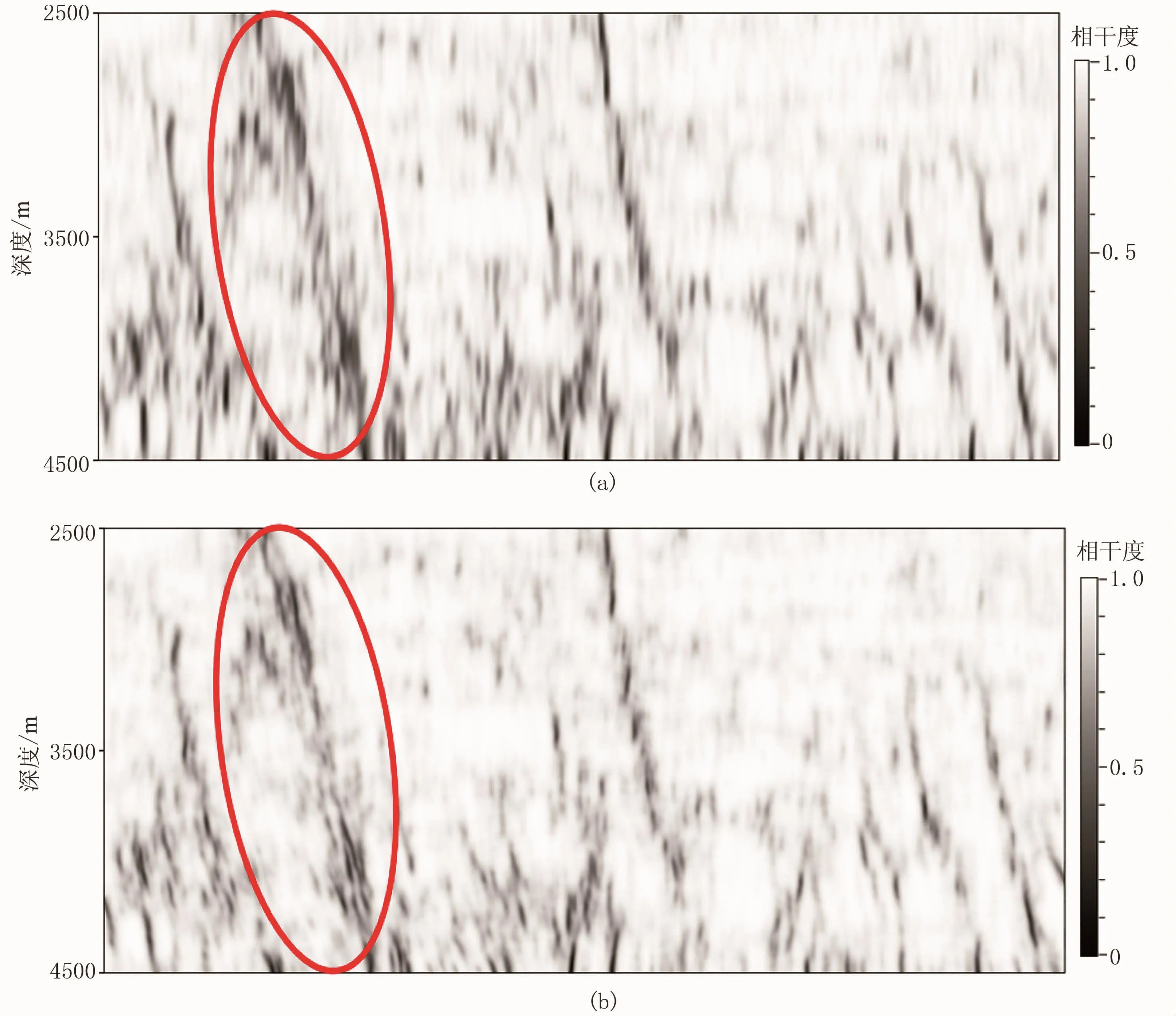
圖6 對(duì)傾角導(dǎo)向平滑(a)和結(jié)構(gòu)導(dǎo)向平滑(b)處理的地震數(shù)據(jù)提取的相干體剖面
[1] Weickert J.A review of nonlinear diffusion filtering.Lecture Notes in Computer Science,Springer,1997,1252:3-28.
[2] Weickert J.Anisotropic Diffusion in Image Processing.Teubner Verlag,1998.
[3] Weickert J.Coherence-enhancing diffusion filtering.International Journal of Computer Vision,1999,31(2):111-127.
[4] H?cker C F W,F(xiàn)ehmers G C.Fast structural interpretation with structure-oriented filtering.The Leading Edge,2002,21(3):238-243.
[5] Fehmers G C,H?cker C F W.Fast structural interpretations with structure-oriented fltering.Geophysics,2003,68(4):1286-1293.
[6] Hale D.Structure-oriented smoothing and semblance.CWP Report 635,2009.
[7] Hale D.Structure-oriented bilateral filtering.CWP Report 695,2011.
[8] Hale D.Structure-oriented bilateral filtering of seismic images.SEG Technical Program Expanded Abstracts,2011,30:3596-3600.
[9] Al-Bin Hassan N M,Luo Yi,Al-Faraj M N.3D edgepreserving smoothing and applications.Geophysics,2006,71(4):P5-P11.
[10] Wang Jun,Chen Yuhong and Qiao Yulei.Structureoriented edge-preserving smoothing based on accurate estimation of orientation and edges.Applited Geophysics,2009,6(4):367-376.
[11] Marfurt K J.Robust estimates of 3D reflector dip and azimuth.Geophysics,2006,71(4):29-40.
[12] Al-Dossary S,Marfurt K J.Lineament-preserving filtering.Geophysics,2007,72(1):P1-P8.
[13] 劉洋,王典,劉財(cái)?shù)?局部相關(guān)加權(quán)中值濾波技術(shù)及其在疊后隨機(jī)噪聲衰減中的應(yīng)用.地球物理學(xué)報(bào),2011,54(2):358-367.Liu Yang,Wang Dian,Liu Cai et al.Weighted median filter based on local correlation and its application to poststack random noise attenuation.Chinese Journal of Geophysics,2011,54(2):358-367.
[14] 趙明章,范雪輝,劉春芳等.利用構(gòu)造導(dǎo)向?yàn)V波技術(shù)識(shí)別復(fù)雜斷塊圈閉.石油地球物理勘探,2011,46(增刊1):128-133.Zhao Mingzhang,F(xiàn)an Xuehui,Liu Chunfang et al.Complex fault-block traps identification with structure-oriented filter.OGP,2011,46(S1):128-133.
[15] 宋建國(guó),孫永壯,任登振.基于結(jié)構(gòu)導(dǎo)向的梯度屬性邊緣檢測(cè)技術(shù).地球物理學(xué)報(bào),2013,56(10):3561-3571.Song Jianguo,Sun Yongzhuang,Ren Dengzhen.Edge detection technique based on structure-directed gradient attribute.Chinese Journal of Geophysics,2013,56(10):3561-3571.
[16] Song Jianguo,Mu Xing,Li Zhe et al.A faults identification method using dip guided facet model edge detector.SEG Technical Program Expanded Abstracts,2012,31:1-5.
[17] Song Jianguo,Mu Xing,Li Zhe et al.Fault identification using dip-guided facet model edge detector.Interpretation,2014,2(2):T89-T101.
[18] 劉洋,王典,劉財(cái)?shù)?基于非平穩(wěn)相似性系數(shù)的構(gòu)造導(dǎo)向?yàn)V波及斷層檢測(cè)方法.地球物理學(xué)報(bào),2014,57(4):1177-1187.Liu Yang,Wang Dian,Liu Cai et al.Structure-oriented filtering and fault detection based on nonstationary similarity.Chinese Journal of Geophysics,2014,57(4):1177-1187.
[19] 蔡涵鵬,賀振華,李亞林等.基于多窗口相干性的傾角導(dǎo)向主分量濾波.石油地球物理勘探,2014,49(3):486-494.Cai Hanpeng,He Zhenhua,Li Yalin et al.Dip-steering principal component filter using multi-window coherence scanning and interpolation.OGP,2014,49(3):486-494.
[20] Cai Hanpeng,He Zhenhua,Li Yalin et al.An adaptive noise attenuation method for edge and amplitude preservation.Applied Geophysics,2014,11(3):289-300.
[21] 尹川,杜向東,趙汝敏等.基于傾角控制的構(gòu)造導(dǎo)向?yàn)V波及其應(yīng)用.地球物理學(xué)進(jìn)展,2014,29(6):2818-2822.Yin Chuan,Du Xiangdong,Zhao Rumin et al.Dip steered structure oriented filter and its application.Progress in Geophysics,2014,29(6):2818-2822.
[22] Liu Cai,Chen Changle,Wang Dian et al.Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation.Applied Geophysics,2015,12(1):55-63.
[23] Randen T,Monsen E,Signer C et al.Three-dimensional texture attributes for seismic data analysis.SEG Technical Program Expanded Abstracts,2000,19:668-671.

P631
A
10.13810/j.cnki.issn.1000-7210.2017.01.020
問雪,陳雪芳,陳勝紅,孟大江,唐明銘,吳成.利用結(jié)構(gòu)導(dǎo)向平滑方法解釋斷層.石油地球物理勘探,2017,52(1):146-151.
1000-7210(2017)01-0146-06
*廣東省深圳市南山區(qū)后海濱路(深圳灣段)3168號(hào)中海油大廈A座2008室,518054。Email:wenxue2@cnooc.com.cn
本文于2016年2月23日收到,最終修改稿于同年11月17日收到。
(本文編輯:劉勇)
問雪 助理工程師,1988年生;2011年獲長(zhǎng)安大學(xué)勘探技術(shù)與工程專業(yè)學(xué)士學(xué)位;2014年獲中國(guó)石油大學(xué)(華東)地球探測(cè)與信息技術(shù)專業(yè)碩士學(xué)位;現(xiàn)就職于中海石油(中國(guó))有限公司深圳分公司研究院,主要從事地震解釋、儲(chǔ)層預(yù)測(cè)等方面研究。

