山區高速公路高填方路堤安全風險評價研究

郭曉魁

（山西省公路工程質量檢測中心，山西 太原 030006）

0 引言

20世紀中后期，我國經濟發展進入前所未有的快車道。同時，高速公路的建設也得到了蓬勃發展，全國高速公路總里程也居于世界前列[1]。預計十三五時期，我國西部地區路網覆蓋將更加全面、各項基礎設施建設將更加完善，運輸服務水平將得到顯著提升[2]。由于受到地形地貌影響，山區高速建設過程中會有大量的高填方路堤施工，同時由于各方面復雜因素的交叉作用，路堤變形過大和失穩破壞的工程風險問題較多。因此，對于多山地區的此類路堤安全風險評價模型具有相當大的研究價值，并以此來指導山區高速公路等地高填方路堤的實際工程，對路堤的風險防范與管理實現動態化可預測化管理，具有非常重要的理論價值和現實意義。

“風險分析”是在第一次世界大戰后，由于戰爭對于城市的破壞嚴重，在以德國為代表城市重建工作中應運而生的，1931年美國首次提出“風險管理”理念，風險管理和保險問題便由此被大家所漸漸熟知。在20世紀中葉西方各國對于風險分析研究開展了大量研究，在工程中主要集中在邊坡的穩定性評估的風險評價體系，直到2000年，A.Uromeihy and M.R.Mahdavifar[3]通過建立考慮多種影響因素的模糊集理論模型，計算潛在風險指標值。我國從20世紀80年代通過對結構工程和水利水電工程的風險決策，開啟了我國的風險分析研究。吳世偉[4]、劉玉恒[5]、汪敏[6]、陳祖煜[7]等人先后對于邊坡的穩定風險問題進行了深入研究，并各自提出了相應的評價方法。但通過國內的研究現狀可以看出，不同學者的研究角度、研究重點不同，因此，災害風險分析研究當前還不是很成熟，分析理論還不是很健全。特別是對于高填方路堤方面的的研究還很欠缺，相關理論方面的研究也比較欠缺，實踐應用沒有完全實現。本文主要介紹以突變理論為基礎的風險綜合評價模型，分別通過理論推導和在實際工程的應用來說明上述方法的合理性。

1 理論分析

當前對于高填方路堤的失穩風險控制還不是很完善，尤其對于一些不確定性因素引起的風險仍然采用不同施工技術來控制，對于風險分析的理論研究還很匱乏。在實際工程中，路堤失穩風險在施工進行中時有發生，輕則財產損失，重則人員傷亡。然而，高填方路堤的失穩破壞的表現形式大多數為一種非線性動力學的機制。因此，對于此類問題可用突變理論給予分析。突變理論主要運用拓撲學和奇點理論對于不連續現象進行研究。本章利用此理論在非單一目標決策上的優越性這一特征，將其與綜合評價相結合，以路堤施工現場檢測資料為依托建立了多層次評價體系，對承赤高速公路高填方路堤現場施工過程中的安全進行風險評價，通過分析監測數據的變化，可以分析路堤安全穩定狀態及變化趨勢。

突變數學由法國科學家雷內·托姆（Rene Thom）于70年代創建，作為一門研究突變的新的數學形式，其建立在微積分、奇點理論、拓撲動力學等數學理論的基礎上，對于不連續變化、突變現象等問題進行專門研究[8]。主要方法是以一個系統的勢函數為基礎，將其邊界點進行歸類，以便于探索不同類型邊界點臨近位置的間斷性變化特點，因而總結出幾個不同形式的初等突變模型。其特點是首先通過多層次矛盾拆分的方法將所分析系統的評價指標進行分解，再通過歸一公式對上述分解后的各指標進行整合并將其量化運算，最終得出一個參數，即為總的隸屬函數，來對整個系統進行綜合評價[9]。該方法的優點是在考慮各因子之間相對重要度時沒有采用權重的分配方法，從而使評價分析減少了人為主觀性而又不缺乏科學性，因此更符合實際。

雷內·托姆最初歸納了7個突變模型，后來又引申為11個，表1為最初的7個突變模型及勢函數。

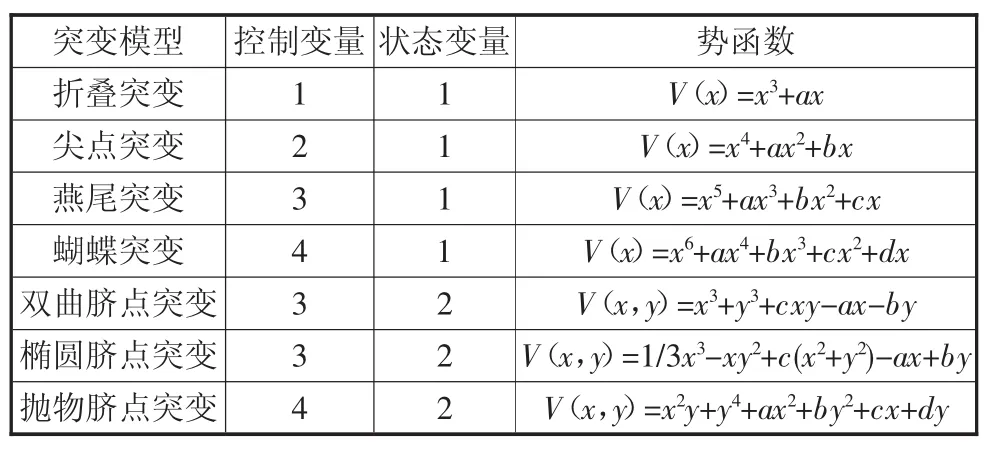
表1 突變模型及其勢函數

下面簡單介紹突變級數法的實施方案[9]。

1.1 評價體系建立

對評判系統或總指標按照某一原則進行分解，得到由若干個評價因子組成的多層次評價體系，按照重要程度的先后順序將所包含的評價因子排成樹狀結構。具體做法是通過逐層分解的方法將評價目標分解到可量化指標即可以停止。這是因為一般上層指標不很明確，較難定量地進行分析，因此需將這些上層指標進行分解得到能夠定量分析的具體指標。同時需注意對單個上層因子分解后得到的下層因子的個數不要超過4個，這是因為突變模型中的控制變量最多為4個，這樣才能用到匹配的突變模型。

1.2 突變模型

在確定了評價體系結構后，根據每一層評價因子的個數確定與之匹配的突變模型，如表1中所示。通常我們用到的突變系統類型主要為3種。這3種模型的結構示意如圖1所示，相對應的模型函數表示為式（1）～式（3）。

尖點突變模型：

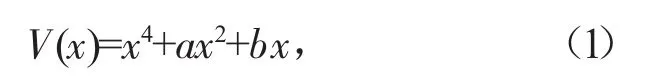
燕尾突變模型：

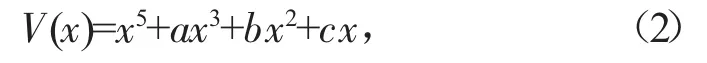
蝴蝶突變模型：

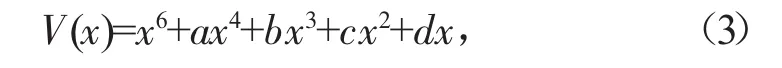
式中：V(x)為某一系統的勢函數；x 為狀態變量；a、b、c、d為狀態變量系數，表示該狀態變量的控制變量。有兩個相互矛盾的主體存在于模型勢函數中，其分別為狀態變量和控制變量，并且相互作用影響又存在于各控制變量之間。

圖1 3種突變模型示意圖

1.3 歸一公式確定

對應的歸一公式可通過對模型的分歧集方程進行演算求得。V(x)設為系統勢函數，由突變理論可得出一平衡曲面可由其全部邊界點組成，通過對上述函數求一階導數后可得到曲面方程，即V′(x)=0；通過求二階導數即可以等到相應的奇點集合，即V″(x)=0；而后通過聯立求解上述兩個方程后，即可得出突變系統的分歧點集方程。該方程說明系統的各控制變量在滿足上述條件時就會發生突變。最后模型的歸一公式經過計算得到式（4）～式（6）。

尖點突變模型歸一公式為：

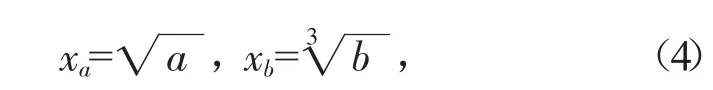
燕尾突變模型歸一公式為：

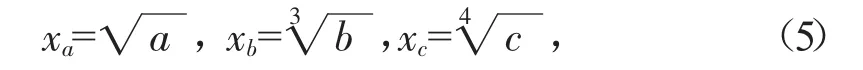
蝴蝶突變模型歸一公式為：

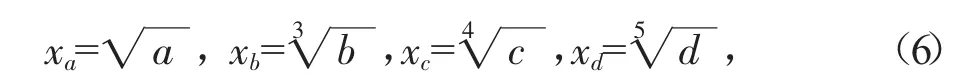
式中：xa、xb、xc、xd分別為各式對應于 a、b、c、d時x的值。

1.4 綜合評價時對于歸一公式的使用條件

根據評價體系中每一層評價因子的個數確定相匹配的初等突變模型，并從最底層的評價因子開始利用歸一公式進行評判。在評判中應遵循3種評價原則：互補原則、非互補原則、過閥值后互補原則。

利用歸一公式對上層評價因子分解后的各個下層評價因子計算，得到相應的值，并根據因子之間的關系及對上層因子的影響分別采用上述3種原則之一。當某一級下層的各個因子之間無條件相互補充不足，使x值平均值較高，這時即滿足了互補原則，突變級數可直接取評價因子歸一后的“平均值”；當這些因子不能相互之間補充對方的不足，即符合了非互補原則，因而評價因子歸一后按照大中取小的方案獲得它的“最小值”，在此條件下對于分歧方程予以滿足，最終發生質的改變；各指數及其x值在符合特定的閥值條件時才能相互補充，此時即符合了過閥值后的互補原則。

2 現場監測方案

承赤高速主線是蒙冀界至承德，修成后計劃通車里程111.362 km。工程修建通車后，對于完善河北省高速公路網主骨架乃至于全國高速公路網都有非常重要的意義。通過對承赤高速公路現場的多次踏勘，將此次監測的場地選擇在承赤高速第七標段和第九標段的高填方路段，其中第七標段路堤平均高度為18.0 m，第九標段的兩個路堤分別為12.65 m和14.7 m。根據研究目的，確定本次監測的主要內容有：道路路基基本沉降量的監測、土體承受載荷應力狀態的監測、施工土體側向位移的監測。

根據現場場地的實際情況，為滿足高度要求，同時便于觀測，將承赤高速第七合同段高填方監測段選定在020涵洞附近區域。分別對于上述的三方面主要檢測內容進行檢測，對于沉降、側向位移以及承載力分別設置了3個、2個和12個監測點。其示意圖如圖2所示。

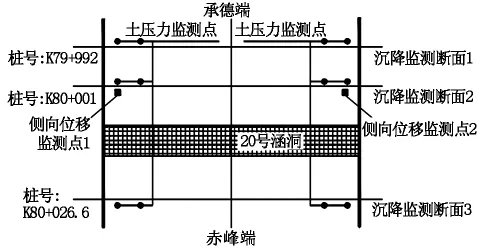
圖2 監測項目設置平面布置示意圖

由于施工過程中的監測數據作為其穩定性控制的主要依據，因此采用燕尾突變模型對首層指標進行評價，主控參量為監測數據（B），邊坡形態（C），其次，填料性質（D）的影響放在最后，因為該評價體系是以施工期監測數據的變化為主要研究對象，監測數據為主要依據，因此填料的性質變化影響最小。其中側向變形（B1）、豎向位移（B2）、土壓力（B3）等作為下層指標。側向變形和豎向位移是路堤穩定最直觀的因子，路堤邊坡的穩定狀態與側向變形的速率息息相關，而路堤整體的穩定性與路堤的沉降（豎向位移）密不可分。土的壓力變化也可以反映施工填筑速率的大小及地基土的受力狀態。路堤穩定性發現問題時上述3項指標隨機會出現異常。對于高填方路堤的邊坡穩定是以側向變形為主，豎向位移次之，土壓力是為了了解地基的情況故影響程度最小，這3項因子采用燕尾突變模型。對于高填方路堤的邊坡是在設計階段確定的邊坡坡度和路堤高度，且坡度一般按照相關規范選取，因為高度是隨填筑過程而增加的，坡度變化較小，因此邊坡形態對路堤的安全影響坡高（C1）大于坡角（C2），這兩項因子采用尖點突變模型。路堤填土的特性對路堤影響主要是以黏聚力（D1）、內摩擦角（D2）來體現的，通過已有的多數研究顯示，黏聚力是影響路堤土穩定性的主要因素，其次為內摩擦角，所以這兩項因子運用尖點突變模型。

3 實例計算與分析

限于篇幅原因，本文重點對承赤高速第七合同段的高填方路堤施工期的數據進行計算分析。同時由于檢測數據量較大，且為了適應本文的計算方法，選擇沉降檢測斷面2范圍的監測項目所獲取的監測數據為主要分析對象。因為該路堤斷面基本為對稱結構，故選擇一半的數據作為參考量。本文是以施工期的路堤安全風險評價為研究對象，隨著施工的進度進行連續的評價分析，因此需要按照填筑的時間序列進行分析。為滿足各監測項目在時間上的一致，選取合適的時間點進行分析。通過分析監測資料，可以分析路堤的變形情況，推斷變化趨勢及不利的結構面位置，從而反饋到風險評價中[10]。故選取的時間段序列為 Ⅰ ：2012-07-19—2012-07-23； Ⅱ ：2012-07-23—2012-07-28；Ⅲ：2012-07-28—2012-08-02。

3.1 評價因子初始值選取

3.1.1 測斜管數據分析

為了便于直觀地分析測斜管上監測數據的變化，對各測點的水平位移時間變化的分析選取奇數點的監測值，并繪制隨時間推移水平位移變化曲線如圖3，其中監測日期以橫坐標表示。其中測斜管水平位移監測數據變化曲線如圖4。

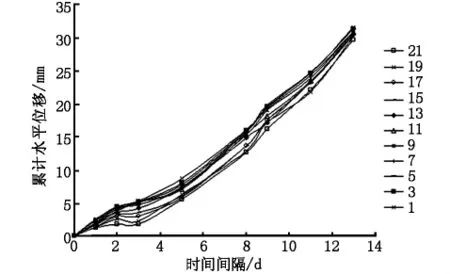
圖3 各測點水平位移變化

從圖3、圖4中不難看出伴隨測斜管深度和填筑高度的不斷增加，累計水平位移也呈增大趨勢，因為測斜管的安置位置是在路堤邊坡上，因此可以反映出路堤底部的側移要大于上部區域。各測點的位移增長率基本為線性增長，在填筑期的位移增長率沒有減小的趨勢。

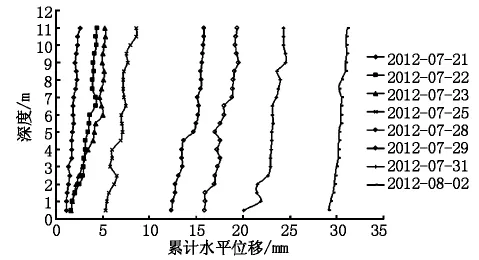
圖4 累計水平位移變化

為了便于分析變形速率的變化，將Ⅰ、Ⅱ、Ⅲ時間段的數值變化速率進行了分析，發現變形速率較大的監測點主要集中在路堤底部區域，還有零散地分布于中部的測點。為了方便對比，均取底部2 m區域的最大的3個變形速率的平均值作為評價因子的初始值。因此計算出結構變形速率分別為：Ⅰ期間vⅠ=1.56 mm/d，Ⅱ期間 vⅡ=2.19 mm/d，Ⅲ期間 vⅢ=3.21 mm/d。

3.1.2 沉降管數據分析

根據求得的測點1、測點2、測點3在Ⅰ期間的變形速率分別為 1.99 mm/d、2.65 mm/d、3.35 mm/d；Ⅱ期間的變形速率為 1.15 mm/d、2.65 mm/d、3.23 mm/d；Ⅲ期間的變形速率為 1.33 mm/d、1.51 mm/d、1.99 mm/d。從中可以看出路堤斷面對稱軸附近的沉降速率為最大，選取測點3的變形速率作為豎向變形因子的初始值進行評價，即變形速率分別為 vⅠ=3.35 mm/d，vⅡ=3.23 mm/d，vⅢ=1.99 mm/d。

3.1.3 土壓力數據分析

根據求得在Ⅰ期間1、2兩測點的土壓力變化速率分別為9.135 kPa/d、9.937 kPa/d；Ⅱ期間的土壓力變化速率為11.775 kPa/d、14.218 kPa/d；Ⅲ期間的土壓力變化速率為2.305 kPa/d、6.927 kPa/d。從中可以看出測點2的變化率較大，選取測點2的變化速率為土壓力因子的初始值進行評價，即 vⅠ=9.937 kPa/d，vⅡ=14.218 kPa/d，vⅢ=6.927 kPa/d。

3.1.4 其他參數分析

通過對工程資料的分析和整理：確定邊坡形態中第Ⅰ、Ⅱ、Ⅲ階段末的坡高分別為13.5 m、16 m、18 m，坡角為30°；填料性質中的內摩擦角約為40°、黏聚力約為29 kPa。

3.2 突變級數值計算

由上文確定了各評價因子的初始值，下面以第Ⅰ階段的路堤突變級數值計算做詳細演示。側向變形速率初始值vⅠ=1.56 mm/d，豎向位移速率初始值vⅠ=3.35 mm/d，土壓力變化速率 vⅠ=9.937 kPa/d，坡高 HI=13.5 m，坡角 ψf=30°，黏聚力 c=29 kPa，內摩擦角φ=40°。

3.2.1 無量綱化計算

對于側向變形速率、豎向位移速率、土壓力變化速率進行無量綱化計算。通過綜合分析并確定：側向變形的區間界限值為x1=1.5 mm/d，x2=4 mm/d，x3=6 mm/d；豎向位移的區間界限值為x1=3 mm/d，x2=5 mm/d，x3=10 mm/d；土壓力的區間界限值為x1=5 kPa/d，x2=15 kPa/d，x3=25 kPa/d。

側向變形：

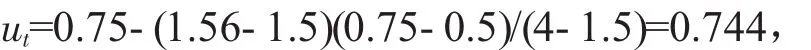
豎向位移：

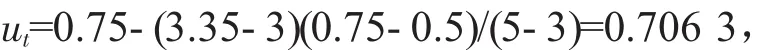
土壓力：

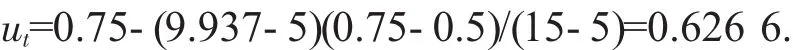
將坡高設為 HI、坡角設為 ψf、黏聚力設為 c、內摩擦角設為φ，分別對上述各量進行無量綱化計算。并綜合分析確定：坡高界限值為x0=0 m，x1=5 m，x2=20 m，x3=40 m；坡角的界限值為 x0=0°，x1=30°，x2=35°，x3=45°；黏聚力的區間界限值為x0=40 kPa，x1=20 kPa，x2=10 kPa，x3=0 kPa；內摩擦角的界限值為 x0=50°，x1=30°，x2=20°，x3=10°。

坡高：

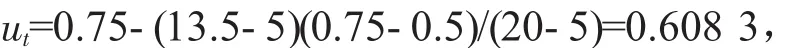
坡角：

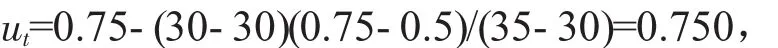
黏聚力：

內摩擦角：

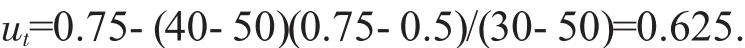
3.2.2 歸一化計算

由前面分析可知側向變形（B1）、豎向位移（B2）、土壓力（B3）形成燕尾突變模型，坡高（D1）和坡角（D2）形成尖點突變模型，黏聚力（C1）、內摩擦角（C2）形成尖點突變模型，進行歸一化計算。

對 于 B1、B2、B3有 ：B1=0.7441/2=0.8625，B2=0.70631/3=0.891，B3=0.62661/4=0.8897，依據“非互補”原則，大中取小，即B=0.8625。

對 于 C1、C2有 ：C1=0.60831/2=0.780，C2=0.751/3=0.9086，依據“非互補”原則，大中取小，即 C=0.780。

對 于 D1、D2有 ：D1=0.88751/2=0.9421，D2=0.62501/3=0.7906，依據“非互補”原則，大中取小，即D=0.7906。。

對于構成燕尾突變模型B、C、D采用燕尾突變的歸一公式：B=0.86251/2=0.9187，C=0.781/3=0.9205，D=0.79061/4=0.9430。依據之前提出的非互補時大中取小的原則，AI=0.9205，即路堤第Ⅰ階段的總突變函數值為0.9205。

同上可求路堤第Ⅱ階段的總突變函數的函數值為0.9083，第Ⅲ階段的總突變函數的函數值為0.8718。

3.3 結果評價

從這3個階段突變值的大小可以看出，施工期路堤的突變值逐漸變小，這說明路堤的安全穩定性在路堤施工的中后期要小于前期施工時。但是各階段的突變值均較大，且現場路堤施工期安全良好，沒有產生滑坡或大裂縫。根據本文的計算方法和界限值的選取，將突變級數值與路堤安全狀態進行分級劃分，分級標準見表2，可依據該準則對高填方路堤存在的安全風險進行評價。通過對其他斷面監測數據的計算分析，突變級數值在0.86～0.93之間，說明本次監測的路堤工程在施工過程中安全性良好，風險等級為Ⅰ級的低風險區域。

表2 高填方路堤施工期安全風險評價表

4 結論

a）將現場監測數據通過突變級數理論進行理論分析與論證，得出了在施工期的高填方路堤安全風險評價模型。確定了側向變形、豎向位移、土壓力、坡高、坡角、黏聚力、內摩擦角等因素為模型的主要評價因子。

b）以突變級數為理論基礎，確定了高填方路堤在施工過程中的風險等級標準為：Ⅰ安全，Ⅱ一般安全，Ⅲ不安全。計算得到了監測路堤在施工期不同階段的突變級數，實現了對路堤施工期各階段的風險評價。通過對路堤施工期變形與穩定性的有限元分析，表明本文監測方案及突變級數風險評價在高填方路堤施工期風險評價的合理性。