一維熱爆炸試驗傳熱的數值模擬

吳 松，陳 均，李明海

(中國工程物理研究院總體工程研究所， 四川 綿陽 621900)

一維熱爆炸試驗傳熱的數值模擬

吳 松，陳 均，李明海

(中國工程物理研究院總體工程研究所， 四川 綿陽 621900)

針對加熱過程所涉及的主要傳熱學問題，分別建立空氣夾層復合傳熱模型和炸藥受熱分解放熱數值模型；計算分析了473K下油浴和空氣浴加熱時系統輻射率、空氣對流換熱系數對RDX、HMX、TATB 3種炸藥熱點火延滯時間的影響。結果表明，473K油浴加熱和空氣浴加熱時RDX分別在151.7s和3372.6s時發生熱點火，表明相同溫度和炸藥，油浴加熱時熱點火延滯時間遠小于空氣浴加熱；空氣浴加熱時，同一種炸藥在相同溫度下，隨系統輻射率的降低，熱點火延滯時間增加；RDX、HMX和TATB炸藥輻射率由0.9降至0.1時，熱點火延滯時間分別增加了180.1%、168.9%和169.3%；相同溫度、相同系統輻射率條件下，對流換熱系數減小，熱點火延滯時間增加。

一維熱爆炸；空氣浴；油浴；輻射率；熱點火延滯時間

引 言

為確定彈體、武器等裝藥結構的性能指標，需加工具有特殊形狀的炸藥試樣進行試驗，分析發生自行爆炸事故的原因是否屬于熱爆炸。同時為了明確裝藥結構在加工、運輸、使用和貯存過程中的熱安全邊界條件，需要進行一維熱爆炸試驗研究[1]。

20世紀國外學者對炸藥的熱安定性進行了一系列研究[2-4]，提出了小藥量爆發點測試方法，獲得了藥柱直徑對熱爆炸臨界溫度的影響規律。隨著炸藥熱起爆研究的深入，原有的評價炸藥熱安定性的方法難以滿足在不同限制條件下成型炸藥柱的熱起爆試驗需求。美國Pantax兵工廠的Schmitz等[5]對ODTX(One dimensional Time-to-Explosion Test)試驗方法進行了大量的研究。20世紀80年代初期，美國能源部(DOE)就已將ODTX列為鈍感高能炸藥(IHE)安全性能檢測的11項重要試驗之一，并在MHSMP-84-22《IHE material qualification tests description and criteria》中詳細規定了試驗件大小、試驗流程及對試驗結果的判定。

MHSMP-84-22中規定了用油浴對炸藥進行加熱，但存在較多安全隱患，如高溫的油易燙傷人；若試驗發生燃燒、爆炸情況，高溫油會加速燃燒，也會引起油飛濺等。因此，近年來許多學者推薦采取空氣浴加熱代替油浴加熱[6]，但兩者加熱方式差別較大，這將導致試驗件溫度從室溫上升到試驗所需溫度的時間不同，從而導致炸藥發生反應的時間不同，影響對試驗結果的判定。

本研究從一維熱爆炸試驗加熱方法入手，分析油浴及空氣浴加熱的異同，并建立熱響應數值模型，計算分析兩種加熱方式時，系統輻射率和空氣對流換熱系數對熱爆炸延滯時間的影響。為一維熱爆炸試驗傳熱數值模擬和相關裝藥結構熱安全研究提供參考。

1 一維熱爆炸試驗

1.1 試驗裝置

一維熱爆炸試驗裝置見圖1[1]。試驗時將裝有炸藥樣品的試驗件放入到預設恒定溫度的加熱器中，樣品受熱發生分解或點火反應。根據發生反應的時間和反應程度，評定該被試炸藥是否滿足鈍感炸藥一維熱爆炸試驗安全性要求。

1.2 加熱方法

MHSMP-84-22《IHE material qualification tests description and criteria》中規定采用油浴對試驗件進行加熱。即將試驗件放置在恒溫(473K或者更高)的油浴中，試樣受熱分解或發生熱點火反應，根據反應時間、反應等級判定該炸藥是否滿足鈍感炸藥要求。由于油浴加熱的劣勢，國內外學者現多采用空氣浴對一維熱爆炸試驗進行研究。空氣浴加熱器和試驗件之間存在環形空腔，兩個壁面之間存在輻射換熱，同時由于空間較大，空氣可在內部流動，存在空氣對流。因此加熱器和試件之間是復合換熱。空氣浴加熱傳熱情況比油浴更復雜，且空氣浴加熱時受熱輻射率和對流換熱系數影響，而油浴加熱不存在此種情況。

2 物理模型的建立

2.1 油浴加熱傳熱模型

油浴加熱示意圖如圖2所示，即將試樣放入恒溫(473～673K)的油浴中，跟油浴直接接觸的套管和炸藥通過熱傳遞接受外部熱量。

油浴加熱只涉及簡單的熱傳遞，邊界條件為第一類熱邊界條件(定溫)[7]。套管外壁接受的熱量可表示為：

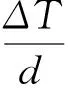
(1)

式中：qcond為傳入到套管的熱量，W；A為熱傳面積，m2；λ為導熱系數，W/(m·k)；ΔT為溫差，K；d為傳熱方向厚度，m。

2.2 空氣浴加熱傳熱模型

空氣浴加熱示意圖如圖3所示，恒溫壁面(473～673K)和套管之間存在空氣夾層，其傳熱包括導熱、對流和輻射3種方式[8]。其中，空氣夾層間殼體兩壁的輻射和空氣對流占主導作用，導熱可以忽略不計。因此，傳入套管壁面的熱量可以表示為：

(2)

式中：q為傳入的總熱量，W；qrad為輻射傳熱量，W；qconv為對流傳熱量，W；σ為斯蒂芬-波爾茲曼常數，5.67×10-8W/(m2·K4)；A為傳熱面積，m2；F為視角系數，1；εh、εs分別為加熱爐和套管壁面的輻射率；Th、Ts分別為加熱爐和套管壁面的溫度，K；hf為對流換熱系數，W/(m2·K)。

由式(2)可知，影響傳入套管容器外壁熱量的主要因素有：加熱爐壁面溫度Th、加熱爐壁面輻射率εh、套管外壁輻射率εs、套管外壁對流換熱系數hf。

加熱爐壁面溫度按實際值取，加熱爐壁面和套管外輻射率分別由各自材料確定，壁面及套管材料為鋁合金，其表面輻射率在0.1～0.2之間(若經過拋光，其表面輻射率更低)。而加熱爐由于會多次使用，炸藥受熱分解或反應產生的煙氣可能將壁面熏黑，使輻射率發生改變。

在有限元熱分析中，處理兩壁之間的輻射傳熱時需要引入中間節點，以中間節點建立表面效應單元分別向兩壁進行輻射傳熱，表面輻射率由實際情況決定。殼體兩壁與空氣夾層之間的對流屬于自然對流，常壓下自然對流準則方程為[9]：

Nu=CRan

(3)

式中：Nu為努賽爾數；Ra為瑞利數，是格拉曉夫數和普朗特數的乘積(Ra=Gr·Pr)；C為系數，取決于加熱狀態；n為指數，取決于流動狀態。

為了便于計算，將式(3)中所涉及的物性參數歸結到一起，得到的對流換熱系數hf可以簡化為：

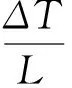
(4)

式中：A取決于壁面幾何形狀、邊界條件和流動狀態的參數，本研究取A=1.32，n=1/4；ΔT為兩壁面溫差；L為定型尺寸，本研究涉及的模型可按式(5)修正其定型尺寸[10]：

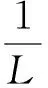
(5)

式中：L水平為結構水平尺寸，m；L豎直為結構豎直尺寸，m。

按照式(4)和(5)分別計算了當溫差為0～300K時的對流換熱系數，取其算術平均值hf=5.15W/(m2·K1)為本研究空氣夾層的對流換熱系數。

2.3 炸藥受熱分解放熱模型

炸藥的熱分解是一個自加速過程，隨著系統熱量的不斷積累，炸藥溫度急劇上升，直至點火。表征炸藥這一特征行為的熱傳導方程如下[11]：

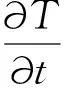
(6)

式中：ρ為炸藥密度，kg/m3；C為炸藥比熱容，J/(kg·K)；T為炸藥溫度，K；λ為導熱系數，W/(m·K)。S為源項，J/(m3·s)，即炸藥熱分解放出的熱量，可采用Arrhenius零級反應表示[12]：

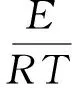
(7)

式中：Q為分解反應熱，J/kg；Z為指前因子，s-1；E為活化能，J/mol；R為普適氣體常數。

為比較不同炸藥在加熱過程中的熱響應，本研究選取HMX、RDX和TATB 3種炸藥進行計算，由于不同的測試方法測得的炸藥熱爆炸參數不同，研究中選取了同一種測試方法得到的熱物性參數，相關參數見表1[13]。在有限元計算中，隨溫度變化的放熱量(即源項S)作為初始條件加入控制方程。

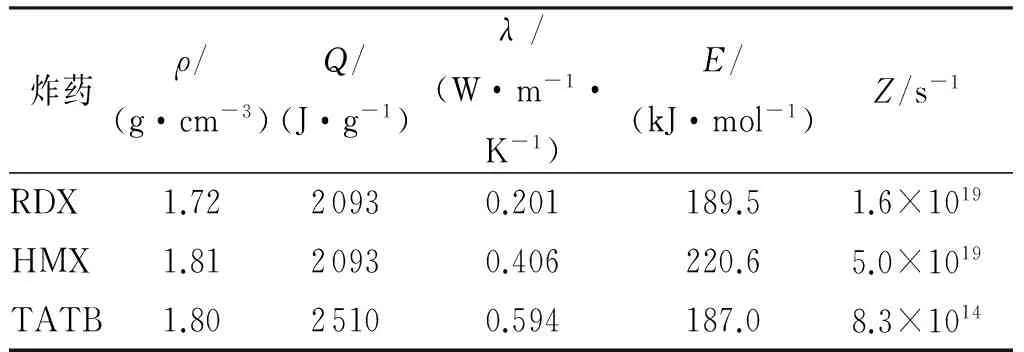
表1 3種炸藥的熱物性參數

3 數值模型及計算結果分析

3.1 計算模型及特征點的選取

利用有限元計算方法對圖2及圖3所示的模型在不同溫度下的傳熱模型進行數值建模，計算并分析了一維熱爆炸炸藥試樣在不同因素影響下，內部炸藥樣品溫度響應和熱點火延滯時間。為方便比較不同因素影響下的計算結果，取圖4所示的內部炸藥的幾個特征點進行討論。特征點1、2、3分別位于藥柱1/2高度的內部、中間和邊緣。

3.2 加熱方法的影響分析

炸藥為RDX，在473K分別對油浴加熱及空氣浴加熱進行數值計算，得到了炸藥熱點火延滯時間、熱點火時炸藥的溫度響應及點火點和特征點溫升時間歷程(空氣浴加熱時取其系統輻射率為0.2)。計算結果表明，油浴加熱時RDX在151.7s時發生熱點火，而空氣浴加熱時，RDX在3372.6s時發生熱點火。熱點火時RDX的溫度分布云圖見圖5。

由圖5可知，油浴加熱和空氣浴加熱下發生熱點火的位置分別位于藥柱兩端和中心位置處，熱點火的位置不同，溫度分布方式也不同。這是由兩種不同的熱傳遞方式導致的：油浴加熱時試件直接與恒溫的加熱介質接觸，相當于第一類熱邊界條件(恒溫表面)，熱量很快通過鋁合金套管傳入炸藥，且藥柱兩端同時接受兩個方向的熱量，因此熱量積累較快，炸藥熱分解釋放的熱量不能及時散發，因此該位置附近發生熱點火；空氣浴加熱時由于非接觸方式加熱，主要靠輻射及對流，溫升較慢，因此在RDX開始大量熱分解前，其在整個加熱過程中基本處于溫度平衡狀態，且由于樣品尺寸較小，幾乎沒有溫差。當樣品溫度達到熱分解溫度后，樣品分解產生的熱量大于接受的熱量，溫度開始上升，金屬套管的導熱系數遠遠大于樣品的導熱系數，靠近金屬套管的炸藥散熱比內部炸藥快，內部炸藥熱量積累較快，因此空氣浴加熱時，樣品發生熱點火的位置為試樣中心處。

圖6為兩種不同加熱方式下點火點的溫升-時間歷程。由圖6可知，油浴加熱時，熱點火前點火點的平均溫升速率高達88K/min，而空氣浴加熱發生熱點火前溫升速率僅為4.7K/min。

圖7為兩種加熱方式特征點的溫升-時間歷程。由圖7可看出，油浴加熱時特征點3由于離鋁合金套管近，溫度迅速升至473K(跟油浴溫度一致)，而特征點1、2由于炸藥樣品導熱系數較低且外界直接處于473K的恒溫環境，溫升較慢、溫度梯度較大。空氣浴加熱時，受加熱方式影響，熱量傳入炸藥樣品較慢，因此特征點1、2、3在發生熱點火前溫度基本一致，溫升曲線幾乎重合。

炸藥樣品在一定溫度下的一維熱爆炸試驗裝置中發生反應時間的長短是判斷該炸藥是否是鈍感炸藥的重要判據。為比較3種典型炸藥主要成分在不同加熱方式和溫度環境下的熱點火延滯時間，對相應的工況進行了計算，計算結果見表2。

由表2可知，隨著溫度的升高，熱點火延滯時間減小；同一溫度下，RDX熱點火延滯時間最短，HMX次之，TATB最長。TATB在環境溫度高于553K時才會發生熱點火反應。

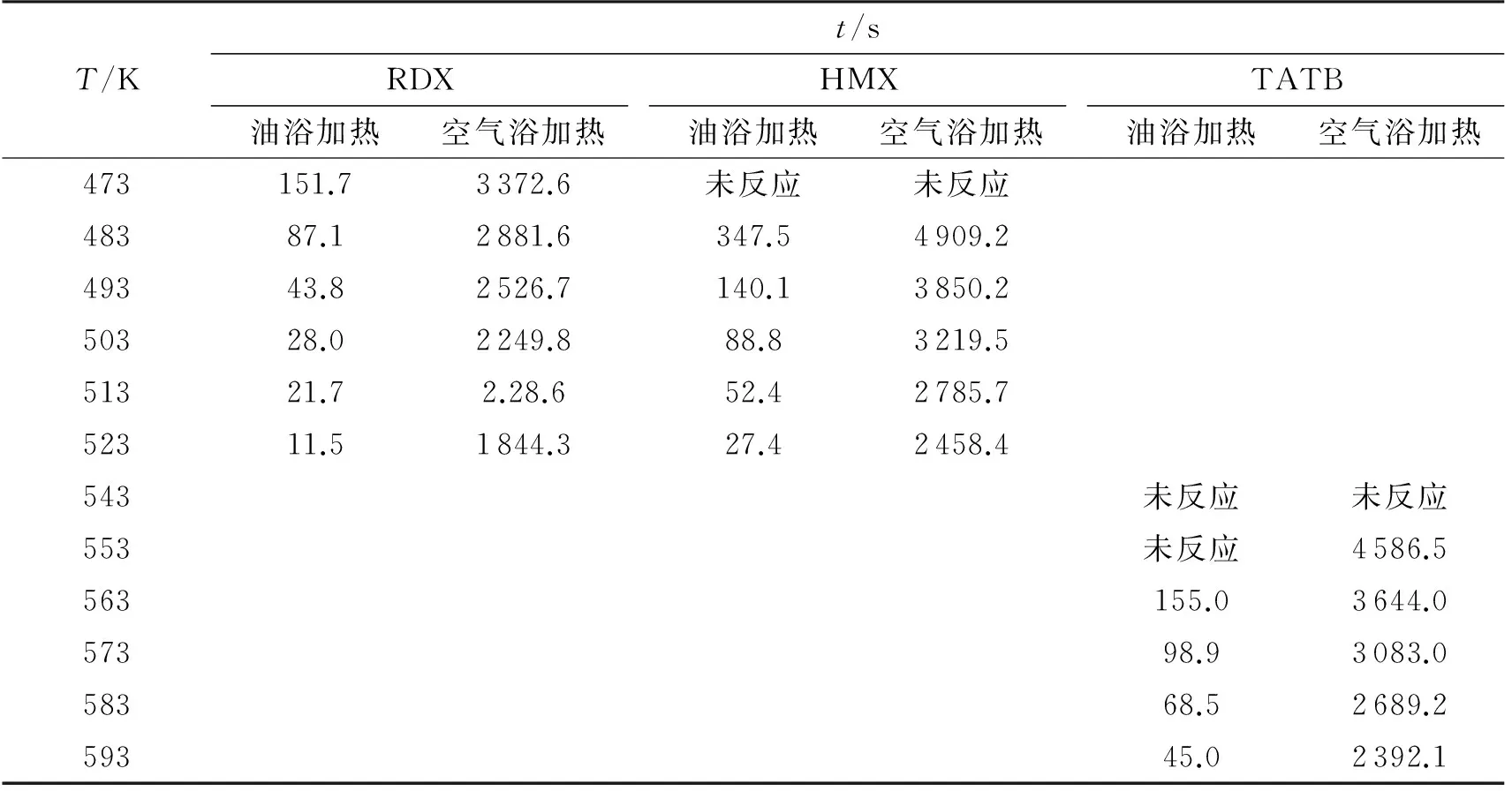
表2 3種炸藥在不同溫度和加熱方式下的熱點火延滯時間

3.3 輻射率影響分析

為比較相同溫度下，不同輻射率對熱點火延滯時間的影響，分別計算了483K(TATB為鈍感炸藥，環境溫度為553K)空氣浴加熱時，不同輻射率下RDX、HMX和TATB的熱點火延滯時間，結果見表3。

由表3可知，對同一種炸藥在相同溫度下，隨系統輻射率的降低，其熱點火延滯時間增加。RDX、HMX和TATB炸藥輻射率由0.9降至0.1時，熱點火延滯時間分別增加了180.1%、168.9%和169.3%。通常一維熱爆炸試驗時，加熱裝置會重復使用，炸藥樣品為新加工件，其表面輻射率約在0.1～0.2之間，而重復使用的加熱裝置由于炸藥反應產生的煙氣會沉積在表面，使其表面輻射率發生變化，很難確保每次試驗時表面輻射率一致。因此，建議對試樣和加熱裝置表面進行發黑處理，保證每次試驗時輻射率基本一致。

表3 不同系統輻射率對炸藥熱點火延滯時間的影響

3.4 對流換熱系數影響分析

由于空氣浴加熱的起始溫度不同，溫差和重力驅動空氣造成的對流換熱系數亦不同。為比較相同溫度、相同系統輻射率(均為0.2)環境下，不同對流換熱系數對炸藥樣品熱點火延滯時間的影響，對不同工況進行了計算分析，結果見表4。

由表4可知，相同溫度、相同系統輻射率情況下，對流換熱系數越大，其熱點火延滯時間越小。進一步分析可知，對同一種炸藥在同一溫度下對流換熱系數由9W/(m2·K)降至1W/(m2·K)時，熱點火延滯時間分別增加了144.6%、120.7%和86.4%。表明溫度越高，空氣復合傳熱中輻射占的比例越大，對流換熱系數對內部炸藥熱點火延滯時間影響較小。

表4 不同對流換熱系數對炸藥熱點火延滯時間的影響

4 結 論

(1)建立了一維熱爆炸試驗裝置兩種加熱方式數值模型，計算分析了加熱方式(空氣浴、油浴)、空氣浴加熱時系統輻射率、對流換熱系數對炸藥樣品熱點火延滯時間的影響。結果表明，相同溫度下，油浴加熱發生熱點火的延滯時間遠小于空氣浴加熱。

(2)空氣浴加熱時，系統輻射率降低，內部炸藥熱點火延滯時間大幅增加；對流換熱系數增大，內部炸藥熱點火延滯時間大幅下降。

[1] 文雯，呂子劍.不同約束條件對ODTX試驗結果的影響，GF-A0163146G[R].2011.

WEN Wen，Lü Zi-jian. Influences of different confined condition on ODTX test, GF-A0163146G[R].2011.

[2] Henkin, H, McGill R. Theory of thermal explosion[J].. Industrial Engineering Chemistry, 1952, 44: 1391.

[3] 金韶華，松全才.炸藥材料[M].西安：西北工業大學出版社，2009.

[4] Rogers R N. Experiment studies of small-scale cook-off bomb[J] .Thermochemical Acta, 1970, 1:1-10.

[5] Slape R J. IHE material qualification tests description and criteria, MHSMP-84-22[R]. Amarillo: Mason and Hanger-silas. Mason Co., Inc, 1984.

[6] 文雯，向永，呂子劍.鈍感炸藥一維熱爆炸試驗研究[C]∥全國危險物質與安全應急技術研討會.綿陽：中國工程物理研究院，2011.

WEN Wen，XIANG Yong，LV Zi-jian. ODTX test research of insensitive explosive[C]∥Conference of China’s Hazard Material and Safe Emergency Technology.Mianyang: CAEP, 2011.

[7] 楊世銘，陶文銓.傳熱學[M].第四版.北京：高等教育出版社，2006：4-15.

[8] 羅群生，史光梅，李明海.有限元分析中空氣夾層傳熱處理方法及其驗證[J].包裝工程，2011，32(23)：117-122.

LUO Qun-sheng，SHI Guang-mei，LI Ming-hai. Air interlayer heat exchange treatment method using finite element and its validation[J].Packing Engineering，2011，32(23)：117-122.

[9] Incropera F P, DeWitt D P, Bergman T L, et al. Fundamentals of Heat and Mass Transfer[M]. Hoboken: John and Wiley & Sons，Inc，2007:349-350.

[10] 李明海.火災環境下抗事故包裝結構熱-力耦合響應的數值模擬GF-A-0090584[R].2008.

[11] 牛余雷，南海，馮曉軍，等.RDX基PBX裝藥烤燃試驗與數值計算[J].火炸藥學報，2011，34(1)：32-37.

NIU Yu-lei，NAN Hai，FENG Xiao-jun, et al. Cook-off test and its numerical calculation of RDX-based PBX explosive[J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao)，2011,34(1)：32-37.

[12] 陳朗，馬欣，黃毅民，等.炸藥多點測溫烤燃實驗和數值模擬[J].兵工學報，2011，32(10)：1230-1236.

CHEN Lang，MA Xin，HUANG Yi-min, et al. Multi-point temperature measuring cook-off test and numerical simulation of explosive[J].Acta Armamentarii，2011，32(10)：1230-1236.

[13] 楚士晉.炸藥熱分析[M].北京：科學出版社，1994：288.

NumericalSimulationofHeatTransferonOne-dimensionalTime-to-ExplosionTest

WU Song，CHEN Jun，LI Ming-hai

(Institute of System Engineering, CAEP, Mianyang Sichuan 621900,China)

Aiming at the main heat trasfer problems involved in the heating process, the complex heat transfer model of air layer and the thermal decomposition heat release numerical model of explosive were established, respectively. The effects of system emissivity and convective heat transfer coefficient of air on the thermal ignition delay time of RDX, HMX,HTPB explosive samples when heating by oil bath and air bath at 473K were calculated and analyzed. The results show that the ignition time of RDX by oil bath and air bath under the temperature of 473K are 151.7s and 3372.6s,respectively,showing that under the same temperature and explosive, the thermal ignition delay time under oil bath heating was far less than that under air bath heating. As air bath heating, the ignition delay time increases with the decrease of the emissivity under the same temperature and explosive . The ignition delay time of RDX, HMX and TATB increase by 180.1%,168.9% and 169.3% respectively when the emissivity decreases from 0.9 to 0.1. The thermal ignition delay time increases with the decreases of the convective heat transfer coefficient under the same temperature and the same emissivity.

one-dimensional time-to-explosion; air bath; oil bath; emissivity; thermal ignition delay time

TJ55;TB487

A

1007-7812(2017)05-0039-06

10.14077/j.issn.1007-7812.2017.05.007

2017-03-20；

2017-08-10

吳松(1986-)，男，碩士，從事武器熱安全和環境試驗技術研究。E-mail：wusong@zju.edu.cn