基于模態分離算法的管道焊縫缺陷模擬

,

(華東理工大學承壓系統與安全教育部重點實驗室,上海 200237)

基于模態分離算法的管道焊縫缺陷模擬

葉夢雅,胡明慧

(華東理工大學承壓系統與安全教育部重點實驗室,上海200237)

在溫度、壓力、介質腐蝕、振動等影響下,在役工業管道焊縫內部的小缺陷易發展成裂紋,對管道安全運行產生危害。在模態對稱分離算法檢測單焊縫管道缺陷的基礎上,基于L(0,2)模態導波進行數值模擬,分別以前焊縫缺陷對稱面、彎管對稱面為縱坐標建立新的笛卡爾直角坐標系,根據對稱原理,易于提取缺陷特征。模擬結果表明,非對稱幅值與裂紋深度呈指數函數關系,該方法可以實現雙焊縫和彎管焊縫缺陷的識別和定量。

超聲導波; 焊縫缺陷; 模態分離;L(0,2)模態; 模擬

管道在石油、化工和天然氣等領域應用廣泛,工業管道大多采用彎管與直管焊接而成,為保證管道的安全運行,需對其定期檢測。由于焊縫是焊接管道缺陷產生的高發部位,對管道焊縫區域缺陷檢測的研究具有很大的現實意義。

超聲導波具有傳播距離遠、檢測效率高等優點,被廣泛運用于管道缺陷檢測。由于導波的多模態和頻散特性,可根據導波在裂紋等缺陷處發生模態轉換及其反射波來判斷是否存在缺陷。由于焊縫的彈性模量、密度等參數與管道存在差異,因此對于含缺陷的焊縫而言,既有焊縫反射回波,又有缺陷反射回波,且兩者波包產生疊加,難以分離,使超聲導波應用于焊縫缺陷檢測變得困難。目前,使得用超聲導波進行焊縫缺陷的檢測大多集中在板焊縫的研究,例如Legendre等[1]用電磁超聲導波提出小波分析信號處理方法,對板焊縫進行了檢測。只有少數針對直管道單焊縫的研究成果。Nishino等[2]基于L(0,1)模態,對焊接管道進行了缺陷檢測,總結了回波信號與缺陷大小的關系,但他并未對焊縫處的缺陷進行檢測。劉秋閣[3]提出對稱與非對稱分離算法,實現了焊縫單缺陷的檢測及周向定位,但未實現在前焊縫有缺陷的情況下對后焊縫進行缺陷的檢測。Demma等[4]采用有限元分析了L(0,2)模態導波經過彎頭時的模態轉換情況,為本文彎管焊縫缺陷檢測的研究奠定了基礎。

在前人研究的基礎上,本文運用對稱與非對稱模態分離算法,基于L(0,2)模態導波進行數值模擬,分別以前焊縫缺陷對稱面、彎管對稱面為縱坐標建立新的笛卡爾直角坐標系,得到橫縱坐標方向上管道非對稱幅值曲線,實現了雙焊縫和彎管焊縫缺陷的識別和定量。

1 基本理論

1.1檢測原理

超聲導波在管道中的傳播方式如圖1所示。

圖1 超聲導波管道傳播原理圖Fig.1 Principle of ultrasonic guided wave propagation in pipes

超聲導波在傳播過程中,遇到不均勻材料介質會發生反射和頻散。當遇到對稱結構時,會產生對稱的反射波;當遇到非對稱結構時,會產生非對稱的反射波。所以,導波遇到無缺陷焊縫,其反射回波是對稱的,遇到含有缺陷的焊縫,其反射回波幅值將以缺陷為中心對稱分布,缺陷處的反射回波幅值最大,以此來檢測及定位焊縫缺陷。

1.2管道激勵模態選擇

根據彈性波動力學運動方程,管道的頻散方程[5]見式(1):

|Cij|=0

(1)

其中,Cij為固體媒介的彈性系數(i,j為1,2,…,6),與管道尺寸、材料、波數有關。

焊縫坡口形狀為V型,根據GB/T 31032—2014焊接標準,焊縫寬度為8 mm。超聲導波頻散現象表明焊縫寬度相對于管道長度影響較小,因此本文研究忽略了管道中焊縫對頻散特性的影響。

本文研究對象為碳質量分數小于0.3%,外徑100 mm,壁厚5 mm的碳鋼管道。現用于檢測管道缺陷的導波模態主要有縱波L(0,2)和扭轉波T(0,1)模態。相對T(0,1)模態,L(0,2)具有傳播速度快、易區分出缺陷波包、對管道周向、徑向缺陷敏感、對軸向缺陷不敏感的特點[6]。結合焊縫缺陷一般表現為裂紋和腐蝕、以及軸向尺寸小的特點,本文選擇L(0,2)模態導波對管道焊縫缺陷進行模擬。

2 焊縫缺陷數值模擬

2.1模型建立及網格劃分

本文采用商業化軟件ABAQUS對直管和彎管進行模擬。管道外徑100 mm,壁厚5 mm。不考慮焊縫余高的影響。管道、焊縫材料參數如表1所示。

表1 管道與焊縫材料參數

結合對稱與非對稱分離算法,傳感器數量大于該頻率存在的非對稱模態的最高階數[7]。在管道端部周向均勻分布36個(4的倍數)節點來激勵和接收。為對比不同截面缺損率對回波信號的影響,徑向分5等份。根據波傳動效應,一個波長方向至少20個單元[8],單元格周向長度a,有限元模擬時間步長h,總的計算時間H[9]應分別滿足:

(2)

(3)

(4)

式中:Cp為導波相速度;Cg為導波群速度;f為激勵頻率;l為管道的總長度。

2.2雙焊縫缺陷模擬

激勵頻率為70 kHz的L(0,2)模態導波分別對前后焊縫均無缺陷、前焊縫有缺陷后焊縫無缺陷、前焊縫有缺陷后焊縫有缺陷(前后焊縫缺陷對稱面位于同一平面內)、前焊縫有缺陷后焊縫有缺陷(前后焊縫缺陷對稱面位于不同平面內)的4種情況進行模擬分析。得到回波信號時程曲線如圖2(a)～2(d)所示。

當雙焊縫中均無缺陷時,從圖2(a)時程曲線中依次可得到激勵回波、兩個焊縫回波及端面回波。當前焊縫存在缺陷時,如圖2(b)所示,在兩個焊縫回波間出現新模態波。但當前后焊縫均存在缺陷時,如圖2(c)、2(d)所示,與圖2(b)差異不大,很難辨別后焊縫是否存在缺陷。對比圖2(a)～2(d)可以看出,利用L(0,2)模態導波可以有效識別前焊縫缺陷,但當前焊縫存在缺陷時,后焊縫的缺陷識別變得困難。

2.3彎管焊縫缺陷模擬

頻率為70 kHz的L(0,2)模態導波分別對無焊縫、無缺陷焊縫、缺陷在彎管焊縫內壁、側壁以及外壁的彎管進行了模擬,得到回波信號時程曲線如圖3、圖4所示。

圖3 彎管焊縫缺陷分布反射回波對比圖Fig.3 Reflected waveform comparison of defect weld in different area of an elbow

對比圖3(a)～3(c)可以發現,缺陷分布在彎頭外壁的焊縫反射波幅值明顯大于缺陷分布在彎頭其他位置的反射波幅值。這一現象符合導波穿過彎頭,能量由內側向外側轉移,在彎頭外側聚焦的規律。

從圖4(a)可以看出,彎管無焊縫模擬得到的時程曲線中,僅有由彎曲存在產生的新模態波包;圖4(b)表明當彎管存在焊縫時,會出現焊縫波包。對比圖4(b)和4(c)有缺陷和無缺陷的焊縫波形圖,難以辨別焊縫處是否存在缺陷。

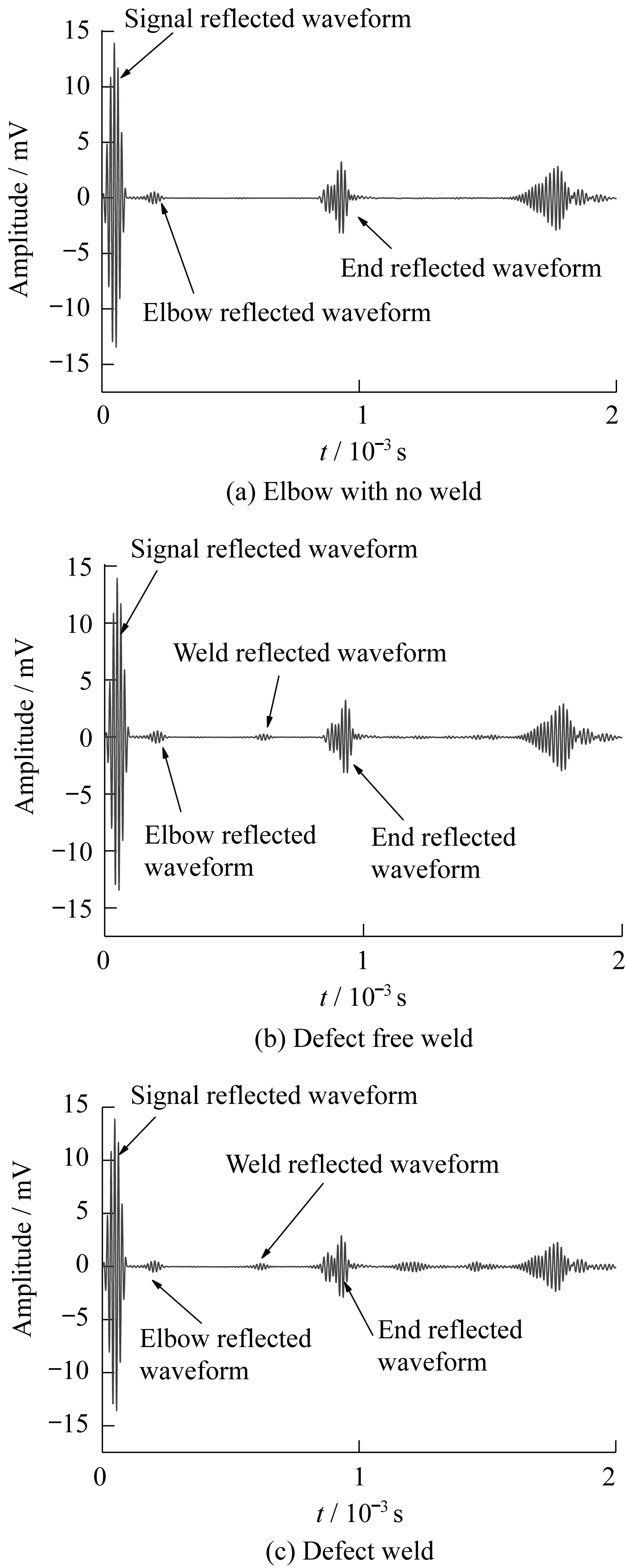
圖4 彎管焊縫有無缺陷反射回波對比圖

3 信號處理與結果分析

3.1對稱與非對稱模態分離

根據時程曲線圖判斷前焊縫反射回波波峰出現的時間,提取該時刻周向36個傳感器反射波幅值,繪制成如圖5所示雷達圖。

圖5 前焊縫周向節點反射波幅值圖Fig.5 Circumference amplitude value of the first weld

根據導波檢測原理及圖5中36個節點幅值分布可直接判斷前焊縫缺陷關于1、19節點所在直線對稱。基于文獻[3]使用的模態分離方法,沿周向均勻布置36個傳感器。分別以前焊縫缺陷對稱面、彎管對稱面為縱坐標建立新的笛卡爾坐標系,設計模態分離方法如下:

S=|S1+S2+…+S35+S36|

(5)

SH=|S2-S18|+|S3-S17|+…+|S9-S11|+

|S36-S20|+|S35-S21|+…+|S29-S27|

(6)

SV=|S2-S36|+|S3-S35|+…+|S18-S20|

(7)

其中:S為36個傳感器接收到數值之和的絕對值;SH、SV分別為新的笛卡爾坐標系下以橫坐標、縱坐標為對稱軸,傳感器數值之差的絕對值之和。SH、SV越大,表明非對稱程度越大。

3.2雙焊縫模態分離

在3.1節的理論基礎上,進行雙焊縫管道缺陷檢測,得到前后焊縫均無缺陷、前焊縫有缺陷后焊縫無缺陷、前焊縫有缺陷后焊縫有缺陷(前后焊縫缺陷對稱面位于同一平面內)、前焊縫有缺陷后焊縫有缺陷(前后焊縫缺陷對稱面位于不同平面內)4種情況的模態分離圖,如圖6(a)～6(d)所示。

從圖6(a)可以得到,當焊縫均不含缺陷時,SH、SV均為0。對比圖6(b)、圖6(c)可知,當前焊縫存在缺陷時,兩個焊縫波包中,SH仍為0,SV不為0。與后焊縫無缺陷相比,后焊縫存在缺陷時焊縫波包波峰處SV增大。由圖6(d)可得,當前后焊縫缺陷對稱面位于不同平面時,后焊縫波包處SH、SV均不為0。

圖6 雙焊縫非對稱模態分離圖Fig.6 Asymmetrical mode separation of double weld

3.3彎管焊縫模態分離

以彎管對稱面為縱坐標建立笛卡爾直角坐標系,對彎管無焊縫、彎管含無缺陷焊縫、彎管含內壁缺陷焊縫、彎管含側壁缺陷焊縫以及彎管含外壁缺陷焊縫5種情況將彎管反射回波進行非對稱模態分離,如圖7所示。

從圖7(a)、7(b)可以看出,彎管無焊縫和存在無缺陷焊縫時,在彎頭和焊縫回波波包中,SH均為0,SV不為0。對比圖7(c)～7(e)可得,當焊縫缺陷位于彎頭內壁和外壁時,焊縫回波波包處SH仍為0,焊縫回波波包波峰處SV與圖7(b)相比明顯增大。當焊縫缺陷位于彎管側壁時,如圖7(d)所示,焊縫回波波包處SH和SV均不為0。

3.4焊縫缺陷定量

圖8為焊縫內部缺陷截面示意圖。圖8中,R為管道外徑,r為管道內徑,α為缺陷沿圓周管道分布的弧度值,b為管道截面中心到缺陷壁面的距離,r≤b≤R。本文中,R=50 mm,r=45 mm。

因此,完整的圓環截面積A和內部缺陷的截面積Ain分別為

A=π(R2-r2)

(8)

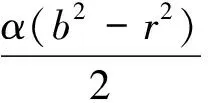
(9)

內部缺陷截面缺陷缺損率為

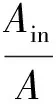
(10)

預制缺陷沿圓周管道分布的弧度α為π/9。分別取b為45、46、47、48、49 mm,根據公式(10)計算出相應的截面缺損率,提取焊縫回波波包與彎頭回波波包波峰處的SH、SV,繪制彎管焊縫SH幅值隨截面缺損率變化趨勢圖(圖9)及焊縫回波波包與彎頭回波波包波峰處SV之比隨截面缺損率變化趨勢圖(圖10)。

圖7 彎管焊縫非對稱模態分離圖Fig.7 Asymmetrical mode separation of weld elbow

圖8 焊縫缺陷示意圖Fig.8 Schematic diagram of weld defect

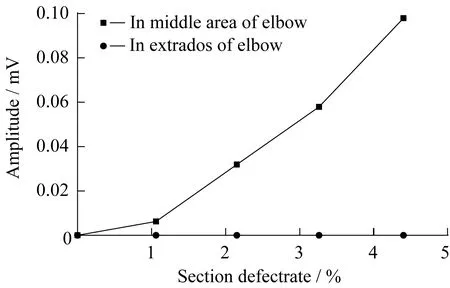
圖9 彎管焊縫SH幅值隨截面缺損率變化趨勢圖Fig.9 Variation trend of SH amplitude with section defect rate in bend weld

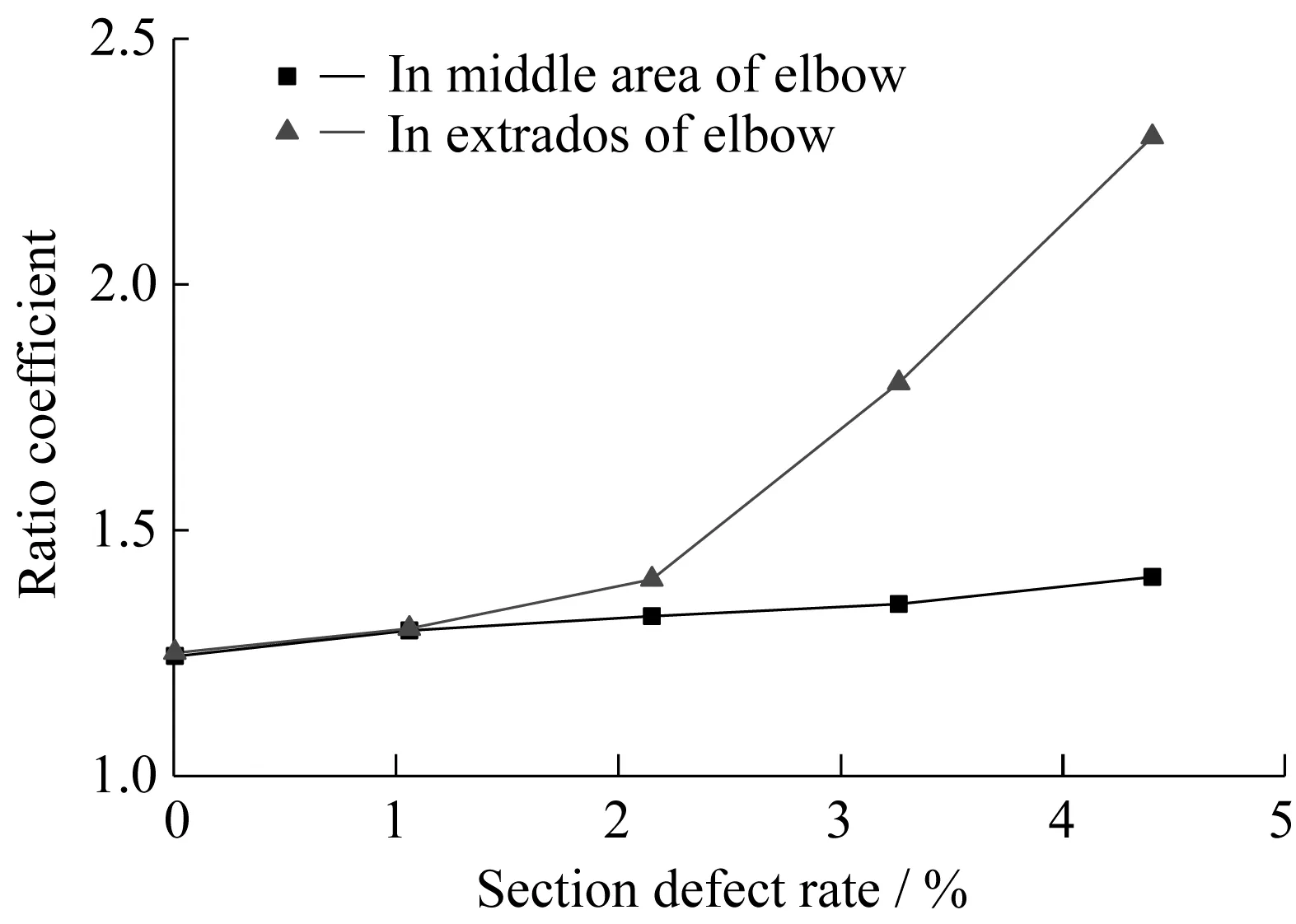
圖10 彎管焊縫SV之比隨截面缺損率變化趨勢圖Fig.10 Variation trend of ratio coefficient with section defect rate in bend weld

圖9表明,當焊縫缺陷對稱面與彎管對稱面在同一平面時,SH為0。當焊縫缺陷對稱面與彎管對稱面不在同一平面時,SH大于0,且隨截面缺損率增大而增大。圖10表明,當焊縫回波波包與彎頭回波波包波峰處SV之比大于1.24即可大致判斷彎管焊縫存在缺陷。以彎管外壁缺陷為例,得到焊縫回波波包與彎頭回波波包波峰處SV之比關于截面缺損率的擬合函數,實現缺陷定量,見式(11):

y=0.136 05ex/2.016 46+1.073 64

(11)

4 結 論

本文在模態對稱分離算法檢測單焊縫管道缺陷的基礎上,分別以前焊縫缺陷對稱面、彎管對稱面為縱坐標建立新的笛卡爾坐標系,利用ABAQUS軟件,基于L(0,2)模態導波進行數值模擬,給出了雙焊縫缺陷及彎管焊縫缺陷識別的定量方法。主要得出了以下結論:

(1) 模擬空管雙焊縫缺陷識別時,當時程曲線圖出現新模態波包時可判斷前焊縫存在缺陷。根據前焊縫周向節點反射波幅值分布雷達圖,可確定前焊縫缺陷對稱面。

(2) 模擬管道雙焊縫缺陷和彎管焊縫缺陷識別時,僅根據時程曲線圖難以判斷焊縫處是否存在缺陷。進行模態非對稱分離后,當后焊縫、彎管焊縫回波波包處SH大于0時即可判定焊縫處存在缺陷;當SH為0時,需根據焊縫回波波包與彎頭回波(前焊縫回波)波包波峰處SV之比判斷。當焊縫回波波包與彎頭回波波包波峰處SV之比大于1.24時,可確定彎管焊縫處存在缺陷。

[1] LEGENDRE S,MASSICOTTE D,GOYETTE J.Neural classification of Lamb wave ultrasonic weld testing signals using wavelet coefficients [J].Instrumentation and Measurement,2001,50(3):672-678.

[2] NISHINO H,MASUDA S,MIZOBUCHI Y,etal.Long-range testing of weld elbow pipe using theT(0,1) mode ultrasonic guided wave [J].Japanese Journal of Applied Physics,2010 ,49(11):1166021-1166026.

[3] 劉秋閣.基于超聲導波的管道焊縫區缺陷檢測研究[D].江蘇:江蘇大學,2016.

[4] DEMMA A,CAWLEY P,LOWE M,etal.The effect of bends on the propagation of guided waves in pipes [J].Journal of Pressure Vessel Technology,2005,127:328-335.

[5] 譚冰心,戴波.管道腐蝕缺陷超聲導波檢測數值模擬 [J].控制工程,2015,22(2):335-341.

[6] ALLEYNE D N,LOWE M J S,CAWLEY P.The reflection of guided waves from circumferential notches in pipes [J].Journal of Applied Mechanics,1998,65(9):635-641.

[7] 程載斌,王志華,張立軍,等.管道超聲縱向導波裂紋檢測數值模擬[J].應用力學學報,2004,21(4):76-79.

[8] SAEED Moaveni.有限元分析:ANSYS理論與應用[M].北京:電子工業出版社,2009:493-499.

[9] FRIEDRICH M,LAURENCE J,QU Jianmin.Modeling elastic wave propagation in waveguides with the finite element method[J].NDT and E International,1998,32:225-234.

SimulationforWeldDefectsinPipeBasedonModalSeparationAlgorithm

YEMeng-ya,HUMing-hui

(KeyLaboratoryofPressurizedSystemandSafety,MinistryofEducation,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

With the influence of temperature,pressure,medium corrosion and vibration,small defects in the weld can be grown into cracks,which will do harm to the in-service industrial pipelines.Based on the modal symmetry algorithm of defect detection of single weld pipeline,the simulation of modal guided waves inL(0,2) is carried out.According to the symmetry principle,it’s easy to extract the defect features.A new Cartesian coordinate is established by using the symmetry surface of the weld defects and weld elbow as the vertical axis respectively.The simulation results show that the asymmetric amplitude is in exponential function with the crack depth,and the method can realize the identification and quantification of defects in double welds and elbows.

ultrasonic guided wave; weld defect; mode separation; longitudinal modeL(0,2); simulation

TB559

A

1006-3080(2017)05-0717-07

10.14135/j.cnki.1006-3080.2017.05.018

2017-04-24

國家自然科學基金(51205133)

葉夢雅(1991-),女,浙江麗水人,碩士生,研究方向為管道焊縫缺陷導波檢測。E-mail:ymyeah122@163.com

胡明慧,E-mail:agile_hu@ecust.edu.cn