一種非線性PD控制曲面的簡易構造方法①

任永平 任守福 董富治

(太原衛星發射中心)

一種非線性PD控制曲面的簡易構造方法①

任永平 任守福 董富治

(太原衛星發射中心)

在簡要分析模糊控制原理的基礎上，提出了一種非線性PD控制曲面的簡易構造方法。首先在相平面上構建一對或兩對原點對稱的規則點，這些規則點對系統的控制作用可以通過簡單的凸組合和疊加計算得到。進一步對規則點的參數和控制曲面特征量之間的關系進行分析，得到控制參數調試準則。仿真結果表明：該方法可以對不同控制性能進行折衷。

非線性PD控制 控制曲面 模糊控制

在工程控制領域，對非線性PD控制器進行研究是有積極意義的。一方面，PD控制器本身在實踐中有許多應用[1,2]，另一方面，非線性PD控制器是非線性PID控制器的設計基礎，而后者是工程中最常用到的控制器。非線性PD控制器的設計方法有模糊控制、神經網絡控制等，這些方法的理論基礎較為完善，具備構造任意復雜曲面的能力[3,4]，但工程實現起來較為復雜。為了簡化問題，許多文獻采用非線性函數直接修正線性控制系數[5～7]，使控制器的性能隨系統誤差狀態而變化，這種方法簡單、高效，但缺點是曲面構造能力有限。

筆者提出一種非線性PD控制器的簡易構造方法——在分析模糊控制方法的基礎上，采用少量規則點和凸組合技術構造簡易的PD控制曲面。

1 非線性PD控制器的簡易構造和參數分析

1.1 構造方法

其中，u為規則輸出，i為規則數。

圖1 模糊控制器的控制曲面構造原理

用這個算式逐點計算相平面上的點就可以得到模糊控制曲面。

文獻[8]指出：如果規則數足夠多的話，模糊控制器可以逼近任意復雜的控制曲面。模糊控制器的這一特點在實際工程中意義不大，一方面，實際被控對象往往具有積分或慣性特性，控制曲面的小變化都會被系統濾掉，沒有必要把控制曲面構造得很精細；另一方面，規則數一多，調試工作量會增加。因此在實際工程中，往往只需要少量的幾個規則點，構建一個大體具有某一形狀的控制曲面就可以達到控制目標。

(1)

圖2 簡易控制曲面在相平面上的構造原理

規則點A-A′對狀態點E的影響關系定義如下：

(2)

其中,λ1是指A點對狀態點E的影響程度，λ2是指A′點對狀態點E的影響程度，設計參數mA為一大于零的常數。顯然，式(2)符合模糊控制中的距離越遠影響程度越小的原則。

狀態點E處的輸出通過如下凸組合得到：

由式(3)可以得到規則點A-A′的PD控制曲面，其零點線如圖2中的LA。

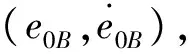
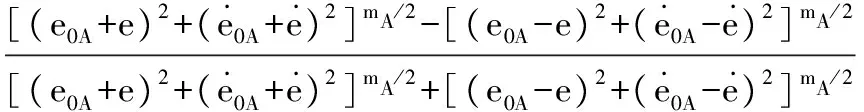
(4)

1.2 參數分析

圖1中的零點線L和e軸的夾角實際上反映了PD控制器零點的大小：kds+kp=kd(s+kp/kd)，L斜率越大，kp/kd越大，微分作用相對減弱，因此，零點線L可以用來刻畫控制曲面的特征。另外，圖1中的過零傾角θ能夠反映控制器的穩態剛度大小，它也可以作為一個特征量來刻畫控制曲面的大體特征。

從控制器參數設計角度看，有必要對零點線L、過零傾角θ和控制性能的關系，以及零點線L、過零傾角θ和式(4)中的設計參數的關系進行分析。

零點線L、過零傾角θ與控制性能的關系。前文介紹了過零傾角θ、零點線L和設計參數的關系，下面就這兩個控制曲面特征量和控制器性能的關系進行簡要的說明。一般地，過零傾角θ反映了控制器的剛度大小，在保證系統穩定性的基礎上，過零傾角θ越大，則系統抑制噪聲能力越強；而過零傾角θ越大，越容易使系統發生極限環振蕩，因此，對于時滯系統、大慣性系統等穩定性要求較為苛刻的系統，過零傾角θ不宜過大。

圖3 過零傾角θ與參數mA的關系

零點線L與規則點A-A′、B-B′和mA、mB的關系。規則點A-A′的零點線如圖4中的直線LA，同樣B-B′所形成的零點線為直線LB。根據正負取值關系，兩對規則點A-A′、B-B′按式(4)疊加形成的零點線LAB應介于LA和LB之間，因此可以通過調整規則點A-A′、B-B′的位置來調整LAB在相平面上的位置，但這種做法一方面調整能力有限，另一方面規則點的位置一般要大于系統誤差及其速度的最大值，因此它的位置一般不宜做調整。

筆者介紹一種變mA、mB參數的方法來調整零點線的方法，它可以按照誤差狀態e來選擇零點線的形狀，比如當誤差e較大時，希望LAB靠近LA；而當誤差e變小時，希望LAB靠近LB，因此，只需將mA、mB改變成如下函數即可：

(5)

其中emax、emin為系統最大誤差和最小誤差的估值(通常emin=0)，對應的參數mB的取值為mB_min、mB_max。式(5)的作用是：當誤差e大時，mB→mB_min、mA→mB_max，此時A-A′起主導作用，LAB靠近LA；當誤差e小時，LAB則要靠近LB。需要指出的是，這里的參數mA、mB的變化會影響過零傾角θ的調整，為此，可以考慮在式(5)計算結果的基礎上再疊加一個常數項以提高過零傾角θ，或是乘以一個小于1的系數以減小過零傾角θ。

圖4 零點線與規則點位置和參數mA、mB的關系

2 仿真示例

考慮被控對象G(s)=1/s(s+1)(s+2)，相應的線性控制PD控制參數為：kp=5.5、kd=4。為了檢驗控制性能，采用了如圖5所示的仿真結構。

圖5 示例仿真結構框圖

圖5中的白噪聲環節和延時環節用來測試控制系統的噪聲抑制能力和延時承受能力(即加大延時參數使系統產生等幅振蕩，它反映了系統的穩定裕度)，控制器分別采用線性PD控制器和下述兩種形式非線性PD控制器。

表1 采用一對規則點的非線性PD控制器與線性控制器的性能比較

由仿真可知，3種控制器的階躍響應輸出基本上是重疊的，即三者的時間性能相同，并且零點線也相同，進一步測試系統的延時承受能力和噪聲抑制能力也具有相同的性能，這表明：采用一對規則點所構造的PD控制器完全能夠實現線性PD控制器的功能。這種控制器折衷能力有限，若階躍響應時間性能確定，延時承受能力和噪聲抑制能力也就隨之確定。

為了更好地折衷性能指標，引入變mA、mB參數機制，考慮式(5)為如下函數：

(6)

這里，將式(5)中的mB_min取為0.5是為了防止系統在穩態時出現零極點對消，使系統退變為有差系統。選擇不同坐標點和控制參數，分別針對噪聲抑制和延時承受能力進行測試，測試結果見表2。

表2 采用兩對規則點的非線性PD控制器的性能測試結果

表2中，根據坐標點處的輸出值U0A、U0B值的不同，控制參數mA、mB的值也做相應的調整以構造不同特性的控制率。由測試結果可以看出，在階躍響應時間性能相同的情況下，通過參數mA、mB的調整，可以對噪聲抑制和延時承受能力進行折衷，這在線性和一對規則點的情況下是很難做到的。另外，非線性PD控制在強調某一性能時，必然會降低互為競爭的另一項指標，如表2中的噪聲抑制能力和延時承受能力，當控制器階次一定時，這一矛盾總是存在的。

3 結束語

在分析模糊控制原理的基礎上，提出一種簡易控制曲面構造方法。它和模糊控制的不同之處在于，筆者所提方法只采用少量的幾個規則點，并且它在相平面上的位置是任意的。另外，方法中和模糊控制的隸屬函數概念相對應的“影響程度函數”采用了距離的指數函數來表示。隨著這個指數的取值不同，控制器的性能將產生明顯的變化。由此，結合規則點位置坐標、輸出等參數的不同取值，設計出性能各異的非線性PD控制器。

筆者所提方法物理意義十分直觀，這也使得它的參數調試較為簡單，這一點在仿真示例中得到充分體現。另外，對于不同的控制指標的折衷問題，筆者所提方法只需要對一個指數參數進行調整，處理起來較為簡單。

[1] 李艷輝, 張暢, 周秀杰.一種新的FH迭代學習控制器設計[J].化工自動化及儀表, 2014,41(7):754～757.

[2] 曹敏, 徐凌樺, 何志琴.單神經元PID倒立擺系統及其仿真研究[J].化工自動化及儀表,2010, 37(1):28～29.

[3] 劉福才, 陳超.典型非線性模型的模糊辨識逼近精度分析[J].模糊系統與數學,2008, 22(6):104～113.

[4] 孫靈芳,董學曼,姜其鋒.模糊控制的現狀與工程應用關鍵問題研究[J].化工自動化及儀表,2016, 43(1):1～5.

[5] 蘇玉鑫,段寶巖.一種新型非線性PID控制器[J].控制與決策,2003,18(1):126～128.

[6] 韓京清.從PID技術到“自抗擾控制”技術[J].控制工程,2002,9(3):13～18.

[7] 魯照權,程健.步進式加熱爐鋼坯運動的非線性PID控制[J].化工自動化及儀表, 2016, 43(9):897～900.

[8] 張乃堯.典型模糊控制器的結構分析[J].模糊系統與數學, 1997,11(2):10～21.

ASimpleConstructMethodforNonlinearPDControlSurface

REN Yong-ping, REN Shou-fu, Dong Fu-zhi

(TaiyuanSatelliteLaunchCenter)

Based on briefly analyzing the theory of the fuzzy control, a simple method to construct control surface of nonlinear PD controller was proposed, in which, having one or two couple of rule points constructed in phase plane which are symmetric to the origin, and the control action of those rule points can be calculated by the mean of convex combination and superposition. Through further analyzing the relationship between the parameters of those rule points and the characteristics of control surface, the rules of parameter testing were obtained. Simulation results indicate that, this method can compromise the performance confliction.

nonlinear PD control, control surface, fuzzy control

任永平(1966-)，高級工程師，從事自動控制、檢測技術的研究， waterman4633@sina.com。

TP14

A

1000-3932(2017)03-0223-05

2016-08-14，

2017-01-11)