基于多元線性回歸與滾動窗的NOx排放量軟測量①

薛美盛 冀若陽 王 旭

(中國科學技術大學信息科學技術學院)

基于多元線性回歸與滾動窗的NOx排放量軟測量①

薛美盛 冀若陽 王 旭

(中國科學技術大學信息科學技術學院)

提出一種基于多元線性回歸與滾動窗的NOx動態軟測量建模方法，并研究模型更新周期和不同變量選擇方法對軟測量模型預測結果的影響。仿真結果表明：基于BIC向后剔除多元回歸和滾動窗方法的軟測量模型在運行較長時間后，仍然能夠較好地預測NOx的排放量。

NOx排放量 循環流化床鍋爐 動態軟測量 多元線性回歸 滾動窗

過程工業中常存在一些對系統控制品質有重要影響但又難以直接測量的變量[1]，如組分、沸點、閃點及粘度等，軟測量技術是獲取這些變量的重要手段。此外，盡管有些變量可以直接用硬件儀表測量，但時間成本或經濟成本很高，而且有維護耗時、需要標定、老化、測量噪聲大及精度不夠等問題[2]。軟測量技術既可以作為備件與現有的測量裝置并列運行，減少測量滯后和噪聲影響，也可以替代昂貴的儀表，降低測量成本[3]。

軟測量建模方法有機理建模、數據驅動建模和混合建模3種[4]。目前，大部分軟測量研究針對的是靜態軟測量模型。為了進一步提高軟測量模型的精度和魯棒性，動態軟測量模型成為今后的研究方向之一[5]。回歸分析是一種經典的軟測量建模方法，有學者將多元線性回歸方法用于循環流化床鍋爐NOx軟測量建模，取得了較好的預測效果[6]。但靜態模型不考慮對象的動態特性，在系統工作點遷移時，估計結果不夠準確。滾動窗方法通過不斷更新建模區間內的數據，使模型能夠始終反映系統的當前狀況，可以提高軟測量模型的準確程度[7]。

筆者基于多元回歸方法和滾動窗方法，提出一種動態軟測量建模方法，將它運用到循環流化床鍋爐脫硝系統NOx排放量的軟測量中，并研究模型更新周期與不同變量選擇方法對NOx排放量軟測量模型預測性能的影響。

1 回歸變量的選擇

在多元回歸分析中，回歸變量的選擇對回歸方程的質量有重要影響。若遺漏了重要的回歸變量，回歸模型的效果不會好；若引入過多的回歸變量，則可能出現過擬合，影響模型的穩定性。

回歸變量的選擇方法主要有4種：最優子集法、向前選擇法、向后剔除法和逐步回歸法。最優子集法考慮輸入變量集合的所有子集，找出其中的最優子集作為模型輸入。對于含有p個候選輸入變量的模型，其輸入變量子集有2p個。隨著p的增大，逐個嘗試找出最優子集模型的計算代價指數上升。向后剔除方法從含有全部回歸變量的模型開始，逐步從模型中剔除回歸變量來計算最優子集。向前選擇法從不含回歸變量的模型開始，通過逐步向模型中加入回歸變量來求解最優子集。逐步回歸法結合了向前選擇和向后剔除，在逐步加入回歸變量的過程中進行各種檢驗，若沒有通過檢驗則采用向后剔除法，兩種方法交替進行直到找到所有的顯著變量，并且選擇的所有變量都是顯著的。

評估子集回歸模型的信息準則主要有F檢驗、均方誤差(MSE)、MallowsCP、調整R2、赤池信息準則(AIC)及貝葉斯信息準則(BIC)等[8]。其中，AIC和BIC是兩種最具代表性的信息準則[9]。

2 循環流化床鍋爐NOx排放量軟測量

2.1 模型輸入量集合

化石燃料燃燒生成的NOx分為3種：熱力型、燃料型和快速型。其中，熱力型NOx的生成對溫度有很大依賴；燃料型NOx是煤燃燒產生的NOx的主要來源；快速型NOx比其他兩種NOx要少得多[10]。

對應于電站鍋爐運行環境，NOx的生成與燃燒溫度、氧量、煤種氮元素含量、燃料比、過量空氣系數和煙氣停留時間有較大關系[6]。選擇性非催化還原(SNCR)系統的脫硝效率與反應溫度、停留時間和NH3/NOx物質的量之比有關[11，12]。

考慮到循環流化床鍋爐的測點，將氨水流量、一次風量、二次風量、給煤量、石灰石量、床溫、一次風風煤比、二次風風煤比、一/二次風比及Ca/S(石灰石量/給煤量)等加入軟測量模型輸入量集合。

2.2 輸入滯后步數

相關系數可以用于計算滯后時間[13]。以氨水流量為例，圖1為由2015-07-16一天數據計算的氨水流量-NOx相關系數與滯后步數的關系曲線。在滯后步數為31時，相關系數達到最小值，即此段數據的氨水流量滯后步數為31步。圖2為2015-06-28～08-13中47天的氨水流量滯后步數直方圖，多數日期的滯后步數在25～35步之間，這里取30步。其他變量滯后步數的計算與此類似，不再贅述。

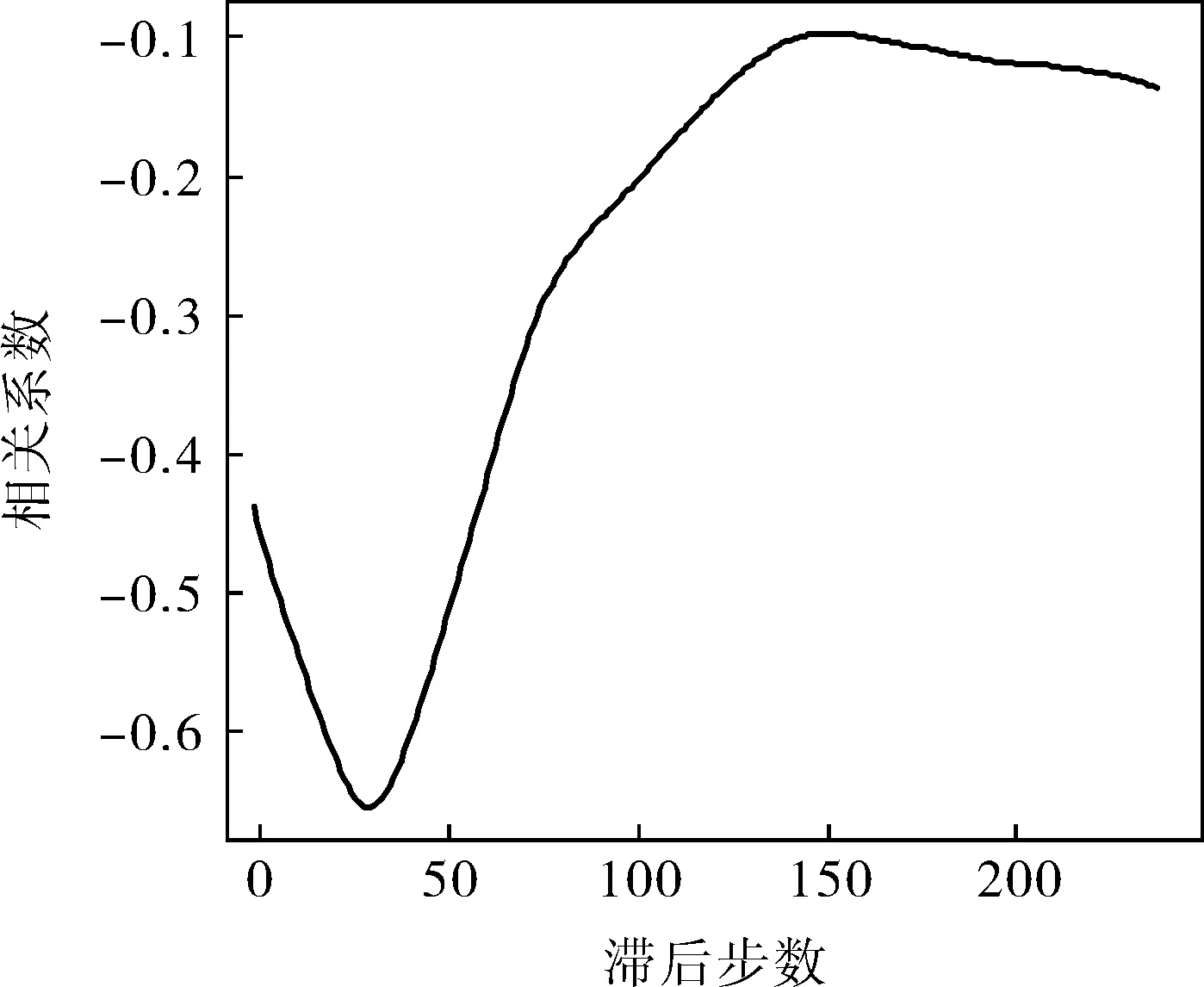
圖1 相關系數與滯后步數關系曲線

圖2 氨水流量滯后步數直方圖

2.3 基于滾動窗的多元回歸

實際系統工作時只與工作點附近的數據有較大相關性，而與遠離工作點附近的數據相關性不大[7]。工業過程由于進料、溫度及工藝等的變化，工作點往往會發生遷移。因此，采用固定數據得到的模型難以保證模型的準確性。滾動窗方法建立隨時間滾動的建模數據區間，在每個新的數據到來時都會更新模型，從而保證模型始終反映系統的當前狀況。但對于流程工業來說，過于頻繁地更新模型會給控制系統帶來較大的計算負擔。因此，在滾動窗方法中引入模型更新周期，模型只有在達到更新周期時才進行更新，這樣既能保證模型的準確性，又能降低控制系統的計算量。

記Ts為系統的采樣周期，Tu為模型更新周期，L為滾動窗窗口長度，并假定系統當前的建模信息可以從當前到過去L組數據中獲得。隨著系統運行，當達到模型更新周期時，最早的Tu/Ts條數據從建模區間滾動出去，新的數據加入建模區間，模型隨之更新。

基于滾動窗的多元回歸建模步驟如下：

a. 設置窗口長度L和模型更新周期Tu；

b. 數據預處理(缺失值處理、濾波和z-score標準化)；

c. 基于多元線性回歸方法建模；

d. 有新的測量數據時，利用新的測量數據進行預測；

e. 判斷是否達到模型更新周期，若沒有達到則返回步驟d，若達到則更新窗口樣本數據并返回步驟b。

2.4 模型預測結果

模型更新周期對預測性能有較大影響。考慮到NOx過程的慢時變特性和模型更新的計算量，較合理的模型更新周期為5～30min。選擇2015-07-31一天的數據，對模型更新周期對預測性能的影響進行研究。系統采樣時間為10s，滾動窗窗口長度為4 320，最大誤差和均方根誤差均為z-score標準化后的無量綱值。

圖3、4分別為基于AIC多元回歸預測的最大誤差、均方根誤差與模型更新周期的關系。向后剔除法的最大誤差和均方根誤差幾乎在所有的模型更新周期中都優于其他方法，向前選擇法和逐步回歸法的性能基本相當。

圖3 AIC預測結果最大誤差

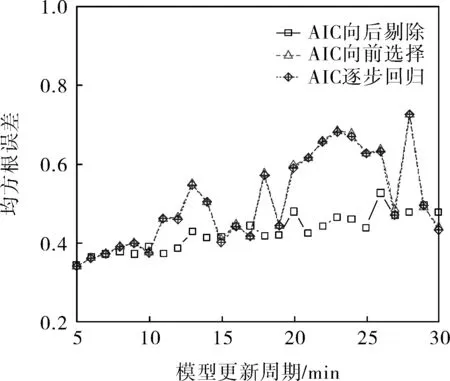
圖4 AIC預測結果均方根誤差

圖5、6分別為基于BIC多元回歸預測的最大誤差、均方根誤差與模型更新周期的關系。從最大誤差看，向后剔除法優于逐步回歸法，逐步回歸法優于向前選擇法。從均方根誤差看，沒有哪種方法表現出絕對的優勢。

將圖3與圖5，圖4與圖6進行對比后可以發現，隨著模型更新周期的增大，BIC回歸模型的最大誤差和均方根誤差的波動幅度要遠小于AIC回歸模型。

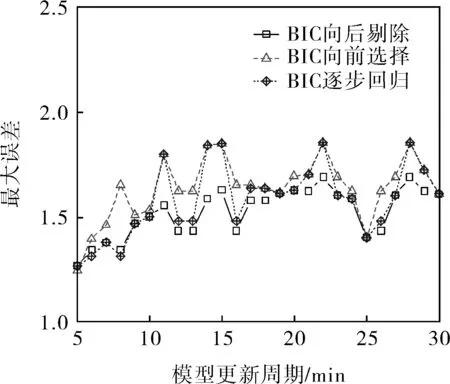
圖5 BIC預測結果最大誤差

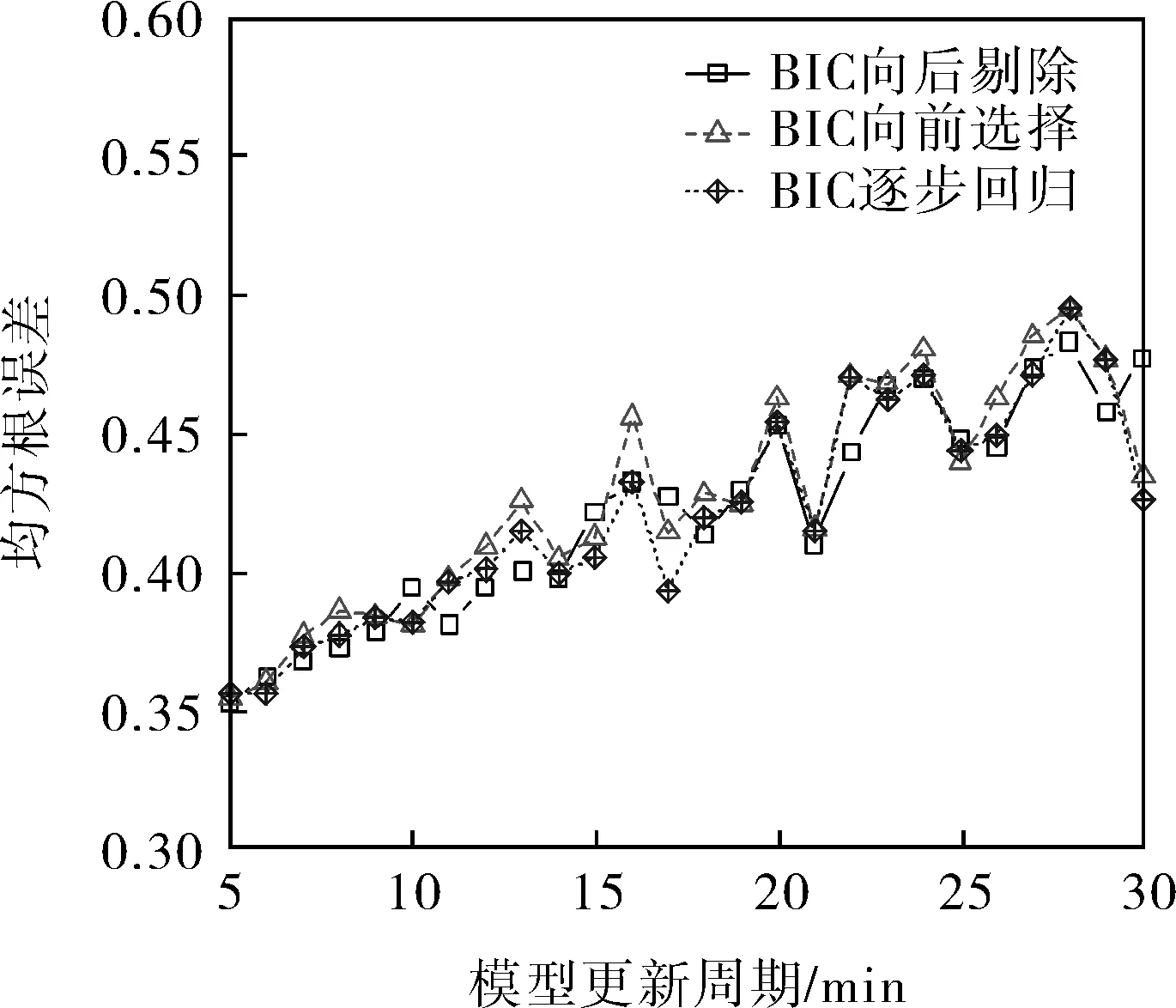
圖6 BIC預測結果均方根誤差

圖7給出了基于BIC向后剔除多元線性回歸模型的預測值與實際測量值曲線，模型更新周期5min。為了便于與測量值比較，將預測值逆標準化。其中，88.16%的預測值與實際測量值的偏差不超過2.50mg/m3，98.27%的預測值與實際測量值的偏差不超過5.00mg/m3，99.98%的預測值與實際測量值的偏差不超過10.00mg/m3，最大偏差11.78mg/m3。可見，即使在工況發生較大變化的情況下，軟測量模型依然有較好的預測效果。

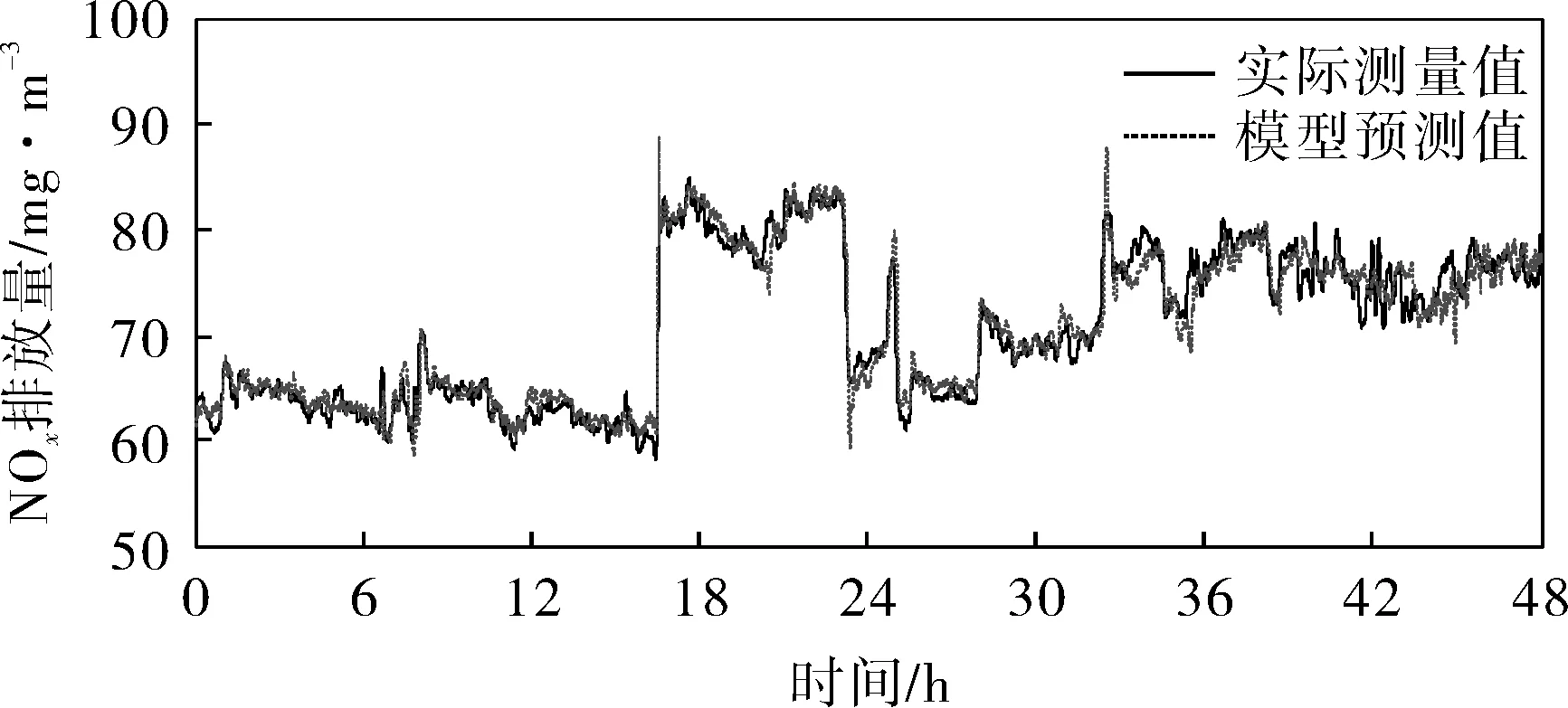
圖7 BIC向后剔除線性回歸模型預測結果

表1比較了靜態線性模型與更新周期為5min的滾動窗線性模型的預測結果。

表1 靜態線性模型與滾動窗線性模型預測結果

3 結束語

通過分析循環流化床鍋爐NOx生成和SNCR系統脫硝原理，建立合適的模型輸入量集合，利用多元線性回歸建立軟測量模型，并結合滾動窗使模型能夠跟蹤系統工況變化。在對比AIC、BIC兩種信息準則，向后剔除、向前選擇、逐步回歸法3種回歸量選擇方法后，建立基于BIC向后剔除法的NOx軟測量模型。該模型可以較好地適應工況變化，具有良好的魯棒性和預測性能。

[1] 馬勇,黃德先,金以慧.動態軟測量建模方法初探[J].化工學報,2005,56(8):1516～1519.

[2] Kano M,Fujiwara K.Virtual Sensing Technology in Process Industries:Trends and Challenges Revealed by Recent Industrial Applications[J].Journal of Chemical Engineering of Japan,2013,46(1):1～17.

[3] Liukkonen M,H?likk? E,Hiltunen T,et al.Dynamic Soft Sensors for NOxEmissions in a Circulating Fluidized Bed Boiler[J].Applied Energy,2012,97:483～490.

[4] 曹鵬飛,羅雄麟.化工過程軟測量建模方法研究進展[J].化工學報,2013,64(3):788～800.

[5] 俞金壽.軟測量技術及其應用[J].自動化儀表,2008,29(1):1～7.

[6] 白衛東,嚴建華,王飛,等.統計回歸方法在電站鍋爐氮氧化物排放量監測中的應用[J].動力工程,2004,24(3):431～435.

[7] 閻威武,常俊林,邵惠鶴.基于滾動時間窗的最小二乘支持向量機回歸估計方法及仿真[J].上海交通大學學報,2004,38(4):524～526.

[8] An H,Gu L.On the Selection of Regression Variables[J].Acta Mathematicae Applicatae Sinica,1985,2(1):27～36.

[9] Yang Y.Can the Strengths of AIC and BIC Be Shared[J].Biometrika,2005,92(4):937～950.

[10] 姜鵬志.循環流化床鍋爐低NOx排放特性及利用SNCR脫氮技術[J].中國電力,2010,19(6):6～10.

[11] 楊梅,張忠孝,于娟,等.循環流化床煙氣SNCR脫硝機理與實驗[J].燃燒科學與技術,2014,20(2):101～105.

[12] 何偉,魯明,李國強,等.SNCR脫硝系統的廣義預測控制[J].石油化工自動化,2016,52(1):38～41.

[13] 劉瑞蘭.軟測量技術若干問題的研究及工業應用[D].杭州:浙江大學,2004.

SoftSensorforNOxEmissionsBasedonMultipleLinearRegressionandSlidingWindow

XUE Mei-sheng, JI Ruo-yang, WANG Xu

(CollegeofInformationScienceTechnology,UniversityofScienceandTechnologyofChina)

A dynamic soft-sensing modeling method based on the multiple linear regression and the sliding window was proposed in this paper and the influence of model’s update period and different variable selection methods on the prediction results of the soft sensor model was studied. The results show that, the soft sensor model based on the sliding window and multiple linear regression which using backward elimination BIC selection method has good NOxemissions prediction performance even after running for a quite long time.

NOxemissions, circulating fluidized bed boiler,dynamic soft sensor, multiple linear regression, sliding window

TH83

A

1000-3932(2017)08-0721-04

2017-01-22，

2017-05-09)

薛美盛(1969-)，副教授，從事工業自動控制的研究。

聯系人冀若陽(1992-)，碩士研究生，從事先進控制與優化的研究，ryji@mail.ustc.edu.cn。