獨立分量分析與壓縮感知微地震弱信號提取方法

宋維琪 李艷清 劉 磊

(中國石油大學(華東)地球科學與技術學院，山東青島 266580)

獨立分量分析與壓縮感知微地震弱信號提取方法

宋維琪*李艷清 劉 磊

(中國石油大學(華東)地球科學與技術學院，山東青島 266580)

宋維琪，李艷清，劉磊.獨立分量分析與壓縮感知微地震弱信號提取方法.石油地球物理勘探，2017,52(5):984-989,1041.

結合獨立分量分析和壓縮感知理論各自的優勢，提出了獨立分量分析與壓縮感知聯合理論的微地震弱信號提取方法。從欠定盲信號分離和稀疏重構入手，通過對源信號的特征分析得到欠定盲分離模型中混合矩陣，基于該矩陣，建立欠定盲信號重構模型，采用壓縮感知理論的正交匹配追蹤方法和壓縮采樣匹配追蹤方法，對源信號進行重建。對混合矩陣、正交化、稀疏化及稀疏度等核心問題進行了系統分析，實現基于獨立分量分析與壓縮感知微地震弱信號重建方法。實際資料處理結果驗證了方法的可行性。

微地震資料 獨立分量分析 壓縮感知 稀疏重建 弱信號提取

1 引言

目前，對弱信號提取問題，大多是針對周期或準周期重復性信號開展的討論。微地震信號在時間采樣方向，具有局部脈沖的特點，大部分微地震信號的信噪比較低，特別是當有效信號較弱時，會完全被噪聲所淹沒，其信號提取就變得更為困難。前人在微地震弱信號檢測方面研究了多種方法，如盲源分離法[1]、隨機共振法、小波分析及自適應方法等，在微地震弱信號檢測方面取得了一定的效果。在微地震弱信號提取方面筆者也曾做過研究[2]，雖然取得了一些成果，但是面對復雜的微地震信號仍存在一定的不足。壓縮感知理論是近幾年興起的數據壓縮方法，對于提高資料的信噪比有一定的效果[3-5]，但是在微地震弱信號檢測方面，特別是被噪聲淹沒的弱信號的提取檢測問題，由于難以對弱信號進行稀疏化，應用效果不甚理想。

無論是盲分離技術還是壓縮感知技術，都牽涉到矩陣方程組的求解問題。迄今，對于超定和適定盲處理問題，已經提出了很多算法[6,7]，但是在實際應用中，傳統方法的結果一般很不理想，通常是通過獨立分量分析方法[8,9](ICA方法)實現求解。而很多信號在時間域上并不具有稀疏性，必須對其進行某種特殊的線性變換，使其在變換域中具有稀疏性[10-13]。

如何找到信號的最佳稀疏表示域是壓縮感知理論應用的基礎，只有選擇合適的稀疏基表示信號才能保證信號的稀疏度，從而保證信號的恢復精度[14-18]。在研究信號的稀疏表示時，可以通過稀疏度衡量信號稀疏表示能力。

壓縮感知對信號具有較強的稀疏化能力，但是在稀疏化過程中往往疏漏了一些弱信號的成分，而獨立分量分析能夠把各種信號相對較全面地揭示出來[19,20]，但是獨立分量存在過分稠密的問題，降低了對有效信號分析的能力，因此結合兩種理論的優勢，提出了基于獨立分量分析與稀疏重建微地震弱信號提取方法。

2 微地震盲信號壓縮感知重建

假設微地震信號有N個源信號s1，s2，…，sN，寫成矩陣形式S=[s1，s2，…，sN]T；M個觀測信號x1，x2，…，xM，寫成X=[x1，x2，…，xM]T。源信號和觀測信號之間的關系可以通過一個線性算子A表示為

X=AS=A[s1，s2，…，sN]T

(1)

即

(2)

N個源信號寫成一維向量形式為

S= [s1(1),s1(2),…，s1(T);s2(1),s2(2),…，s2(T);

…;sN(1),sN(2),…，sN(T)]T

(3)

M個觀測信號寫成一維向量形式為

X= [x1(1),x1(2),…，x1(T);x2(1),x2(2),

…，x2(T);…;xM(1),xM(2),…，xM(T)]T

(4)

式中T為微地震信號長度。

那么源信號S和觀測信號X的一維向量關系可表示為

(5)

式中

(6)

式(5)就是獨立變量分析中轉換矩陣方程，其中E=[Eij]∈RM×T×N×T是轉換矩陣或混合矩陣。

在壓縮感知理論下，源信號S在一組基下可稀疏表示為

(7)

式中：Ψ=[φ1,φ2,…,φM]為基向量，α為系數向量。對于給定觀測信號X和測量矩陣Φ，尋找源信號S，使

X=ΦΨα

(8)

且滿足在某組稀疏基Ψ的作用下S=Ψα。在一般的壓縮感知算法中要求測量矩陣Φ為已知，設計為隨機矩陣的形式，而且稀疏基Ψ也已知，即在傳感矩陣Θ=ΦΨ已知的前提下設計各種優化算法來估計源信號的稀疏表示α，然后通過變換S=Ψα得到源信號[21-24]。

要恢復或重建源信號，測量矩陣Φ和稀疏基矩陣Ψ的設計是關鍵。測量矩陣一般流行的設計方法是采用隨機高斯矩陣。這種方法設計的測量矩陣，在數學上滿足了其和基正交的條件，同時也滿足了壓縮感知的RIP條件。如果觀測信號噪聲成分較多，這時利用以上方法設計測試矩陣，重建源信號的效果較差。因此，采用獨立變量分析方法進行測量矩陣設計，即對觀測信號進行獨立變量分析，建立正交的測量矩陣。

3 混合矩陣估計與稀疏化

獨立分量分析中的關鍵問題是混合矩陣的估計，為了得到混合矩陣的最優估計，混合矩陣的正交化和稀疏化是獲得混合矩陣最優估計的核心。

3.1 混合矩陣的正交化方法

對于微地震信號提取而言，矩陣的正交化涉及兩方面的問題： 一是如何組成正交化矩陣； 二是對已有矩陣如何正交化。正交化的目的： ①滿足算法自身的要求條件； ②得到獨立的正交分量。矩陣正交化后得到的獨立分量是正交的，但未必是期望的正交分量。對于微地震信號提取問題，目的是得到期望正交分量。為此，需要討論從觀測的微地震資料中如何構建正交化混合矩陣。

3.1.1 數據組合正交化

(1)去均值化處理；

(2)在微地震信號滿足最小相位或準最小相位的條件下，通過頻譜分析獲得微地震子波主頻，根據主頻大小確定時窗長度；

(3)把整個時窗長度為W的微地震信號，分成P段，研究發現取P=3較合適，并且段與段之間有一定重疊；

(4)對相鄰道進行分段，為了避免相鄰道數據的相關問題，相鄰道數據選取錯開一定的時移。

3.1.2 自適應最佳獨立分量個數估計

獨立分量的個數就是測量矩陣的維數，測量矩陣維數的大小與稀疏度密切相關。因此，確定合適獨立變量個數至關重要。

對信號進行獨立分量分析處理，計算不同道的分解分量相關系數，對任意兩道的L個分量兩兩計算相關系數，找出相關系數最大時對應的兩個分量，然后對多道依此計算，找出多道相關系數最大時對應的分量[25]。如果混合矩陣的維數(分量的個數)選取不合適，就有可能提取不到有用信號。為此，設計自適應方法，自動調整計算不同維數分量的多道相關系數，當維數取得合適時，多道有用信號分量的相關系數最大，進而分離出有效弱信號。

3.2 混合矩陣的稀疏化方法

稀疏化的本質是從混合信號中辨識出混合矩陣中各列的期望方向。有的信號在當前狀態下(時間序列)稀疏化(同域稀疏化)不明顯，但是如果把該信號轉換到其他域如頻率域，稀疏化(變換域稀疏化)就明顯了[26]。

線性變換后混合矩陣的形式不會發生變化，則式(1)經過變換后可以表示為

Γ[X(t)]=Γ[AS(t)]=AΓ[S(t)]

(9)

(10)

如何選取線性變換Γ(·)是問題的重點與難點。盡管短時Fourier變換可以使某些信號更加稀疏，但是由于涉及到如何選取時窗函數和時窗的寬度及重合度等問題，往往不能得到最優的表示。壓縮感知對信號具有較強的稀疏化能力，但是在稀疏化過程中往往疏漏了一些弱信號的成分，而獨立分量分析能把各種信號相對較全面地揭示出來，但是獨立分量過度稠密降低了對有效信號分析的能力，二者結合進行信號稀疏化可取得較好的效果[27]。

圖1為原始地震資料，圖2為小波變換去噪處理結果，圖3為獨立分量分解小波去噪結果。對比圖1～圖3可以發現，小波變換方法在微地震資料去噪方面有一定效果，但是對一些區域性噪聲壓制作用有限和對高頻信號的揭示能力也不夠強，但獨立分量對有效信號具有很好的揭示能力。對比圖3a與圖3b可以發現，組合矩陣正交化后能夠得到獨立的正交分量，可以很好地分離出有效信號、壓制區域噪聲，提高了微地震資料的信噪比。

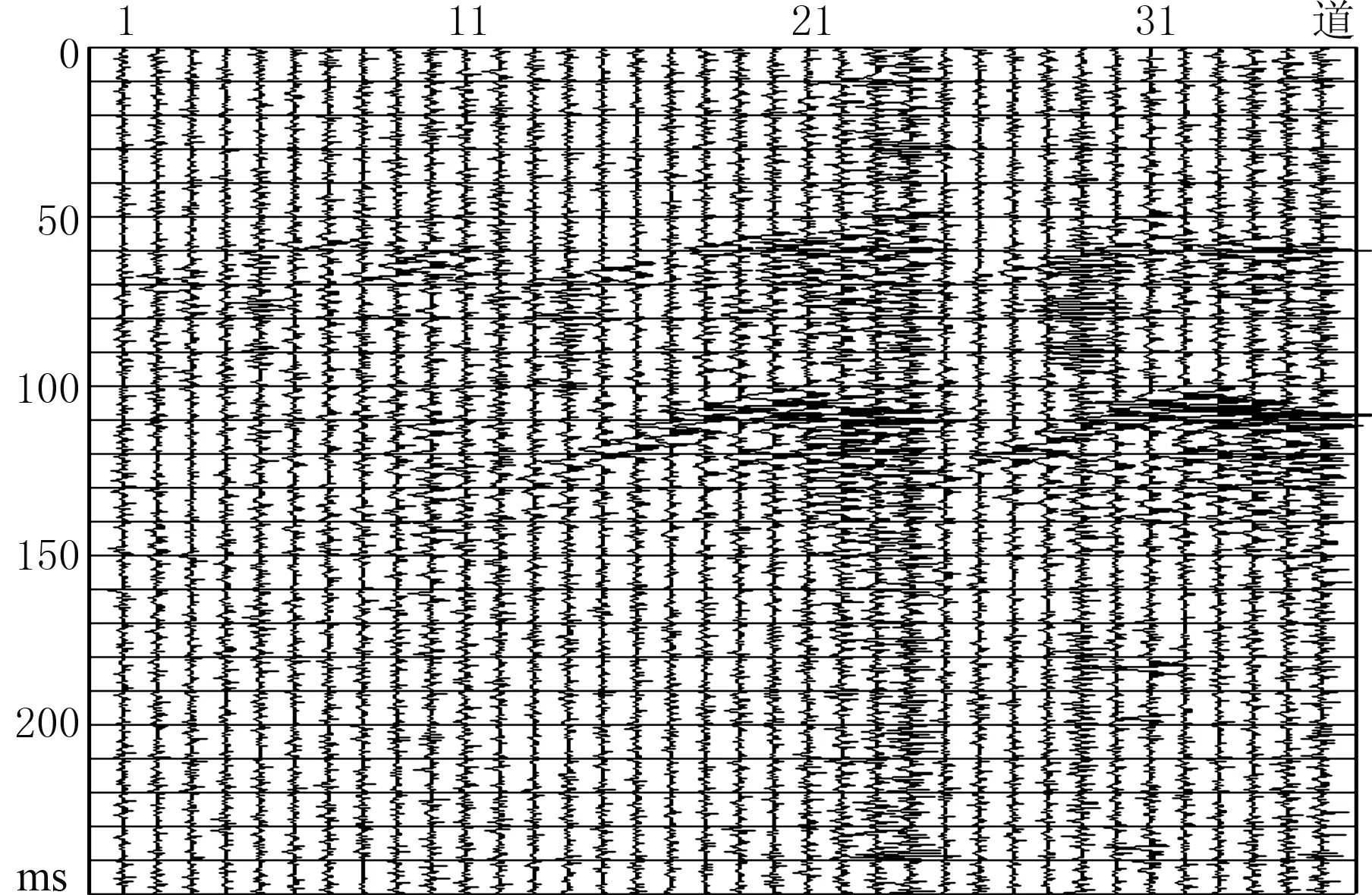
圖1 原始微地震資料

圖2 小波變換噪聲壓制方法處理結果

4 信號重建的唯一性問題

決定重構源信號所需要的測量值的數目是由信號的稀疏度決定的。在給定稀疏度的前提下，一個信號可以有不同的表示方式。但是，總存在一種稀疏度最小情形，把這種情況定義為信號的最稀疏表示。顯然，信號的最稀疏表示是唯一的。

研究發現，隨著測量值數目的增加，恢復的信號與原信號的絕對誤差越來越小，直到測量值數目大于某一特定值時，就能充分恢復原信號。顯然，稀疏度越大，完全重構信號需要的測量值越多。當信號的稀疏度越大時，成功重構信號需要的測量值數目越多，而且隨著測量值數目的增加，能夠成功重構的信號越來越多，直到全部信號都能成功恢復，即信號成功重構的概率趨近于1。

為了進一步討論微地震信號壓縮感知重建特別是微地震弱信號重建問題，有必要引入稀疏率概念，假設信號的長度為I，稀疏度為K，則稀疏率λ表示為信號長度和稀疏度的比值，即λ=K/I。微地震反射信息不論是強信號還是弱信號都是一定長度的微地震子波和地層傳播響應的綜合結果，通過壓縮感知方法，雖然通過變換域的方法增強了這些疊加的弱信號的稀疏性，但是如果稀疏度和稀疏率選取不合適，仍然得不到弱信號重建的真解。根據微地震子波特性，如果稀疏域是頻域，則I的長度取地震子波長度的2倍(地震子波補零擴展)。圖4為圖1數據在不同稀疏率下的壓縮感知重建結果，圖5為不同稀疏率的基于獨立分量分析和壓縮感知的重建結果，可以發現相互耦合的弱信號和噪聲通過盲分離(獨立分量分析)實現了解耦，增強了對微地震信號進行稀疏化的能力。通過大量試算可知，稀疏率取0.1～0.2較為合適。

圖3 獨立變量分析方法噪聲壓制結果

圖4 不同稀疏率下壓縮感知微地震信號重建結果

圖5 不同稀疏率下基于獨立分量分析和壓縮感知微地震信號重建結果

5 實際資料處理結果分析

通過對混合矩陣的正交化以及稀疏率的選取，實現了獨立分量壓縮感知微地震弱信號提取重建的方法。為了驗證方法的應用效果，對實際微地震資料進行了試算，結果如圖6所示。由圖可見，獨立分量與壓縮感相結合的處理方法除了增強微地震弱信號之外，還較好地提取出了淹沒在噪聲中的有效信號，說明了該方法的有效性。A地區微地震資料中、上部的干擾信號得到了很好的壓制；B地區微地震資料處理結果不僅壓制了區域的干擾噪聲，還提取出了部分被淹沒的有效信號，凸顯了初至信號，大大提高了微地震資料的信噪比，有利于初至信號的拾取；C地區微地震資料的上部、下部的干擾噪聲得到了壓制，凸顯了中部有效信號。不同地區的微地震資料的試算結果都說明，獨立分量與壓縮感相結合的處理方法能取得很好的處理效果，具有廣泛的適用性。

圖6 不同地區實際微地震資料處理前(左)、后(右)對比

6 結論

微地震弱信號具有較強的模糊性和較差的稀疏性，直接通過壓縮感知技術進行弱信號的提取難以取得理想的效果。獨立分量分析(盲源分離分析)方法，雖然具有較強的信號分離能力，但是分離的有效信號具有一定的不確定性。本文結合兩種方法的特點，提出了獨立分量壓縮感知弱地震信號提取方法，較好地實現了微地震弱反射信號的提取。

(1)在混合矩陣估計過程中，根據微地震記錄數據特征，合理地組合觀測矩陣，盡量使矩陣正交化，這種考慮數據結構組成的正交化矩陣減小了分離有效獨立分量的不確定性。

(2)針對獨立變量分析混合矩陣的維數確定關鍵問題，設計了自適應方法，能夠較準確地確定混合矩陣的維數。

(3)基于稀疏度、稀疏率和微地震波傳播特征綜合考慮稀疏度的選取，增強了弱信號提取的可靠性。

[1] 孟小紅，吳何珍，劉國峰.盲源反褶積方法與應用研究.石油地球物理勘探，2005，40(6)：642-645. Meng Xiaohong，Wu Hezhen，Liu Guofeng.Study of blind deconvolution and application of method.OGP，2005，40(6)：642-645.

[2] 宋維琪，楊勤勇，郭全仕等.地面微地震資料弱信號提取方法研究.石油物探，2013，52(2)：131-135. Song Weiqi，Yang Qinyong，Guo Quanshi et al.Weak signal extraction method for surface microseismic monitoring data.GPP，2013，52(2)：131-135.

[3] 戴瓊海，付長軍，季向陽.壓縮感知研究.計算機學報，2011，34(3)：425-434. Dai Qionghai，Fu Changjun，Ji Xiangyang.Research on compressed sensing.Chinese Journal of Computers，2011，34(3)：425-434.

[4] Candès E，Wakin M.An introduction to compressive sampling.IEEE on Signal Processing Magazine，2008，25(2)：21-30.

[5] Donoho D，Tsaig Y.Extensions of compressed sen-sing.Signal Processing，2006，86(3)：533-548.

[6] 印興耀，劉杰，楊培杰.一種基于負熵的Bussgang地震盲反褶積方法.石油地球物理勘探，2007，42(5)：499-505. Yin Xingyao，Liu Jie，Yang Peijei.A negative entropy-based Bussgang seismic blind deconvolution.OGP，2007，42(5)：499-505.

[7] 劉喜武，高偉，張寧等.基于帶狀混合矩陣ICA實現地震盲反褶積.地球物理學進展，2007，22(4)：1153-1163. Liu Xiwu，Gao Wei，Zhang Ning et al.ICA with banded mixing matrix based seismic blind deconvolution.Progress in Geophysics，2007，22(4)：1153-1163.

[8] 高偉.基于獨立變量分析的盲反褶積研究[學位論文].山東青島：中國海洋大學，2011. Gao Wei.Blind Deconvolution Based on Independent Component Analysis[D].Ocean University of China，Qingdao，Shandong，2011.

[9] 王維強.獨立分量分析在地震勘探中的應用研究[學位論文].山東青島：中國石油大學(華東)，2012. Wang Weiqiang.Application of Independent Component Analysis in Seismic Exploration[D].China University of Petroleum (East China)，Qingdao，Shandong，2012.

[10] Wadayama T.Sufficient condition for perfect recovery in compressed sensing.The Brain & Neural Networks，2010，17(2)：63-69.

[11] Pennec E L，Mallat S.Sparse geometrical image representation with bandelets.IEEE Transactions on Image Processing，2005，14(4)：423-438.

[12] 周燦梅.基于壓縮感知的信號重建算法研究[學位論文].北京：北京交通大學，2010. Zhou Canmei.Research on Signal Reconstruction Algorithms Based on Compressed Sensing[D].Beijing Jiaotong University，Beijing，2010.

[13] Baraniuk R G，Cevher V，Duarte M F et al.Model based compressive sensing.IEEE Transactions on Information Theory，2010，56(4)：1982-2001.

[14] Gholami A.Non-convex compressed sensing with frequency mask for seismic data reconstruction and denoising.Geophysical Prospecting，2015，62(6)：1389-1405.

[15] 周亞同，王麗莉，蒲青山.壓縮感知框架下基于K-奇異值分解字典學習的地震數據重建.石油地球物理勘探，2014，49(4)：652-660. Zhou Yatong，Wang Lili，Pu Qingshan.Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework.OGP，2014，49(4)：652-660.

[16] 郭樹旭，張馳，曹軍勝等.基于壓縮感知歸一化關聯成像實現目標重構.光學精密工程，2015，23(1)：288-294. Guo Shuxu，Zhang Chi，Cao Junsheng et al.Object reconstruction by compressive sensing based normalized ghost imaging.Optics and Precision Engineering，2015，23(1)：288-294.

[17] 方紅，楊海蓉.貪婪算法與壓縮感知理論.自動化學報，2011，37(12)：1413-1421. Fang Hong，Yang Hairong.Greedy algorithms and compressed sensing.Acta Automatica Sinica，2011，37(12)：1413-1421.

[18] Yin H，Li J，Chai Y et al.A survey on distributed compressed sensing：theory and applications.Frontiers of Computer Science，2014，8(6)：893-904.

[19] 郭科，郭思,何國柱等.基于獨立分量分析的多次波盲分離方法研究.地球物理學進展，2010，25(3)：1075-1080. Guo Ke，Guo Si，He Guozhu et al.A method of multiple blind separation based on ICA.Progress in Geophysics，2010，25(3)：1075-1080.

[20] 謝忠德.基于稀疏表示的盲信號分離算法研究[學位論文].廣東廣州：廣東工業大學，2012. Xie Zhongde.Study on Blind Signal Separation Algorithm Based on Sparse Representation [D].Guang-dong University of Technology，Guangzhou，Guangdong，2012.

[21] Donoho D L.Compressed sensing.IEEE Transactions on Information Theory，2006，52(4)：1289-1306.

[22] Candes E J，Romberg J，Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory，2006，52(2)：489-509.

[23] 王新全，耿瑜，Ru-shan Wu等.基于壓縮感知的Drea-mlet域數據重構方法及應用.石油地球物理勘探，2015，50(3)：399-404. Wang Xinquan，Geng Yu，Ru-shan Wu et al.Seismic data reconstruction in Dreamlet domain based on compressive sensing.OGP，2015，(3)：399-404.

[24] 白蘭淑，劉伊克，盧回憶等.基于壓縮感知的Curvelet域聯合迭代地震數據重建.地球物理學報，2014，57(9)：2937-2945. Bai Lanshu，Liu Yike Lu Huiyi et al.Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing.Chinese Journal of Geophysics，2014，57(9)：2937-2945.

[25] 呂文彪，尹成,張白林等.利用獨立分量分析法去除地震噪聲.石油地球物理勘探，2007，42(2)：132-136. Lv Wenbiao，Yin Cheng，Zhang Bailin et al.Using in-dependent component analysis to noise.OGP，2007，42(2)：132-136.

[26] 李穩，劉伊克，劉保全等.基于稀疏分布特征的井下微地震信號識別與提取方法.地球物理學報，2016，59(10)：3869-3882. Li Wen，Liu Yike，Liu Baoquan et al.Downhole microseismic signal recognition and extraction based on sparse distribution features.Chinese Journal of Geophysics，2016，59(10)：3869-3882.

[27] Bruckstein A，Donoho D，Elad M.From sparse solutions of systems of equations to sparse modeling of signals and images.SIAM Review，2009，51(1)：34-81.

(本文編輯：宜明理)

宋維琪 教授，博士生導師，1964年生; 1987年畢業于長春地質學院應用地球物理專業，獲學士學位；1996年畢業于中國石油大學(華東)應用地球物理專業，獲碩士學位；2002年畢業于中國石油大學(華東)應用地球物理專業，獲博士學位；現在中國石油大學(華東)地球物理系從事地球物理方面的教學和科研，主要研究領域包括地震儲層預測和壓裂微地震監測等。

1000-7210(2017)05-0984-06

P631

A

10.13810/j.cnki.issn.1000-7210.2017.05.011

*山東省青島市黃島區長江西路66號中國石油大學(華東)地球科學與技術學院，266580。Email：swq1123@126.com

本文于2016年6月15日收到，最終修改稿于2017年8月9日收到。

本項研究受國家科技重大專項“水力壓裂實時監測與地質工程一體化評估技術”(2016ZX05023-004)資助。