有限元強度折減法應用的幾個問題及拓展

陳子玉，宋彥輝,2，嚴 豪

(1.長安大學 地質工程與測繪學院， 陜西 西安 710054； 2.西部礦產資源與地質工程教育部重點實驗室， 陜西 西安 710054)

有限元強度折減法應用的幾個問題及拓展

陳子玉1，宋彥輝1,2，嚴 豪1

(1.長安大學 地質工程與測繪學院， 陜西 西安 710054； 2.西部礦產資源與地質工程教育部重點實驗室， 陜西 西安 710054)

隨著計算機技術的發展，有限元強度折減法作為邊坡穩定性分析的重要工具日益得到重視。介紹有限元強度折減法的應用和發展現狀，以及強度折減法的原理。采用有限元強度折減法對網格密度、坡型、斜坡變形及破壞機理進行了研究，并與極限平衡法進行了對比。結果表明：有限元網格密度越大與極限平衡法越接近；不規則坡形會降低斜坡穩定性；采用強度折減法可以清楚地展示斜坡的破壞過程和機理，為預測和監控斜坡土體破壞提供了一條新的途徑。

有限元；強度折減法；穩定分析；破壞機制

有限元強度折減法作為一種數值模擬的方法，相較于傳統的極限平衡法，在分析邊坡的變形破壞時其不需要事先假定的滑動面，且可以清晰地計算邊坡巖土體內部的應力變化，因此在邊坡穩定性分析領域得到了越來越多的重視[1-2]。21世紀，隨著FLAC3D、ABAQUS等有限元軟件的開發及計算機計算能力的提高[3-4]，有限元強度折減法才得以大規模應用。國內鄭穎人院士等對有限元強度折減法的理論模型、失穩判據、在地基中的拓展、可靠性分析等方向進行了詳細研究[5-10]。這些研究表明有限元強度折減法可以有效分析邊坡穩定性，并且較傳統方法更易模擬，為進一步的研究和應用奠定了良好的基礎。

在已有研究基礎上，本文進一步探討了SSR方法在分析斜坡穩定性方面與極限平衡法間存在的差異及應注意的問題，同時對該法在研究斜坡變形破壞機理上進行了分析，以拓展有限元強度折減法的應用領域。

1 有限元強度折減法的基本原理

有限元強度折減法的計算原理是在計算時先假定折減系數F，從而降低巖土體整體的強度參數，即：

cF=c/F

(1)

ФF=arctan(tanФ/F)

(2)

通過不同的折減系數F，計算機程序采用最小二乘法計算最終的折減系數F，當計算結果不能滿足巖土體的應力平衡，巖土體的應力應變出現突變，邊坡內部產生塑形貫通，巖土體邊坡此時的狀態對應于邊坡的極限平衡狀態。

2 有限元強度折減法在斜坡穩定分析中的問題

2.1 與極限平衡法的比較

傳統的極限平衡法在計算斜坡的穩定系數時不考慮斜坡內應力-應變場的分布，而只根據斜坡巖土體內下滑力(或力矩)與抗滑力(或力矩)的計算來實現。因此，除均一的土質斜坡或似均質斜坡可采用自動搜索滑動帶外，其它情況均需要地質工程師根據實際地質情況事先給定破壞滑動面，然后以此為基礎運用力的平衡條件計算斜坡穩定系數。有限元強度折減法則是通過計算斜坡巖土體單元的應力-應變分布，通過參數強度折減方法逐漸自動獲取斜坡巖土體的最大剪切應變屈服帶，是一種應力-應變控制的計算方法。因此該方法不需要事先確定潛在破壞面的位置，而由計算程序自動按照斜坡巖土體單元的應力應變來確定，因此該方法從本質上更符合斜坡體的演變規律。但是，在應用該方法時，尚有一些問題值得考慮和注意，如計算中斜坡失穩的判據[11]、計算參數的選取[12]、計算結果與傳統極限平衡法的差異[13]及計算中存在的其它問題等[10]。

2.1.1 不同單元尺寸對穩定系數計算的影響

通常，研究兩種方法計算結果的差異，應從最簡單的實例開始，這樣更容易得到差別所在并有助于分析其可能的原因。據此，分別以15 m、30 m、60 m的均質土質邊坡為例，坡角分別采用45 ° 和60 °，利用Rocscience公司開發的RS2有限元程序及極限平衡法分別進行計算，其中RS2程序采用摩爾-庫侖破壞準則，以最大剪切應變帶反映斜坡的最終破壞面，設定程序的最大迭代次數為500，計算精度為0.01，當折減系數達某一值而使計算不能收斂時，即認為斜坡已沿潛在最大剪切應變帶產生屈服并開始產生破壞。

表1為計算采用的土質斜坡的參數，表2為采用兩種不同方法計算的結果，圖1為有限元網格模型。

從表2可以看出，強度折減法的計算結果與有限元模型的網格單元大小有較大關系。當采用粗網格時(單元網格尺寸大于5 m2)，穩定性系數與極限平衡法相差較大，采用一般網格單元時(單元網格尺寸約1.5 m2～2.0 m2)，計算的穩定系數均高于極限平衡法，高出幅度約11%～14%；當采用高密度單元時(單元網格尺寸小于1 m2)時，有限元強度折減法計算的斜坡穩定系數與極限平衡法基本一致。這表明在有限元強度折減法中，單元網格的劃分對計算結果有直接影響，網格越密，計算精度越高，計算結果越接近極限平衡法。

表1 計算土坡的物理力學參數

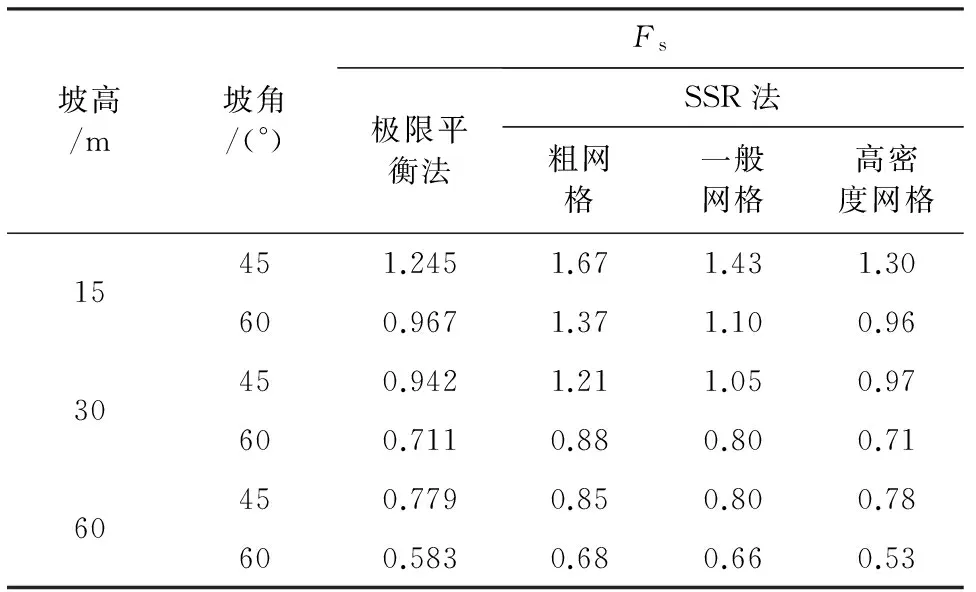
表2 不同方法計算結果

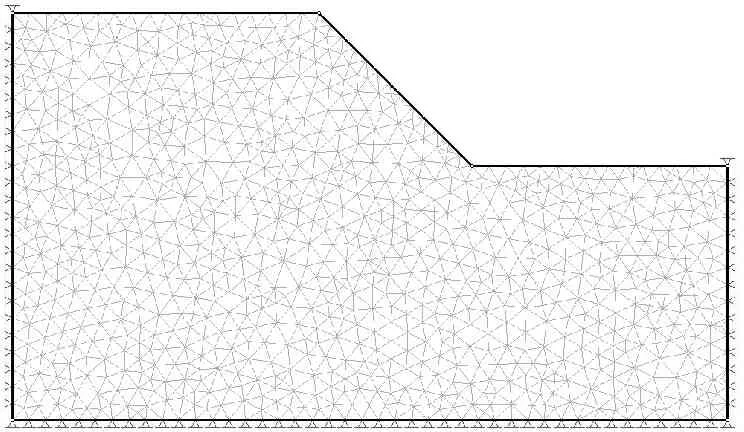
圖1有限元網格模型

2.1.2 計算滑面位置的比較

傳統極限平衡法對均質土坡按斜坡下滑所需的最小力矩平衡來確定滑面位置，常采用試算搜索法。而有限元強度折減法則按照斜坡巖土單元應力-應變的發展來確定最終破壞路徑。為比較兩者的差別，以前述坡高60 m、坡角45 ° 的斜坡為例進行了分析。

結果表明，不同密度網格單元計算的滑面位置基本接近，網格越大，剪切應變帶越粗，如圖2～圖4所示。但SSR法計算滑面與極限平衡法稍有差別(圖中黑色圓弧線為極限平衡法計算滑動面)。一般規律是，極限平衡法計算的滑面后壁位置較SSR法更靠近坡緣，而且除坡度較大的斜坡外滑面一般均通過坡腳剪出，而SSR計算結果則往往在坡腳以上屈服，且網格單元越大，剪出口位置越高，最大剪切應變帶距離坡腳越遠；在坡體內部兩種方法計算滑面的位置基本一致，滑面接近重合；在靠近坡頂部位，SSR法計算的坡頂最大應變帶較極限平衡法靠后。出現以上差別的原因是因為有限元強度折減法對斜坡整體的強度參數進行了折減，導致折減過程中剪切應變帶區域較大[14]，因此計算出的滑面位置較極限平衡法更靠后。計算結果還表明，網格單元越密，兩種方法計算的滑面位置越接近，且最終計算的穩定性系數也越接近。網格單元越大(粗網格)剪應變帶越寬，滑面位置與極限平衡方法相比有時差別較大(見圖4)。

圖2 一般網格單元計算的最大剪應變帶

圖3高密網格單元計算的最大剪應變帶

2.2 不規則坡形對有限單元折減法計算的影響

由于有限元強度折減法的計算特性，當斜坡土體內某一處的計算結果不收斂或者出現塑形貫通時，計算終止而求得邊坡的穩定性系數，此時忽略了斜坡的整體穩定性[15]，尤其對斜坡坡形復雜或由多層巖土介質組成的斜坡更應注意。當斜坡坡形僅有很小的變化時，其穩定性系數的計算結果較規則邊坡有較大區別，此時應分別考慮斜坡局部穩定性和整體穩定性。

圖4粗網格單元計算的最大剪應變帶

圖5為某不規則坡面均質土坡在應用SSR方法計算坡體穩定性時的計算結果，圖6通過限定強度折減范圍來考慮斜坡整體穩定性。結果表明，斜坡會在斜坡局部發生破壞(圖5中Fs=0.62)，破壞位置位于坡面形狀臺階形變化處，坡體在此處應力集中形成剪出口，使得坡體發生局部破壞。但對于斜坡整體而言，其破壞有時不僅僅發生在淺表層，內部由于土體長期蠕變等影響也會發生破壞，而有限元強度折減法應用于不規則坡形時，最先達到不穩定狀態的部位一般處在斜坡的坡面變化處，對斜坡整體穩定性的考慮不足。為了解決這一問題可以對坡體限定強度折減范圍，計算出土坡整體上也處于不穩定狀態(圖6中Fs=0.71)，此時剪出口位置變化到坡腳。因此當對不規則坡面斜坡進行設計治理時，僅根據圖5結果進行治理設計，將會產生嚴重的誤導。

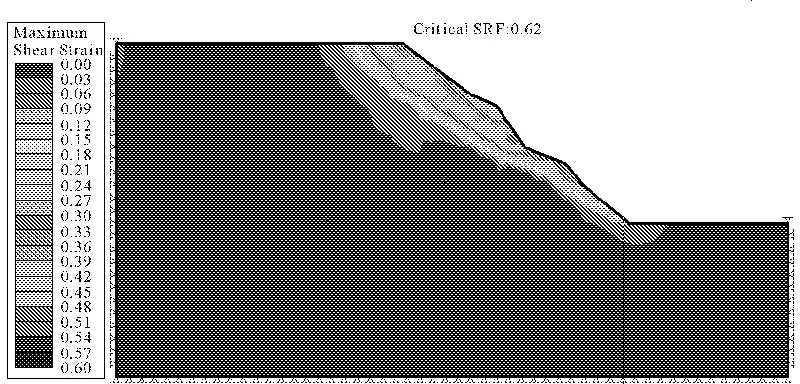
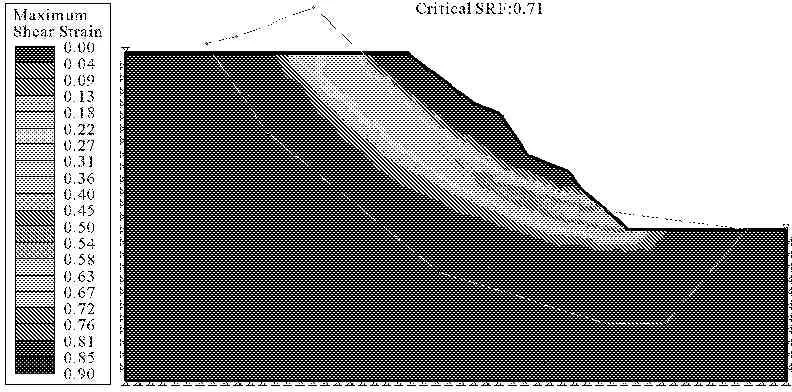
圖5 坡形對計算結果的影響

圖6斜坡整體穩定性計算

3 有限元強度折減法對斜坡變形破壞機制的研究

有限元強度折減法在計算過程中通過不斷改變折減系數來降低或增大巖土抗剪強度c、φ值從而使斜坡巖土體達到極限平衡狀態。這一計算模擬過程反映了斜坡巖土材料強度在同步折減條件下不斷屈服直至達到臨界狀態的過程。在這一系列過程中，如果將每一次折減的計算結果保存下來，就可以看到，隨著折減系數的變化，斜坡巖土體內的最大剪切應變等值線也在不斷變化，并最終形成統一的剪切滑動帶，這一過程充分反映了斜坡變形破壞的演化進程和破壞機制，對理解斜坡失穩方式及治理設計方案具有重要作用。

對巖質邊坡而言，由于受軟弱結構面的影響，屈服往往首先在不連續面及軟弱巖性中產生，隨著折減系數的增大，可以明顯看到最大剪切變形的發展趨勢直至形成統一的破壞面。圖7為一水平層狀砂巖和泥巖形成的斜坡，斜坡高60 m，坡度45 °。斜坡上部及基座為砂巖，靠近坡腳部位為相對軟弱的泥巖，整個斜坡巖體結構除水平層面外，尚發育一組與層面垂直的短小節理。

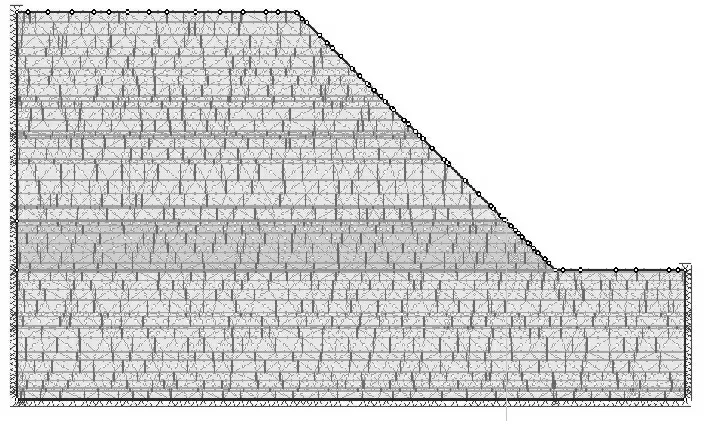
圖7某巖質斜坡結構模型

圖8～圖11為采用有限元強度折減法計算的不同折減系數下斜坡體內最大剪切應變等值線。從圖中可以看出，隨著折減系數F的增大，即巖土參數不斷弱化，最大剪切應變帶在不斷變化，由最初的坡腳泥巖向坡內及上方發展的同時，發生在坡頂的最大剪切應變帶也逐漸呈弧形向下發展，并最終貫通形成潛在滑移破壞面(見圖10、圖11)。并且隨著折減系數取值的增大，最大應力等值線發展速度隨之增加。

這一模擬計算過程清楚地顯現了該斜坡的破壞演化過程及潛在破壞面的形狀及位置，該過程與巖質邊坡實際破壞過程相符。強度折減法不僅可以求得巖質斜坡的穩定性系數，還可以計算出某一折減系數下坡體內部剪切應變帶的發展趨勢和應變量，為邊坡的防護治理提出針對性的方案，從而更好地為工程服務。

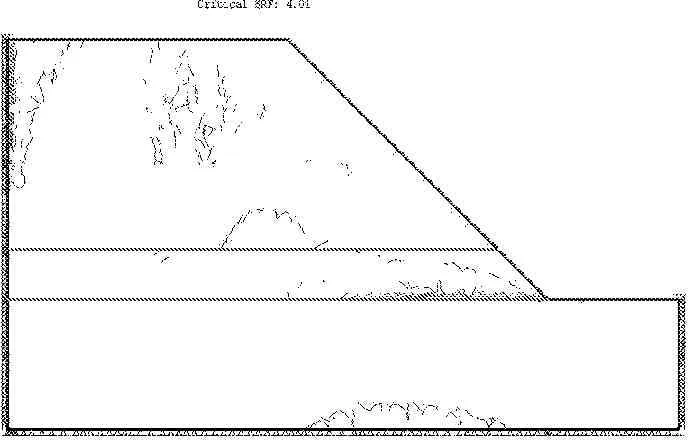
圖8 最大剪切應變等值線(折減系數為3.0)

圖9 最大剪切應變等值線(折減系數為3.6)

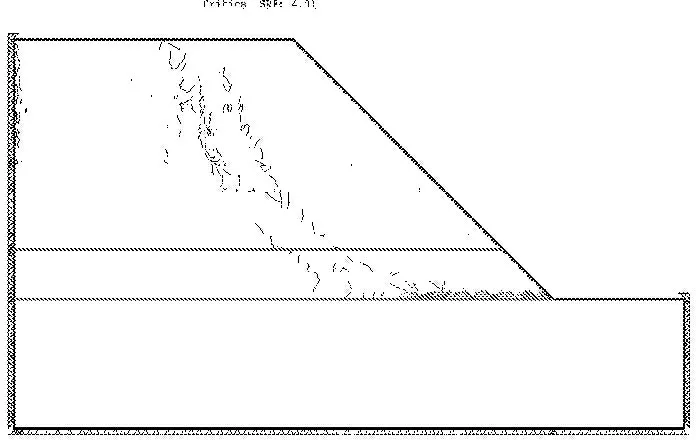
圖10 最大剪切應變等值線(折減系數為4.0)

圖11最大剪切應變等值線(折減系數為4.09)

4 結 論

(1) 有限元強度折減法廣泛應用于斜坡穩定性的研究，不僅適用于簡單的土質斜坡，同樣可以應用于復雜的巖質邊坡。但在應用過程中應注意單元網格的劃分對計算結果的影響。研究表明，計算時應盡最大可能采用較小的網格單元，這樣才能使計算結果及模擬的潛在滑面位置更加準確。

(2) 有限元強度折減法在斜坡穩定性計算中，強度折減法所求剪切應變帶和極限平衡法所求滑動面位置有區別，網格劃分越細，兩者越接近一致，網格較粗時有較大誤差。

(3) 當斜坡坡形復雜或計算由多層介質組成的斜坡穩定性時，不僅要注意斜坡局部的屈服破壞，而且要研究斜坡的整體穩定性，只有這樣才能正確了解斜坡的穩定狀況，從而為治理設計提供可靠的依據。

(4) 有限元強度折減法作為一種強有力的計算方法，不僅可以計算斜坡的穩定狀態，而且可以模擬斜坡的變形破壞演化過程及機理，從而使設計者能夠根據斜坡目前的穩定狀況及其演變趨勢有效地采取相應的應對措施。

[1] Matsui T，San K C. Finite element stability analysis method for reinforced slope cutting[J]. Proceeding International Geotechnical Symposium on Theory and Practice of Earth Reinforcement,1988,26(1)：317-322.

[2] Matsui T，San K C .Finite element slope stability analysis by shear strength reduction technique[J]. Soils and Foundations, 1992,32(1)：59-70.

[3] 高長勝，陳生水，楊守華，等.基于強度折減有限單元法的抗滑樁加固邊坡特性分析[J].水利與建筑工程學報,2010,8(4):119-122.

[4] 楊林青,王忠濤，李家鋼，等.基于強度折減理論的海底斜坡穩定性分析[J].水利與建筑工程學報,2012,10(6):26-30.

[5] 鄭穎人,趙尚毅，宋雅坤.有限元強度折減法研究進展[J].水利與建筑工程學報,2005,3(1):1-6.

[6] 陳力華,靳曉光.有限元強度折減法中邊坡三種失效判據的適用性研究[J].土木工程學報,2012,45(9):136-146.

[7] 孔位學,鄭穎人，趙尚毅，等.地基承載力的有限元計算及其在橋基中的應用[J].土木工程學報,2005,38(4):97-102.

[8] 施建勇,曹秋榮，周璐翡.修正有限元強度折減法與失穩判據在邊坡穩定分析中的應用[J].巖土力學,2013,34(S2):237-241.

[9] 吳應祥,劉東升，宋強輝.基于有限元強度折減法的邊坡動力穩定性可靠性分析[J].巖土力學,2013,34(7):2084-2090.

[10] 喻和平,袁明明，張 聰，等.基于彈塑性區間有限元的邊坡穩定性分析[J].水利與建筑工程學報,2016,14(2):132-135.

[11] 裴利劍, 屈本寧，錢閃光.有限元強度折減法邊坡失穩判據的統一性[J].巖土力學,2010,31(10):3337-3341.

[12] 潘新恩.強度折減法計算邊坡穩定性中彈性模量和泊松比的取值研究[J].水利與建筑工程學報,2014,12(4):55-59.

[13] 王學鵬.滑坡體穩定分析的極限平衡法與有限元法對比研究[D].昆明：昆明理工大學,2015:41-57.

[14] 陳國慶,黃潤秋，石玉川，等.基于動態和整體強度折減法的邊坡穩定性分析[J].巖石力學與工程學報,2014,33(2):243-256.

[15] 李 躍,楊永生，毛權生，等.基于三維地質模型的排土場邊坡整體穩定性探究[J].巖土力學,2013,34(S1):533-539.

ApplicationIssuesofFiniteElementShearStrengthReductionMethod

CHEN Ziyu1, SONG Yanhui1,2, YAN Hao1

(1.CollegeofGeologyEngineeringandGeomatics,Chang'anUniversity,Xi'an,Shaanxi710054,China; 2.KeyLaboratoryofWesternMineralResourcesandGeologicalEngineeringMinistryofEducation,Xi'an,Shaanxi710054,China)

With the development of computer technology, the finite element strength reduction method has been paid more and more attention as an important tool for slope stability analysis. In this paper, the application and development of finite element strength reduction method and the principle of strength reduction method are introduced first. Then the finite element strength reduction method are adopted to study the mesh density, slope shape, slope deformation and failure mechanism, and compared with the limit equilibrium method. The results show that the larger the mesh density of the finite element is, the closer the limit equilibrium method; irregular shape of slope will reduce the slope stability; this method can clearly show the failure process and mechanism, thus provides a new way for the prediction and monitoring of slope failure.

finiteelementmethod;shearstrengthreduction;stabilityanalysis;failuremechanism

10.3969/j.issn.1672-1144.2017.05.036

2017-04-30

2017-06-04

陳子玉(1992—)，男，安徽淮北人，碩士研究生，研究方向為地質工程、地質災害、基坑工程等。E-mail:chdgcdz@163.com

TU42

A

1672—1144(2017)05—0196—05