函數項級數一致收斂柯西判別法的改進形式

邢家省，楊義川

(1.北京航空航天大學數學與系統科學學院，北京100191；2.數學、信息與行為教育部重點實驗室, 北京100191)

函數項級數一致收斂柯西判別法的改進形式

邢家省1,2，楊義川1,2

(1.北京航空航天大學數學與系統科學學院，北京100191；2.數學、信息與行為教育部重點實驗室, 北京100191)

考慮函數項級數和含參變量廣義積分的一致收斂性的判別問題，經典的柯西準則判別法是證明函數項級數和含參變量廣義積分一致收斂的有效方法，然而應用柯西準則判別函數項級數和含參變量廣義積分非一致收斂時，對每一個問題都要給出各自具體細致的操作過程，相當的繁瑣，沒有形成系統的理論方法。經過對經典的柯西準則的表述方式給予改進，利用改進表述的柯西準則，給出了函數項級數和含參變量廣義積分的非一致收斂性的一般性方法，敘述簡便，通過實例說明改進的柯西準則的表述方法的技術指引性和對在具體問題使用中的簡潔性，容易掌握并有利于傳播。

函數項級數；含參變量廣義積分；一致收斂性；柯西準則；非一致收斂

函數項級數和含參變量廣義積分的一致收斂性的判別問題是數學分析中的重要內容，經典的柯西準則判別法是證明一致收斂的常用有效方法[1-8]。在經典文獻[1-8]中，應用柯西準則判別非一致收斂時，是對每一問題給出一個表述過程，各不相同，表述過程和具體操作顯得有點繁瑣，沒有形成一套理論方法。在綜合文獻[1-19]中的思想方法的基礎上，發現可以對經典的柯西準則的表述方式給予改進，利用改進的柯西準則，給出了證明一些函數項級數和含參變量廣義積分的非一致收斂性的一般性方法，通過大量實例證明改進的表述方法的技術指引和在具體使用中的簡便性，以理論方法統一的形式傳播，達到數學分析學中應有的理論高度。

1 函數項級數一致收斂柯西準則的改進形式

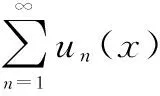
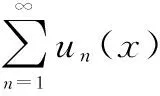
|SnN+pN(xN)-SnN(xN)|≥ε0。

定理2是證明函數項級數非一致收斂的常用方法，然而應用此方法時，需要每一個問題就要給出一個具體的敘述過程，表述非常的繁瑣，沒有體現出技術指引性。可以將定理1的結果的表述形式給予改進，改進后的形式方便于使用。

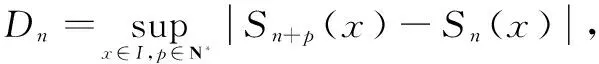
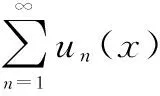
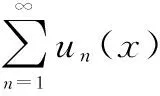
應用定理4，在證明函數項級數非一致收斂時，技術指導路線明確，具有一般性，表述簡便。

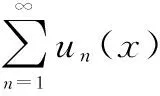
定理3的表述，來源于定理5的思想，定理3的表述方式達到統一完善的理論體系。

2 一些函數項級數非一致收斂的證明方法

證明成立

pxn+p(1-x)α

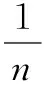
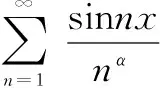
證明事實上成立

Dn≥|Sn+p(x)-Sn(x)|=

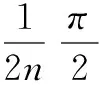
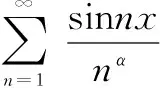
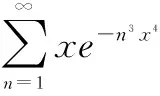
證明成立

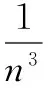
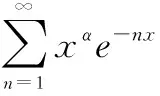
證明成立

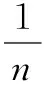
3 含參變量廣義積分一致收斂的柯西準則的改進

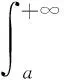
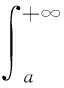
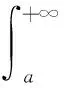
定理7是證明含參變量廣義積分非一致收斂的常用方法，然而應用此方法在證明各個含參變量廣義積分非一致收斂時都要重復的敘述一遍，表述有些繁瑣。可以將定理5結果的表述形式給予改進，使其方向性明確，方便于使用。

記

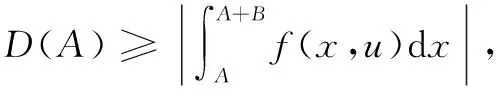
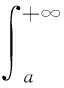
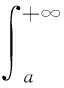
應用定理8，在證明含參變量廣義積分非一致收斂時，技術指導路線明確，具有一般性，表述簡便。

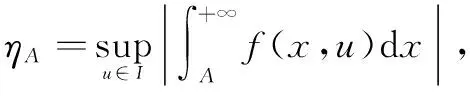
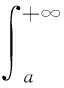
定理8的表述方式來源于定理10的思想，定理8的表述方式達到了與定理10統一完善的理論體系。

4 一些含參變量廣義積分非一致收斂的證明方法

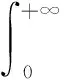
證明由不等式ey≥1+y，(y∈[0,+∞))，得

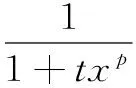
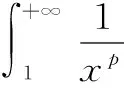
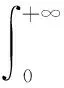
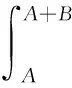
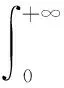
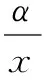
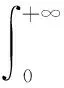
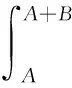
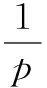
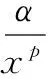
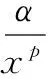
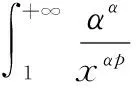
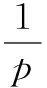
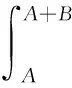
5 一個發散數列的例子

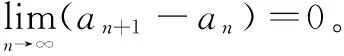
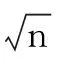
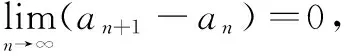
6 結束語

本文通過對函數項級數一致收斂的柯西準則的表述形式給予改進，找到了判別函數列非一致收斂的一般性方法，利用該方法，對各種問題的解決給出了技術指引方向，敘述統一簡便，達到理論完善高度統一，并有利于掌握和傳播。

[1] 黃玉民,李成章.數學分析(下冊)[M].2版.北京:科學出版社,2007.

[2] 華羅庚,著.王元,校.高等數學引論(第二冊)[M].北京:科學出版社,2009.

[3] 裴禮文.數學分析中的典型問題與方法[M].北京:高等教育出版社,2002.

[4] 常庚哲,史濟懷.數學分析教程(下冊)[M].北京:高等教育出版社,2003.

[5] 陳紀修,於崇華,金路.數學分析(下冊)[M].2版.北京:高等教育出版社,2003.

[6] 菲赫金哥爾茨.微積分學教程(第二卷)[M].8版.北京:高等教育出版社,2006.

[7] 卓里奇.數學分析(第二卷)[M].4版.北京:高等教育出版社,2006.

[8] 匡繼昌.實分析與泛函分析(續論)(上冊)[M].北京:高等教育出版社,2015.

[9] 白玉蘭,陳述濤.一個二次廣義積分的順序交換問題[J].哈爾濱師范大學自然科學學報,1987,3(3):13-18.

[10] 匡繼昌.Dirichlet積分九種解法的思路分析[J].高等數學研究,2012,15(4):61-64.

[11] 邢家省,楊小遠,白璐.兩無窮區間上積分交換次序充分條件的改進及其應用[J].四川理工學院學報:自然科學版,2016,29(1):87-92.

[12] 邢家省,楊小遠.廣義菲涅爾積分的積分交換次序計算方法[J].四川理工學院學報:自然科學版,2016,29(3):85-92.

[13] 邢家省,楊小遠,白璐.菲涅爾積分計算中的一致收斂性的證明方法[J].吉首大學學報:自然科學版,2016,37(5):1-9.

[14] 邢家省,楊義川,王擁軍.菲涅爾積分的幾種計算方法[J].四川理工學院學報:自然科學版,2016,29(5):88-96.

[15] 邢家省,楊義川,王擁軍.函數列的廣義積分的極限定理及其應用[J].吉首大學學報:自然科學版,2016,37(6):1-9.

[16] 趙香蘭.幾種判別函數項級數非一致收斂的方法[J].大同職業技術學院學報,2003,17(4):50-62.

[17] 王慶東,王路橋.一種判定函數列非一致收斂的方法[J].高師理科學刊,2016,36(9):12-14.

[18] 王慶東.一種判定含參變量無窮限反常積分非一致收斂的方法[J].高師理科學刊,2016,36(1):15-19.

[19] 邢家省,楊義川,王擁軍.函數列的黎曼積分的極限定理及其應用[J].四川理工學院學報:自然科學版,2017,30(3):73-78.

TheModifiedFormofSeriesofFunctionsviaCauchyCriterionofUniformlyConvergence

XINGJiasheng1,2,YANGYichuan1,2

(1.School of Mathematics, Beihang University, Beijing 100191，China;2.LMIB of the Ministry of Education, Beihang University, Beijing 100191，China)

Considering the discrimination of uniform convergence of the Series of functions and generalized integrals with parametric variables, Cauchy criterion discrimination is an effective method to prove series with function terms and improper integral with variable which is uniformly convergent, but for non-uniform convergence, Cauchy criterion is fairly cumbersome to apply. So a general method for the non-uniform convergence of the function term series is improved and the generalized integrals with parametric variables is given. This improvement is easier to apply and master through a large number of examples.

series of functions; generalized integral of parametric variable; uniformly convergence; Cauchy criterion; non-uniform convergence

O177.2

A

2017-07-20

國家自然科學基金項目(11271040)；北京航空航天大學校級重大教改項目(201403)

邢家省(1964-)，男，河南泌陽人，副教授，博士，主要從事偏微分方程、微分幾何、泛函分析方面的研究，(E-mail)xjsh@buaa.edu.cn;

楊義川(1970-)，男，甘肅天水人，教授，博士，主要從事邏輯代數、序代數、軟計算及其應用方面的研究，(E-mail)ycyang@buaa.edu.cn

1673-1549(2017)05-0074-05

10.11863/j.suse.2017.05.13