基于二次逼近神經網絡的反應釜預測控制

,,

(合肥工業大學 電氣自動化工程學院，合肥 230009)

基于二次逼近神經網絡的反應釜預測控制

林勇,宋一凡,溫陽東

(合肥工業大學電氣自動化工程學院，合肥230009)

針對在化工生產過程中使用連續攪拌反應釜(Continuous Stirred Tank Reactor，CSTR)時存在的控制方式不便，調節的精確度不高等問題;在對實際問題進行分析建模的基礎上，提出了一種基于二次逼近神經網絡模型的預測控制方法;該方法首先利用多層前饋神經網絡模型去逼近連續攪拌反應釜系統的多步預測值，其次在已創建的預測模型的基礎上優化并求解預測控制的二次目標函數，以得到最優的控制參數，最后由通過泰勒展開式的二次逼近得到非線性預測控制器的最優解;通過對控制模型的模擬以及帶入相關參數進行仿真實驗，對連續攪拌反應釜控制系統的仿真結果進行分析表明：該方法控制精確度較高，并且是可行有效的，能夠使生產效率得到顯著提高且保證了產品的質量，具有較高的實用價值。

連續攪拌反應釜；神經網絡；廣義預測控制；泰勒展開；二次逼近

0 引言

反應釜是現代化工生產中必不可少的主要設備之一。反應釜[1]有兩種工作方式：連續生產和間歇生產。前者被稱作連續攪拌反應釜(continuous stirred tank reactor,簡稱CSTR)。CSTR如今已成為工業上最常用的反應釜，它有許多優點：既能進行勻相反應,又可進行多相反應；其次它的攪拌機制使得反應釜中反應物料的濃度均勻；此外，CSTR投資少、生產出的產品質量穩定、熱交換能力強，有很高的生產效率。但在實際生產中多數化工廠仍然使用人工和常規PID方法對CSTR進行控制，調節反應釜的生產過程參數如溫度、流量、濃度、反應速率等，從而得到符合工藝要求的生成物產品。由于CSTR系統本身的強非線性，導致傳統的控制方法難以符合生產要求，參數控制不夠精確，達不到預期的控制效果，對化工產品的質量和產量都有很大影響，故對CSTR控制方法的改進就顯得尤為迫切。在分析了CSTR系統的特點和生產控制要求之后，筆者提出了基于二次逼近神經網絡的預測控制方法，通過神經網絡辨識CSTR這個強非線性系統，然后通過對廣義控制律的泰勒展開，實現了對生產參數值的二次逼近，改善了控制精度和控制效果，提高了生產效率和產品質量，很好地滿足了化工廠生產要求。

1 CSTR的基本結構和原理

CSTR的基本結構如圖1所示。其基本結構由攪拌容器和攪拌機兩大部分組成。其中，攪拌容器包括內構件、筒體和換熱元件。攪拌機包括攪拌軸、攪拌器及其密封和傳動裝置等。

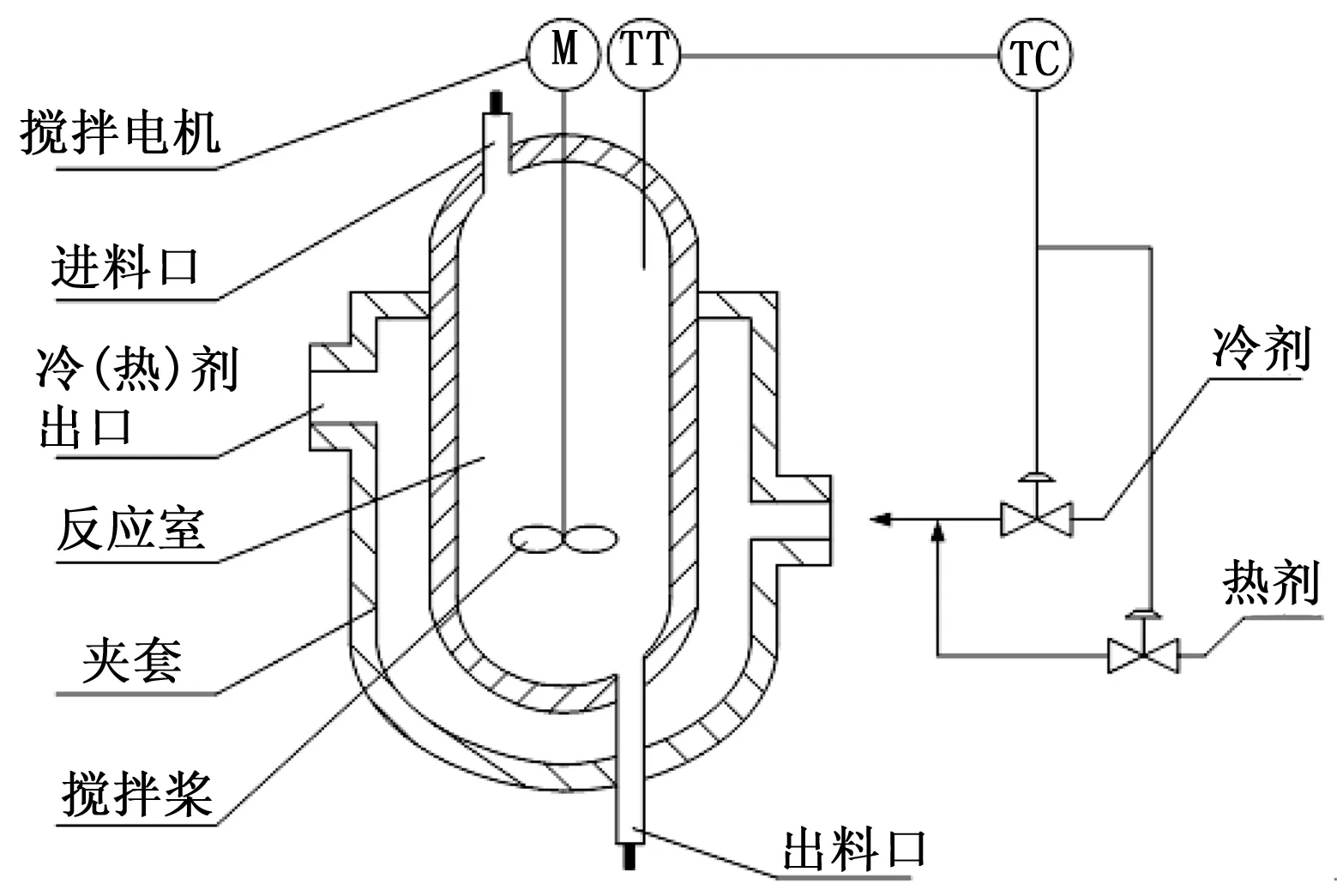
圖1 CSTR基本結構

反應釜中的化工生產是個復雜的過程。在進行化工生產時，首先向反應釜中投入物料以及催化劑，然后通過攪拌使反應釜內物料均勻進行化學反應。升溫階段在反應釜的夾套中通以一定的高壓蒸汽，當反應釜內的溫度上升到設定值時，控制蒸汽的速度使溫度保持恒定，確保反應在最佳工況下正常進行。反應完成后便是降溫過程，通以冷卻介質使反應釜溫度降低，結束整個反應過程。恒溫階段對整個生產過程而言最為關鍵，偏高或偏低的溫度值都會影響化工反應進行的深度和轉化率，從而影響產品的質量。由于此類化工生產為放熱反應，為了確保反應釜溫度穩定在設定值，通過在夾套中通以一定的冷卻介質，來吸收多余熱量，使反應釜的溫度符合工藝要求[2]。

由此可見，冷卻劑流量的大小，直接影響著反應釜溫度，從而影響化工產品的生產，故本文通過控制冷卻劑流量的大小，使反應釜恒溫反應階段溫度穩定在設定值，從而間接地控制生成物的濃度，得到質量合格的產品。

2 預測控制

模型預測控制[3](簡稱預測控制)是產生于工業過程控制領域的一類新型計算機控制算法。發展至今預測控制在理論和實踐兩個方面都取得了豐碩的成果。實際生產過程中的系統往往強耦合、強非線性，還具有時滯時變等特性。傳統的預測控制在面對這種復雜的控制對象和更高的控制要求時，很難實現實時有效的控制，達不到預期的控制精度和效果。所以對于非線性系統的預測控制優化研究，使其具有更好的控制效果和更大的應用范圍已成為近年來的熱點課題之一。

人工神經網絡，不僅具有自學習、自適應不確定性系統的動態特性，而且理論上可以逼近任意復雜非線性系統。神經網絡的這些特點和自身優勢，為解決非線性問題提供了一種新的思路。因此將神經網絡[4]和預測控制結合起來，在傳統預測控制的基礎上運用神經網絡方法進行優化，得到基于神經網絡的非線性預測控制[5]來彌補傳統預測控制在面對強耦合，強非線性時變系統時的不足，更好的解決非線性系統控制問題。

基于上述理論，本文通過結合神經網絡和預測模型的思想，設計了基于神經網絡的預測模型，有效辨識了CSTR這個強非線性系統，解決了傳統控制中存在的問題，實現對CSTR的有效控制。

3 廣義預測控制理論

在預測控制理論中需要構建一個預測模型，該模型能夠根據系統的歷史數據和未來的輸入，預測系統未來的輸出值從而描述系統動態行為，對系統進行預測控制。通常GPC(廣義預測控制)[6]采用CARIMA(Controlled Auto-Regressive Integrated Moving Average)“受控自回歸積分滑動平均模型”作為預測模型，這個模型可以寫成：

A(z-1)y(k)=B(z-1)u(k-1)+C(z-1)ξ(k)/Δ

(1)

式中u(k)和y(k)分別是過程的輸入和輸出，ζ(k)是零均值噪聲序列，A(z-1)、B(z-1)和C(z-1)則分別是后移算子z-1的多項式：

A(z-1)=a0+a1z-1+...+anaz-na

B(z-1)=b0+b1z-1+...+bnbz-nb

C(z-1)=c0+c1z-1+...+ancz-nc

使用CARIMA模型有以下好處：1)該模型能描述一類非平穩擾動；2)可保證系統輸出穩態誤差為零。

通常將廣義預測控制器[7]所基于的目標函數定義為如下的控制增量形式：

(2)

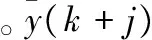
(3)

本文用一組神經網絡模型去逼近一個非線性系統的多步預測值，再優化求解預測控制的二次目標函數，與傳統方法不同的是，該方法并未使用遞推Diophantine方程來求解控制量，從而減少了計算量且提高了預測精度，具體過程如下文中所述。

4 基于二次逼近神經網絡的非線性預測控制器

4.1 多步預測模型的神經網絡組

對于最一般形式的單輸入單輸出的離散非線性系統，可以由下面的輸入/輸出模型來描述[8]：

y(k)=f(y(k-1),...,y(k-n),

u(k-1),...,u(k-m-1))

(4)

上述非線性系統的輸出量y(k)的第j步預測值由當前信息x0(k)和未來j時刻內的控制增量ΔUj(k)共同決定。

y(k+j|k)=fj(x0(k),ΔUj(k))j=1,2,...,N

(5)

其中：x0(k)=[y(k),...,y(k-n+1),u(k-1),...,u(k-m+1)]T，ΔUj(k)=[Δu(k),...,Δu(k+j-1)]T

然后用一組三層前饋神經網絡去逼近預測模型(5)

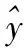
1,2,...,N

(6)

這一共是N個網絡，Wj為第j個網絡的權值向量。第j個網絡的結構如圖2所示。

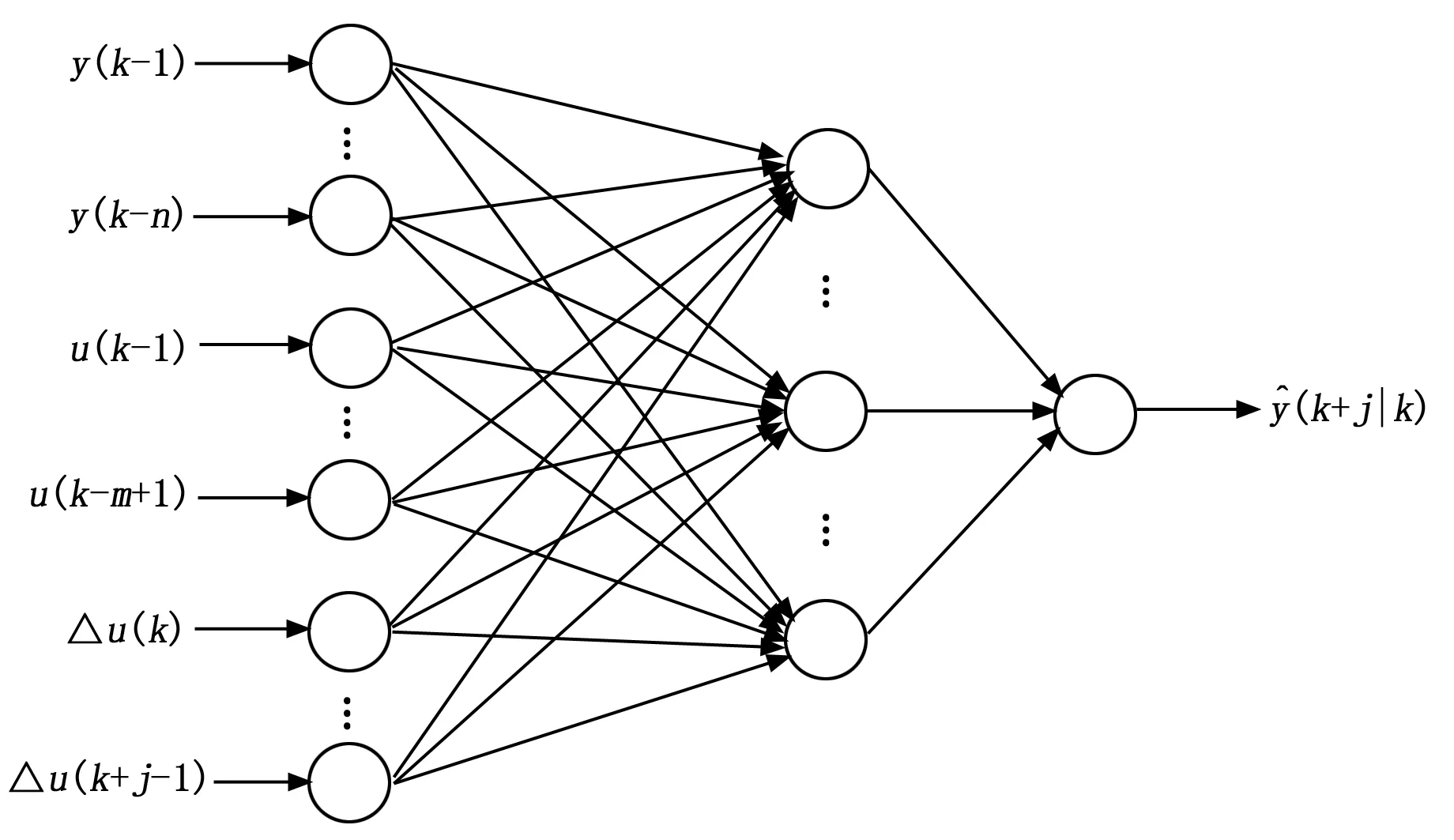
圖2 多預測模型網絡組中的第j個網絡結構示意圖

定義：

(7)

用非線性最小二乘法遞推算法對Wj進行在線學習。

4.2 二次逼近預測控制律

本系統的控制律仍然以式(2)為目標函數，對式(6)應用一階泰勒展開，可以得到：

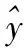
(8)

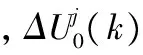
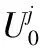
(9)

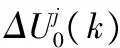
(10)

假設當j>Nu時，Δu(k+j-1)=0，所以定義

(11)

于是對

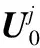
(12)

定義

(13)

由式(8)、(12)和(13)得

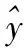
(14)

將其寫成向量形式

式中，

將目標函數(6)也寫成向量形式：

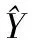
(15)

將式(14)代入式(15)后得到:

(16)

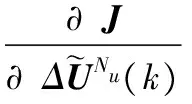
(17)

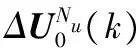
(18)

由(18)可推導出當前時刻基于二次優化目標逼近的控制增量序列

(19)

4.3 CSTR預測控制

在實際化工生產中連續攪拌反應釜動力學模型可用2個非線性[9]微分方程描述:

(20)

k3qc[1-e-k2/(qc)](Tc-T)

(21)

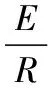
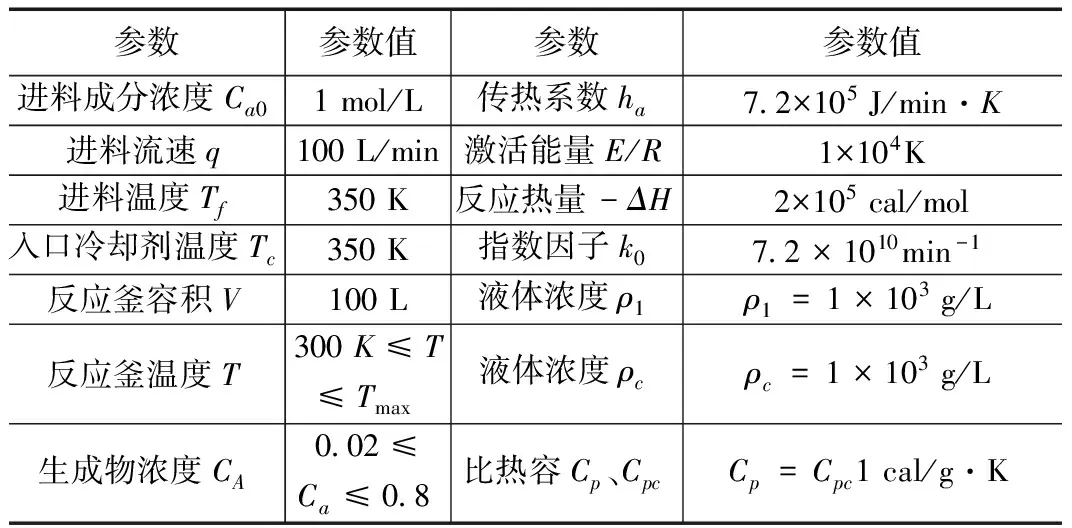
表1 CSTR參數表

由表1數據計算得到k1=1.44×103g/L，k2=6.987×102，k3=0.01。

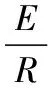
net=newff(pr,[5,1],‘losig’,‘losig’},‘trainlm’,‘learngdm’);

net.trainParam.epochs=1000;

net.trainParam.goal=0.001;

net.trainParam.show=10;

net.trainParam.lr=0.05;

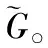
CSTR系統的控制目標是通過控制qc使反應釜的溫度T穩定在設定值，得到符合工藝的生成物濃度CA來生產質量合格的產品。例如某次生產工作點Ca=0.5 mol,T=350 K,TC=300 K，溫度T的設定值為350 K，系統的約束條件為：

(22)

U={TC∈R|200≤TC≤370}

則系統的狀態量和控制量轉化為：

(23)

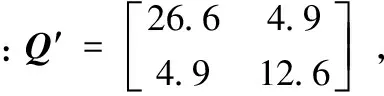
5 仿真驗證與分析

本文采用Matlab軟件作為仿真工具。廣義預測控制參數取預測長度N1=3,加權系數λ=0.35，控制長度Nu=2，柔化系數α=0.5。利用一組在(80，115)間的隨機幅值序列作為激勵輸入CSTR機理模型，以周期為0.1 s的間隔采樣得到樣本數為600的一組輸入輸出數據，取前400組用于模型的辨識，后200組數據分別作為訓練集和驗證集，通過控制qc使反應釜的溫度T穩定在設定值，得到符合工藝的生成物濃度CA從而生產質量合格的產品。

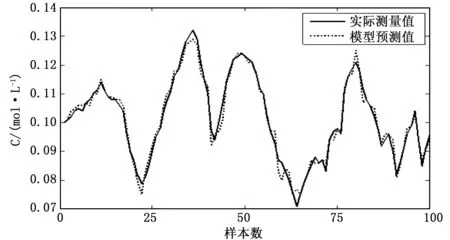
圖3 濃度CA的實際測量值和神經網絡預測模型預測值對比

經模型辨識后，為了檢驗神經網絡預測模型的辨識效果，取100份樣本數據進行神經網絡預測效果測試，圖3為100份樣本生成物濃度

C

A

實際測量值和神經網絡預測模型預測值的對比，經計算得實際測量值和神經網絡預測模型預測值平均誤差為1.42%，表明所得模型辨識精度較高，預測效果較好。

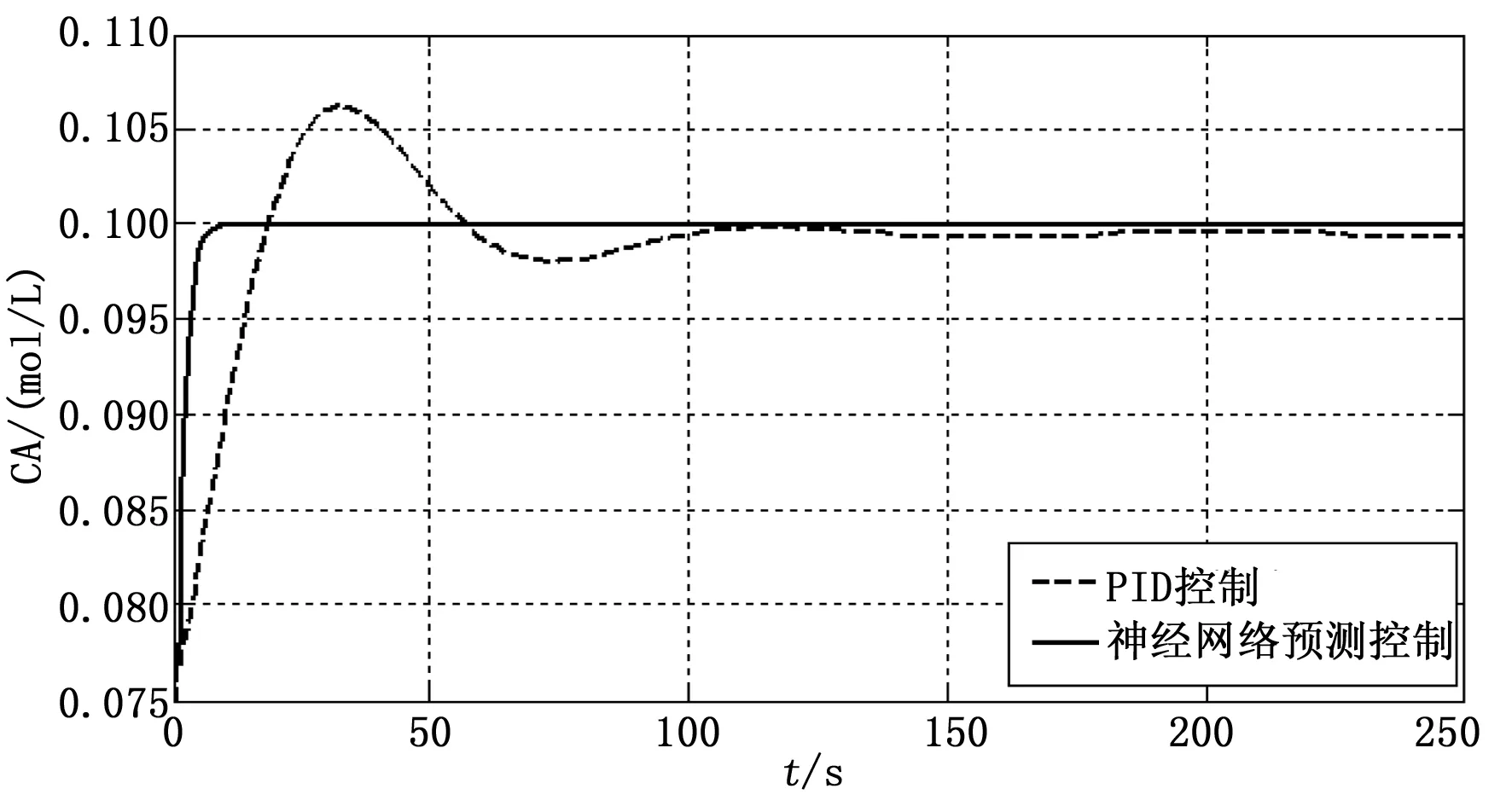
圖4 神經網絡預測控制和常規PID控制效果對比

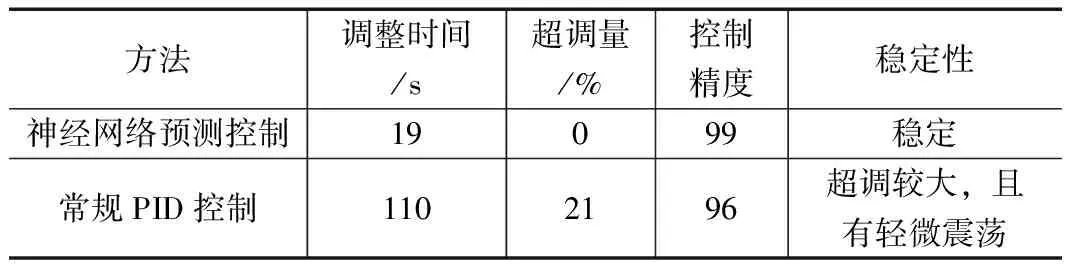
方法調整時間/s超調量/%控制精度穩定性神經網絡預測控制19099穩定常規PID控制1102196超調較大，且有輕微震蕩

由表2數據對比分析可知，神經網絡預測控制相比于常規PID控制，調整時間較短，滿足生產的快速性要求；神經網絡預測控制控制精度為99%，高于常規PID的96%，滿足生產的控制精度要求，保證產品質量；神經網絡預測控制無超調，常規PID控制有超調且伴有輕微震蕩現象，滿足生產的穩定性要求。綜上，本文提出的神經網絡預測控制效果優于常規PID控制，是一個較好的CSTR控制方法。

6 結論

基于二次逼近神經網絡預測控制方法，通過神經網絡模型很好的辨識了CSTR這個強非線性系統，其次通過廣義控制律的泰勒展開實現了對生產參數值的二次逼近提高了預測控制性能。優于常規PID控制，提高了CSTR系統的控制精度和控制效果，提高了生產效率且保證了產品的質量，具有較高的應用價值，也為預測控制的優化發展提供借鑒意義。

[1]楊軍民. 反應釜溫度控制的研究現狀及化工自動化發展現狀[J].廣東化工，2010,37(5)：288-290.

[2]于海英. 化學反應釜溫度模糊控制器[D].阜新:遼寧工程技術大學,2002.

[3]馬海軍，王文中，翟素蘭，等.基于卷積神經網絡的監控視頻人,數統計算法[J].安徽大學學報(自然科學版)2016，40(3)22-28.

[4]王華強，石亞娟，王健波.神經網絡模糊PID在水輪機調速中的應 用[J].合肥工業大學學報(自然科學版),2012,35(9):1187-1191.

[5]譚元飛.基于神經網絡預測控制的鍋爐過熱汽溫控制研究[D].西安:西安科技大學，2012.

[6]張 興,戴 瑩,李 爭.一種時變非線性對象神經網絡PID控制的仿真[J]. 合肥工業大學學報(自然科學版),2006,29(11):1375-1379.

[7]Neshasteriz A R, Khaki S A, Sadjadian H. Generalized predictive control and tuning of industrial processes with second order plus dead time models[J]. Journal of Process Control, 2010(20).

[8]程 輝,秦 廷,陳宗海.液位對象的一種非線性廣義預測控制策略研究[J].計算機仿真,2006, 23(9): 333-335.

[9]滿 紅,邵 誠.基于Hammerstein-Wiener模型的連續攪拌反應釜神經網絡預測控制[J].化工學報,2011, 62(8): 2275-2276.

[10]曾誼暉，龔金科，李金梅，楊賢平.數控切削加工表面粗糙度RBF神經網絡預測模型[J].煤礦機械，2011，32(3)：117-119.

[11] 李奇安，褚 健.對角CARIMA模型多變量廣義預測控制改進算法[J].控制理論與運用，2007，24(3)： 423-427

[12] 陳 薇.非線性預測控制算法的研究與應用[D].合肥：中國科學技術大學，2007.

PredictiveControlofReactorBasedonQuadraticApproximationNeuralNetwork

Lin Yong，Song Yifan，Wen Yangdong

(School of Electric Engineering and Automation , Hefei University of Technology , Hefei 230009 , China)

A predictive control method based on neural network is presented for the problem of production inconvenience and low precision in a continuous stirred tank reactor(CSTR) which is widely used in chemical process. Firstly, using a multi-layer feed forward neural network to approximate the CSTR system’s multi-step predictive value, secondly based on the forecast model for solving quadratic objective function optimization predictive control by the Taylor expansion approximation quadratic nonlinear predictive control law controller. The simulation results of CSTR show that : that essay’s method has high accuracy and that method is feasible and effective. The utility model has the advantages of high production efficiency, high product quality and high practical value.

continuous stirred tank reactor(CSTR); neural network; generalized predictive control; Taylor expansion; quadratic approximation

2017-04-04；

2017-04-19。

林 勇(1978-)，男，安徽合肥人，副研究員，碩士生導師，主要從事自動控制、計算機控制方向的研究。

溫陽東(1955-)，男，安徽合肥人，教授，主要從事自動控制、計算機控制、現場總線技術應用方向的研究。

1671-4598(2017)10-0081-04

10.16526/j.cnki.11-4762/tp.2017.10.022

TP273

A