基于逼近的動態面二階滑模的船舶航向跟蹤控制

張 凱，李鐵山，趙 蓉

(大連海事大學 航海學院，遼寧 大連 116026)

基于逼近的動態面二階滑模的船舶航向跟蹤控制

張 凱，李鐵山，趙 蓉

(大連海事大學 航海學院，遼寧 大連 116026)

針對船舶航向非線性運動數學模型存在不確定性誤差的情況下，提出一種新穎的動態面二階滑模智能控制方法。首先采用動態面控制（DSC）技術,以消除傳統Backstepping方法中存在的“計算爆炸”問題。為了削弱滑模控制中固有的抖振效應，提高系統的魯棒性，引用了一種新穎的二階滑模控制方法。然后直接利用徑向基神經網絡技術逼近模型誤差，同時采用最少學習參數（MLP）技術，以減少控制器的計算負擔，所設計的控制器可以保證閉環系統中所有信號一致最終有界，并使跟蹤誤差任意小，最后通過仿真驗證所提算法的有效性。

船舶航向控制；動態面控制（DSC）；二階滑模控制；徑向基神經網絡；最少學習參數（MLP）

本文針對船舶航向運動非線性數學模型，設計了一種基于徑向基神經網絡逼近的動態面二階滑模控制器，用徑向基神經網絡（RBFNN）逼近模型誤差，并把二階滑模控制方法與動態面控制方法相結合，對控制器進行設計。所設計的控制器，保證了船舶航向控制系統中所有信號一致最終有界，并使得跟蹤誤差任意小。最后，利用Matlab的Simulink仿真工具進行仿真研究，仿真結果驗證了所提算法的有效性，并且具有良好的魯棒性。

1 問題的描述

船舶航向控制非線性數學模型中，舵角δ和航向φ的關系可以描述為：

其中：K，T分別為時間增益和時間常數，是船舶前進速度和船長的函數；?為模型誤差；˙為首搖角速度。為一個非線性函數，可以近似表示為：

式中：e1和e2為船舶非線性系數，是實值常數。

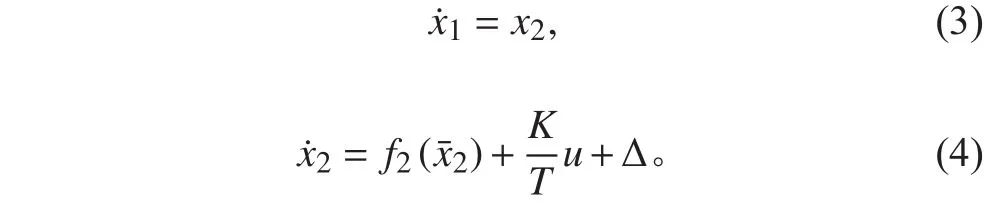
假設：參考信號xd光滑有界且具有二階連續有界的導數，即存在一個常數D0＞0，使得集合成立。

2 控制器設計

針對船舶航向控制的非線性數學模型系統設計一種基于反演法的動態面二階滑模控制器，使閉環系統的所有信號一致最終有界，且使跟蹤誤差能夠任意小。下面給出簡要的控制器設計過程。

定義第1個誤差面

選取李雅普諾夫候選函數

定義濾波器誤差

定義第2個誤差面

則

將式（11）代入到式（6）得

考慮到位置跟蹤、虛擬控制和濾波誤差，選取李雅普諾夫候選函數

設計的控制器由2部分組成

取

其中p＞0，k＞0，c2＞0根據連續函數分離技術可知

則選擇最終控制器

3 穩定性分析

再次選取李雅普諾夫候選函數

將式（15）、式（20）、式（21）、式（22）代入式（24），并選擇

得

因為p＞0，k＞0，所以

選取自適應律

注意到

則

注意到

則

由式（31）可得到

4 計算機仿真

以大連海事大學遠洋教學實習船“育龍”輪為例進行仿真研究，以驗證所提控制算法的有效性。

“育龍”輪的參數為：船長126.0 m，船寬20.8 m，滿載吃水8.0 m，方形系數0.681，船速7.7 m/s。通過計算得船舶運動非線性數學模型參數K=0.478，T=216，e1=1，e2=30。

在仿真中，選取控制器設計參數c1=8，c2=15，τ=0.01，r2=0.5，Γ2=1，σ2=1，利用Matlab進行計算機仿真研究，其結果如圖1～圖3所示，從圖1可知，船舶具有較快的響應速度和較好的跟蹤能力，能夠實現滿意的控制效果。從圖2可知，舵角在反向達到滿舵之后，慢慢的趨近于0，最終鎮定到0。圖3為自適應律曲線。

圖1 船舶航向歷時曲線Fig.1 Time response of ship course

圖2 舵角歷時曲線Fig.2 Time response of rudder angle

5 結 語

本文在考慮建模不確定性的情況下，針對船舶運動非線性數學模型，采用動態面二階滑模控制技術和最小學習參數技術，提出了一種新穎的控制方法，在增強了系統魯棒性的同時，還減少了控制器的計算負擔。計算機仿真結果表明了所提算法的有效性。

圖3 自適應律歷時曲線Fig.3 Time response of

[1]王林,陳楠,高嵬.基于 Backstepping 的船舶航向自適應滑模控制[J].船電技術,2012,32(4):16–18.

[2]DU Jia-lu,CHEN Guo.Nonlinear adaptive ship course tracking control based on backstepping and nussbaum gain[C]// IEEE Proceeding of Control Conference 2004,Boston,America.2004:6–7.

[3]卜仁祥,劉正江,李鐵山.迭代滑模增量反饋及在船舶航向控制中的應用[J].哈爾濱工程大學學報,2007,28(3):268–272.

[4]GAO X R,HONG B G,XING S W,et al.Designed slide mode controller for ship autopilot with steering gear saturation[C]//14th International Conference on Algorithms and Architectures for Parallel Processing,2014,Dalian,China.2014:386–395.

[5]WU X,GAO S,ZHU Q D,et al.Design of ship course control system based on backstepping sliding mode[J].Control Engineering of China,2009,16:52–55.

[6]LEVANT A.Sliding order and sliding ac-curacy in sliding mode control [J].Interna-tional Journal of Control,1993,58(6):1247–1263.

[7]LEVANT A.Higher-order sliding modes differentiation and output-feedback control[J].International Journal of Control,2003,76(9–10):924–941.

[8]苗保彬,李鐵山,羅偉林.基于DSC和MLP的船舶航向跟蹤控制[J].大連海事大學學報,2015,39(4):5–8.

Dynamic surface second order sliding mode control based on approximation for course-keeping control of ship

ZHANG Kai,LI Tie-shan,ZHAO Rong
(Dalian Maritime University,Navigational College,Dalian 116026,China)

In this paper,a novel dynamic surface second order sliding model control method is proposed for coursekeeping control of ship in the presence of uncertain errors.The controller is constructed by “dynamic surface control” technique to solve the problems of “explosion of complexity” in the traditional Lyapunov stability theory.A novel second order sliding model control method is proposed in this paper,which is not only capable of strengthening robustness of the system,but also attenuating inherent chattering of classical sliding mode control method effectively.And then the radial basis function neural network approximation technique is used for approximating modeling errors,meanwhile the “minimum learning parameter” technique is used to reduce the computational burden of the algorithm.The controller guarantees that all the close-loop signals are uniform ultimate bounded (UUB) and that the tracking er-rors converge to a small neighborhood of the desired trajectory.Finally,simulation results are given to illustrate the effectiveness of the proposed algorithm.

ship course control；dynamic surface control (DSC)；second order sliding mode control；radial basis function neural network (RBENN)；minimum learning parameter (MLP)

V249.122

A

1672 – 7649(2017)10 – 0066 – 04

10.3404/j.issn.1672 – 7649.2017.10.012

0 引 言

船舶航向控制是船舶運動控制的基本內容，它直接影響著船舶的操縱性、安全性和經濟性。然而由于船舶具有大慣性、大時滯、非線性等特點，其運動極易受到風、浪、流等強干擾的影響，船速及裝載的變化也會造成船舶模型的參數攝動，加之環境參數的嚴重干擾及測量的不精確性等都使船舶動態產生明顯的不確定性[1 – 2]。長期以來，人們一直致力于不確定性非線性系統的魯棒及自適應控制研究，特別對于存在不確定性干擾的復雜未知系統[3]。由于算法簡單，傳統的滑模控制方法已經被成功地應用到了船舶航向控制中[4 – 5]，但是傳統滑模控制中的不連續切換特性會導致抖振現象的出現，這不僅降低了系統的控制精度，使系統的控制性能變差，甚至會嚴重損壞控制元件。為削弱傳統滑模控制中的抖振現象，Levant等[6 – 7]提出一種新型的二階滑模控制算法。近年來，針對系統的建模不確定性影響，苗保彬等[8]提出一種新穎的船舶航向跟蹤控制方法。

2016 – 09 – 17；

2016 – 10 – 19

國家自然科學基金資助項目(51179019,61374114)；遼寧省教育廳重點實驗室基礎項資助項目(LZ2015006)；中央高校基本科研業務費資助項目(3132016313)

張凱(1993 – )，男，碩士研究生，研究方向為船舶運動控制、水下機器人控制算法。