最小二乘法擬合熱電阻測溫結果的準確性分析
李曉麟
最小二乘法擬合熱電阻測溫結果的準確性分析
李曉麟
(甘肅省計量研究院,甘肅 蘭州 730070)
工業上已經對鉑、銅等金屬熱電阻進行電阻和溫度特性的研究。針對工業上對提高熱電阻測溫準確性的測量方法,本文采用最小二乘法對數據進行處理,總結出一種測電阻和溫度關系的轉化公式和精度表。然后,比對其他方法測出的數據得出,本方法可以提高溫度傳感器對溫度測量的準確性。
溫度測量;熱電阻;最小二乘法;準確性
在工業生產和生活中,溫度是一個很重要的測量物理量,若要精確測量還需要克服一些問題。就目前應用比較多的溫度傳感器而言,主要包括4種:熱電偶、熱電阻、熱敏電阻和集成溫度傳感器。熱電阻溫度傳感器作為比較廣泛應用的測溫元件之一,具有互換性好、耐腐蝕、性能穩定以及使用方便等特點[1]。工業上的做法經常是將熱電阻接到電橋的電橋臂上,通過測量,電橋兩端輸出的不同的電流,轉化為溫度的不同值,從而知曉測得的溫度。在實際使用過程中,大多數是按照廠商提供的溫度標準值,如果需要測量精度高的溫度,就需要與計量機構出具的證書對比修正,或者按照規程上的要求進行系數校正[2]。當然,測量的時候有時只能對有限的溫度測量范圍進行修改校正,沒有被修正的測量溫度點就會產生較大的測量誤差。工業上的常規方法是由于鉑電阻的非線性以及電橋臂的測量溫度不平衡帶來了一定的測量誤差,通常把鉑電阻放在測溫的現場,減小測溫點到測量變換電路之間的距離,這樣就會減小產生的自身引線電阻[3]。本文以pt100鉑電阻傳感器為例,通過測量更寬的測量溫度點,對數據進行最小二乘法分析校正,得出最小誤差的測量溫度值,從而提高精度。
1 測量熱電阻的原理以及進行溫度測量的誤差
金屬鉑具有一種固有特性,即電阻值隨溫度的增加而增加,我們可利用這一特點來測量溫度。在某一特定溫度下,通過測量鉑電阻的電阻,然后通過計算公式得到需要的溫度值。科研工作者和工程師們按照國際統一的標準來制造很多具有代表性的工藝產品,然后進行各方面的測試,并對所得的數據進行分析處理,得到相應的曲線圖,總結得到一個具有普遍性意義的公式(即電阻與溫度特性的公式):

式中,RT代表溫度為T時鉑電阻的電阻值,R0代表溫度為0時的鉑電阻的電阻值,A、B、C代表常數。
由JJG229-2011《工業鉑銅熱電阻檢測規定》可知,鉑電阻的檢測溫度范圍為0~100℃,通過國家規定的標準來檢測合格的鉑電阻傳感器的測量溫度的檢定點,由查分度表得到。其中分度表是理想情況下純鉑的電阻與溫度的關系表。當式(1)(2)中R0=100.000 0,A=3.908 4×10-3,B=-5.775 44×10-7,C=-4.183 45×10-12時,其電阻和溫度的關系可以用分度表來表示。但是,在工業生產過程中,廠家生產出來的鉑電阻的電阻-溫度特性關系與分度表上有一定的偏差,這是由以下幾點原因造成的:①鉑絲的純度;②鉑敏感元器件絕緣;③材料熱膨脹和電泄露。
2 提高熱電阻測溫精度和減小誤差的方法
鉑電阻是一種典型的熱電阻溫度傳感器,直接用它比對分度表來測量溫度,這樣的方法會產生較大的測量誤差,即使是準確度最高的鉑電阻(AA級)也會有0.1左右的測量溫度偏差,尤其是對一些精密溫度測量時有非常大的影響。分析鉑電阻的電阻與溫度的特性公式得出,要測定公式中的系數,對于溫度大于0的時候要測量三點;對于溫度低于0的時候要測量4個點。令0℃附近的點為T1、下限溫度為T2和上限溫度為T3,測得實際的電阻值為R1、R2、R3,得出以下公式[4]:
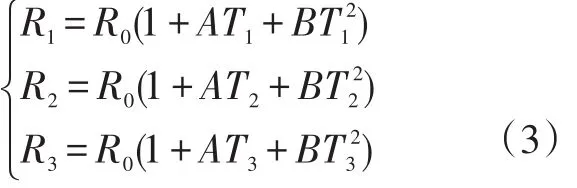
從而求出未知數R0,A和B,這樣對測量點測量時可以得到準確的溫度數據。
3 以最小二乘法進行擬合
使用最小二乘法求擬合曲線,不同的數學模型模擬出來的函數不一樣,當要擬合的函數為多項式時,假設給定的一組數據( )xiyj,i,j=1,2,…,N求P(P<N)次多項式

即有方程組:
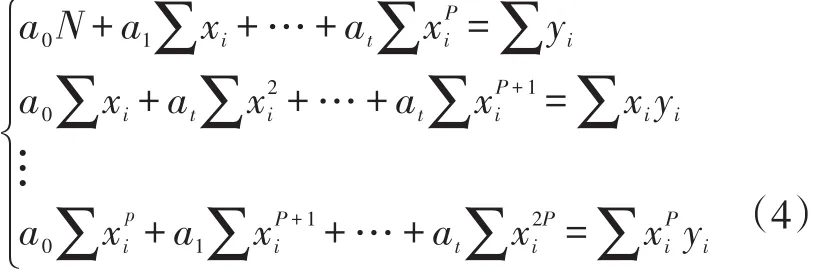
利用此方程證明有唯一的解,這個方程適合一般的數據擬合,但此方程存在一定的缺點,當P足夠大的時候,此方程就失效了。
在溫度大于0的電阻和溫度特性的公式中,只需要測量3個溫度點(比如溫度為0附近時的某溫度點T1、溫度可以達到的上限點T2、溫度可以達到的下限點T3),再加上這3個點所處位置的電阻值R1、R2、R3,就可以得到R0、A、B的值(通過最小二乘法計算得到)。其中里面的系數由以下方程組得到:
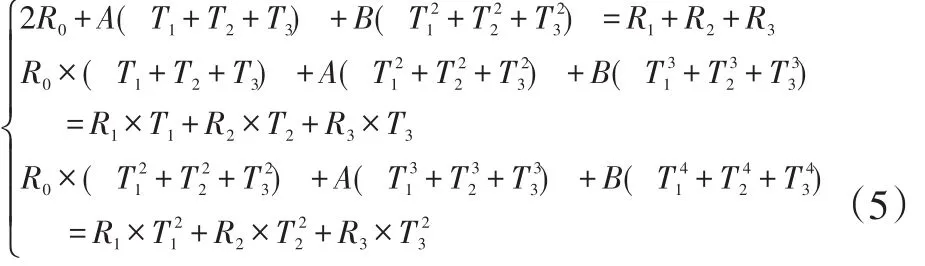
再由上式得到的系數值算出被測鉑電阻的分度表。
4 驗證最小二乘法擬合數據的準確性
在求近似函數的所有數值方法中,有一種叫做函數逼近,即曲線擬合。曲線擬合只是要求給定的數據點在某種程度上逼近或者某種意義上講是一種基本的趨勢,但不要求擬合的數據在每一個節點上與函數值一模一樣。我們經常會選擇合理的數值方法對數據進行篩選和處理,數據擬合受到大多數人的青睞。考慮到誤差,進行曲線擬合處理數據時,往往很難選取合適的函數來擬合這些曲線,于是就產生了最小二乘法。
與傳統方法比較來驗證最小二乘法的正確性和可靠性,用工業上的鉑電阻來測試,測量數據見表1。

表1 鉑電阻測量數據結果
5 結語
本文通過最小二乘法原理,利用一些基本公式求出鉑電阻中電阻與溫度特性里面的一些參數,得出的數據與分度表進行比較,來確定是否準確。在實際生產生活中,使用新函數擬合出來的測量溫度的數據比之前的要準確很多,也可以用來提高熱電阻的準確度。
[1]國防科工委科技與質量司.熱學計量[M].北京:原子能出版社,2002.
[2]國家質量監督檢驗檢疫總局.JJG229-2010工業鉑銅熱電阻檢定規程[S].北京:中國質檢出版社,2010.
[3]國防科工委科技與質量司.計量技術基礎[M].北京:原子能出版社,2002.
[4]王能超.計算方法[M].武漢:華中科技大學出版社,2010.
Accuracy Analysis of Measuring Thermal Resistance Temperature by Least Square Method
Li Xiaolin
(Gansu Institute of Metrology,Lanzhou Gansu 730070)
The resistance and temperature characteristics of platinum,copper and other metal thermal resistors have been studied in industry.In order to improve the accuracy of temperature measurement by thermal resistance in industry,this paperused the least square method to process the data and sum up a transformation formula and an accuracy table for measuring the resistance and temperature.Then,compared with other methods,this method can improve the accuracy of temperature measurement by the temperature sensor.
temperature measurement;thermal resistance;least square method;accuracy
TH811
A
1003-5168(2017)09-0053-02
2017-08-02
李曉麟(1988-),男,碩士,工程師,研究方向:熱工計量。

