考慮負載率均衡及風險成本的變電站規劃

王思瑩 常 俊 李 永 趙殿平 李 磊

?

考慮負載率均衡及風險成本的變電站規劃

王思瑩1常 俊2李 永3趙殿平1李 磊1

（1. 東北電力大學電氣工程學院，吉林吉林 132012; 2. 國網沈陽供電公司，沈陽 110000;3. 國網河南民權縣供電公司，河南民權 476800）

負載率均衡和風險成本是對變電站規劃結果在實際應用中適應性的直接反應。建立了變電站規劃數學模型，提出了考慮負載率均衡和風險成本的變電站規劃方法。該方法將負載率均衡用熵值來處理，在風險理論的基礎上，建立設備、變電站及線路風險成本模型，同時反應了規劃結果的經濟性和合理性，結合K-means算法對該模型進行有效求解。算例分析驗證了所提規劃方法的合理性與傳統規劃方法相比，采用所提方法規劃結果更加合理。

變電站規劃；負載率均衡；風險成本；熵值；K-means算法

配電網變電站作為電力系統的重要一環，是連接不同電壓等級的樞紐點，其規劃的合理性直接影響著系統的網絡結構、供電可靠性及運行經濟性。

文獻[1-3]分析了不利地形、行政區域等實際因素對配電網變電站選址、定容及供電區域規劃結果的影響，建立了相應的變電站規劃模型。文獻[4]從供電能力的角度對配電網變電站進行了規劃。文獻[5]在傳統配電網變電站規劃模型的基礎上，考慮了變電站本身運行產生的損耗費用、故障產生的停電損失費用，并利用混沌遷移知識的差分文化算法實現對模型的求解。文獻[6-8]不僅討論了初始建設成本，同時考慮了其運行維護成本、廢棄成本等，即利用全壽命周期理論（LCC）對配電網變電站的規劃進行建模。文獻[9-11]將負荷、電價和土地價格的不確定性作為風險成本，建立基于LCC理論的經濟性最優的配電網變電站規劃模型。

目前在配電網變電站規劃課題研究中，多為對于外在環境對規劃結果的影響，如地理因素、不確定性等，針對變電站規劃時設備及線路本身的故障風險討論不足。對此，本文基于熵理論，通過對各變電站負載率分析反應負荷分布均衡程度，將設備風險、變電站風險及線路風險分別予以量化并轉為經濟性指標，結合兩者建立了考慮負載率均衡和風險成本的變電站規劃模型，使得方案在滿足經濟性與可靠性的同時更符合實際情況，最終利用K-means算法實現對該模型進行有效求解。

1 變電站規劃模型的建立

1.1 基于熵理論的負載率均衡評估

在進行變電站規劃時，一般以規劃區域負荷預測結果、負荷類型、現有變電站構成情況及容載比要求作為根據，通常忽略了對各變電站負載率的要求，使得負荷在各變電站上分配不均，變電站出現重載或輕載的現象。由于負荷的地理分布在規劃前就已確定，故可以通過規劃變電站位置及供電范圍，解決變電站負載率不均衡的問題。在不超過變電站容量、滿足負荷需要的情況下，盡可能使變電站的負載率均衡，避免變電站出現重載或輕載的情況，提升配電網供電能力。

信息熵是對事物不確定性的量化，其數值的大小即反應事物不確定性的大小。在評估變電站負載率指標時，指標離散程度越小，其分布的信息熵越小，也就是說，信息熵可以作為負載率分布均衡度的量度[12-13]。

以單個變電站負載率e占系統所有變電站負載率和的大小表征變電站的重要度I，有

根據熵理論，構建變電站負載率熵，即

由上式可知，當變電站負載率相等時，熵值達到最小，即min=1/ln。其中為變電站總座數。

1.2 建立風險成本模型

在工程應用中，國內外學者普遍接收的風險定義是：“風險是指人類從事某種活動時，在一定時期內可能會發生的具有損失性后果事件的危害，這種危害來自于兩個方面，即可能性（概率）和嚴重性（后果），而風險值就是二者的乘積，即=×”[14-15]。

為建立經濟性最優的變電站規劃模型，本文從停電損失角度對變電站規劃風險進行評估。由于停電損失與變電站容量、負荷類型、停電發生和持續時間等因素有關，建立風險成本評估模型如下：

式中，為風險成本；為失效事件發生的概率；為故障的經濟后果嚴重度指標。

1）設備風險成本

（1）元件失效發生的概率P

（2）故障的經濟后果嚴重度S

首先，需統計在不同停電持續時間時，系統處于最大負荷下的總停電損失，將得到的總停電損失與總最大負荷做商，得到平均用戶停電損失模型，即各類用戶停電損失函數SCDF()。本文通過經驗，取SCDF()見表1[17]，可得到各類用戶停電損失和停電持續時間的關系。

表1 各類用戶停電損失

當各故障的持續時間在表中無直接對應的時間時，其停電損失可由表1中相鄰的故障時間的線性插值計算得到。

其次，在建立的SCDF()基礎上，結合各類用戶的用電量比例和負荷率，可以能得到說明綜合停電損失和停電時間的關系的綜合停電損失函數CCDF()，即

式中，為第類負荷；為用戶的類別數；c為第類用戶的用電量比例，SCDF()為第類用戶的停電損失函數，L為第類用戶的負荷率。

最后，結合設備所帶負荷大小S建立故障的經濟后果嚴重度模型，即

由上述可得設備風險成本為

2）變電站風險成本

假設斷路器、熔斷器、隔離開關100%可靠，即不考慮其故障率，當變壓器發生故障時，若此變電站無備用容量或另一臺變壓器容量不夠，所切負荷的停電時間等于變電站的修復時間，則修復時間可由變電站的修復率求得。

變電站故障的經濟后果嚴重度S=CCDF()×S，S為該變壓器所帶所有負荷。

變壓器風險成本指標R=P×S。

3）線路風險成本

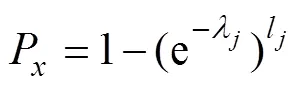
線路故障的經濟后果嚴重度為

S=fCCDF()×S（7）

式中，S為該線路所帶所有負荷。

線路風險成本

R=P×SFj（8）

所有線路風險成本

1.3 建立變電站規劃模型

式中，substation為變電站投資及運行費用；line饋線投資費用和年網損費用之和；為網損折算系數；W為線路所帶有功負荷，(S)為變電站的負載率；l為第座變電站到第個負荷的距離，為變電站負載率熵，cos為第座變電站功率因數。

需要說明的是，在進行實際變電站規劃時，應首先由負荷的大小、位置及類型分別選取適當的變電站容量，然后在得到變電站容量的基礎上根據該區域的容載比確定變電站個數，最后，根據本文所建立的變電站規劃模型確定變電站的位置和供區范圍。當變電站容量選取出現多個備選方案時，可分情況討論每種容量方案下利用本模型確定的規劃結果，再對比不同情況下的規劃結果，以經濟性最優確定最終規劃方案。

2 基于K-means算法的模型求解

2.1 K-means算法基本原理

K-means算法是基于劃分的聚類算法，這類算法將數據集歸為不同簇內，各簇間相似度低且互不相交，各簇內相似度較高。

其基本思想是：首先將數據集歸為個不同簇，且人為或任意選擇各簇中的一個對象作為該簇中心點；在建立準則函數的基礎上，為達到最大程度降低函數值的目的，對各簇中的數據進行重新分配，并更新此時各簇的中心點；重復以上步驟直至各簇中心點不再變化為止。需要注意的是，在迭代過程中，進行數據重新分配時，應遵循距離就近原則，將數據對象分配給最近的那個中心點所在的簇，從而使得準則函數的值逐漸減小，實現快速收斂[18]。

K-means準則函數為

2.2 初始聚類中心的選擇

為加快收斂速度得到較好的規劃結果，本文利用最大最小距離法確定初始聚類中心。首先，根據數據對象情況設定一密度參數，將數據實際分布情況與該參數進行對比，可以得到一高密度區域，其中的數據對象構成一高密度點集合。其次，對中所有數據對象進行分析，取處于最高密度的數據對象作為第1個聚類中心1，在此基礎上，取距離1最遠的另一個高密度點作為第2個聚類中心2。

為求取第3個聚類中心，定義中數據對象X到1、2的距離為(X,1)和(X,2)，在本文中，即為兩數據對象在地理位置上的距離。將滿足max(min((X,1)), min((i,2)))的數據對象作為3，以此類推,找到個初始聚類中心。

2.3 應用

對變電站規劃來說，規劃區域之前可能已經存在部分變電站，此時，確實初始聚類中心時，先選擇已建成變電站作為初始聚類中心（1～），其他（）個初始聚類中心利用最大最小距離法進行選擇，同時，在進行聚類時，（1～）聚類中心位置不變，即聚類位置不更新，一直為初始聚類中心。其他聚類中心位置不斷更新。

在本文中，以變電站規劃費用作為準則函數。求解基本流程如圖1所示。

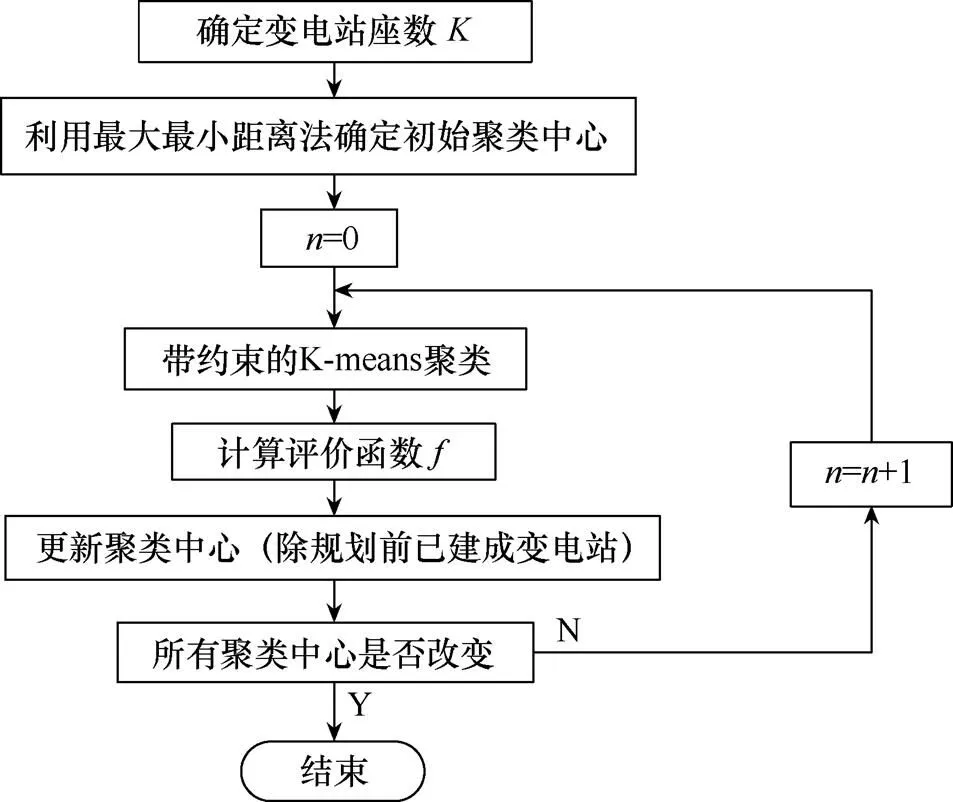
圖1 變電站規劃K-means算法流程圖

3 算例分析

本文引用文獻[1]算例對前文建立的模型進行驗證。規劃區域負荷分布如圖2所示。

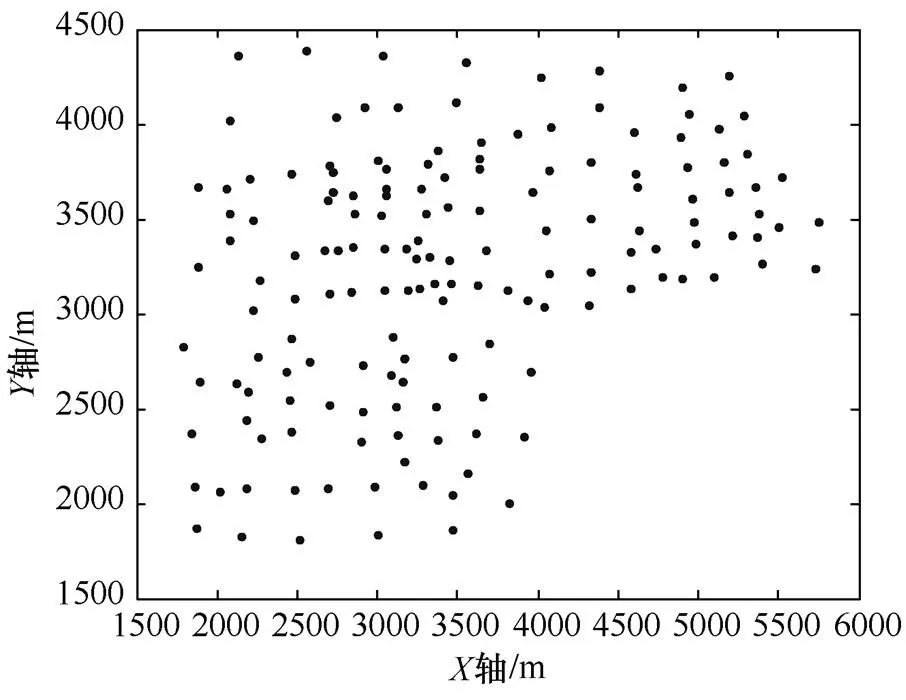
圖2 規劃區域負荷分布

若規劃區域選取2×50MVA作為變電站的容量，則該地區需要4座變電站，是否考慮負載率均衡的規劃結果分別如圖3、圖4所示。

在不考慮負載率均衡的情況下，計算得到變電站成本為4672.8萬元，其中風險成本為893.3萬元，各變電站負載率見表2，負載率熵為0.7868。

圖3 未考慮負載率均衡的變電站規劃方案

表2 未考慮負載率均衡的變電站規劃結果

圖4 考慮負載率均衡的變電站規劃方案

在考慮負載率均衡的情況下，計算得到變電站成本為4535.7萬元，其中風險成本為926.5萬元，各變電站負載率見表3，負載率熵為0.6723。

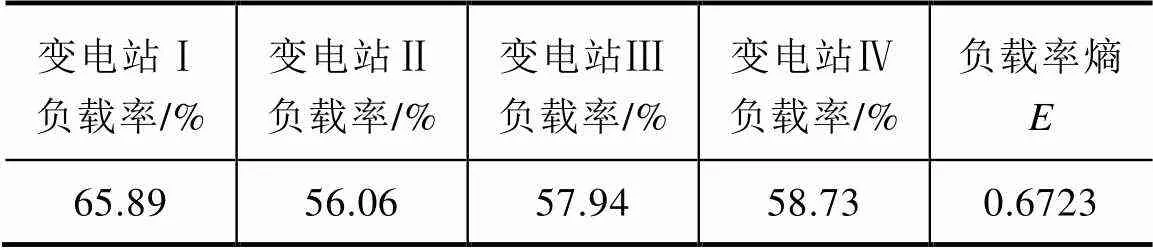
表3 考慮負載率均衡的變電站規劃結果

對比圖3和圖4并結合表2和表3可知，考慮負載率均衡進行變電站規劃時，所得最優規劃方案風險成本較未考慮負載率均衡進行變電站規劃所得的最優規劃成本有所增加，但由于負載率熵有較大幅度的下降，使得最終計算所得變電站規劃成本有所降低，即圖4所示規劃方案優于圖3所示規劃方案方案。

4 結論

本文建立了考慮負載率均衡和風險成本的變電站優化規劃的數學模型，并利用K-means算法對模型進行求解。規劃模型不僅包括變電站和線路的投資和運行費用，還計及了設備風險成本、變電站風險成績線路風險成本，將負載率均衡度以熵的形式引入成本模型中。由前文可以得出，考慮負載率均衡的變電站規劃方案風險成本比不考慮負載率均衡的情況略高，但是從實際運行角度來看，規劃結果更加合理，負荷分布更均勻，不會出現變電站重載或輕載的現象，符合實際需求。利用本文提出的變電站規劃方法可以對配電網變電站進行合理的規劃，滿足工程需求，為后續的配電網規劃工作打下基礎。

目前分布式電源在配電網中的滲透率越來越高，研究其對配電網變電站規劃的影響也變得十分必要，涉及潮流多向流動以及優化目標更為復雜，將作為后續主要研究內容。

[1] 符楊, 衛春峰, 李振坤, 等. 考慮地理信息和行政邊界的變電站供區優化[J]. 電網技術, 2014, 38(1): 3728-3733.

[2] 陶青松, 肖峻, 王笑一. 基于地理信息的變電站選址定容模型與算法[J]. 電力系統及其自動化學報, 2010, 22(6): 32-37.

[3] 王成山, 魏海洋, 肖峻, 等. 變電站選址定容兩階段優化規劃方法[J]. 電力系統自動化, 2005, 29(4): 62-66.

[4] 于明, 郭華, 潘珍, 等. 基于提升供電能力的配電網協調規劃探析[J]. 電氣技術, 2015, 16(10): 107-110.

[5] 汪臻, 盛四清, 周慶捷. 不確定環境下配電網變電站選址定容[J]. 電力建設, 2014, 35(3): 59-63.

[6] 蘇海鋒, 張建華, 梁志瑞, 等. 基于全壽命周期成本的配電網變電站選址定容優化規劃[J]. 電力系統自動化, 2012, 36(23): 59-64.

[7] 蘇海鋒, 張建華, 梁志瑞, 等. 基于GIS空間分析與改進粒子群算法的變電站全壽命周期成本規劃[J]. 中國電機工程學報, 2012, 32(16): 92-99.

[8] 蘇海鋒, 張建華, 梁志瑞, 等. 基于改進均值聚類隨機粒子群算法的變電站LCC規劃[J]. 電工技術學報, 2012, 27(4): 209-215.

[9] 姜小靜, 蘇海鋒, 梁志瑞. 計及風險成本的配電網變電站規劃方法[J]. 電力自動化設備, 2014, 34(6): 141-145, 167.

[10] 閆麗梅, 許愛華, 任爽, 等. 一種變電站選址的新方法[J]. 高電壓技術, 2007, 33(9): 75-79.

[11] 何永秀, 羅濤, 方銳. 基于風險分析的變電站選址優化研究[J]. 華北電力大學學報, 2011, 38(3): 53-57, 66.

[12] 張炳達, 王靜. 基于熵原理的電能質量評估新方法[J]. 電力自動化設備, 2009, 29(10): 35-38.

[13] 丁明, 過羿, 張晶晶, 等. 基于效用風險熵權模糊綜合評判的復雜電網節點脆弱性評估[J]. 電工技術學報, 2015, 30(3): 214-223.

[14] (加)李文沅, 周家啟[等]譯. 電力系統風險評估模型、方法和應用[M]. 北京: 科學出版社, 2006.

[15] 劉秋華, 董丹丹, 韓韜. 基于層次分析法的配電網風險評估指標體系研究[J]. 電氣技術, 2016, 17(9): 39-42.

[16] 王璁, 李曉, 屠幼萍. 變壓器質量風險的全壽命周期評估方法研究[J]. 電氣技術, 2014, 15(5): 31-34, 43.

[17]周莉梅, 范明天. 城市電網用戶停電損失估算及評價方法研究[J]. 中國電力, 2006, 39(7): 70-73.

[18] 苑津莎, 張利偉, 李中, 等. 基于互補免疫算法的變壓器故障診斷[J]. 電工技術學報, 2015, 30(24): 67-75.

Distribution Substation Planning Considering Balance of Load Rate and Risk Cost

Wang Siying1Chang Jun2Li Yong3Zhao Dianping1Li Lei1

(1. School of Electrical Engineering, Northeast Electric Power University, Jilin, Jilin 132012;2. State Grid Shenyang Power Supply Company, Shenyang 110000;3. State Grid Minquan Power Supply Company, Minquan, He’nan 476800)

Balance of load rate and risk cost are direct responses to the adaptability of substation planning results in practical applications. The mathematical model of substation planning is established, and the substation planning method considering load balancing and risk cost is put forward. Based on the risk theory, this paper establishes the cost model of equipment, substation and line, and reflects the economics and rationality of the planning result. The K-Means algorithm is used to analyze the model. The result of the case shows that the rationality of the proposed method is more reasonable than that of the traditional planning method.

substation planning; balance of load rate; risk cost; entropy; K-means algorithm

王思瑩（1992-），女，河北保定人，碩士研究生，主要研究方向為配電網規劃及風險評估。