基于時間序列分析的人體摔倒過程預測

中國船舶重工集團公司第七一三研究所 潘文濤

基于時間序列分析的人體摔倒過程預測

中國船舶重工集團公司第七一三研究所 潘文濤

可穿戴式下肢助行機器人的穩定恢復性能對平衡能力較弱的穿戴者安全性至關重要。針對大干擾下的穩定恢復控制應用，對人體摔倒過程中的動力學及足底壓力變化特征進行分析，通過計算足底壓力中心點（CoP）與足底有效支撐區域多邊形邊界的距離，從而可以實現對人體的穩定性的定量描述。通過自回歸(AR)時間序列模型、最小二乘法(LS)、AIC準則函數等相關理論，建立摔倒過程穩定裕度的時間序列預測模型，實現對人體摔倒過程的預測識別，為摔倒過程的穩定恢復控制策略研究提供依據。

助力機器人；摔倒過程；零力矩點；時間序列

引言

隨著人口老齡化問題的加深，可穿戴式助力機器人在助老行走中具有很大的應用前景[1]。下肢助行機器人行走時，理想情況下可通過控制機器人快速跟隨穿戴者運動，為穿戴者提供助力。然而，在穿戴者有摔倒的趨勢時，助力機器人采取快速跟隨的控制策略，會加速穿戴者的摔倒過程，加重對穿戴者造成的傷害。提前預測穿戴者的摔倒趨勢，并采取相應的控制策略，協助穿戴者重新處于穩定狀態，可避免摔倒對人機系統造成損傷，在摔倒趨勢無法逆轉時，可控制機器人采取相對安全的摔倒姿勢，從而給予穿戴者一定的保護。本文針對大干擾下助行機器人的穩定恢復控制的需求，深入研究人體摔倒預測算法。

在外骨骼下肢助行機器人系統中，穩定性控制方法大部分都是基于ZMP理論，根據穿戴者或者機器人的關節角度、角速度以及加速度信息，計算實際的ZMP位置，再基于ZMP理論實現穩定控制[2]。這些方法存在一定的局限性，首先，基于ZMP穩定性控制方法，機器人的足底必須水平著地，這與人在行走過程中的特點相違背。其次，根據實際運動數據計算ZMP位置，是基于動力學模型，需要精確的參數，對于不同體型的穿戴者來說適應性受限。再有，這些方法是對當前時刻的穩定性進行分析，實時性很難保證，很難滿足安全性需求。在穿戴者處于摔倒趨勢時，如果提前能夠預測識別出摔倒趨勢，根據識別結果采取相應的控制策略，能夠彌補目前穩定性控制方法的不足。

目前，許多學者采用加速度傳感器、角速度傳感器監測人體運動過程，選取合適的傳感器測量閾值對人體摔倒進行判定，應用于對摔倒后的人體進行監測、定位及報警[3-5]。近年來更多的研究集中于對摔倒行為的預測，防止摔倒的發生。對摔倒進行預測，延長摔倒的籌備時間，是摔倒識別相關方向的發展趨勢。針對輔助下肢健全老人行走應用，現有摔倒識別方法沒有結合考慮摔倒過程的動力學穩定性變化情況，而人體的摔倒行為實際上是一系列變化的過程，在這個變化的過程中，人機系統的穩定性也隨之變化，為了實現該過程的穩定恢復，需要根據摔倒過程中不同穩定程度采取不同的策略。因此，在摔倒預測研究中，除了在識別算法上基于歷史數據建立預測模型外，應該對摔倒過程的穩定性進行分析，采用能直接反應動力學穩定性的方法，對摔倒過程各階段穩定性進行定量的描述，為可穿戴式助力機器人的穩定恢復控制策略研究提供依據。

1 穩定性定量描述

基于摔倒過程穩定恢復控制應用，在對摔倒進行預測時，需要對穩定狀況作定量的研究和分析。零力矩點（ZMP, Zero Moment Point）理論是目前類人機器人常用的穩定性分析方法。ZMP是指地面反力向水平面中某點的等效，合力矩為零的點。一般將ZMP與雙足形成穩定支撐區域多邊形邊界的最短距離定義為穩定裕度，穩定裕度是描述人體運動過程穩定性最直觀有效的指標。

ZMP在一定程度上可以由足底壓力中心點(CoP)等效代替[6]。由于足底壓力檢測相對簡單方便，且足底壓力中心點計算簡便，因此本文采用CoP代替ZMP的方式計算摔倒過程中的穩定裕度。

1.1 足底壓力中心點

人體在運動過程中，CoP的位置處于不斷變化的狀態，平穩狀態下處于小范圍內移動；摔倒過程中CoP會沿著摔倒方向發生快速移動。

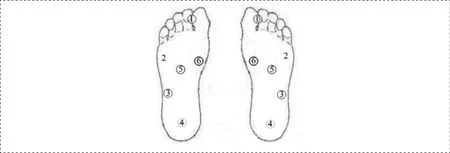
圖1 足底壓測量點

本文根據安裝在足底的壓力傳感器信號，實時計算CoP與支撐各個邊界的最短距離d，從而完成對人體運動中的穩定性狀況進行定量描述。足底壓力測量點位置如圖1中所示。

由式（1）計算出壓力中心點的坐標[XCoP,YCoP,]，其中Fi為壓力傳感器測量值，[xi,yi]為其對應的坐標值。

1.2 雙足支撐多邊形

如圖2所示，人體在正常站立時，由圖2所示的左右腳中的傳感器1、2、3、4構成最大的支撐區域。在穩定裕度的計算中，依據足底壓力的信息計算對應時刻的支撐區域多邊形。

圖2中外圍多邊形即為雙足正常站立時的支撐區域，內部曲線為人體向前摔倒過程中CoP的變化軌跡，從圖2中可以看出在前向摔倒過程中CoP沿摔倒方向與支撐區域邊界的距離逐漸減小。

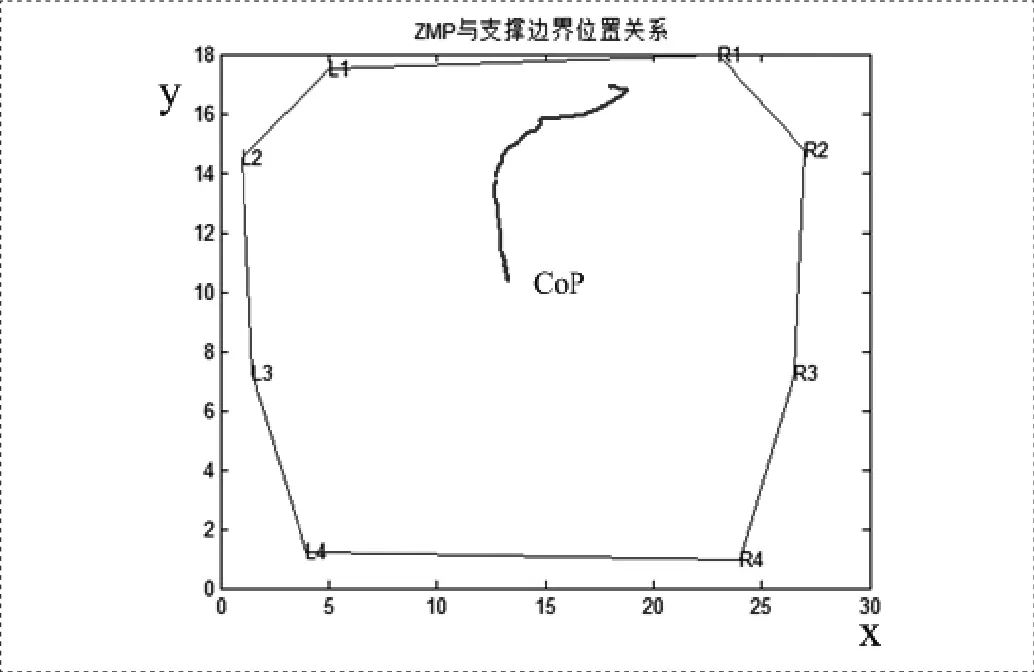
圖2 摔倒過程CoP變化曲線

在計算穩定區域時，根據足底壓力信息，除去足底壓力為零的傳感器，選擇最外部的足底壓力傳感器，并確定其坐標[xi,yi]。將[xi,yi]作為支撐多邊形的頂點，支撐區域多邊形的邊界采用直線方式進行擬合，由式（2）可以確定支撐區域的各個邊界。

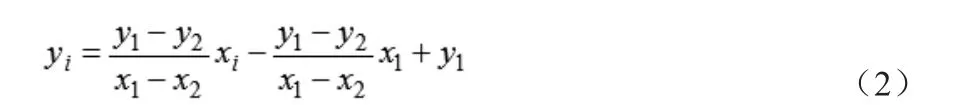
[x1,y1]，[x2,y2]為兩相鄰的足底壓力傳感器的坐標。定義變量：

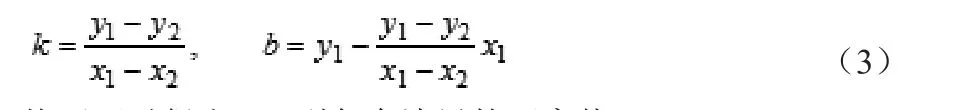
從而可以得出CoP到各個邊界的距離值：

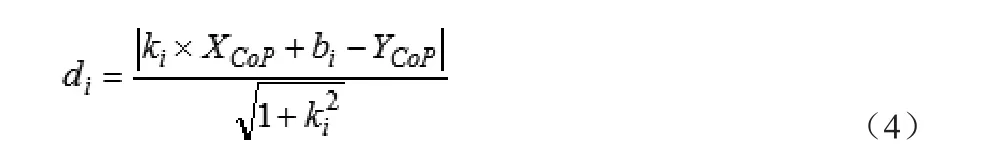
2 摔倒預測算法

摔倒過程中，可以將穩定裕度看作是與時間相關的序列，可以建立合適的時間序列預測模型，通過預測模型對人體的穩定裕度進行多步預測，從而提高系統的響應速度，得到未來時刻人體穩定裕度的狀況，作為助力機器人穩定恢復控制策略的依據。

相鄰時刻的穩定裕度值存在一定的相關性，如圖3中所示，通過過去時刻的穩定裕度值，可以預測未來時刻穩定裕度值。選擇合適的時間序列預測模型，可以實現對摔倒過程的穩定裕度曲線進行快速準確的預測，從而預測出人體的穩定狀態。

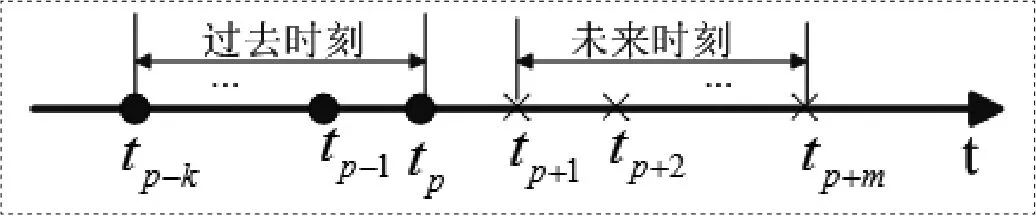
圖3 預測原理示意

2.1 時間序列模型

采用時間序列進行預測時，選取不同的時間序列模型對預測結果的準確性和實時性有非常大的影響。常用的時間序列模型有：自回歸(AR)、移動平均(MA)、自回歸移動平均(ARMA)[7-8]。通過試驗獲取人體摔倒過程足底壓力傳感器數據，從而可以計算人體摔倒過程中穩定裕度的時間序列，計算該序列的自相關、偏相關系數，依據經驗和現有理論可以選擇最優的時間序列模型。各中時間序列模型所對應的自相關、偏相關系數特征如表1中所示：

表1 時間序列模型階次

圖4、圖5分別為根據某次摔倒試驗所計算的穩定裕度時間序列的自相關以及偏相關系數。

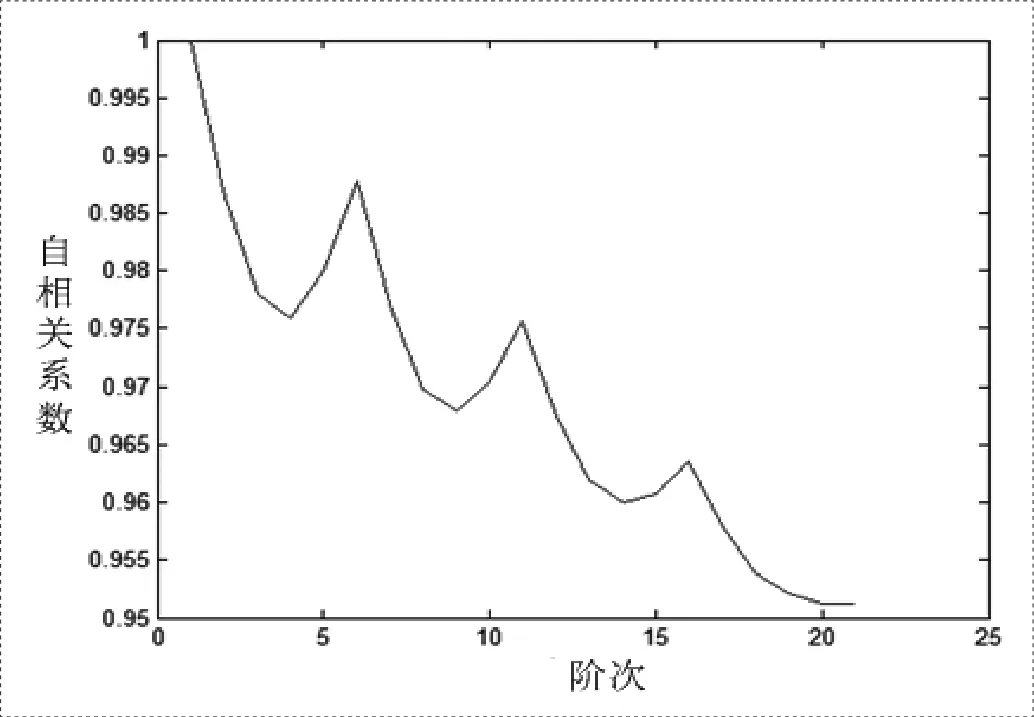
圖4 穩定裕度曲線的自相關系數

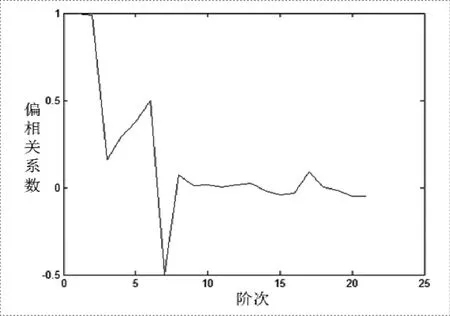
圖5 穩定裕度曲線的偏相關系數

從上圖中可以看出人體在摔倒過程中穩定裕度的時間序列的自相關系數呈拖尾性，偏相關系數呈現截尾性，符合典型的AR時間序列模型特征，因此本文選擇AR模型作為人體摔倒過程的預測模型。

AR(p)時間序列模型滿足式（5）～式（7）的條件：

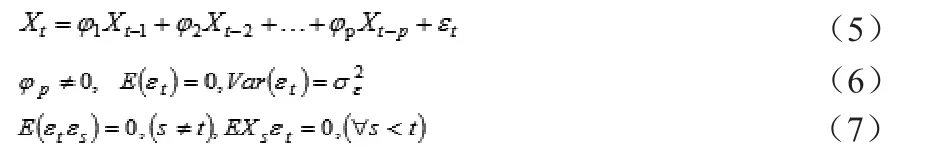
對于AR（p）時間序列模型來說，Xt僅與Xt-1，Xt-2，…，Xt-p有線性關系，在Xt，Xt-1，Xt-2，…，Xt-p已經確定的情況下，Xt與其它時刻觀測值無關，εt是一個均值為零的白噪聲，僅對Xt有影響。

2.2 模型定階

AIC準則即最佳準則函數法是目前最常用的時間序列模型定階方法。AIC準則是采用準則函數對預測模型和原始數據的擬合程度，以及模型中待定參數的個數進行描述。AIC準則函數的一般形式為：N為樣本個數，為時間序列殘差，P時間序列待定參數個數。

由圖4、圖5可知，AR(p)時間序列模型階次不大于10。采用人體摔倒過程的穩定裕度訓練數據計算AR時間序列模型各階次的AIC函數值。實際計算可知，AR模型的AIC函數在6階之后AIC函數不再減小，因此，采用AR(6)模型對穩定裕度時間序列進行預測。

2.3 模型參數辨識

確定時間序列模型參數是時間序列分析的一個最重要的環節，模型參數的選擇直接影響到預測誤差的大小和預測速度。最小二乘法是系統辨識理論中參數估計的最經典方法。最小二乘法進行參數估具有先驗知識少、計算量小、收斂性能好，算法簡單等優點。

對于AR（p）模型未來時刻的值y(t)可以由以下公式計算獲得，y(t — p)為p時刻前的觀測值，ε(t)為均值為零的白噪聲[14]。

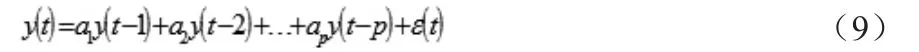
定義向量：

則AR(p)模型的殘差可以表示為：

最小二乘法參數估計的原理就是尋求θ的估計值，使其極小化殘差的平方和：

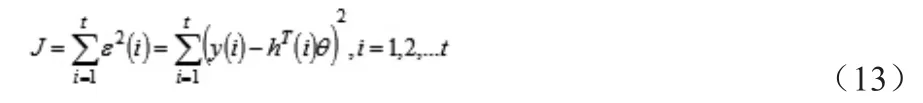
定義向量：

殘差的平方和可以表示為：

由上式可以確定θ的估計值：

使得殘差的平方和J最小，θ的估計值即為最優的AR(P)時間序列模型的參數。

2.4 預測流程

時間序列預測算法流程如圖6中所示。首先選定訓練數據，采用最小二乘法和AIC判別準則取定最優的時間序列模型階次和參數，再由得到的預測模型測試數據進行預測。

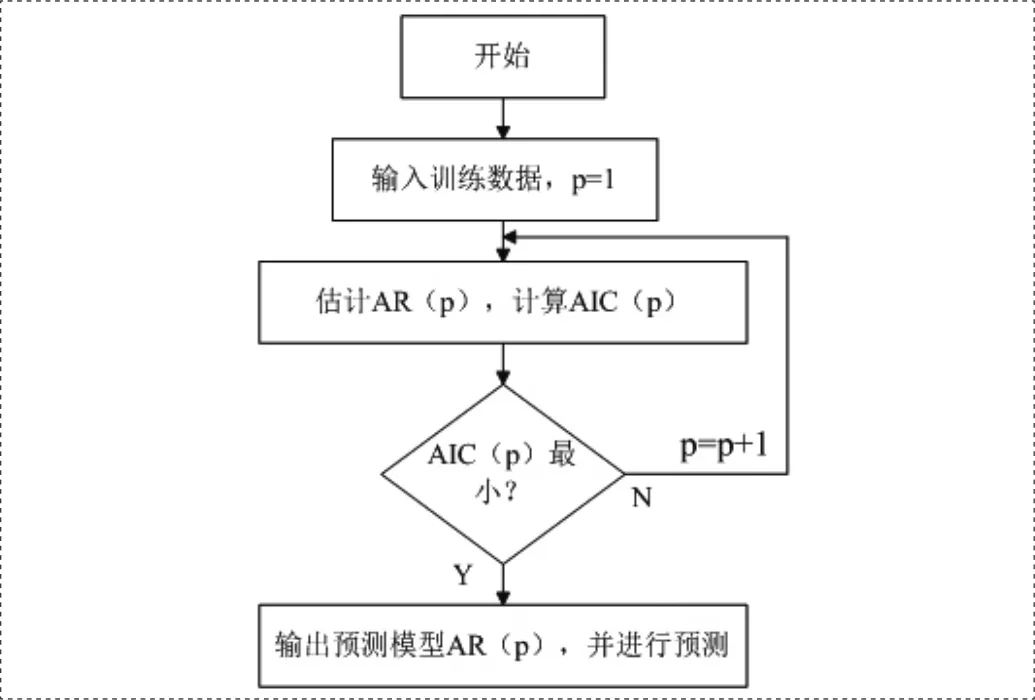
圖6 預測程序流程圖

3 試驗與結果分析

足底壓力信號采集采用貼片式壓力傳感器，安裝在鞋墊底部，具有輕便、精確、不影響人體運動狀態的特點。

人體摔倒過程時間短暫，對人體摔倒過程的分析需要有較高的數據采樣頻率。DSP芯片相對于單片機具有功耗低、運算速度快、運算精度高的優點。足底壓力采集系統由DSP芯片STMS320C2812及附屬電路組成的最小系統構成，實現對雙腳12個足底壓力傳感器的實時數據采集。

本文讓試驗者穿著鞋墊底部裝有多個壓力傳感器的鞋進行多次摔倒試驗。試驗者身高165cm，體重55kg，選取了四個典型的摔倒過程：前向摔倒、后向摔倒、左摔和右摔，每組摔倒過程分別采集60組數據，選取40組摔倒過程信息作為訓練數據，其它作為測試數據，每個完整的摔倒過程足底壓力信息采樣點約為2000個。

本文以前摔過程作為示例，整個摔倒過程足底壓力變化曲線如圖7所示，結合前文所述的穩定性判別方法，可以計算出摔倒過程中的穩定裕度變化曲線，將其視為與摔倒時間相關的一個時間序列。

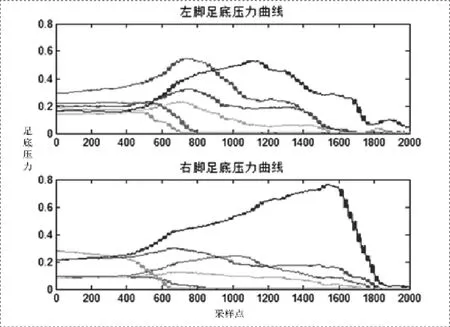
圖7 摔倒過程足底壓力曲線

由最小二乘法計算得到AR(6)時間序列模型的參數如表2中所示：

表2 AR時間序列預測模型參數

由于摔倒過程時間比較短，為了提高頻率響應，對摔倒過程的穩定裕度序列采取多步預測的方法。選取摔倒過程的穩定裕度樣本N為1800，預測步長L為3。

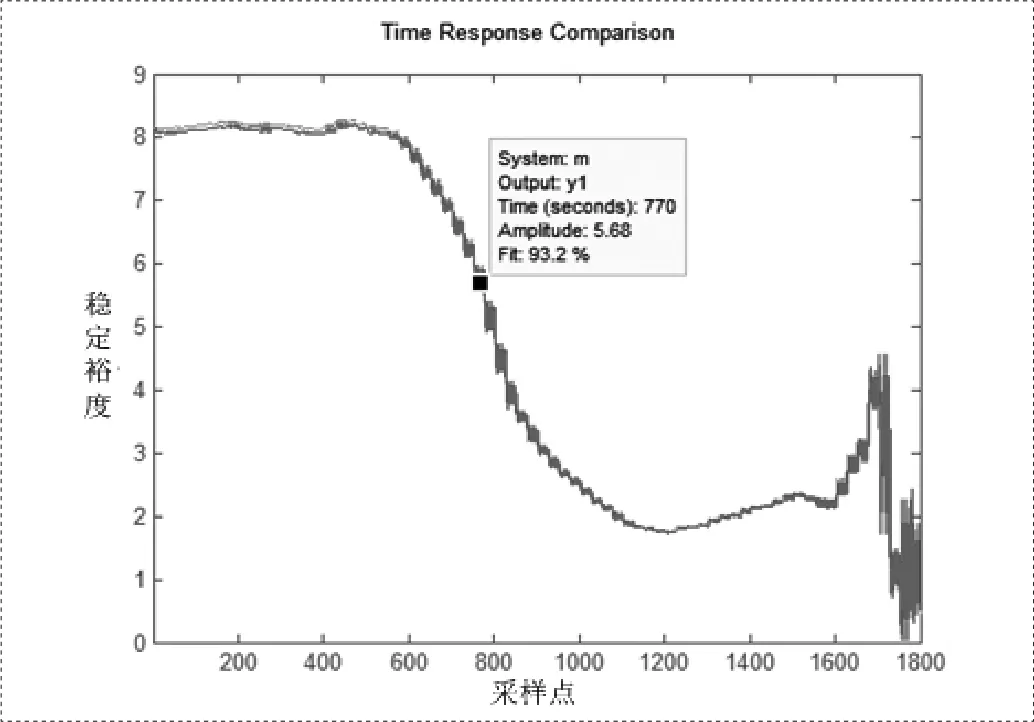
圖8 穩定裕度預測結果

穩定裕度的預測曲線和原始曲線如圖8中所示，紅色表示穩定裕度的預測值，灰色表示真實值，從圖中可以看出預測曲線的擬合度可以達到93.2%。

4 結論

1) 分析摔倒過程中的運動學特征，采用足底壓力中心點代替ZMP的方法確定人體穩定性的量化判別方法。

2) 通過摔倒過程中穩定裕度的自相關、偏相關系數，以及AIC判別準則，確定時間序列模型的類型和階數；采用最小二乘法對AR模型進行參數辨識，獲得最優的AR預測模型。

3) 采用AR時間序列模型對摔倒過程進行預測，獲得了比較好的預測曲線，為摔倒過程的穩定恢復控制策略研究提供了依據和基礎。

[1]伊蕾．助行康復機器人控制策略研究[D]．哈爾濱：哈爾濱工程大學,2012．

[2]Nishiwaki,K．and Kagami,S． Strategies for Adjusting the ZMP Reference Trajectory for Maintaining Balance in Humanoid Walking [C]．Proceedings of IEEE International Conference on Robotics and Automation,2010：4230-4236．

[3]Li．Q,Stankovic,J．A,Hanson,M．A, Barth．A．T,etc．Accurate．fast fall detection using gyroscopes and accelerometer-derived posture information[C]．In Proceedings of Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Charlottesville,2009：138-143．

[4]佟麗娜,宋全軍,葛云建．基于時序分析的人體摔倒預測方法[J]．模式識別與人工智能,2012,25/2：273-279．

[5]Q．Huang, K．Yokoi,S．Kajita,etc． Planning Walking Patterns for a Biped Robot [J]．IEEE Transaction on Robotics and Automation．2001：280-289．

[6]Peng Zhaoqin,Cao Chun,Huang Jiaoying．Human Moving Pattern Recognition toward Channel Number Reduction Based on Multipressure Sensor Network[J]．International Journal of Distributed Sensor Networks,2013．

[7]徐慧娟．自回歸AR模型的整體最小二乘分析研究[D]．南昌：東華理工大學,2012．

[8]Peter J．Brockwell,Richard A．Davis． Time Series：Theory and Methods[M]．Second Edition．Beijing：China Higher Education Press,2007：130-151．