零級超越亞純函數的q-差分多項式的值分布

金 瑾

(貴州工程應用技術學院 數學系循環經濟研究院, 貴州 畢節 551700)

零級超越亞純函數的q-差分多項式的值分布

金 瑾

(貴州工程應用技術學院 數學系循環經濟研究院, 貴州 畢節 551700)

利用Nevanlinna的亞純函數的值分布理論,研究零級超越亞純函數的q-微分多項式的值分布理論,討論差分多項式的特征函數和零點,取得一些結果,并且對差分多項式零點的一些經典結果建立差分模擬.

超越亞純函數; 差分多項式; 值分布; Nevanlinna理論

1 主要結果

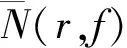
W. K. Hayman[1]證明了下面的著名定理.

定理1.1[1]設f(z)為超越亞純函數,n為正整數,如果n≥3,則fn(z)f′(z)取每一個非零有窮復數無窮多次.

L. R. Sons[2]證明了以下定理.

定理1.2[2](a) 若f(z)超越亞純函數,并且N1(r,1/f)=S(r,f),令

ψ=fn0(f′)n1…(f(k))nk,

其中n0、n1、n2、…、nk是非負整數,并且k≥1,n0≥1,如果

那么δ(a,ψ)<1,其中a≠0,∞.

(b)f(z)是超越亞純函數,

ψ=fn0(f′)n1…(f(k))nk,

若nk≥1,n0≥2,且

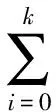
那么δ(a,ψ)<1,其中a≠0,∞.N. Steinmetz[3]進一步減弱了定理1.2的(b)條件,證明了以下定理.

定理1.3[3]若f(z)超越亞純函數,ψ=fn0(f′)n1…(f(k))nk,如果nk≥1,n0≥2,則

其中，c≠0,∞為一常數.

Jiang X. H.等[4]得到如下結論.

定理1.4[4]設f(z)為平面內的超越亞純函數,a為任意非零復數,對任意的正整數m,i0,i1,…,in,λ=i0+i1+…+in,Δ=i0+2i1+…+nin，則當m≥λ+Δ+2時,

wm+awi0(w′)i1(w(2))i1…(w(n))in

可取無窮多個零點.Fang M. L.[5]又研究了f(z)+a(f′(z))n的值分布,得到下面結論.

定理1.5[5]設f(z)為平面內的超越亞純函數,a為非零復數,對任意的正整數n≥2,函數f(z)+a(f′(z))n取每一個有窮復數無窮多次.

張然然等[6]研究了亞純函數的差分多項式

(1)

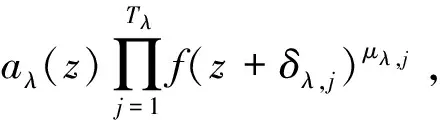
定理1.6設f(z)是有限級亞純函數,滿足N(r,f)=S(r,f),設H(z,f)形若(1)的差分多項式,其中系數是為f(z)的小函數,且H(z,f)中僅有一個單項式具有最高次數degfH,則

H(z,f)=(degfH)T(z,f)+S(z,f).

在本文中,令

F(z)=f(q0z)i0f(q1z)i1f(q2z)i2…f(qkz)ik,

(2)

其中，k≥1為整數,q1,q2,…,qk為相互不同的非零復常數,i1,i2,…,ik為非負整數,ai(z)為f(z)的小函數.

記i0+i1+…+ik=n=degfH,則有以下定理.

定理1.7設f(z)是零級超越亞純函數,滿足N(r,f)=S(r,f),設F(z)、k、n為(2)式所定義,又設H(z,f)為形如(1)式……