基于混合擴展卡爾曼濾波的超空泡航行體變深運動控制研究

白濤， 蔣運華， 韓云濤

(1.哈爾濱工程大學 自動化學院, 黑龍江 哈爾濱 150001; 2.哈爾濱工程大學 航天與建筑工程學院, 黑龍江 哈爾濱 150001)

基于混合擴展卡爾曼濾波的超空泡航行體變深運動控制研究

白濤1， 蔣運華2， 韓云濤1

(1.哈爾濱工程大學 自動化學院, 黑龍江 哈爾濱 150001; 2.哈爾濱工程大學 航天與建筑工程學院, 黑龍江 哈爾濱 150001)

為解決測量和環境噪聲導致的超空泡航行體在變深運動中的失穩問題，提出一種基于混合擴展卡爾曼濾波算法的控制方法。進行水洞實驗獲取超空泡航行體模型在控制過程中的測量和環境噪聲，采用這些數據改進了超空泡航行體的縱向運動數學模型；基于混合擴展卡爾曼濾波算法改進了超空泡航行體變深運動控制器。仿真結果表明，混合擴展卡爾曼濾波算法能夠有效地提高超空泡航行體變深運動的穩定性。

流體力學； 超空泡航行體； 變深運動控制； 水洞實驗； 混合擴展卡爾曼濾波

0 引言

超空泡水下航行體是一種利用超空泡技術來實現減阻、提速目的的水下航行體。超空泡技術是一種將水下航行體全部或大部分包裹在氣泡中，以減小航行體受到的流體阻力、提高航行體水下航行速度的技術[1]。由于超空泡航行體在水下完全或大部分包裹在氣體空泡中，其流體和控制特性都與傳統水下航行體有巨大的區別。

超空泡航行體在水下的巡航速度快(一般超過60 m/s)且其表面絕大部分被氣泡覆蓋，在航行過程中，超空泡航行體的運動穩定性受環境噪聲和測量噪聲的影響比傳統水下航行體受到的更劇烈，這種影響在超空泡航行體進行改變航行深度的運動時表現得最為明顯，給超空泡航行體變深運動的控制造成了極大的不確定性。

在超空泡航行體運動控制問題的研究方面，許多學者在理論和實驗研究方面發表了大量研究成果，代表性的有：Dzielski等[2]提出了一個縱向平面內的4狀態2自由度模型，該模型在保留超空泡航行體幾乎全部狀態信息情況下，具有結構簡單、易于分析的特點，被眾多研究超空泡航行體控制問題的文獻所引用[3-4]，已成為研究超空泡航行體控制問題的一個基準模型。Semennenko等[5]和Savchenko[6-7]對超空泡及超空泡航行體進行了大量有關流體力學的研究，包括數學建模、空泡形態計算及相關的流體力學水洞實驗等，特別是超空泡航行體穩定運動的4種受力平衡模式為超空泡航行體的控制提供了理論前提。Kim等[8]在初始條件確定的情況下采用充氣和空化器配合控制策略，對充氣空泡的超空泡航行體的深度控制進行了研究，并通過仿真進行了驗證。Sanabria等[9]在水洞中對超空泡航行體的縮比模型進行了一系列研究，得到了空化器在運動時的受力系數，在此基礎上重建了超空泡航行體的數學模型，并給出了測試數學模型和控制算法的測試平臺和方案。王京華等[10]和鄒望[11]使用精確線性化法對航行體的數學模型進行了簡化，并使用魯棒算法在內的控制算法設計了深度跟蹤控制器。李代金等[12]和范輝等[4]對超空泡航行體的數學建模、運動穩定性分析和彈道仿真等問題進行了研究。Wang 等[13]和Yuan等[14]在水洞中對不同固定空化器角度的超空泡航行體模型進行了水洞力學研究。Zhao等[15]使用μ分析等魯棒方法對超空泡航行體的運動控制進行了研究。

由以上研究成果可知，目前對超空泡航行體運動控制的研究多集中在使用仿真手段、在理論上對理想流體中超空泡航行體的控制進行研究，只有很少的研究者采用實驗測試手段進行研究。

由于在實際運動中，輸入超空泡航行體控制器的狀態信息均來源于傳感器，特別是空泡形態和航行體的深度目前還沒有直接、準確的測量手段，只能通過間接手段計算得到，而周圍環境的波動、傳感器自身的測量誤差和控制機構的執行誤差都影響著航行體的運動穩定性。可見，理論研究對應實際應用有著非常明顯的缺點，如：使用的噪聲數據不是實際測出的、使用的流體力學參數是在固定空化器轉角時測試得到的，等等。而控制研究關心的重點是控制器在控制過程中航行體狀態參數和相關噪聲的信息，需要以控制實驗為基礎才能夠得到。然而目前的實驗研究多集中在力學研究領域，很少涉及控制方面，目前已知的只有美國明尼蘇達大學建立了可以進行控制測試的測試平臺，但由于控制機構的松弛性[9]，很難進行精確的控制律測試。

因此，本文采用實驗研究和理論研究結合的方法，以超空泡航行體的變深運動為例，通過空化器可轉動的超空泡航行體模型的水洞實驗來測試噪聲對控制過程中航行體的各個參數的影響，然后對環境噪聲和測量噪聲對超空泡航行體運動穩定性的影響加以分析，并使用基于混合擴展卡爾曼濾波算法的控制器對超空泡航行體的變深運動進行控制。

1 超空泡航行體的數學模型

本文以超空泡航行體的變深運動為研究對象，建立超空泡航行體縱向運動的數學模型。參考文獻[2]中的模型，在縱向平面內選用航行體的體坐標系Oxbzb進行建模分析，航行體受力如圖1所示。

圖1 超空泡航行體示意圖Fig.1 Configuration of supercavitating vehicle

圖1中，航行體總長度為L，重心到空化器的中心的距離為Lc；航行體主要受到垂直于空化器平面的空化器力Fc、沿zg軸方向垂直向下的重力G、沿xb軸指向重心O的推力FT和尾部受到的滑行力FP，其方向為垂直于航行體尾部露出空泡的彈體平面。為分析方便，約定v為航行體重心的前進速度，其方向與xg軸方向相同，并假設v的數值和方向在整個運動過程中是恒定的；攻角α為xb軸與速度v的夾角；俯仰角θ為xb軸和xg軸的夾角，且α=θ，要求俯仰角為小角度(小于5°)，則有sinθ≈θ，cosθ≈1；δc和δf為空化器和尾翼的偏轉角，是超空泡航行體的主要控制參數，以逆時針旋轉為正。

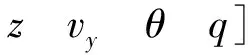
(1)

(2)

(3)

(4)

(5)

具體參數見文獻[3]。

超空泡航行體在實際航行和控制過程中，不可能存在理論計算中的理想環境，主要狀態參數如縱向速度、俯仰角、俯仰角速度、泡內壓力等都來自于航行體內部的測量設備，一些關鍵參數如航行體的深度則來自這些參量的計算，考慮設備自身的精度和航行過程中的干擾，這些包含干擾的測量參量必然會對航行體的運動穩定性產生影響。根據對數學模型的分析，航行體尾部的滑行力兼具了非線性和突變性的特點，對航行體運動穩定性影響最大，因此本文只對產生滑行力的航行體尾部探出空泡的距離h在環境和測量噪聲影響下的變化進行研究，進而研究航行體在變深運動中的穩定控制問題。

2 噪聲對超空泡航行體運動穩定性的影響

由于超空泡航行體在實際運動過程中的環境條件千變萬化，很難判斷環境和測量噪聲的形式和量級，本文以超空泡航行體模型在一次水洞實驗中的實驗數據作為判定環境和測量噪聲的形式和量級的依據。為更真實地反映超空泡航行體在實際運動過程中的狀態，本次實驗采用空化器可開環控制的模型，測試空化器轉動時(模擬航行體的控制過程)的測量參數和實際空泡形態數據，從而根據(4)式判斷噪聲對h的影響。

本次實驗在重力水洞中進行，對具有圓盤形空化器的超空泡航行體進行空化器開環運動的測試實驗，實驗布置如圖2所示。

圖2 實驗環境示意圖Fig.2 Experimental environment

模型的圓盤空化器直徑0.02 m，模型長度0.22 m，模型直徑0.02 m； 水洞內流速9.69 m/s，預期充氣空化數為0.1. 實驗中，測量兩個壓力數值，一個由固定在水洞蓋板上的壓力傳感器采集泡外壓力；一個由連接在模型表面的軟管引出到模型尾部，由模型尾部的小型壓力傳感器采集模型表面(泡內)的壓力。

實驗中空化器的運動由外部電機帶動，空化器的運動幅度為±30°，考慮到控制機構的限制，采用0.5 Hz的轉動頻率，(實際運動中，空化器的偏角達到峰值時由于鋼絲的彈性原因會產生一定的延時)定義空化器順時針轉動為正，逆時針轉動為負。

整個實驗首先在水流靜止時開始充氣，同時啟動壓力測試系統和錄像系統，當氣量穩定時啟動水流；水流速度穩定后，開始啟動電機驅動空化器轉動并同時開始計算實驗時間，實驗持續時間一般為30 s，之后水流速度減緩直至停止，所有設備停止并提取實驗數據。

空泡形態隨空化器的轉動變化如圖3所示。

圖3 水洞實驗過程圖Fig.3 Experimental process of water tunnel

圖4 空化數Fig.4 Cavitation number

根據得到的空泡內外壓力求取空化數[2]，得到空化數如圖4所示，可見所求空化數在航行體穩定時在0.1附近振蕩，符合實驗預期。

通過對視頻圖片的測量，取得模型尾部(距離空化器中心0.2 m處)下半部分的空泡半徑數據，將其與對應的空化器轉角在圖5中畫出，并同時給出通過固定空化數為0.1時，在相同位置處的空泡半徑[5]。由于實驗數據量較大，因此將同一空化器偏轉角對應的空泡半徑實驗數值去掉明顯不合理的數值，其余取平均值，從而得到圖5中的實驗數據值。

圖5 空泡半徑的理論計算與實驗數據Fig.5 Comparison of theoretical and experimental data of radius of supercavity

根據圖5可知，空泡半徑的實驗數值與理論計算值一系列差值ΔRc的最大值不超過Rc理論值的10%，可見航行體尾部空泡半徑Rc的實際值是其理論計算值與一個以其10%幅值為最大值的白噪聲信號的差值。本文只針對某一個點進行空泡半徑的分析和測量，由空泡形態的理論計算公式可知，其整體空泡形態的計算具有連續性，空泡其他位置的半徑也應符合以上結論。因此本文以此計算超空泡航行體在控制過程中的空泡形態真實值。

由文獻[3-5]可知，超空泡航行體控制過程中的最大問題是滑行力的計算，其關鍵是超空泡航行體尾部探出空泡的長度h，而空泡形態計算的主要目的之一就是計算h. 以上文分析為基礎，可知超空泡航行體尾部探出空泡長度h的誤差范圍是航行體尾部探出空泡處的空泡半徑計算值的10%.

本文研究的重點是將實驗中的實際環境誤差代入理論模型，實現對超空泡航行體在該種實際干擾環境下的控制仿真研究。為在等價條件下簡化研究過程，將實驗中由充氣、水流、機械傳動、測量等因素綜合造成的空化數誤差導致的空泡半徑誤差以及進一步導致的h誤差，統一認為是由vy的測量誤差造成的，也就是將產生誤差的環境和測量噪聲都歸結于vy的測量噪聲。因此，在固定空化數為0.1的條件下，將產生滑行力處的ΔRc的最大值0.01 m代入(3)式，則求得Δvy的最大振蕩幅度為0.021 16 m/s，此值為代入最大值計算得到，故將vy的測量噪聲以最大幅值為0.02 m/s的白噪聲形式表示。

為研究此種環境下噪聲對航行體變深控制的影響，使用參考文獻[4-5]中的控制律形式，對有、無噪聲時的控制運動曲線進行對比，使用的控制器均如(6)式所示：

(6)

令初始狀態為(0 m,0 m/s,0°,0°/s)，在無噪聲情況下，其運動仿真曲線如圖6所示。假設航行深度為相對深度，在初始時刻之前，航行體保持在穩定直航狀態，在0 s時刻接到變深命令，開始進行變深運動。

圖6 超空泡航行體變深運動過程(無噪聲干擾)Fig.6 Variable-depth motion process of supercaviting vehicle (without noise)

可見超空泡航行體在控制律((6)式)下，能夠穩定在相對初始深度為0.7 m的位置穩定航行，但是若加入擾動且縱向速度vy為以0.1 s為周期離散采集后，其運動過程如圖7所示。

圖7 超空泡航行體運動過程(有噪聲干擾)Fig.7 Variable-depth motion process of supercaviting vehicle (with noise)

由此可見，原控制律在有噪聲擾動時已經不能達到穩定運動的控制要求，若想實現穩定的控制，則需要對出現的噪聲擾動進行處理。

3 混合擴展卡爾曼濾波算法

針對以上分析結果，本文提出使用混合擴展卡爾曼濾波技術，處理系統噪聲和量測噪聲對超空泡航行體變深運動控制的干擾問題。擴展卡爾曼濾波是一種使用線性化方法對非線性系統的狀態進行估計的算法，而混合擴展卡爾曼濾波算法尤其適用于描述系統是連續時間系統而量測的狀態量是離散的情況，而這種特性正是超空泡航行體在實際運動時所對應的情況[16]，因此本文使用混合卡爾曼濾波算法對第2節提出的問題進行處理。

混合擴展卡爾曼濾波算法假設一個帶有離散的量測狀態量的連續時間系統如下：

(7)

式中：過程噪聲ω(t)為協方差為Q的連續時間白噪聲；信號的測量噪聲vk為協方差為Rk的離散時間的白噪聲。

通用卡爾曼濾波方程如(8)式所示：

(8)

在每一個測量點，按照離散卡爾曼濾波方程更新狀態估計和協方差如下：

(9)

若系統給出的量測方程如(7)式所示，則具體運算過程如下：

1)初始化濾波器如(10)式所示：

(10)

2) 將(10)式的初始值代入(11)式，

(11)

4) 在k時刻將量測值yk代入狀態估計和協方差表達式(12)式中：

(12)

5) 由(12)式的解返回(11)式，轉到步驟3，實現下一步的運算。

運算過程具體介紹詳見文獻[17]。

4 仿真驗證

令x=(0 m,0 m/s,0°,0°/s)為初始狀態，將模型(1)式代入(7)式和(8)式中進行計算，得

(13)

環境噪聲ω=0由假設得到，則Q=0；測量噪聲v0是最大幅值為0.02 m/s的白噪聲，取測量樣本為2 000，按圖5的數值計算，則其協方差Rk約為10-4，Ak如(14)式所示：

(14)

將第3節中的濾波算法結合控制器((6)式)代入仿真模型，得到如圖8所示的仿真圖，仿真采樣頻率為10 Hz.

圖8 超空泡航行體變深運動比較圖Fig.8 Comparison of variable-depth motions of supercaviting vehicle

經比較可見，加入干擾噪聲后航行體深度的理論值和加入干擾后實際值之間的均方差為0.15 m，無大的跳變，運動軌跡基本保持穩定。由此可知，混合擴展卡爾曼濾波算法有效地輔助了控制器，使超空泡航行體在變深運動中保持了穩定。

5 結論

本文以一種水洞環境中空化器動態時的超空泡形態測試實驗數據為基礎，通過等價代換原則，將實際干擾噪聲代入理論模型，在有、無噪聲干擾情況下分別對同一數學模型、同一控制器超空泡航行體的變深控制問題進行了仿真研究，提出了混合擴展卡爾曼濾波方案。研究結果表明，使用混合擴展卡爾曼濾波方法能夠有效地保證超空泡航行體在變深運動時的穩定，若希望實現更理想的效果，需要對濾波算法進行進一步的研究，并輔以更加合適的控制器。該結論來自針對本文實驗環境數據進行的仿真分析，如果要得到能夠應用于實際環境的控制方法，還需要大量的實驗數據和真實湖試數據作為基礎。

References)

[1] Logyingvich G V. Hydrodynamics of flows with free boundaries [M].Kiev, Russian: Naukova Dumka Publishing House, 1980.

[2] Dzielski J, Kurdila A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions [J]. Journal of Vibration and Control, 2003, 9(7): 791-804.

[3] 范輝, 張宇文. 超空泡航行器穩定性分析及其非線性切換控制[J].控制理論與應用, 2009, 26 (11):1211-1217.

FAN Hui, ZHANG Yu-wen. Stability analysis and nonlinear switching controller design for supercavitating vehicles [J]. Control Theory & Applications， 2009，26 (11):1211-1217.(in Chinese)

[4] Lin G J, Balachandran B, Abed E H. Nonlinear dynamics and bifurcations of a supercavitating vehicle[J]. IEEE Journal of Oceanic Engineering, 2007, 32(4): 753-761.

[5] Semennenko V N. Physics and calculation [C]∥RTO AVT Lecture Series on Supercavitating Flows. Brussels, Belgium: Von Karman Institute, 2001: EN-010-11.

[6] Savchenko Y N. Control of supercavitation flow and stability of supercavitating motion of bodies [R]. Ukrainian: National Academy of Sciences-Institute of Hydro-mechanics, 2001.

[7] Savchenko Y N. Experimental investigation of supercavitating motion of bodies [C]∥RTO AVT Lecture Series on Supercavitating Flows. Brussels, Belgium: Von Karman Institute, 2001: EN-010-04.

[8] Kim S,Kim N. Control strategy for a ventilated supercavitating vehicle in initial phase [J] International Journal of Offshore and Polar Engineering, 2016, 26(2): 132-138.

[9] Sanabria D E, Balas G, Arndt R. Modeling, control, and experimental validation of a high-speed supercavitating vehicle [J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 362-373.

[10] 王京華，魏英杰，曹偉，等.水下超空泡航行體非線性動力學建模與仿真[J].工程力學， 2011, 28(12): 183-189.

WANG Jing-hua, WEI Ying-jie, CAO Wei, et al. Nonlinear dynamic modeling and simulation of an underwater supercavitating vehicle [J]. Engineering Mechanics, 2011, 28(12): 183-189.(in Chinese)

[11] 鄒望.基于Logvinovich 原理的通氣超空泡理論及其數值研究[D].哈爾濱： 哈爾濱工業大學，2013.

ZOU Wang. Theoretical and numerical research [D]. Harbin： Harbin Institute of Technology，2013.(in Chinese)

[12] 李代金，羅凱，黨建軍,等 .超空泡水下航行器空間運動建模與彈道仿真[J].兵工學報,2012, 33(8): 956-961.

LI Dai-jin, LUO Kai, DANG Jian-jun, et al. Kinematic modeling and trajectory simulation for underwater supercavitating vehicles [J]. Acta Armamentarii, 2012, 33(8): 956-961 .(in Chinese)

[13] Wang Y D, Yuan X L, Zhang Y W. On the reentrant jet of a supercavitating body [C] ∥Proceedings of the 8th International Symposium on Cavitation. Singapore:Research Publishing Services,2012：916-921.

[14] Yuan X L, Wang Y D. Experimental studies on hydrodynamic characterstic of supercavitating vehicles [C] ∥Proceedings of the 8th International Symposium on Cavitation. Singapore:Research Publishing Services,2012：879-884.

[15] Zhao X H, Sun Y, Zhao G L, et al.μ-synthesis robust controller design for the supercavitating vehicle based on the BTT strategy[J]. Ocean Engineering, 2014,88(11):280-288.

[16] Simon D. 最優狀態估計:卡爾曼,H∞及非線性濾波[M].張勇剛, 李寧, 奔粵陽,譯.北京:國防工業出版社,2013:300-303.

Simon D. Optimal state estimation: Kalman,H∞, and nonlinear approaches[M].ZHANG Yong-gang, LI Ning, BEN Yue-yang, translated. Beijing: National Defense Industry Press, 2013:300-303. (in Chinese)

ResearchonVariable-depthMotionControlofSupercavitingVehicleBasedonHybridExtendedKalmanFilter

BAI Tao1， JIANG Yun-hua2， HAN Yun-tao1
(1.College of Automation, Harbin Engineering University, Harbin 150001, Heilongjiang, China; 2.College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

A control method based on hybrid extended Kalman filter is proposed to solve the lose control during variable-depth motion of supercavitating vehicle caused by measured and environmental noises. The math model of supercavitating vehicle is improved based on the measured and environmental noises obtained by experiment in water tunnel. The control law is improved by using hybrid extended Kalman filter for variable-depth motion of supercavitating vehicle. Simulated result shows that the the hybrid extended Kalman filter can be used to improve the motion stability of supercavitating vehicle during variable-depth motion.

fluid mechanics； supercavitating vehicle; variable-depth motion control; experiment in water tunnel; hybrid extended Kalman filter

2017-02-10

國家自然科學基金項目(51309058、51209049)

白濤(1978—)，男，講師，博士。E-mail:baitao1@hrbeu.edu.cn

TJ630.1

A

1000-1093(2017)10-1980-08

10.3969/j.issn.1000-1093.2017.10.014