平衡超立方體的故障容錯性

張欣欣，許力，林麗美,3

?

平衡超立方體的故障容錯性

張欣欣1,2，許力1,2，林麗美1,2,3

（1. 福建師范大學數學與計算機科學學院，福建福州 350007；2. 福建省網絡安全與密碼技術重點實驗室，福建福州 350007；3. 福建農林大學計算機信息學院，福建福州 350002）

故障容錯是衡量多處理器互連網絡可靠性的重要方式之一。其中-限制邊連通度和-限制連通度保證了剩下每個分支之間不連通且每個分支中節點的鄰居數目不少于，能夠更加精準地測量多處理器和多信道系統的容錯性和可靠性。平衡超立方體是超立方體的一個變形，它特有的良好拓撲性質能夠更好地滿足多處理器系統和多種新型網絡的需要。提出了維平衡超立方體的{1,2}-限制邊連通度和{1,2}-限制連通度，能夠豐富以平衡超立方體為拓撲結構的網絡容錯性和可靠性的評價體系，并為平衡超立方體的故障診斷算法打下良好基礎。

故障容錯性；限制連通度；限制邊連通度；平衡超立方體

1 引言

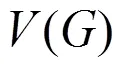
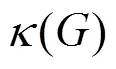
連通度（邊連通度）測量容錯性有3個明顯的缺陷：① 2個網絡的連通度（或邊連通度）即使相同，它們的可靠性也不一定一樣，因為它們的最小點割（或最小邊割）故障概率可能不同；②連通度（邊連通度）不能準確地反映由于處理機（或通信信道）損壞造成的系統損壞程度；③在分析和應用這2個參數時，本文不言而喻地假定了系統的任何部件都可能同時失靈[4]。為了彌補以上缺陷，人們對傳統的連通度（邊連通度）概念加以推廣，以適應網絡容錯性分析的需要。本文研究的限制邊連通度和限制連通度就是連通度和邊連通度的推廣。

超立方體被稱為并行計算系統中最流行的互連網絡拓撲結構之一,Bhuyan[18]提出了各種性能優良的超立方體網絡的變形，經過多年的發展，新型互連網絡已經提出一系列的拓撲結構，包括折疊立方網絡、交叉立方網絡、交換立方網絡、分層立方網絡和平衡超立方網絡等。由Wu和Huang[19]提出的平衡超立方體增強了超立方體的一些性質。平衡超立方體中每個點都有一個與自己鄰點相同的匹配節點，故在平衡超立方網絡中一個故障節點的運行任務可以轉化給它的匹配節點完成[20]。迄今為止，平衡超立方體的容錯性與可靠性研究尚未求出。

2 平衡超立方體的定義與性質

平衡超立方體的定義由Wu和Huang[19]用2種方式提出。

圖1是一維平衡超立方體和二維平衡超立方體的結構圖。

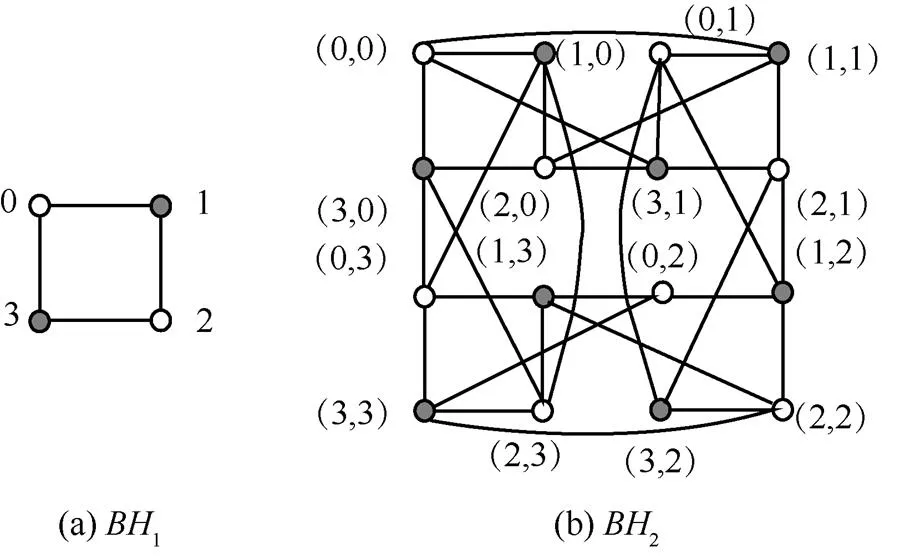
圖1 一維和二維平衡超立方體結構

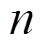
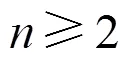
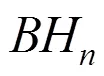
3 平衡超立方體的限制邊連通度

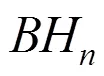
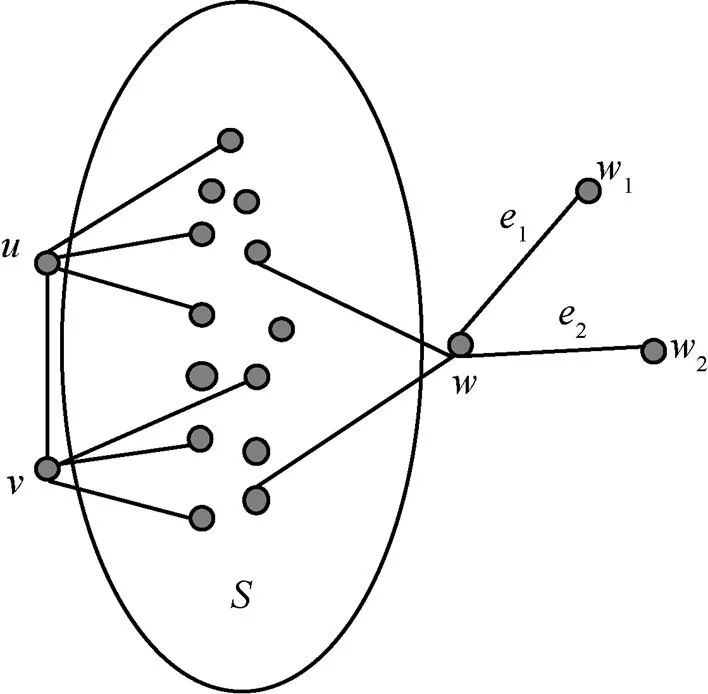
圖2 ，都不在S中

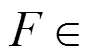
4 平衡超立方體的限制連通度

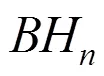
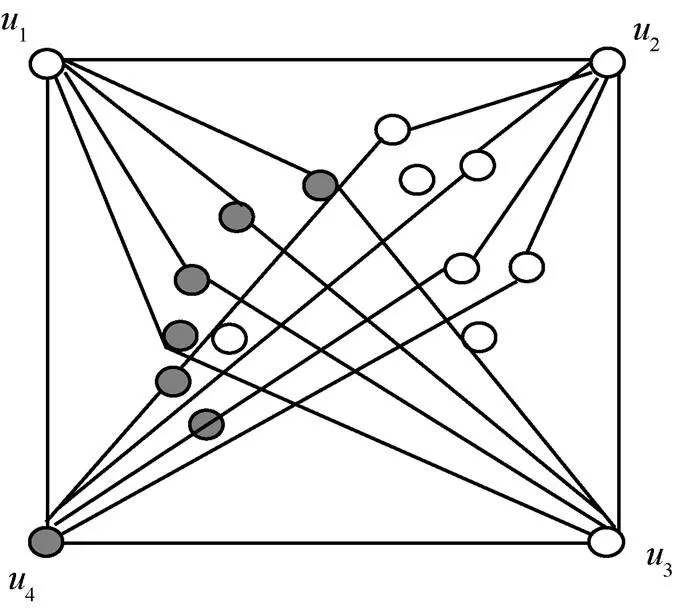
圖3 圈C的鄰邊集

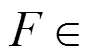
圖4 圈C的鄰點集

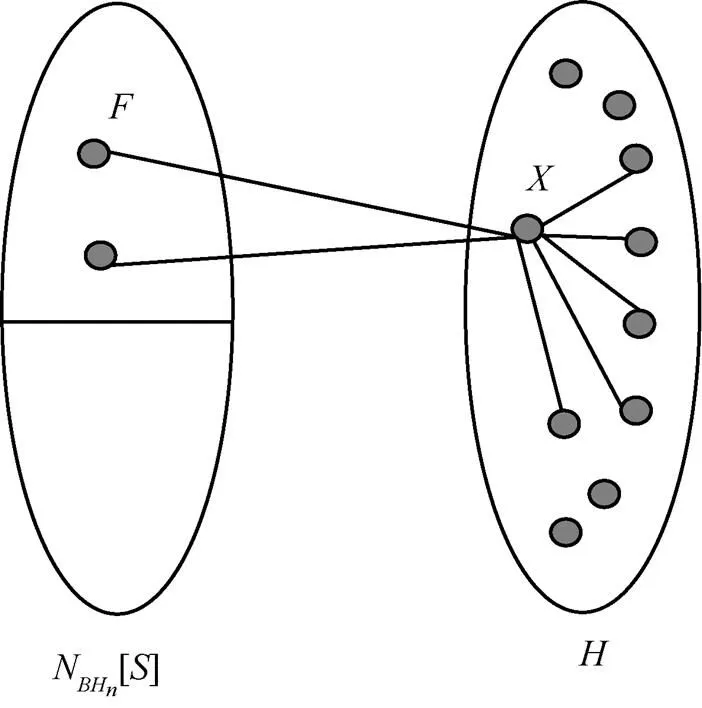
圖5 F是的2-限制點割

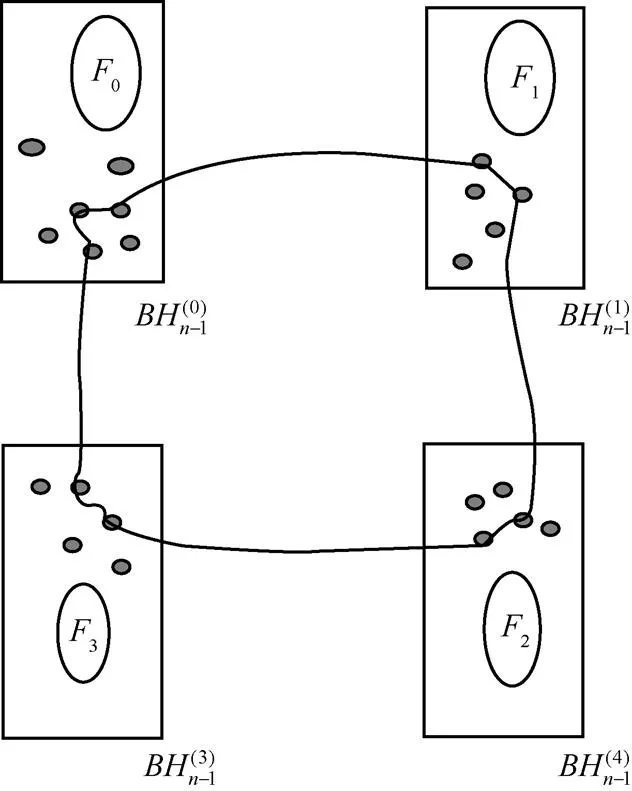
圖6 是連通的

圖7 是連通的

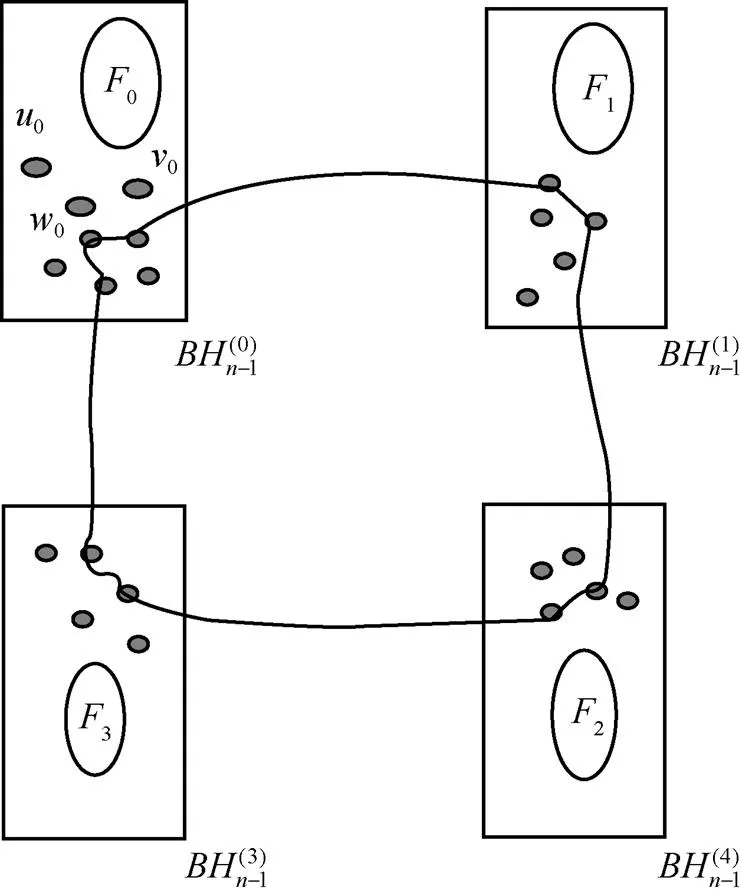
圖8 是連通的

圖9 是連通的

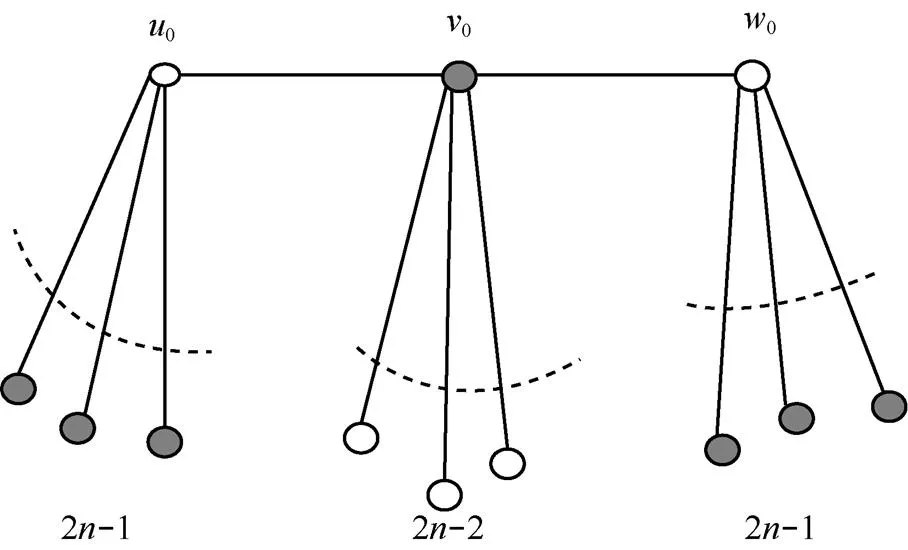
圖10

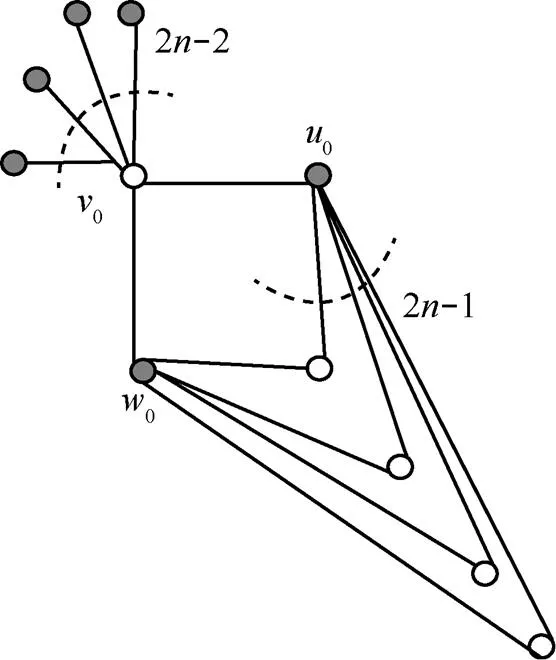
圖11

5 結束語

[1] 包國華, 王生玉, 李運發. 云計算中基于隱私感知的數據安全保護方法研究[J]. 信息網絡安全, 2017(1):84-89. BAO G H,WANG S Y, LI Y F. Research on privacy aware data security protecting method in cloud computing[J]. Netinfo Security, 2017(1):84-89.

[2] 周濤, 柏文潔, 汪秉宏, 等. 復雜網絡研究概述[J]. 物理, 2005, 34(1): 31-36. ZHOU T, BAI W J,WANG B H, et al. Overview of complex network Research[J]. PHYSICS, 2005, 34(1): 31-36.

[3] 滑楠, 曹志剛. 無線認知網絡概念與實例研究[J]. 計算機工程與應用, 2009, 45(2): 1-6. HUA N, CAO Z G. The concept and examples of wireless cognitive Network[J]. Computer Engineering and Applications, 2009, 45(2): 1-6.

[4] 徐俊明. 組合網絡理論[M]. 北京: 科學出版社, 2007.

XU J M, Combinatorial theory in networks[M]. Beijing: Science Press,2007.

[5] 徐俊明. 圖論及其應用[M]. 合肥: 中國科學技術出版社, 2010.

XU J M, Graph Theory with Applications[M]. Hefei: Science and Technology of China Press,2010.

[6] XU J M, ZHU Q, XOU X M, et al. On restricted connecti-vity and extra connectivity of hypercubes and folded hypercubes[J]. Journal of Shanghai Jiaotong University (Science), 2005, 10(2): 203-207.

[7] LIN L M, XU L, ZHOU S M, et al. The extra, restricted connectivity and conditional diagnosability of split-star networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(2): 533-545.

[8] LIN L M, ZHOU S M. Conditional connectivity for (n, k)- arrangement graphs[J]. Journal of Mathematical Study, 2012, 45(4): 350-364.

[9] 林麗美, 周書明, 許力. 分層立方網絡的/-診斷度和診斷算法[J]. 山東大學學報(理學版). 2013, 48(7):85-92. LIN L M, ZHOU S M, XU L./- diagnosability and diagnosis algorithm for hierarchical cube networks[J]. Journal of Shandong University(Natural Science), 2013,48(7):85-92.

[10] ZHOU S, CHEN L, XU J M. Conditional fault diagnosability of dual-cubes[J]. International Journal of Foundations of Computer Science, 2012, 23(8): 1729-1748.

[11] ZHOU S, XU J M. Conditional fault tolerance of arrangement graphs[J]. Inform Process. 2011, 111(21): 1037-1043.

[12] ZHU Q, XU J M. On restricted edge connectivity and extra edge connectivity of hypercubes and folded hyper cubes[J]. Journal of University of Science and Technology of China, 2006, 36(3): 249-251.

[13] PAN X F, XU J M, LV M. On restricted connectivity of some cartesian product graphs[J]. Journal of University of Science and Technology of China, 2006, 36(3):237-240.

[14] 王國亮, 師海忠. 完全對換網絡的限制連通度[J]. 運籌學報, 2013, 17(3): 57-64.

WANG G L, SHI H Z. The restricted connectivity of completely switched networks[J]. Operations Research Transactions, 2013, 17(3): 57-64.

[15] 馬強, 梁家榮, 熊茜, 等. 交換交叉網絡的可靠性研究[J]. 高技術通訊, 2015, 25(10):919-926.

MA Q, LIANG J R, XIONG Q, et al.Research on reliability of switched cross networks[J]. High Technology Letters,2015, 25(10): 919-926.

[16] XU J M, LV M, FAN Y M. The restricted edge-connectivity of de Bruijn undirected graphs[J]. Ars Combinatoria Waterloo then Winnipeg, 2008, 83(1):321-333.

[17] 徐俊明，點可遷圖的限制邊連通度[J]. 數學年刊A輯(中文版), 2000, 21(5):266-272.

XU J M. Restricted edge connectivity of vertex transitive graphs[J]. Chinese Annals of Mathematics,Series A.2000, 21(5):266-272.

[18] BHUYAN L N, AGRAWAL D P. Generalized hypercube and hypercube structures for a computer network[J]. IEEE Trans Computers, 1984,32(4):323-333.

[19] WU J, HUANG K. The balanced hypercube: a cube-based systemhemat for fault-tolerant applications[J]. IEEE Transactions Comput, 1997, 46(4): 484-490.

[20] ZHOU J X, WU Z L, YANG S C, et al. Symmetric proper and reliability of balanced hypercube[J]. IEEE Transactions Comput, 2015, 64(3): 876-881.

[21] LU H Z. On extra connectivity and extraedge-connectivity of balanced hyper cubes[J]. International Journal of Computer Mathematics, 2016, 94(4): 813-820.

[22] YANG M C. Super connectivity of balanced hyper cubes[J]. Applied Mathematics and Computation, 2012, 219(3): 970-975

Fault tolerance of balanced hypercubes

ZHANG Xin-xin1,2, XU Li1,2, LIN Li-mei1,2,3

(1. School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, China;2. Fujian Provincial Key Laboratory of Network Security and Cryptology, Fuzhou 350007, China;3. College of Computer and Information Science, Fujian Agriculture and Forestry University, Fuzhou 350002, China)

Fault tolerance is one of the important ways to measure the reliability of multiprocessor interconnection networks.-restricted edge connectivity and-restricted connectivity can ensure every remaining component is disconnected , the number of neighbors of vertex is no less than, which can measure the fault tolerance and reliability of multiprocessor and multichannel system more accurately. Balanced hypercubes is a variant of the hypercube, which has some specific topological properties, it can better meet the needs of the multiprocessor system and many new networks. The {1,2}-restricted edge connectivity and the {1,2}-restricted connectivity of balanced hypercubes were proposed, which could enrich the evaluation system of network fault tolerance and reliability in balanced hypercubes topology and it laid a good foundation for the fault diagnosis algorithm of balances hypercube.

fault tolerance, restricted connectivity, restricted edge-connectivity, balanced hypercubes

O157.5

A

10.11959/j.issn.2096-109x.2017.00193

2017-06-15；

2017-08-17。

許力，Xuli@fjnu.edu.cn

國家自然科學基金資助項目（No.61771140, No.U1405255, No.61702100）；福州市科技局基金資助項目（No.2015-G-59）；福建省高校產學合作科技重大基金資助項目（No.2017H6005）；福建省教育廳基金資助項目（No.JAT160123）；中國博士后面上基金資助項目（No.2017M612107）

The National Natural Science Foundation of China (No.61771140, No.U1405255, No.61702100), Fuzhou Science and Technology Bureau Project (No.2015-G-59), University Industry Cooperation of Major Science and Technology Project of Fujian Province (No.2017H6005), Fujian Provincial Education Department Project (No.JAT160123), Post-doctoral Science Foundation of China (No.2017M612107)

張欣欣（1993-），女，河南羅山人，福建師范大學碩士生，主要研究方向為網絡與信息安全。

許力（1970-），男，福建福州人，博士，福建師范大學教授、博士生導師，主要研究方向為網絡與信息安全。

林麗美（1988-），女，福建莆田人，博士，福建農林大學講師，主要研究方向為網絡與信息安全。