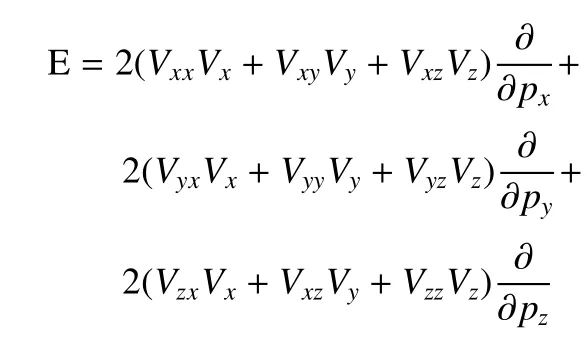基于混合Lie算子辛算法的不變流形計算1)

鄭丹丹 羅建軍 ,2) 張仁勇 劉 磊

?(西北工業大學航天學院，西安710072)

?(航天飛行動力學技術重點實驗室，西安710072)

??(中國科學院空間應用工程與技術中心，北京100094)

??(北京飛行控制中心，北京100094)

基于混合Lie算子辛算法的不變流形計算1)

鄭丹丹?,?羅建軍?,?,2)張仁勇??劉 磊?,??

?(西北工業大學航天學院，西安710072)

?(航天飛行動力學技術重點實驗室，西安710072)

??(中國科學院空間應用工程與技術中心，北京100094)

??(北京飛行控制中心，北京100094)

平動點附近周期軌道的不變流形因其在低能軌道轉移中起著重要作用而受到廣泛關注.在設計低能軌道過程中不變流形要實時進行能量匹配，但利用傳統數值積分方法進行積分時能量會耗散.顯式辛算法具有比隱式辛算法計算效率高的優勢，但其要求Hamilton系統必須分成兩個可積的部分，而旋轉坐標系下的圓型限制性三體問題是不可分的，因而顯式辛算法難以用于求解旋轉坐標系下的圓型限制性三體問題.本文通過引入混合Lie算子，成功實現了帶三階導數項的力梯度辛算法對圓型限制性三體問題的求解，并將基于混合Lie算子的帶三階導數項的辛算法與Runge-Kutta78算法和Runge-Kutta45算法進行仿真對比，仿真結果表明基于混合Lie算子的含有三階導數項的辛算法位置精度高、能量誤差小且計算效率高.利用基于混合Lie算子的帶三階導數項的辛算法計算不變流形，可以實現低能軌道轉移過程中軌道拼接點的能量精準匹配.

圓型限制性三體問題，不變流形，辛算法，混合Lie算子

引言

平動點[1]是限制性三體問題中的動平衡點，在隨兩個天體一起旋轉的參考系中處于靜止狀態.它們是幾何意義上的點，其本身的應用價值十分有限.真正引人關注的是其周圍大量存在的周期軌道[2]，以及與之相聯的管狀不變流形[3](包括穩定流形和不穩定流形).周期軌道是完成某些特殊任務的理想場所，而不變流形則提供了往返于主天體和周期軌道之間的低能耗轉移途徑[49].太陽系中不同三體系統平動點周期軌道的不變流形還存在相交的情形，從而拓展了系統間的深空轉移軌道設計范圍，因此尋找航天器從地球停泊軌道到平動點附近周期軌道的轉移軌道顯得尤為重要.

20世紀90年代，G′omez等[10]引入非線性動力系統理論，利用穩定流形將航天器送到了平動點附近，是轉移軌道設計[11]的重大突破.這一發現不但節省了能量也為星際超級公路理論的誕生奠定了基礎.但是不論是日--地系統還是地--月系統，不變流形距離地球都比較遠，需要在推力或引力輔助[12]作用下將航天器從地球停泊軌道轉移到穩定流形上.由于在優化拼接點時需要多次計算不變流形，如何選取不變流形的拼接點是進行低能軌道轉移設計的關鍵.已經有學者對不變流形的計算進行研究，Zhang等[13]利用三次回旋插值法計算圓型限制性三體問題不穩定平動點周期軌道的不變流形，Lei等[1417]利用Lindstedt-Poincar′e方法求解了限制性三體和四體平動點周期軌道不變流形的高階近似解析解，Dellnitz等[18]提出了方向集數值計算方法，Howell等[19]利用胞映射法[20]描述和存儲不變流形的數據.這些計算方法提高了不變流形的計算速度，但是卻沒有關注不變流形的能量變化.由于圓型限制性三體問題是一個非線性自治哈密頓系統，沒有嚴格的解析解，而且由于強非線性其對初值誤差十分敏感，較小的計算誤差將導致微分方程的解較大地偏離實際情況.因此需要尋找一種保能量的不變流形計算方法.

普通數值解法具有人為耗散性，長時間計算會導致系統總能量的耗散隨時間的平方增長.在研究三體問題的過程中，對辛結構的破壞無疑會對動力學特性造成很大影響，使得系統的長期演化不能真實反映客觀事實.辛積分方法[2122]由于具有保辛結構和能量守恒兩個重要特性，近年來得到了快速發展[2326].顯式辛算法具有比隱式辛算法計算效率高的優勢，但其要求Hamilton系統必須可以分成兩個可積的部分.旋轉坐標系下的圓型限制性三體問題由于受Coriolis力的影響，不能像慣性系下的系統一樣可分，因此，從形式上看顯式差分格式對其不適用.廖新浩等[27]將圓型限制性三體問題的Hamilton函數分成動能與勢能的和以及由坐標旋轉產生的非慣性力兩部分，然后利用算法合成構造差分結構，計算復雜.Sun等[28]分析了帶有三階導數項的力梯度辛算法在保能量上的優勢，但是沒有將該算法應用在旋轉坐標系下的圓型限制性三體問題中，也沒有將辛算法用在不變流形的求解上.

鑒于顯式辛算法不適合求解旋轉坐標系下圓型限制性三體問題，本文通過重新定義類動能的Lie算子，嚴格證明基于混合Lie算子的含有三階導數項的顯式辛算法可以求解旋轉坐標系下的圓型限制性三體問題.首先，給出文中所用的動力學模型和不變流形的計算方法；然后，建立混合Lie算子并研究顯式辛算法在求解Hamilton系統類動能不具有標準二次型的圓型限制性三體問題時的可行性；最后，將本文改進算法與 Runge-Kutta78(RK78)和 Runge-Kutta45(RK45)[29]算法進行仿真對比.

1 空間圓型限制性三體問題

1.1 動力學模型

圓型限制性三體問題描述的是質量為m3的航天器P3在兩個繞著共同質心做勻速圓周運動的主天體P1和P2的引力場下運動，其質量分別為m1和m2，且m3?m1?m2，以P1和P2的質心為原點，P1指向P2的方向為x軸，y軸在兩個主引力體旋轉平面上，z軸垂直于xy平面，滿足右手法則，如圖1所示.

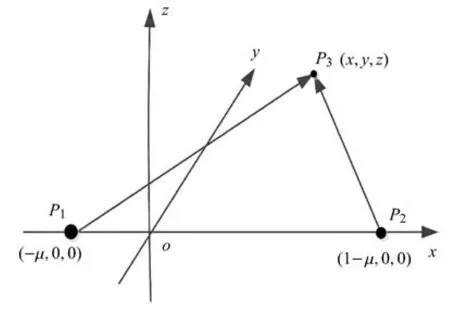
圖1 圓型限制性三體問題Fig.1 Circular restricted three-body problem

假設P3在oxy平面運動，為了簡化模型，對單位進行無量綱化處理.令引力常量G、主天體P1和P2之間的距離、旋轉角速度ω、質量和均為1，因此 P1的質量為1?μ=m1/(m1+m2)，位置坐標為(?μ,0,0)，P2的質量為 μ =m2/(m1+m2)，位置坐標為(1?μ,0,0).文中所有量如無特殊說明都是無量綱的.在此旋轉坐標系下航天器的運動方程和Largrange函數[30]分別為

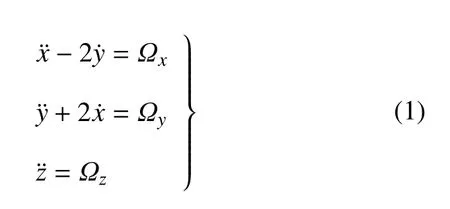
和

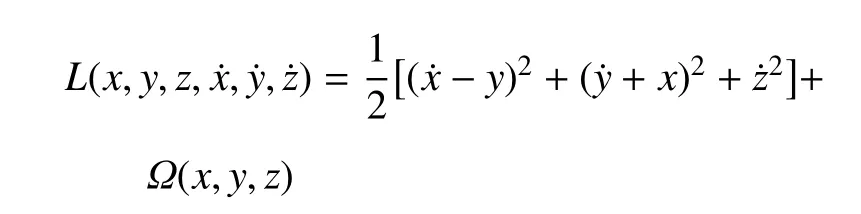
?(x,y,z)是系統的勢函數，通常表示為

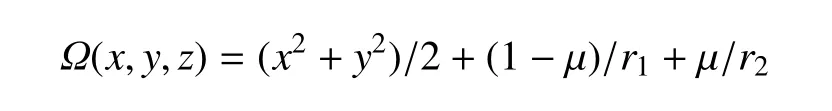
其中r1,r2分別表示航天器與P1,P2之間的距離

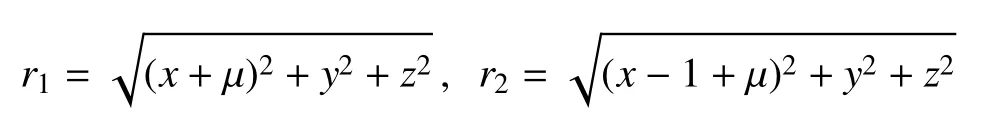
通過Legendre變換

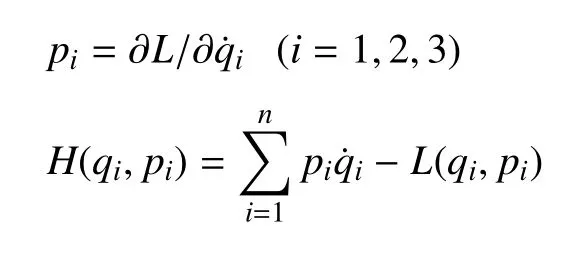
其中qi,pi(i=1,2,3)分別為航天器的坐標q=(x,y,z)和動量p=(px,py,pz)，可以得到圓型限制性三體問題的Hamilton函數

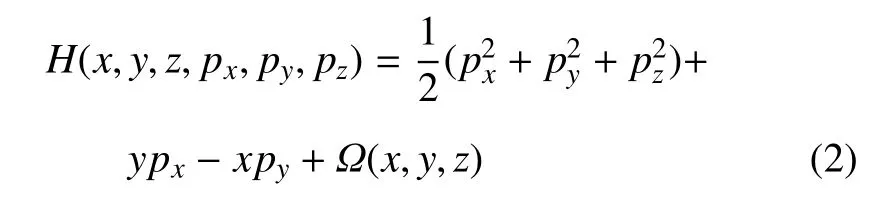
該系統具有雅可比能量積分

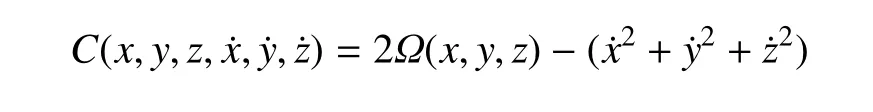
由Hamilton函數(2)，可推導出圓型限制性三體問題的正則方程為

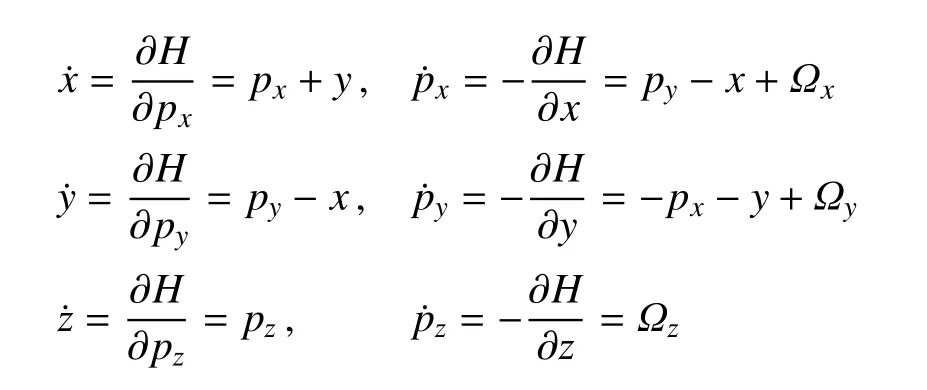
1.2 不變流形

不變流形是與平動點周期軌道光滑連接的一簇空間軌道，航天器在不變流形上可以無動力飛行.因此，不變流形可以作為低能軌道轉移的通道，在深空探測軌道轉移設計中有著重大應用價值.

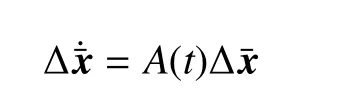
其中A(t)為系統(1)的雅可比矩陣，?ˉx為相對于不動點狀態的偏移量.由ˉx0點出發，積分一個周期后的狀態所對應的狀態轉移矩陣Φ(0,T)稱為單值矩陣[31].周期軌道上不同的點對應不同的單值矩陣，每個單值矩陣有一個不穩定特征根λs(λs＞1)及一個穩定特征根 λu=1/λs(λu＞ 1)，它們分別對應著特征向量和，它們包含了穩定流形和不穩定流形的方向信息.在點處沿特征向量方向增加一個微小狀態擾動，則可以得到不變流形的積分初值.對于不變流形的計算有

一般都采用數值積分來計算不變流形.不變流形計算的關鍵是獲得積分狀態初值，而此初值和Halo軌道上的點有密切關系.由于圓型限制性三體問題的強非線性使得微分方程組(1)的解對初始值十分敏感，可能較小的計算誤差都將導致不變流形的能量誤差巨大.辛算法因具有保能量的特點而受到廣泛關注，而顯式辛算法具有比隱式辛算法效率高的優勢，因此本文考慮利用含有三階導數項的力梯度辛算法來計算不變流形.力梯度辛算法是將Hamilton系統分解成動能T(p)(僅關于動量p=(px,py,pz)的正定二次函數)和勢能V(q)(關于坐標q=(x,y,z)的函數)兩個可積部分，然后分別求解.圓型限制性三體問題的Hamilton函數有多種分解形式，最簡單的是分解成類動能T(p)和勢能V(q)兩部分

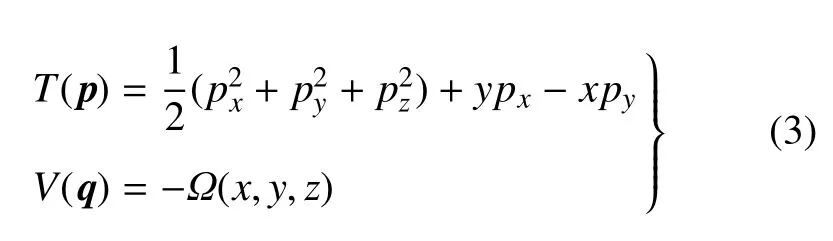
其中，ypx?xpy是由于Coriolis力的影響而產生的偏移部分.從式(3)可以看出，類動能T(p)不具有標準的二次型形式，因此從形式上看力梯度辛算法不適合求解圓型限制性三體問題.后文試圖通過改進算法來解決這一難題.

2 基于混合Lie算子的力梯度辛算法

考慮可以分解為動能T(p)和勢能V(q)的Hamilton系統

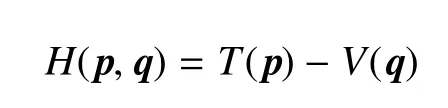
其中，動能T(p)僅僅是關于動量p的正定二次函數,即T(p)=p2/2，勢能V(q)是關于坐標q的函數.分別定義T(p)和V(q)的Lie算子[33-34]

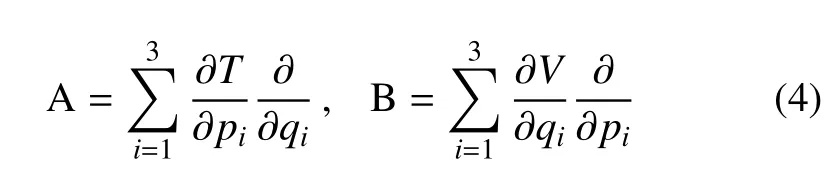
由于圓型限制性三體問題Hamilton函數分解中類動能T(p)不是動量p的標準二次型，因此具有形式(4)的Lie算子不再適用，考慮將類動能T(p)的Lie算子變為位置與動量的混合型算子

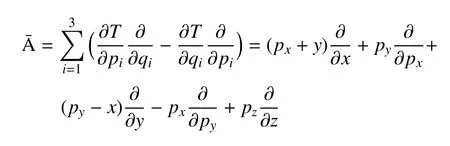
它作用于方程組(3)第一個方程的位置坐標和動量得到微分方程組

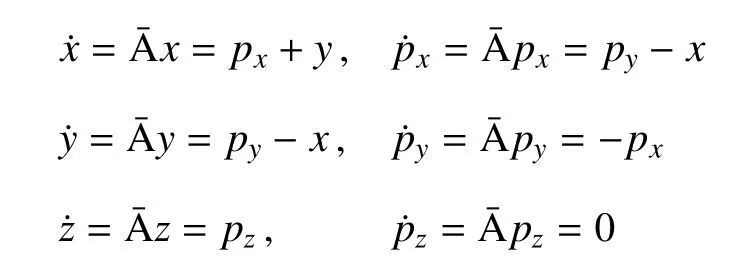
該方程組的分析解為

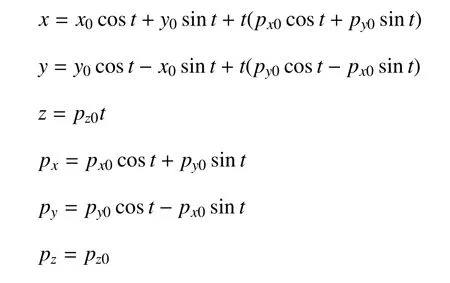
其中,(x0,y0,z0,px0,py0,pz0)為初始狀態，t是積分時間，于是新定義的混合算子ˉA可積，說明重新定義的混合Lie算子是合理的.容易驗證算子B也可積.

利用混合Lie算子ˉA和B構造復雜算子

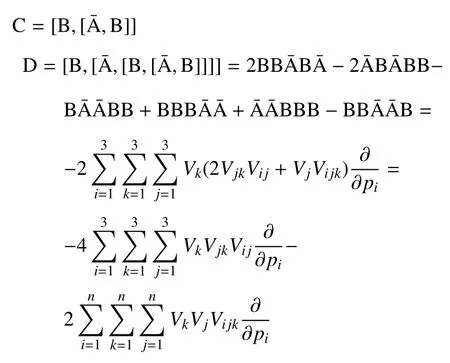
算子D是含有一階、二階和三階導數項的算子，可以與混合Lie算子ˉA和Lie算子B一起構造高階算法

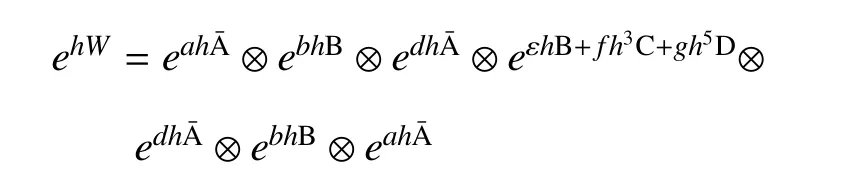
其中,h是積分步長，各積分系數分別為

其差分格式如下

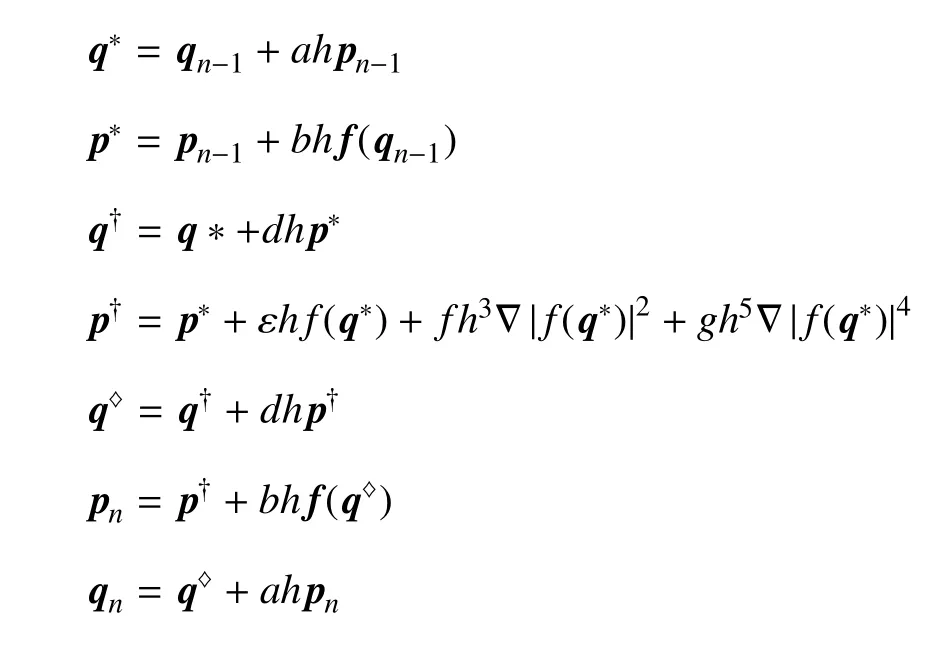
這里，力 f= ?V/?q.

由

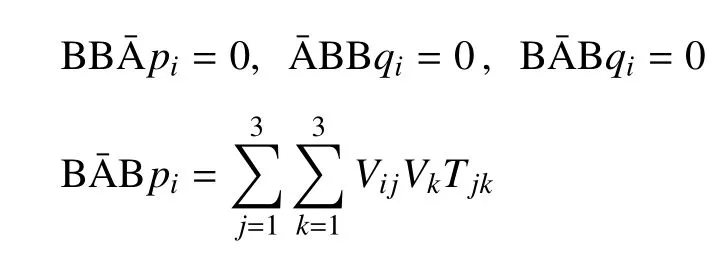
具體證明過程見附錄A,得到

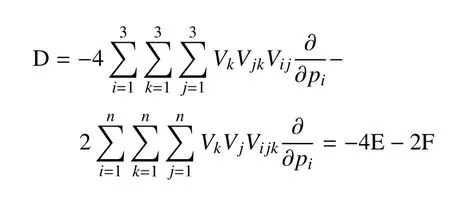
式中，E和F的具體表達形式見附錄B.這表明算子D是兩主天體的引力梯度，而不是旋轉坐標系所產生的非慣性力與主天體引力的混合梯度.

因此，通過引入混合Lie算子，分解成形式(3)的圓型限制性三體問題可以用改進的顯式辛算法進行求解.

3 仿真算例

仿真使用Matlab R2008b軟件，計算機為Windows 7系統，配置Intel(R)Core(TM)2 Duo CPU E7500處理器，主頻2.93 GHz，內存2.00GB，32位操作系統.利用第2節所得到的改進顯式辛算法MTGS研究地--月圓型限制性三體問題并與RK78和RK45法進行仿真對比，初始值參數如表1所示.

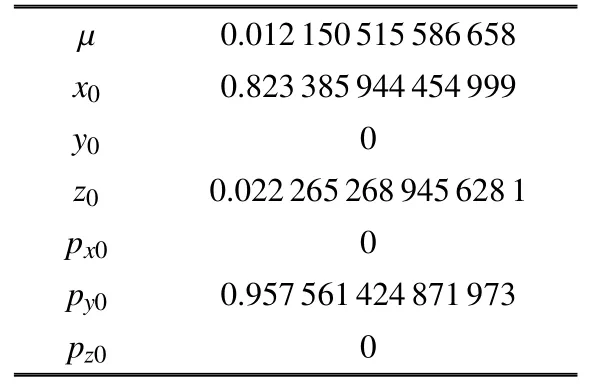
表1 初始值參數Table 1 The initial value of the parameter

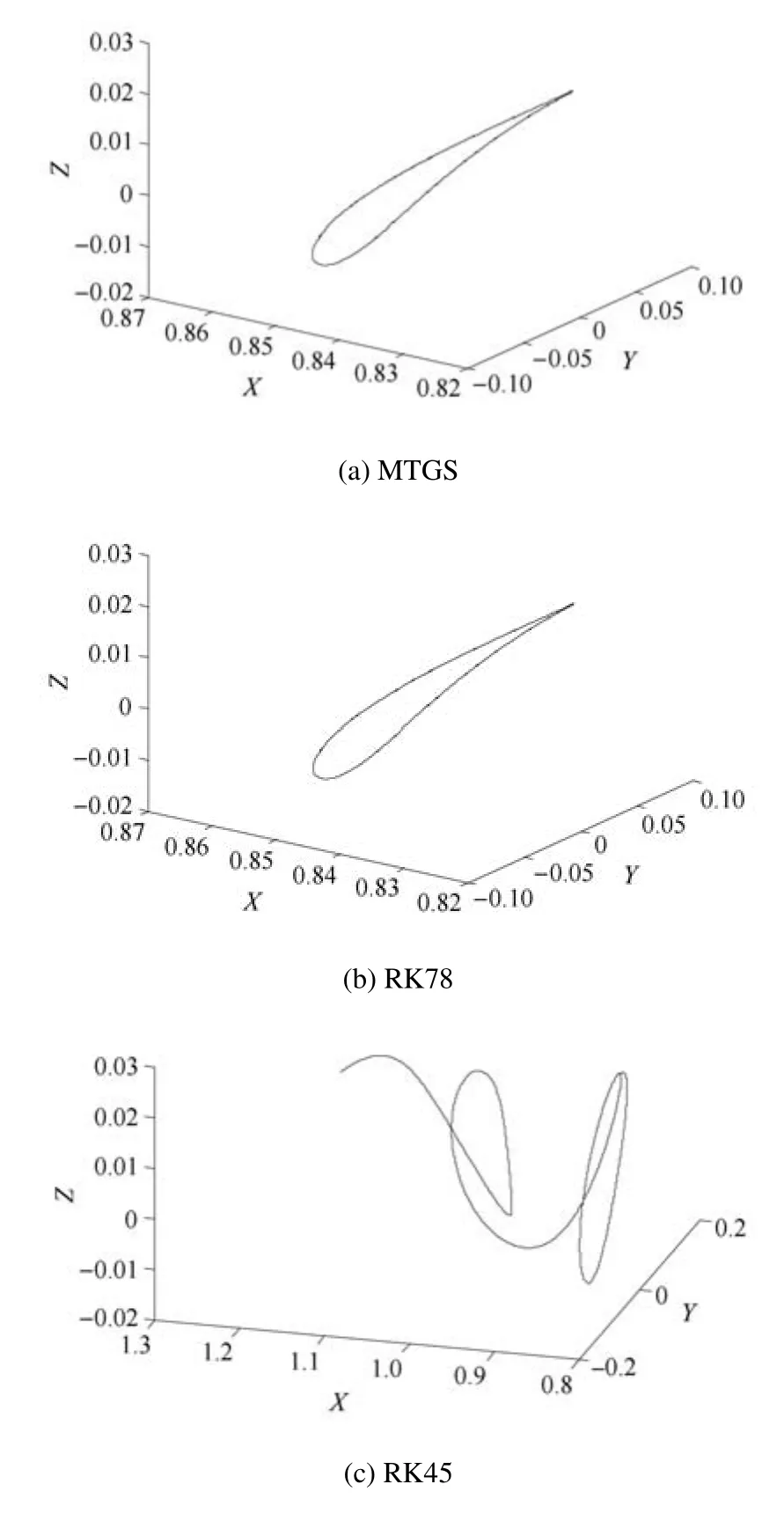
圖2 三種算法積分兩個周期得到的軌道Fig.2 The orbits of three algorithms integral two orbit periods

積分步長取0.001，積分兩個周期得到的軌道如圖2所示，可以看出本文改進的算法和RK78算法得到的軌道仍然能夠閉合，而通過RK45算法得到的軌道開始偏離周期軌道.當積分時長為3個周期時，軌道如圖3所示，改進的顯式辛算法、RK78算法與RK45算法都不能保證軌道閉合，RK45算法發散速度最快，改進的算法發散速度最慢.雖然Halo軌道產生偏移的快慢程度與其自身穩定性也有一定關系，但是，在同樣時間內，以同樣步長計算，不同算法發生偏移的快慢反映了算法的精確度.

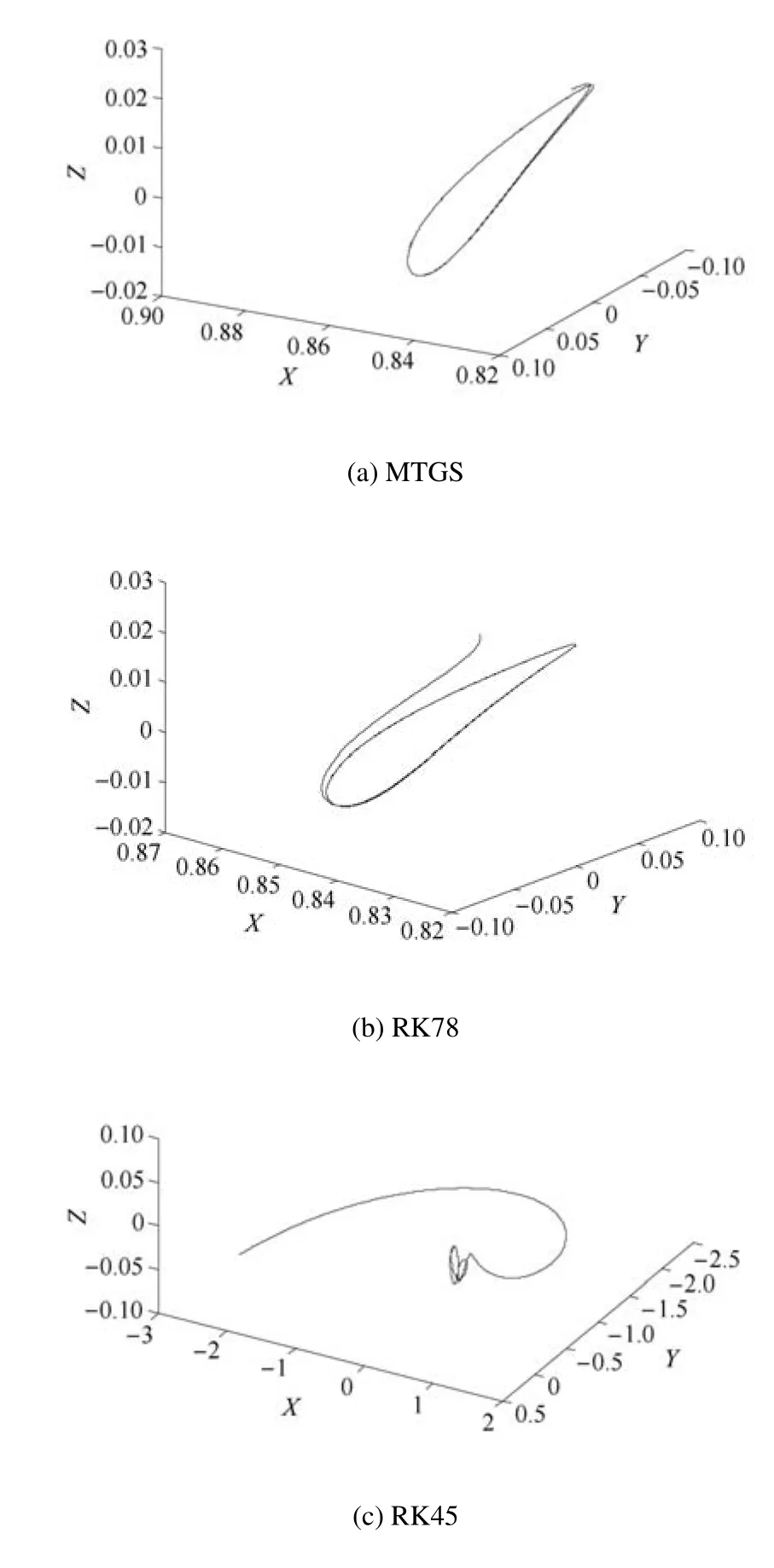
圖3 三種算法積分3個周期得到的軌道Fig.3 The orbits of three algorithms integral three orbit periods

積分100000步時絕對能量誤差如圖4所示，可以看出當步長取固定值0.001，積分100000步時改進的顯式辛算法的能量誤差最大為10?9量級.雖然RK78算法的初始能量誤差比較小，但隨著時間推移，能量誤差積累變得越來越大，出現驟增的情況，而RK45算法的能量誤差始終很大.與之相比，顯式辛算法的能量誤差始終保持在一定范圍內，能量誤差突然增大是因為航天器與主天體P2的距離突然變得非常小.

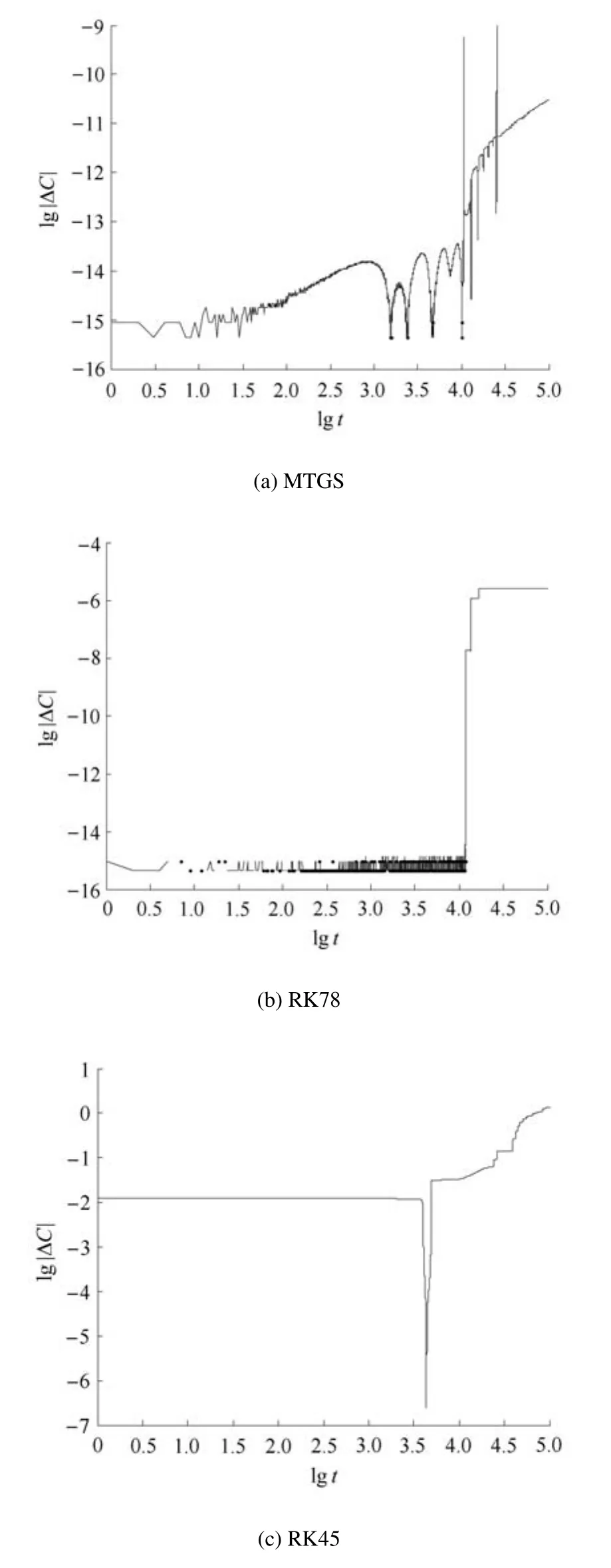
圖4 三個算法積分100000步的絕對能量誤差Fig.4 The absolute energy errors of 100000 steps with three algorithms

利用改進的顯式辛算法、RK78和RK45算法分別計算由表1所示初始參數得到的Halo軌道對應的一條不變流形，綜合考慮積分時間和積分精度，積分步長取0.0001，積分100000步時三種算法得到的穩定流形如圖5所示，不穩定流形與其關于y軸對稱，3種算法得到的不變流形從形狀來看差別無幾，但是不重合.從圖6所示能量相對誤差分析，可知利用改進的算法得到的不變流形，可以保證在長時間積分過程中能量誤差在很小范圍內，RK78算法初始能量誤差比較小，但呈增大趨勢，而RK45的能量誤差一直都很大.這3種算法所耗時長和相對能量誤差的最大值如表2所示，改進的顯式辛算法耗時最短，計算效率約是RK78的12.3084倍，且相對能量誤差的最大值最小，因此本文改進的顯式辛算法在低能軌道轉移過程中可以實現軌道拼接點精準能量匹配.

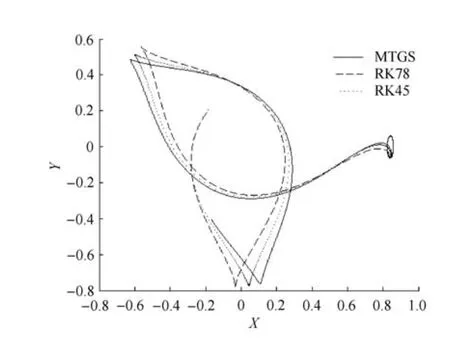
圖5 三種算法得到的一條穩定流形軌道Fig.5 Stable manifold of three algorithms

圖6 三種算法積分100000步的相對能量誤差Fig.6 The relative energy error of 100000 steps with three algorithms

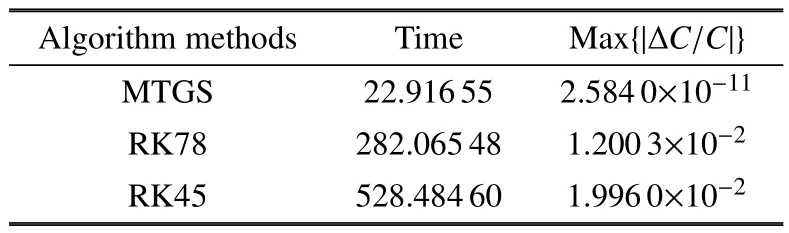
表2 三種算法的積分效率Table 2 Eefficiency of three algorithms

4 結論

在基于流形拼接法設計航天器低能轉移軌道的過程中，需要實時進行不變流形的能量計算.本文針對傳統數值積分能量耗散問題，研究了顯式辛算法在旋轉坐標系下的圓型限制性三體問題不變流形的保能量問題.顯式辛算法長時間積分時沒有長期的變化，能夠保持Hamilton系統的辛結構，本文通過改變圓型限制性三體問題分解形式中類動能(動能部分不是嚴格的正定二次型)Lie算子的形式，證明含有一階導數項、二階導數項和三階導數項的改進顯式辛算法可以求解旋轉坐標系下的圓型限制性三體問題，這也說明改進的Lie算子形式合理.最后，應用改進的顯式辛算法、RK78和RK45算法分別計算了地--月圓型限制性三體問題L1平動點附近的周期軌道和不變流形，并對其能量誤差和計算效率進行了分析.仿真結果顯示，本文改進的顯式辛算法在精度和能量誤差兩方面都具有較好的優勢.

1 Sezebehely V.Theory of Orbits:The Restricted Problem of Three Bodies.New York:Academic Press，1967

2劉林，侯錫云.深空探測器軌道力學.北京：電子工業出版社，2012(Liu Lin，Hou Xiyun.Orbital Mechanics of the Deep Space Probe.Beijing:Publishing House of Electronics Industry，2012(in Chinese))

3雷漢倫.平動點、不變流形及低能軌道.[博士論文].南京：南京大學，2015(Lei Hanlun.Equilibrium point，invariant manifold and low energy trajectory.[PhD Thesis].Nanjing:Nanjing University，2015(in Chinese))

4 Farquhar RW.The role of Sun-Earth collinear libration points in future space exploration//AAS Annual Meeting,1999

5 Dunham DW，Farquhar RW.Libration point missions，1978-2002//Libration Point Orbits and Applications.Singapore:World Scienti fi c,2003

6 Condon GL,Pearson DP.The role of humans in libration point missionswithspeci fi capplicationtoanEarth-Moonlibrationpointgateway station//AAS 01-307，AAS/AIAA Astrodynamics Specialist Coference,2001

7 Lo MW.The inter-planetary superhighway and the origins program//IEEE Aerospace Conference Proceedings，2002

8 Baoyin HX，McInnes CR.Solar sail Halo orbits at the Sun–Earth arti fi cial L1 point.Celestial Mechanics and Dynamical Astronomy,2006，94:155-17

9 Xu M.Application of Hamiltonian structure-preserving control to formation fl ying on a J2-perturbed mean circular orbit.Celestial Mechanics and Dynamical Astronomy,2012,113(4):403-433

10 G′omez G，Jorba A，Masdenmont J，et al.Study of the transfer from the Earth to a halo orbit around equilibrium point L1.Celestial Mechanics，1993，56:541-562

11袁建平,孫沖,方群.基于虛擬中心引力場方法的航天器轉移軌道設計.力學學報,2015,47(1):180-184(Yuan Jianping,Sun Chong,Fang Qun.Spacecraft’s transfer orbit design based on the virtual central gravity?eld method.Chinese Journal of Theoretical and Applied Mechanics,2015,47(1):180-184(in Chinese))

12賈建華,呂敬,王琪.帶脈沖的三維引力輔助變軌研究.力學學報,2016,48(2):437-446(Jia Jianhua,L¨u Jing,Wang Qi.Powered gravity assist in three dimensions.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):437-446(in Chinese))

13 Zhang RY，Luo JJ.Attainable sets approach for low-energy，lowthrustInterplanetarytransfers//InternationalAstronauticalCongress.Beijing，China,2013

14 Lei HL，Xu B，Hou XY，et al.High-order solutions around triangular libration points in the elliptic circular restricted three-body problem and applications to low energy transfers.Communications in nonlinear science and Numerical Simulation，2014，19:3374-3398

15 Lei HL，Xu B.High-order analytical solutions around triangular libration points in the circular restricted three-body problem.Monthly Notices of the Royal Astronomical Society，2013，434(2):1376-1386

16 Lei HL，Xu B，Hou XY，et al.High-order solutions of invariant manifolds associated with libration point in the elliptic circular restricted three-body system.Celestial Mechanics and Dynamical Astronomy，2013，117(4):349-384

17 Lei HL，Xu B.Analytiacl study on the motions around equilibrium points of restricted Four-body problem.Compute Nonlinear Science Number Simulat,2015，29:441-458

18 Dellnitz M，Junge O，Post M.On Target for venus:Set oriented computation of energy efficient low thrust trajectories.Celestial Mechanics and Dynamical Astronomy,2006，95:357-370

19 Howell K，Beckman M，Patterson C，et al.Representations of invariant manifolds for applications in three-body system//14th AAS/AIAA Space Flight Mechanics Conference，Maui，Hawaii，2004

20 Hsu CS.A theory of cell-to-cell mapping dynamical systems.Applied Mechanics，1980,147:931-939

21 Ruth RD．A Canonical integration technique.IEEE Transactions on Nuclear Science，1983，30：2669-2671

22李淵,鄧子辰,葉學華等.基于辛理論的載流碳納米管能帶分析.力學學報,2016,48(1):135-139(Li Yuan,Deng Zichen,Ye Xuehua,et al.Analysing the wave scattering in single-walled carbon nanotube conveying fl uid based on the symplectic theory.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1):135-139(in Chinese))

23 Pauli Pihajoki.Explicit methods in extended phase space for inseparable Hamiltonian problems.Celestial Mechanics and Dynamical Astronomy,2015，121:211-231

24 Liu L，Wu X,Huang GQ,et al.Higher order explicit symmetric integrators for inseparable forms of coordinates and momenta MNRAS459.MonthlyNoticesoftheRoyalAstronomicalSociety,2016 25 Hu WP，Deng ZC，Han SM，et al.Generalized multi-symplectic Integrators for a class of Hamiltonian nonlinear wave PDEs.Journal of Computational Physics，2013，235:394-406

26 Mei LJ，Wu X，Liu FY.On preference of Yoshida construction over Forest–Ruth fourth-order symplectic algorithm.The Europe Physical Journal C,2013,73:2413

27廖新浩，劉林.辛算法在限制性三體問題數值研究中的應用.計算物理，1995，12(1):102-108(Liao Xinhao，Liu Lin.Applications of symplectic algorithms to the numerical researches of restricted three-body problem.Physic Computation,1995，12(1):102-108(in Chinese))

28 Sun W，Wu X，Hang GQ.Symplectic integrators with potential derivatives to third order. Research in Astronomy and Astrophysics，2011，11:353-368

29 Hairer E，Wanner G.Solving Ordinary Di ff erential Equation.[s.l.]:Springer Verlag，1991

30李言俊，張科，呂梅柏等.利用拉格朗日點的深空探測技術.西安：西北工業大學出版社，2014(Li Yanjun，Zhang Ke，L¨u Meibo.et al.Deep Space Exploration Using Lagrange Equilibrium Point.Xi’an:Northwestern Polytechnical Chivesity Press,2014(in Chinese))

31 Bernelli-Zazzera F，Topputo F，Massari M.Assessment of Mission Design Including Utilization of Libration Points and Weak Stability Boundaries.[s.l.]:Politecnico di Milano，2004

32 G′omez G，Jorba A，Masdemont J，et al.Study re fi nement of semianalytical halo orbit theory.Final Report，ESOC Contract No:8625/89/D/MD(SC)，1991

33 Omelyan IP，Mryglod IM，Folk R.Optimized Forest-Ruth-and Suzuki-like algorithms for integration of motion in many-body systems.Computer Physics Communications,2002，146:188-202

34 Omelyan IP，Mryglod IM，Folk R.Symplectic analytically integrable decomposition algorithms:Classi fi cation，derivation,and application to molecular dynamics,quantum and celestial mechanics simulations.Computer Physics Communications，2003，151:272-314

COMPUTATION OF INVARIANT MANIFOLD BASED ON SYMPLECTIC ALGORITHM OF MIXED LIE OPERATOR1)

Zheng Dandan?,?Luo Jianjun?,?,2)Zhang Renyong??Liu Lei?,???(School of Astronautics，Northwestern Polytechnical University，Xi’an 710072，China)
?(National Key Laboratory of Aerospace of Flight Dynamics，Xi’an 710072，China)
??(Technology and Engineering Center for Space Utilization，Chinese Academy of Sciences，Beijing 100094，China)
??(Beijing Aerospace Control Center，Beijing 100094，China)

Invariant manifolds of periodic orbit near the libration points attract a lot of attentions due to their importance in the low-energy orbits transfer problem.In the process of low-energy orbit design,the energy of the invariant manifolds must be matched,but the energy is dissipated when integrating with traditional numerical integration method.The explicit symplectic algorithm with energy conservation is more efficient than the implicit symplectic algorithm,but it requires the Hamiltonian system to be divided into two integral parts,while the circular restricted three-body problem in the rotating coordinate system being inseparable.It is difficult to solve the circular restricted three-body problem in the rotating coordinate system by explicit symplectic algorithm.In this paper,the mixed Lie derivative operator of kinetic energy is used to solve the circular restricted three-body problem in the rotating coordinate system,and the e ff ectiveness of this explicit symplectic algorithm with the third derivation in dealing with this problem has been showed.Compared with the Runge-Kutta45 method and Runge-Kutta78 method,the symplectic algorithm with the third-order derivative term not only has high precision but also the smallest energy error and the highest efficiency.Finally,the invariant manifolds are calculated by the symplectic algorithm with the third derivative term,the patched point can match accurately with this method.

circular restricted three-body problem，invariant manifold，symplectic algorithm，mixed Lie operator

V412.4

A

10.6052/0459-1879-17-079

2017–01–11收稿，2017–07–18 錄用,2017–07–27 網絡版發表.

1)國家自然科學基金重大項目(61690210，61690211)和航天飛行動力學重點實驗室開放基金項目(2015afdl014,2015afd1017)資助.

2)羅建軍，教授，主要研究方向：航天飛行動力學與控制.E-mail:jjluo@nwpu.edu.cn

鄭丹丹,羅建軍,張仁勇,劉磊.基于混合Lie算子辛算法的不變流形計算.力學學報,2017,49(5):1126-1134

Zheng Dandan,Luo Jianjun,Zhang Renyong,Liu Lei.Computation of invariant manifold based on symplectic algorithm of mixed Lie operator.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1126-1134

附錄A

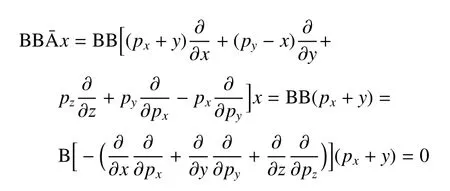
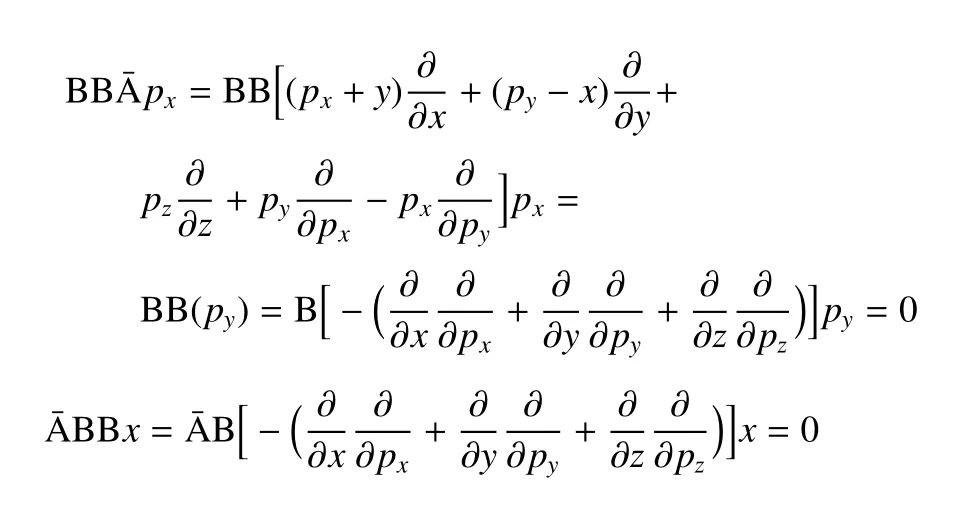
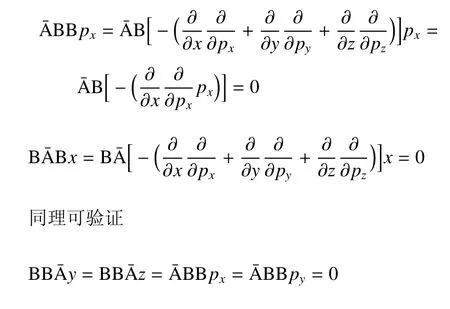
附錄B