基于經驗正交分解的聲速剖面場描述及研究
趙槊,金鑫,鄒定杰,李成鋼
(1.中海油田服務股份有限公司 物探事業部,天津 300451;2.深圳中海油服深水技術有限公司,深圳 518067)
基于經驗正交分解的聲速剖面場描述及研究
趙槊1,金鑫1,鄒定杰2,李成鋼2
(1.中海油田服務股份有限公司 物探事業部,天津 300451;2.深圳中海油服深水技術有限公司,深圳 518067)
本文研究了基于正交分解的聲速剖面場的構建原理及過程.并基于MATLAB平臺,對實測數據進行正交分解,得到特征值對應的特征向量,即經驗正交函數EOF.利用少數幾階EOF重構SSP,并與實測SSP對比,驗證了重構聲速剖面的可行性及精度問題.
聲速剖面;經驗正交分解;重構
在海洋領域應用中,獲得海洋水聲環境參數是非常必要的,而聲速剖面SSP(Sound Speed Profile)是其中最重要的參數之一.各種海洋水聲參數都會隨著時間和空間的變化而變化,由于受外界環境(如溫度、鹽度、密度、生物群等因素)的影響,SSP會發生較大的變化,特別是在淺水水域中.近年來在學術界中,對海水聲速以及影響聲速的溫度、鹽度、密度等因素進行著大量的測試和分析,試圖用數學模型描述海水聲速的變化規律.
聲速剖面測量有直接法和參數反演法.直接法往往采用CTD(Conductivity, Temperature, Depth)聲速儀直接測量或間接測量聲速剖面.但是,該方法難以快速測量大面積海域的聲速剖面,而是需要進行逐點測量,進而測量時間較長,且獲得聲速剖面具有明顯的局限性.而參數反演法監測聲速場,方法過于復雜,需有較深的聲學理論基礎,對海上作業人員來說相對較難.若能采用數學模型,運用描述聲速場的相關參數陣或參數,來進行聲速剖面場的變化的描述,得到與實際聲速剖面比較相符的聲速剖面,就可以彌補直接法和參數反演法的不足之處,增加工作效率,降低成本,也減輕了作業人員的理論學習負擔.
經驗正交函數(Empirical Orthogonal Functions,EOF)是描述SSP最有效的基函數,它能夠將SSP在時間和空間變化上分解,把聲速參數化,即分解為隨時間變化的SSP和隨深度變化的SSP.下文提出一種新的基于EOF描述SSP的方法,并利用實測數據基于MATLAB平臺進行正交分解,利用3階EOF來擬合SSP,與實測的SSP進行對比研究.
1 聲速剖面場構建原理
EOF分析方法是提取主要數據特征向量的一種方法,它能夠把隨時間/空間變化的變量分解為不隨時間/空間變化的空間函數,以及只依賴時間/空間變化的時間函數部分.基于EOF的SSP就是將聲速用正交時間函數和正交深度函數表示,并把聲速采樣地理坐標作為SSP的權重.
1.1 基于經驗正交函數的構建過程
假設一個采樣序列中有N個聲速剖面,因為采樣時受到外界條件的限制,不可能按等距離取樣,因此需插值法,插值得到等距離點處(其深度為)的聲速值,轉化到M個垂直標準層,得到聲速矩陣,記為.將聲速矩陣用平均聲速剖面與聲速擾動X來表示,即為,因此擾動X的協方差矩陣.求出此協方差矩陣的特征值矩陣λ和特征向量F,,其特征向量F就是所求的經驗正交函數.
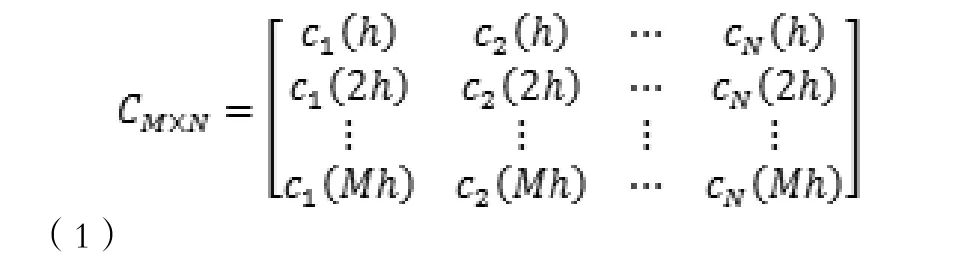

每條聲速剖面與平均聲速剖面之差,即為聲速撓動值x:
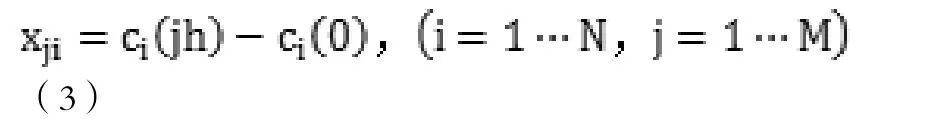

式中,λ為協方差矩陣的特征值,F為與特征值相對應的縱向量,即為特征向量.將特征值λ按大小排序,選取K個特征值較大所對應的特征向量,用該特征向量來表示聲速剖面,即所求經驗正交函數,則:
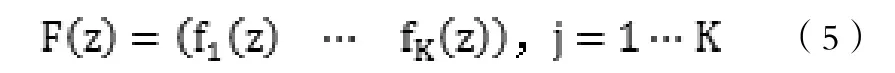
因此,重新構建的任意點聲速剖面表示為:
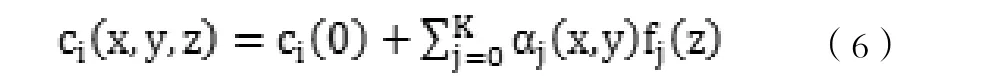
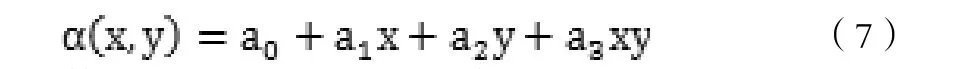
其中a0、a1、a2、a3是待求的參數.則:
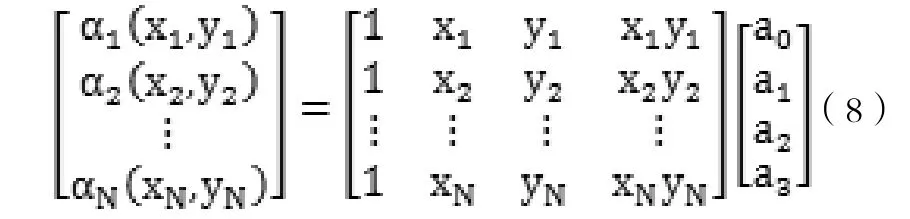
上式表示為:

所以,重新構建的任意點聲速剖面進一步表示為:

2.2 誤差計算
眾所周知,鹽度、壓力和水溫等是海洋聲速變化的主要影響因素,在不同的海域情況下,其影響各不相同.用公式(10)構建的聲速剖面,具有一定的經驗性,其解算出的SSP與實測SSP總會有一定的誤差,表示為:

為了衡量基于正交函數分解的聲速剖面的準確性,我們用均方根誤差的大小來表示:

3 試驗
在某海域中,使用CTD設備實測,共采樣25條聲速剖面數據,水深約45米左右.首先對測量的數據進行預處理,包括格式的轉換、插值解算等.然后,基于MATLAB系統平臺,建立聲速矩陣,得到協方差矩陣,求解特征值和特性向量(也即為所確定的EOF).再根據加權系數函數,確定出系數a0、a1、a2、a3參數.最后,根據公式(10)重新構造聲速剖面,表示出該區域內任意一點的聲速剖面.該數據組的EOF如圖1,其協方差矩陣的特征值按大小排列,如表1.

圖1 前五階EOF

表1 特征值
從表中看出,前3個特征值遠大于其他特征值.而第1階特征值較大,進一步說明,第一階包含了聲速剖面場的主要信息,其他階數是對聲速剖面場的細微描述.
我們使用前3階EOF來分別重構其中1條SSP,并與實測SSP對比.發現重構的SSP與實測的SSP十分相近,其均方根誤差RMS分別為0.35m/s(圖2).

圖2 重構的SSP
3 結語
基于EOF重構聲速剖面場,最大特征值對應的特征向量基本上包含了聲速剖面變化的主要信息,較小特征值對應的特征向量描述了聲速剖面的細微變化.
基于正交函數分解構建SSP,具有能快速、精確的重構SSP.由表1數據可以看出前3個特征值遠大于其他特征值,所以只需要少數幾階就可以達到重構SSP的目的.
前3階EOF重構的SSP與實測的SSP十分相近,誤差很小.用的階數越多,擬合的精度越好,針對不同的要求,選擇不同的階數.若精度滿足要求的情況下,利用EOF 重構聲速剖面場將會增加工作效率,降低作業成本。
TE54
A
1671-0711(2017)11(上)-0143-02

