基于高斯偽譜法的翼傘系統復雜多約束軌跡規劃

羅淑貞， 孫青林,*， 檀盼龍， 陶金， 賀應平， 羅浩文

1. 南開大學 計算機與控制工程學院， 天津 300380 2. 中航工業宇航救生裝備有限公司， 襄陽 441003 3. 河南科技大學 農業工程學院， 洛陽 471003

基于高斯偽譜法的翼傘系統復雜多約束軌跡規劃

羅淑貞1， 孫青林1,*， 檀盼龍1， 陶金1， 賀應平2， 羅浩文3

1. 南開大學 計算機與控制工程學院， 天津 300380 2. 中航工業宇航救生裝備有限公司， 襄陽 441003 3. 河南科技大學 農業工程學院， 洛陽 471003

翼傘系統在實際環境中飛行時易受到風場以及地形環境等復雜干擾的影響，無法精確歸航，控制難度較大。針對該問題，提出了一種針對復雜多約束條件的翼傘系統的最優控制軌跡規劃方法，可同時實現翼傘系統在復雜環境下逆風對準、精確著陸以及控制量全局最優的控制目標。首先，建立了風場干擾下的翼傘系統模型; 然后，通過引入地形環境曲面，將復雜環境轉化為實時路徑約束，將軌跡著陸偏差以及逆風雀降轉化為終端約束，并考慮控制量消耗最小為目標函數，以此將復雜環境下的翼傘系統的軌跡優化轉化為一系列非線性的帶有復雜約束的最優控制問題；最后，采用高斯偽譜法將多約束最優控制問題轉化為易于求解的非線性規劃問題。通過設立3組復雜環境仿真實例和實驗驗證，表明本文方法使翼傘系統在多種較惡劣的復雜環境中有效應對多類約束條件，規劃出控制量全局最優的可行軌跡。與已有的混沌粒子群優化算法相比，本文方法具有較好的最優性和較高的精度。

翼傘系統； 復雜多約束； 高斯偽譜法； 最優控制； 軌跡規劃

近年來，翼傘系統在軍事、航天救災或民用領域中得到了迅速發展和廣泛應用[1-5]。由于翼傘是利用沖壓空氣來保持一定形狀的柔性飛行器，易受到陣風、雨、山峰區或氣象禁飛區等復雜環境的影響，不能實現精確歸航。因此，研究翼傘系統在復雜環境下的軌跡優化問題具有現實意義與廣泛應用價值。目前，針對翼傘系統進行軌跡規劃的方法主要有最優控制法和智能優化算法。其中，最優控制法包括間接法和直接法。Rademacher等[6]應用最優控制法對翼傘系統進行了在線軌跡規劃，并考慮了翼傘著陸時刻的轉彎角。Cleminson[7]采用動態規劃方法，求解了翼傘系統基于運動模型的軌跡規劃問題。國內比較有代表性的成果是：熊菁[8]采用間接法-共軛梯度法對翼傘系統的最優控制問題進行了求解，缺點是針對初值估計要求高，需要求解狀態方程和協態方程，過程較繁瑣。目前，多采用對初值敏感度低、收斂半徑大的直接法進行軌跡優化，偽譜法就是一類典型的直接法[9-13]。Elnagar等[9]首次利用偽譜法將最優控制問題轉化為非線性規劃問題。文獻[10]證明了高斯偽譜法較其他算法具有精度高、收斂速度快的優勢。Zhang等[12]運用偽譜法完成了翼傘系統歸航軌跡容錯的設計。還有一類代表性成果是利用智能優化算法進行求解。焦亮[13]、陶金[14]等分別使用粒子群優化算法、量子遺傳算法對翼傘系統的歸航軌跡進行了優化。謝亞榮等[15]采用粒子群優化算法針對翼傘系統處于地形威脅環境下進行了軌跡規劃，這類智能優化算法收斂速度較快，在工程優化等諸多領域得到了廣泛應用，但其在求解復雜約束問題時算法實現較復雜，全局搜索能力欠佳，易發生早熟收斂[16-19]。

與上述研究成果不同的是，本文通過建立翼傘系統在風場中的運動模型，考慮翼傘系統在復雜環境飛行時受到的初值約束、控制約束、實時路徑約束等復雜約束條件，構造出以控制量為優化目標的最優控制問題；采用高斯偽譜法將該優化問題轉化為易于求解的非線性規劃問題，從而求出最優飛行軌跡；通過多組仿真與實驗，可知不同初始狀態下的翼傘系統均可滿足各種復雜約束條件，得到的最優軌跡平滑合理、便于跟蹤，保證了翼傘系統對外界復雜干擾的穩定性和魯棒性。與已有的混沌粒子群優化算法分析比較，本文方法尋優速度較快，精度更高。

1 復雜環境下翼傘系統的問題描述

1.1 基于風場下的翼傘系統模型

對飛行器進行軌跡規劃時，為了解其飛行軌跡以及性能，通常都采用簡單模型[1,3-5]。由于翼傘系統是一個復雜度較高的非線性系統，其控制是通過操縱傘翼后緣左右兩側的傘繩來實現。本文通過對文獻[5]建立的六自由度模型進行仿真，得到了翼傘系統雙側、單側下偏與滑翔比、垂直速度的關系，并在此基礎上建立了翼傘系統的質點模型。仿真結果如表1和表2所示。

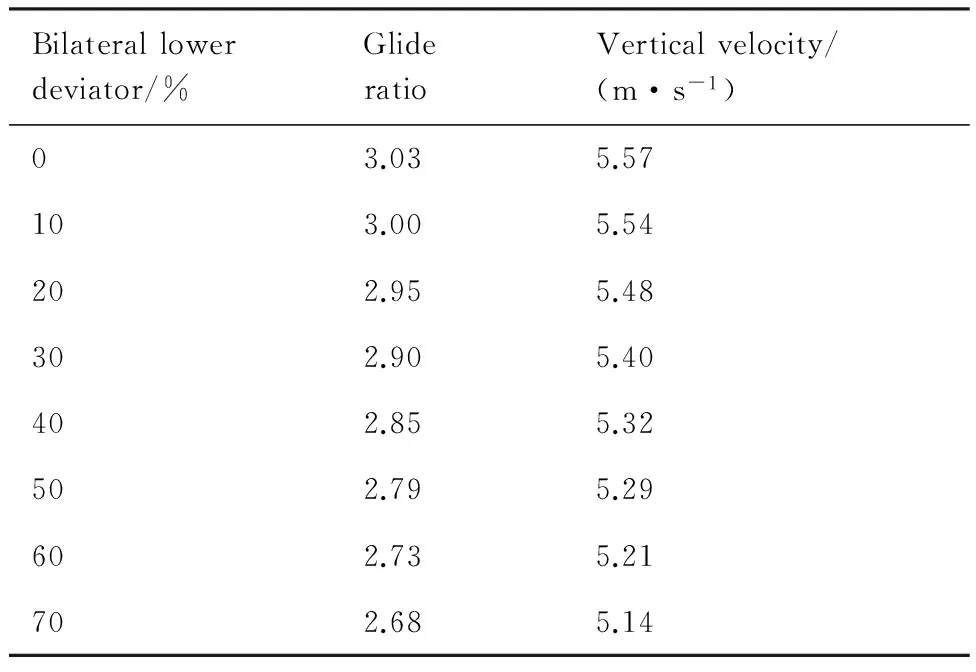
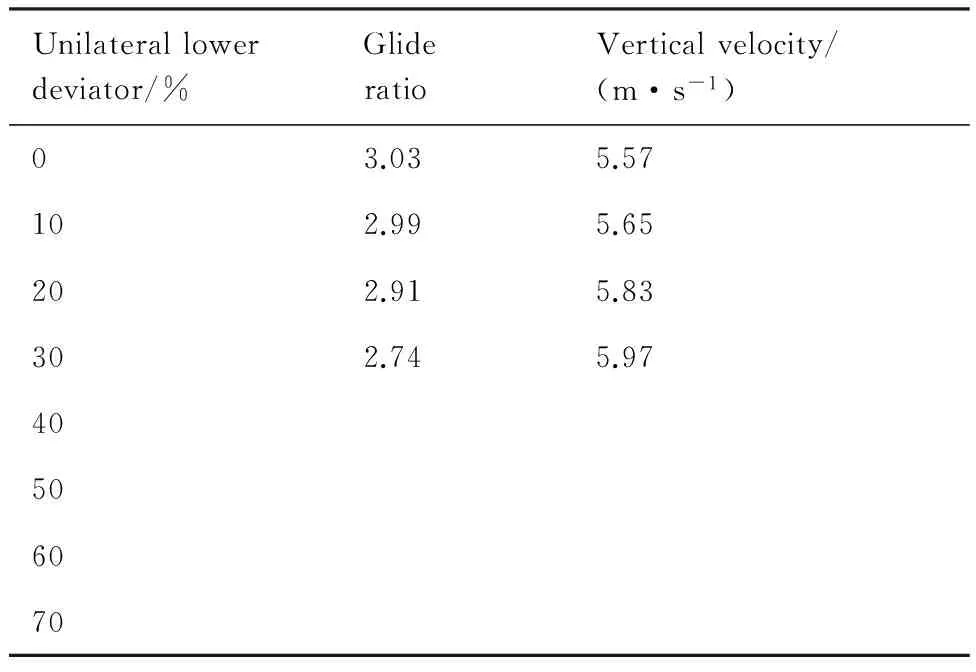
如表1所示，隨著雙側下偏量的增大，垂直速度和系統的滑翔比均有小量的減少。采用調節下偏量的方式控制翼傘系統縱向面的軌跡是不理想的，且下拉操縱繩的距離較大，導致控制難度增大，軌跡的傾角變化很小。如表2所示，當單側下偏量增大時，對系統的滑翔比以及垂直速度影響較小，且滑翔比的降低不利于系統的抗擾性，垂直速度的增大也不利于系統的滑翔和對滯空時間的預測，同時大的下偏量控制提高了對執行機構的要求。因此為了保持系統的穩定性，防止系統失速，單側下偏量往往被限制在一定的范圍內。由上述分析可知，在一定下偏量范圍內，穩定飛行時翼傘的滑翔比和飛行速度基本可看作常數。因此為了簡化模型，做以下假設[4-7]：

表1 雙側下偏量對翼傘系統的影響

Table 1 Influence of bilateral lower deviator on parafoil system

Bilaterallowerdeviator/%GlideratioVerticalvelocity/(m·s-1)03.035.57103.005.54202.955.48302.905.40402.855.32502.795.29602.735.21702.685.14

表2 單側下偏量對翼傘系統的影響

Table 2 Influence of unilateral lower deviator on parafoil system

Unilaterallowerdeviator/%GlideratioVerticalvelocity/(m·s-1)03.035.57102.995.65202.915.83302.745.9740506070

1) 當翼傘完全充滿后穩定飛行時，翼傘系統的垂直下降速度和水平飛行速度保持不變。

2) 風場已知。

3) 系統對控制輸入的響應無延遲。

本文的坐標系選取平面大地系，目標點為坐標系原點，翼傘系統的運動方程如下：

(1)

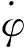
風場主要包括常值風、陣風、紊流等類型，在針對不同情況時可選擇不同類型的風場。當地形環境比較平坦時，常值風對翼傘系統飛行軌跡的影響較大；當地形環境較惡劣，存在山峰區等約束時，翼傘系統易受到風速變化迅速、較惡劣的突風干擾。

1.2 復雜環境下的約束條件

1) 初值約束

初始時刻t0已知，則初始狀態信息可以表示為

(2)

2) 終端約束

選定坐標原點為目標點，終端時刻tf固定，并將著陸位置偏差作為終端約束進行處理，這樣可使翼傘系統以高精度降落到目標點，即

(3)

當降落高度選擇適當，且為逆風滑翔的情況下，可使落地速度降到極小值，因此必須使翼傘在著陸階段逆風對準，β為方向角，將這一條件轉化為終端約束，則最后階段的著陸角為

φ(tf)=β±(2n+1)πn=0,1,…

(4)

3) 控制約束

u允許的最大控制量umax對應的是最小轉彎半徑。由于本文水平速度vs=15 m/s，最小轉彎半徑為100 m，則本文中控制量最大值umax=0.15。

|u|≤umax

(5)

4) 實時路徑約束

在飛行當中遇到的不利地形環境通常包括山峰區、禁飛區等。為了保證其安全性，飛行時須躲避這些威脅環境。本文對山峰區、禁飛區引入一個地形環境曲面，可表示為下述模型：

(6)

(7)

式中：Rp為最大半徑；h0為高度；δ為曲面光滑系數；p為山峰區或禁飛區的個數。

該模型投影到x-y平面上是以(xp,yp)為圓心的一系列同心圓。則翼傘系統針對地形環境惡劣時需要滿足的實時路徑約束條件為

(8)

1.3 目標函數

考慮控制量消耗最小這一目標函數，即求解最優控制u使下述目標函數最小：

(9)

翼傘系統同時滿足運動方程約束式(1)、初值約束式(2)～式(4)、控制約束式(5)和實時路徑約束式(8)。

因此，復雜環境下翼傘系統的軌跡優化問題轉化為一類非線性的帶有復雜約束的最優控制問題。本文通過高斯偽譜法對優化問題進行轉化，將問題轉化為具有代數約束的非線性規劃問題，并利用序列二次規劃算法進行求解。

2 高斯偽譜法求解最優軌跡

2.1 狀態變量和控制變量離散

高斯偽譜法的離散點分布在[-1,1]，因此需要將第1節的問題的時間區間[t0,tf]轉換為[-1,1]，引用時間變量τ做以下變換：

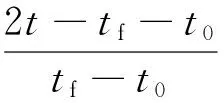
(10)

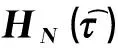
(11)

由于本文的最優控制問題含有初值約束和終端約束，因此還需要再引入2個節點，τ0代表初始時刻，τf=τN+1=1代表終端時刻。所以一共有N+2個LG配點{τ0,τ1,…,τk,…，τN+1}。

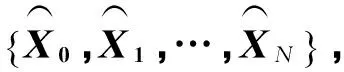
(12)

(13)

將控制變量在屬于開區間(-1,1)上的N個LG配點處離散，得到一組N個離散變量，再通過Lagrange插值多項式近似得到u(τ)。

(14)

(15)

2.2 終端約束和控制約束

從式(12)中可以看出，近似的x(τ)只是對應前N+1個節點, 沒有終端狀態，而相對應的u(τ)沒有初始和終端時刻的控制量。

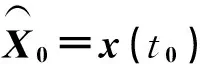
(16)

將式(16)中的積分運算也離散化，可得到

k=1,2,…,N

(17)

式中：?k為積分權重因子，可通過對插值基函數進行積分計算得到。

本文對初始時刻和終端時刻的控制量，由式(14)延伸得到，即

(18)

(19)

2.3 質點模型的運動方程轉化

將系統的運動方程轉化為對插值基函數的求導運算。對式(12)進行求導得到

(20)

對Lagrange多項式在節點τk處進行求導得到一個微分矩陣，即

k=1,2,…,N,i=0,1,…,N

(21)

從而得出狀態變量對時間的導數為

(22)

又因為運動方程經離散后得到

(23)

從而運動方程可由如下代數方程代替：

k=1,2,…,N

(24)

2.4 實時路徑約束和目標函數離散化

將實時路徑約束在節點τk處離散化，得到

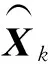
(25)

將目標函數在節點τk處做離散處理，積分項用數值積分求解，可得到以下形式:

(26)

經過以上轉化，可把在復雜環境下的翼傘軌跡優化問題轉化為一系列非線性參數優化問題，對其采用序列二次規劃算法進行求解，離散計算出控制量最優的飛行軌跡，由于通過高斯偽譜法解算出一系列代數約束方程，則首先選用少量節點對該優化問題進行求解，快速得出一條軌跡后通過對該軌跡進行插值從而得到更多的節點，以此獲得更高精度的軌跡。

3 仿真與實驗

為驗證本文方法的可行性，給出了仿真與實驗結果。首先，利用MATLAB及其相關工具箱，設計3組復雜環境仿真實例，并按照本文方法離線計算出控制最優的翼傘系統軌跡；然后，將本文方法與現有的混沌粒子群優化算法進行對比驗證；最后，將本文方法所構造的最優控制軌跡在翼傘系統的半實物仿真平臺上進行實驗驗證。

3.1 仿真條件

作為仿真實例，選用空投質量為80 kg的傘型, 展弦比為1.73，傘繩和吊帶長度分別為3.7 m 和0.5 m，傘衣面積為22 m2，空投物阻力特征面積為0.5 m2。根據所選傘型及其六自由度仿真結果，在保證翼傘傾斜角小于20° 的前提下，翼傘系統的運動參數為：水平速度為vs=15 m/s，垂直速度為vz=5 m/s，終端時刻tf=z0/vz。設定3組仿真情形：① 常值風場，地形環境平坦。設置翼傘系統處于一種初始狀態下，分析受到不同風速影響的情況。② 地形環境惡劣。③ 突風風場，地形環境惡劣。情形2和情形3設定翼傘系統分別在3種初始狀態下進行運動。情形2是在只針對處于不利地形環境下的仿真，情形3則是在針對當翼傘系統處在不利地形環境的情況下，并且受到突風干擾的影響，因此設置情形3 的初始狀態和地形環境同情形2。3種情形下的初始狀態如表3所示。

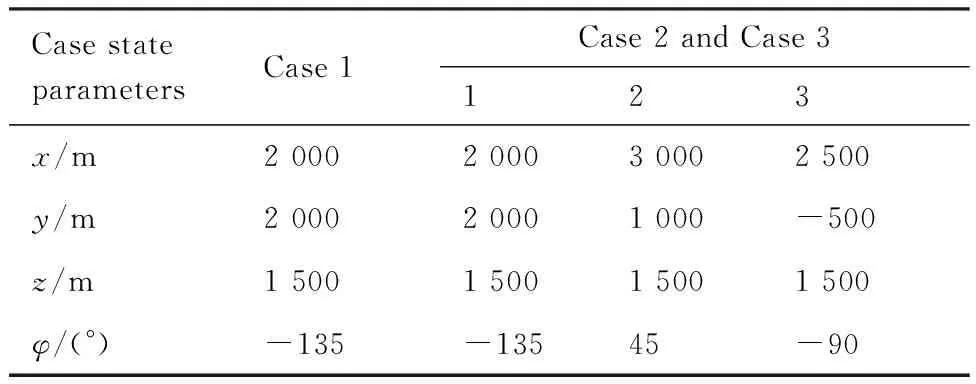
表3 初始狀態Table 3 Initial states

3.2 仿真驗證及分析

1) 情形1

當地形環境較平坦，翼傘系統受到常值風干擾的影響較大，設定風向為x軸正向，初始值設置如表1所示。風速vwind為0、2、4 m/s下翼傘系統在x-y平面的飛行軌跡如圖1所示。可見，翼傘系統的軌跡呈現規律性。先進行一段時間的滑翔快速靠近目標點，隨后調整轉彎角度進行逆風對準。由于翼傘系統承受逆風作用，隨著風速的增大，系統的水平速度減小，但飛行時間固定，則總飛行路程減小。對應風速下的翼傘系統控制曲線如圖2所示。系統在滑翔階段的控制量為零，在逆風對準階段的控制量隨之增大，且整個飛行過程中的控制量小于所設定的控制約束范圍。

風速為4 m/s時的三維航跡如圖3所示，規劃出的最優軌跡可精確著陸，軌跡連續、平滑，易于跟蹤控制。3種情況下的仿真結果如表4所示。可知，3種風速下的軌跡均能精確達到目標點，著陸角實現逆風對準，隨著風速的增大，總控制量隨之增大。

2) 情形2

初始狀態同情形1。施加4個山峰區環境約束，高度均為2 000 m，在水平面的投影分別是以距離目標點較遠的(2 200,1 300) m，(1 000,1 500) m和距離目標點較近的(500,500) m，(1 500,0) m為圓心的一系列同心圓，最大半徑均為400 m。不同初始狀態下翼傘系統在水平面的軌跡如圖4所示。當初始狀態為1時，初始飛行角為-135°，翼傘系統先進行滑翔靠近目標點，當遇到山峰區時，翼傘系統根據此時的高度實時判斷出當前的可行區域，從而穿越山峰，到達目標點。由圖4可知，不同初始狀態下的翼傘系統可實時躲避密集山峰區，在終端時刻精確到達目標點。

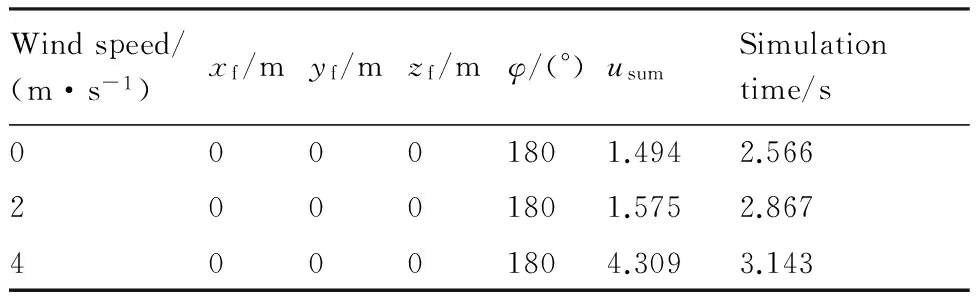
Windspeed/(m·s-1)xf/myf/mzf/mφ/(°)usumSimulationtime/s00001801.4942.56620001801.5752.86740001804.3093.143

3種初始狀態所對應的控制曲線如圖5所示。可見，3種初始狀態下的最優控制量類似余弦曲線，且整個過程中的控制量相對于設定的控制約束范圍較小。圖6為初始狀態為1時的翼傘系統三維軌跡。

情形2的仿真結果如表5所示。可知，當在不利地形環境下飛行時，處于不同初始狀態下的翼傘系統均能精確、逆風到達目標點且控制量達到最優。

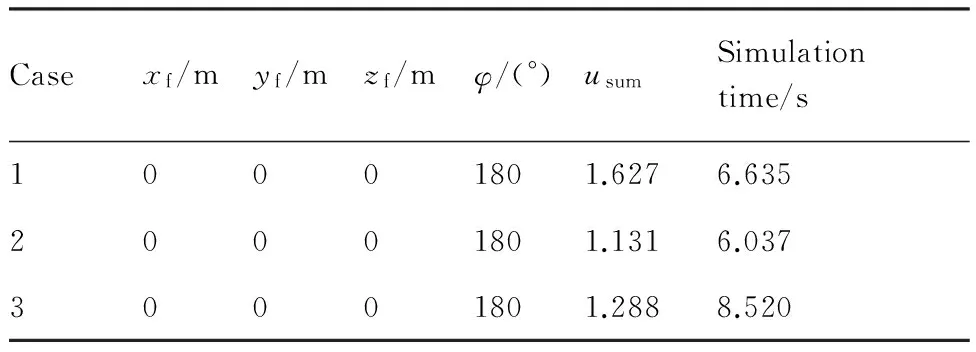
Casexf/myf/mzf/mφ/(°)usumSimulationtime/s10001801.6276.63520001801.1316.03730001801.2888.520

3) 情形3

初始狀態以及地形環境同情形2。由于在地形環境惡劣時，翼傘系統相對來說受到風速變化迅速，較惡劣的突風作用更切合實際。選擇NASA經典突風模型[20]，如式(27)所示,vwind為風速，并設定最大風速為vmax=4 m/s，方向為x軸正向，作用在整個飛行過程中。

(27)

翼傘系統處于惡劣地形環境時的仿真結果如圖7～圖9所示。由圖7可見，在突風作用下翼傘系統水平速度降低，飛行總路程縮短，得到的最優軌跡可以實時躲避山峰區，完成逆風對準著陸。

3種初始狀態所對應的控制量如圖8所示。3種初始狀態下的控制曲線趨于規律性，在轉彎處控制量增大，隨后趨于穩定，保證了翼傘系統飛行過程中的穩定性。圖9為初始狀態為1時的三維軌跡。可見，在突風的影響下，翼傘系統可實時躲避山峰區，逆風著陸。

情形3的仿真結果由表6給出。可知，在3種初始狀態下的翼傘系統在突風作用下，實時躲避不利地形，控制量達到全局最優。

表6 情形3的仿真結果Table 6 Simulation results of example 3

通過設立3組仿真實例，詳細分析了翼傘系統在受到多種復雜約束下的飛行軌跡和控制量，結果表明，本文方法可使翼傘系統在多種較惡劣的復雜環境中有效應對多類約束條件，規劃出控制量全局最優的可行軌跡。由于在MATLAB環境下進行仿真，每條軌跡規劃時間均在9 s以內，滿足翼傘系統歸航需求。

3.3 對比驗證

為驗證本文方法的優勢，將文獻[11]中的混沌粒子群優化算法仿真結果與本文方法做比較，在有常值風2 m/s的環境下，風向為沿x軸正向，初始值為 (-3 500,-3 500,2 000) m，起始飛行角度為60°。水平面的軌跡以及性能指標對比如圖10和表7所示。

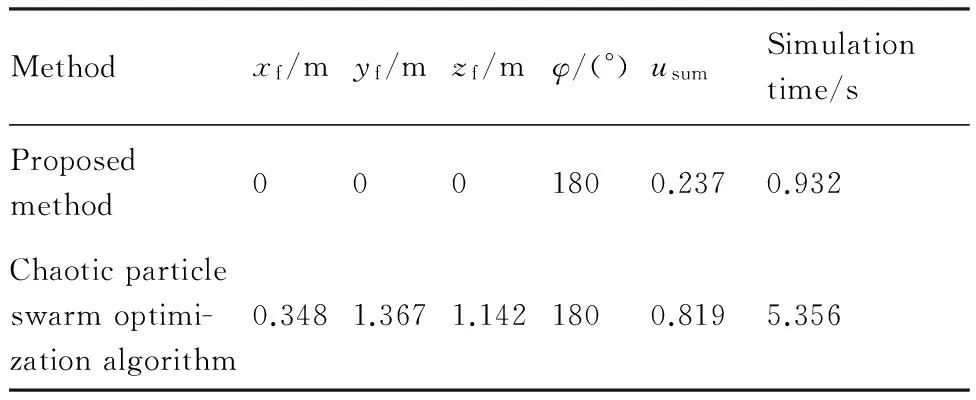
Methodxf/myf/mzf/mφ/(°)usumSimulationtime/sProposedmethod0001800.2370.932Chaoticparticleswarmoptimi-zationalgorithm0.3481.3671.1421800.8195.356

由對比結果可知，本文方法較混沌粒子群優化算法得到的軌跡更利于軌跡跟蹤與控制，精度較高，全局控制量以及尋優速度較好。

3.4 實驗驗證及分析

為進一步驗證本文方法的可行性，將所規劃的軌跡在翼傘系統半實物仿真平臺上進行驗證。翼傘系統的半實物仿真平臺[21]是一種對翼傘系統歸航控制器的控制性能進行分析和驗證的實驗平臺，通過建立翼傘系統的數學模型，仿真翼傘系統在實物歸航控制序列的作用下的動態響應，并實時顯示翼傘系統模型的位置、速度等信息。設定初始值為(1 500,1 500,1 160) m,vs=12.1 m/s，vz=2.9 m/s, 風向為沿x軸正向，風速為2 m/s, 本文方法的軌跡規劃驗證流程如圖11所示。由于實際的翼傘系統的單側下偏量與轉彎半徑負相關，下偏量越大，則轉彎半徑越小，在實際應用中根據控制量與單側下偏控制量的關系，將本文方法得到的控制序列轉化為實際系統對應的下偏操縱控制量作為控制輸入到實際八自由度翼傘系統模型，從而計算實際系統的軌跡。控制量對應的下偏操縱控制量和翼傘系統在下偏控制量作用下的軌跡如圖12和圖13 所示。

由于在實際翼傘系統中，其相對水平速度和垂直速度隨著下偏控制量的不同有小范圍變化，加上操縱機構執行時間的影響，在歸航過程中必然會產生偏差。如圖13所示，規劃的軌跡與實際系統軌跡的形狀與趨勢大致相同，且逆風對準的著陸目標也基本完成。由于受到下偏操縱量以及外界干擾的影響出現了累積誤差，最終導致規劃的軌跡與目標點之間的距離誤差為50.9 m。一般來說，實驗結果與仿真結果均存在一定程度上的區別，因此通過仿真與實驗均驗證了本文方法可以實現較好的控制效果。

4 結 論

本文將翼傘系統在復雜多約束下的軌跡優化轉化為一類帶有非線性約束的最優控制問題。

1) 通過建立在風場作用下的翼傘系統模型，并引入地形環境曲面，將復雜地形環境轉化為實時路徑約束，將軌跡著陸位置偏差以及逆風對準則轉化為終端約束，并考慮控制量消耗最小為目標函數。

2) 采用高斯偽譜法中對此問題進行轉化，并利用序列二次規劃算法進行求解。

3) 通過設計3組復雜環境仿真實例，詳細分析了在變化風場以及不利地形環境等不同初始狀態翼傘系統的軌跡以及控制量。

4) 通過與已有的混沌粒子群優化算法進行仿真對比，驗證了本文方法的最優性和時效性，并將其在半實物實驗平臺上進行實驗，得到的軌跡更利于軌跡跟蹤及控制。

本文提出的復雜多約束下的最優控制軌跡規劃策略可使翼傘系統有效應對多類約束條件，并實現全局控制最優，仿真與實驗均驗證了本文方法的可行性，為復雜環境下翼傘系統進行軌跡跟蹤控制提供一種新思路，未來的工作中會考慮為翼傘系統設計精確的閉環軌跡跟蹤控制器，以減少其對外界干擾的魯棒性和著陸誤差。

[1] OLEG A Y. Precision aerial delivery systems: Modeling, dynamics, and control[M]. Reston: AIAA, 2015: 3-8.

[2] GOCKEL W. Concept studies of an autonomous of GNC system for gliding parachute: AIAA-1997-1465[R]. Reston: AIAA, 1997.

[3] BABU A V S, SUJA V C, REDDY C V. Three dimensional trajectory optimization of a homing parafoil[J]. IFAC Proceedings Volumes, 2014, 47(1): 847-854.

[4] 梁海燕, 任志剛, 許超， 等. 翼傘系統最優歸航軌跡設計的敏感度分析方法[J]. 控制理論與應用, 2015, 32(8): 1004-1005. LIANG H Y, REN Z G, XU C, et al. Optimal homing trajectory design for parafoil systems using sensitivity analysis approach[J]. Control Theory & Applications, 2015, 32(8): 1004-1005 (in Chinese).

[5] JIAO L, SUN Q L, KANG X F, et al. Autonomous homing of parafoil and payload system based on ADRC[J]. Journal of Control Engineering and Applied Informatics, 2011, 13(3): 25-31.

[6] RADEMACHER B J, LU P, STRAHAN A L, et al. In-flight trajectory planning and guidance for autonomous parafoils[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(6): 1697-1712.

[7] CLEMINSON J R. Path planning for autonomously-guided parafoils: A dynamic programming approach[C]//Aerodynamic Decelerator Systems Technology Conferences. Reston: AIAA, 2013: 1346.

[8] 熊菁. 翼傘系統動力學與歸航方案研究[D]. 長沙：國防科學技術大學, 2005: 72-79. XIONG J. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005: 72-79 (in Chinese).

[9] ELNAGAR G, KAZEMI M A, RAZZAGHI M. The pseudo-spectral Legendre method for discretizing optimal control problems[J]. IEEE Transactions on Automatic Control, 1995, 40(10): 1793-1796.

[10] HUNTINGTON G T. Advancement and analysis of a Gauss pseudo-spectral transcription for optimal control problems[D]. Cambridge: Massachusetts Institute of Technology, 2007: 51-68.

[11] 高海濤, 張利民, 孫青林, 等. 基于偽譜法的翼傘系統歸航軌跡容錯設計[J]. 控制理論與應用, 2013, 30(6): 702-708. GAO H T, ZHANG L M, SUN Q L, et al. Fault-tolerance design of homing trajectory for parafoil system based on pseudo-spectral method[J]. Control Theory & Applications, 2013, 30(6): 702-708 (in Chinese).

[12] ZHANG L M, GAO H T, CHEN Z Q, et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudo-spectral method[J]. Nonlinear Dynamics, 2013, 72(1): 1-8.

[13] 焦亮, 孫青林, 亢曉峰. 基于混沌粒子群優化算法的翼傘系統軌跡規劃[J]. 復雜系統與復雜性科學, 2012, 9(1): 47-54. JIAO L, SUN Q L, KANG X F. Route planning for parafoil system based on chaotic particle swarm optimization[J]. Complex System and Complexity Science, 2012, 9(1): 47-54 (in Chinese).

[14] TAO J, SUN Q L, ZHU E L, et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]//34th Chinese Control Conference (CCC). Piscataway, NJ: IEEE Press, 2015: 2523-2528.

[15] 謝亞榮, 吳慶憲， 姜長生， 等. 粒子群算法在翼傘空投系統航跡規劃中的應用[J]. 航空兵器, 2010(5): 8-9. XIE Y R,WU Q X, JIANG C S, et al. Application of particle swarm optimization algorithm in route planning for parafoil airdrop system[J]. Aero Weaponry, 2010(5): 8-9 (in Chinese).

[16] 金敏, 魯華祥. 一種遺傳算法與粒子群優化的多子群分層混合算法[J]. 控制理論與應用, 2013, 30(10): 1231-1238. JIN M, LU H X. A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization[J]. Control Theory & Applications, 2013, 30(10): 1231-1238 (in Chinese).

[17] ADELFANG S I, SMITH O E. Gust models for launch vehicle ascent[C]//36th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1998: 1-8.

[18] 王曉光, 章衛國, 劉洋. 伴飛誘餌干擾下的自殺式無人機攻擊策略[J]. 航空學報, 2015, 36(9): 3137-3146. WANG X G, ZHANG W G, LIU Y. Suicide drones’ attack strategy on the condition of escort free-flight decoys influence[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 3137-3146 (in Chinese).

[19] 崔乃剛, 黃盤興, 路菲， 等. 基于混合優化的運載器大氣層內上升段軌跡快速規劃方法[J]. 航空學報, 2015, 36(6): 1915-1923. CUI N G, HUANG P X, LU F, et al. A hybrid optimization approach for rapid endo-atmospheric ascent trajectory planning of launch vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1915-1923 (in Chinese).

[20] 陳鶴, 方勇純, 孫寧, 等. 基于偽譜法的雙擺吊車時間最優消擺軌跡規劃策略[J]. 自動化學報, 2016, 42(1): 153-160. CHEN H, FANG Y C, SUN N, et al. Pseudo-spectral method based time optimal anti-swing trajectory planning for double pendulum crane systems[J]. Acta Automatica Sinica, 2016, 42(1): 153-160 (in Chinese).

[21] 孫青林. 翼傘自主歸航半實物仿真系統: CN201110174341.7[P]. 2012-01-18. SUN Q L. Hardware-in-the-loop simulation system for autonomous homing of the parafoil system: CN201110174341.7[P]. 2012-01-18 (in Chinese).

(責任編輯：張玉)

＊Corresponding author. E-mail: sunql@nankai.edu.cn

Trajectory planning of parafoil system with intricate constraints based on Gauss pseudo-spectral method

LUO Shuzhen1, SUN Qinglin1,*, TAN Panlong1, TAO Jin1, HE Yingping2, LUO Haowen3

1.CollegeofComputerandControlEngineering,NankaiUniversity,Tianjin300380,China2.AerospaceLife-SupportIndustriesLtd,AviationIndustryCorporationofChina,Xiangyang441003,China3.CollegeofAgriculturalEngineering,HenanUniversityofScienceandTechnology,Luoyang471003,China

The parafoil system is commonly affected by complex interferences, such as wind field and terrain environment, leading to imprecise homing and increasing control difficulty. A trajectory optimization of the parafoil system subjected to intricate constraints is proposed to realize accurate landing, flare landing against the wind, and global optimal control. A model for the parafoil system in the wind field is built. To transform the problem of trajectory optimization of the parafoil system in complex environment to the problem of optimal control with a set of nonlinear and intricate constraints, the complex terrain environment is converted into real-time path constraint by introducing into terminal constraints the terrain environment surface, the landing deviation and flare landing, and the objective function with minimum control consumption is defined. Gauss pseudo-spectral method is applied to transform the problem of optimal control with intricate constraints to the problem of easily solvable non-linear programming. Numerical simulation and experimental results show that the proposed method can efficiently plan out an optimal trajectory with high precision to meet the constraints in a variety of complex environments. A comparison with the existing method of chaotic particle swarm optimization demonstrates the outstanding performance of the proposed method.

parafoil system; intricate constraints; Gauss pseudo-spectral method; optimal control; trajectory planning

2016-04-23； Revised：2016-06-17； Accepted：2016-09-07； Published online：2016-09-26 09:50

URL：www.cnki.net/kcms/detail/11.1929.V.20160926.0950.002.html

s：National Natural Science Foundation of China (61273138, 61573197); National Key Technology Research and Development Program of China (2015BAK06B04); Key Technology Research and Development Program of Tianjin (14ZCZDSF00022); The Key Foundation of Tianjin (14JC2DJC39300)

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0254

2016-04-23； 退修日期：2016-06-17； 錄用日期：2016-09-07； 網絡出版時間：2016-09-26 09：50

www.cnki.net/kcms/detail/11.1929.V.20160926.0950.002.html

國家自然科學基金 (61273138， 61573197)； 國家科技支撐計劃 (2015BAK06B04)； 天津市科技支撐計劃 (14ZCZDSF00022)； 天津市重點基金 (14JC2DJC39300)

＊通訊作者.E-mail: sunql@nankai.edu.cn

羅淑貞， 孫青林， 檀盼龍， 等． 基于高斯偽譜法的翼傘系統復雜多約束軌跡規劃[J]． 航空學報, 2017, 38(3): 320363. LUO S Z, SUN Q L, TAN P L, et al. Trajectory planning of parafoil system with intricate constraints based on Gauss pseudo-spectral method[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 320363.

V448.231

A

1000-6893(2017)03-320363-11