基于Amorphous的無線傳感器網絡定位算法研究

北京信息科技大學自動化學院，北京 100101

一、引言

無線傳感器網絡（Wireless Sensor Networks）[1-3]作為一種全新的信息獲取和處理技術，是當前在國際上備受關注的、涉及多學科高度交叉的前沿熱點研究領域。

無線傳感器網絡的關鍵支撐技術之一是定位問題，定位問題也是無線傳感器網絡應用以及其他研究的基礎，如地理環境監測、軍事偵察、交通路況監測、搶險救災、醫療衛生中對病人的跟蹤等，所獲取的監測數據需要有相應的位置信息，否則，這些數據就是不確切的，甚至會失去采集數據的意義。

全球定位系統（GPS）可以為地球表面絕大部分地區（98%）提供準確的定位。但是受到成本、功耗、體積等因素的限制，在大規模的無線傳感器網絡中，為每個傳感器節點都安裝GPS設備是不太實際的方法。所以現有的一些定位方法中只是讓少數傳感器節點配備有GPS設備，然后通過一些數學的方式來估算未知傳感器節點的位置。

根據定位過程中是否測量實際節點間的距離，定位算法可分為：距離相關(Range-based)定位算法和距離無關(Range-free)定位算法。其距離相關的定位算法需要測量相鄰節點間的絕對距離或方位，并利用節點間的實際距離來計算位置節點的位置，定位精度高，但對節點本身硬件要求較高。距離無關的定位算法是根據網絡連通性等信息，利用節點間的估計距離計算節點位置，成本低、功耗小、抗噪能力強且硬件設備簡單。Amorphous定位算法就是一種距離無關的定位算法。

Amorphous定位算法是由麻省理工大學的Radhika Nagpal等人提出的[4]。此算法是通過計算未知節點與錨節點之間的跳數，估計平均每跳距離，用未知節點與錨節點之間的跳數乘以平均每跳距離來計算未知節點到錨節點的距離，再利用最小二乘法來計算位置節點的未知。Amorphous定位算法簡單，無需測距，實現容易。

現階段對Amorphous定位算法的改進方法主要有：跳數修正[5]；將已定位的未知節點轉化為錨節點來幫助其他節點進行定位[6]；而對Amorphous定位算法本身的參數優化研究較少。

本文詳細分析了Amorphous定位算法本身的參數，并通過仿真對參數進行優化。仿真結果表明，通過參數優化可以有效的提高Amorphous定位算法的定位精度。

二、Amorphous定位算法步驟

Amorphous[4-6]定位算法計算未知節點的位置的過程可以分為下面三個步驟：

1、計算未知節點到各個錨節點的跳數

網絡中的錨節點周期性的向鄰居節點發送攜帶位置信息的跳數數據包，并且在初始化時將跳數值設置為0，當錨節點的鄰居節點首次收到此廣播信息后，首先更新自身到錨節點的最小跳數和對應的錨節點的信息，然后再將更新后的信息轉發給其鄰居節點，直到檢測區域內所有待定位的節點都得到其到各錨節點的最小跳數。然后利用下式計算未知節點到各錨節點的跳數：

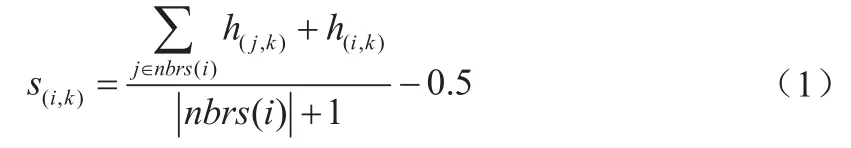
其中，s(i, k)—未知節點i到錨節點k的跳數；

h(j, k)—未知節點j到錨節點的k的最小跳數；

h(i, k)—未知節點i到錨節點k的最小跳數；

nbrs(i) —未知節點i的鄰居節點的集合；

|nbrs( i)|—未知節點i的鄰居節點的數目。

2、估算平均每跳距離

Amorphous算法是離線計算網絡每跳距離的，它需要在網絡部署之前就知道網絡的平均連通度，下式可以離線計算網絡平均連通度：

其中，nlocal—網絡的平均連通度；

n—節點總數；

S—檢測區域的面積；R—節點的通信半徑。

然后，用下式計算平均每跳距離：

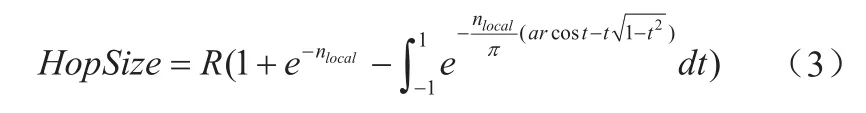
其中，HopSize—平均每跳距離；

nlocal—網絡的平均連通度；

R—節點的通信半徑。

Amorphous算法根據未知節點到各個錨節點的跳數和平均每跳距離來計算未知節點到各個錨節點的距離，計算公式如下：

其中，d(i,k)—未知節點i到錨節點k的距離；

HopSize—平均每跳距離；

s(i, k)—未知節點i到錨節點k的跳數；

3、計算未知節點的位置。

當未知節點獲得到至少3個錨節點的距離時，可以通過最小二乘法來計算未知節點的坐標。未知節點X=(x，y)T的坐標可以通過下面的公式計算得到：

其中，(xn , yn) —表示第n個錨節點的坐標；

dn—表示未知節點到第n個錨節點的距離。

分別用公式（5）前(n-1)個方程減去最后一個方程，得：

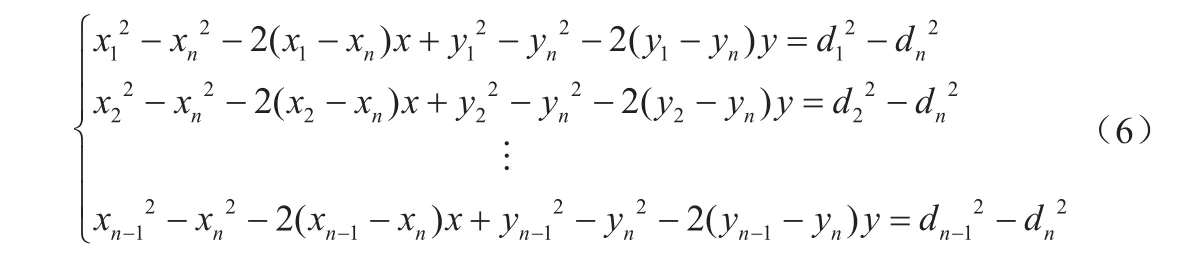
式（6）的線性方程可以表示成

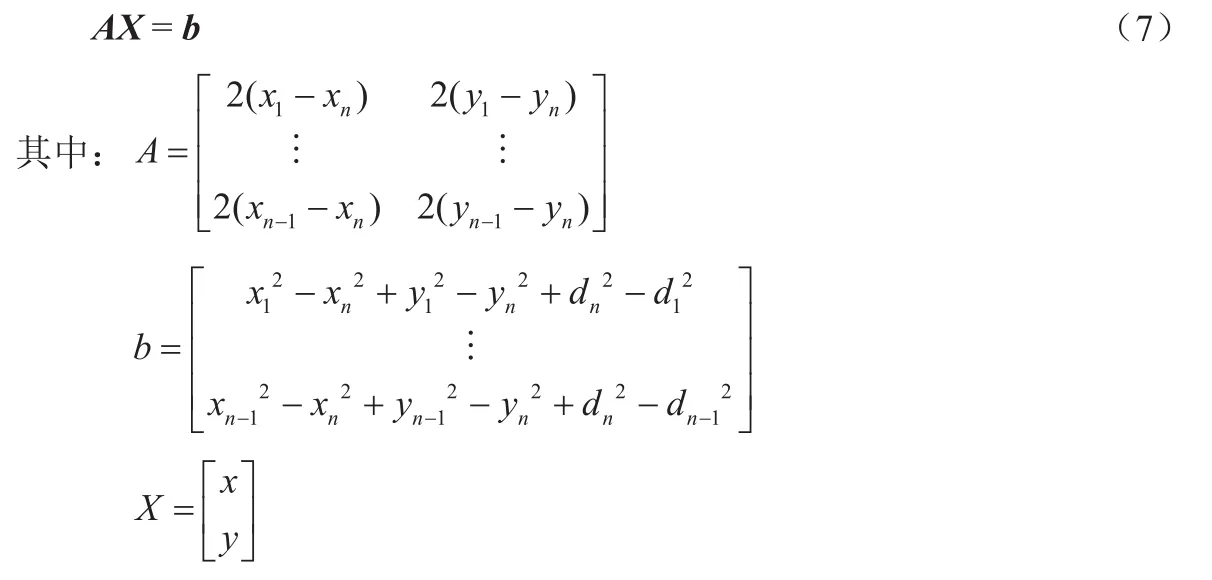
未知節點X 的坐標可以用標準的最小均方差估計方法得到，計算公式如下：

三、Amorphous算法的參數分析

1、錨節點的數目

Amorphous算法中，未知節點的位置是通過求解AX=b得到的。因為所有節點都是隨機分布的，當有些錨節點的位置重疊或者距離很近，或者有些錨節點分布在一條直線上時，使得包含錨節點位置信息的矩陣A在求逆矩陣的時候出現奇異矩陣或者NAN等情況，進而影響未知節點的定位精度。

2、節點的通信半徑

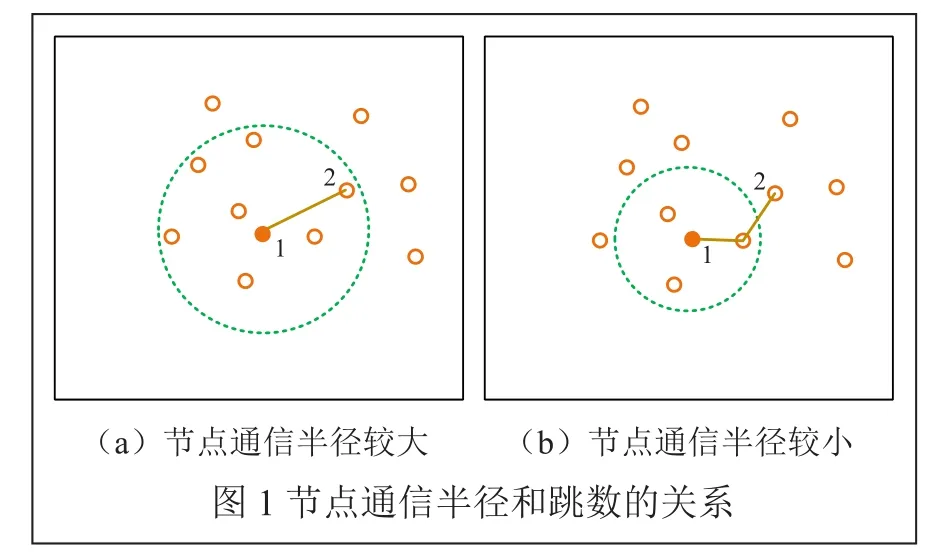
因為節點的跳數和節點的通信半徑是有關系的，節點的通信半徑發生變化時，節點之間的跳數也會發生變化。如圖1所示，虛線圓表示1號節點的通信半徑，圖1（a）的節點通信半徑大于圖1（b）的節點通信半徑，1號節點和2號節點的跳數在圖1（a）中是1跳，在圖1（b）中是兩跳。而Amorphous算法正是利用未知節點與錨節點的跳數來計算未知節點的位置，所以節點的通信半徑對定位精度有著很大的影響。

3、總節點的數目

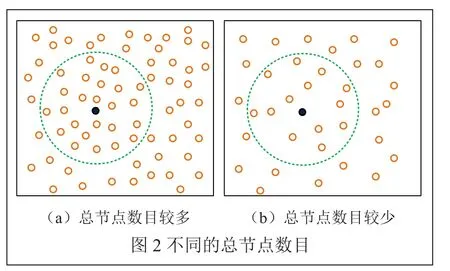
如圖2所示，虛線圓表示黑色未知節點的通信半徑，從圖2中可以看出，當圖2（a）和圖2（b）的節點通信半徑相同時，黑色未知節點的鄰居節點數目不同，那么根據式（1）計算得出的黑色未知節點到錨節點k的跳數就會不同。進而最終得到的未知節點的定位精度就會不同。

四、仿真結果與分析

在100m×100m的無線傳感器網絡監測范圍內，節點隨機的分布，利用MATLAB 仿真工具，給出了當錨節點個數、節點通信半徑和總節點數發生變化時，利用Amorphous算法得到的節點的定位誤差的變化，仿真中給出的每一個數值都是50次仿真結果求得的平均值，并且給出了仿真結果分析。

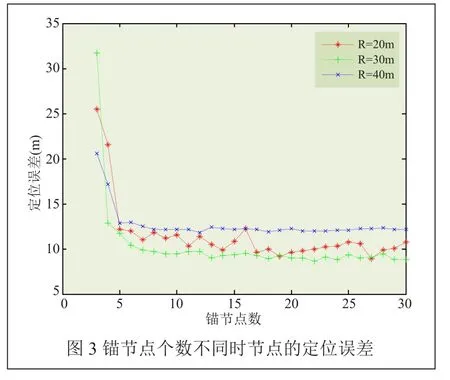
當總節點個數為100，錨節點個數從3～30變化時，分別對節點通信半徑R為20m、30m、40m時節點的定位誤差進行了仿真。仿真結果如圖3所示。

從圖3中可以看出，節點通信半徑不同時，當錨節點個數為10時，定位誤差能達到較小值；當錨節點個數從3～8變化時，節點定位誤差迅速減少；當錨節點個數繼續增加時，定位誤差趨于平緩。說明通信半徑不同，當錨節點達到一定數量時，其對節點定位誤差的影響將減小。

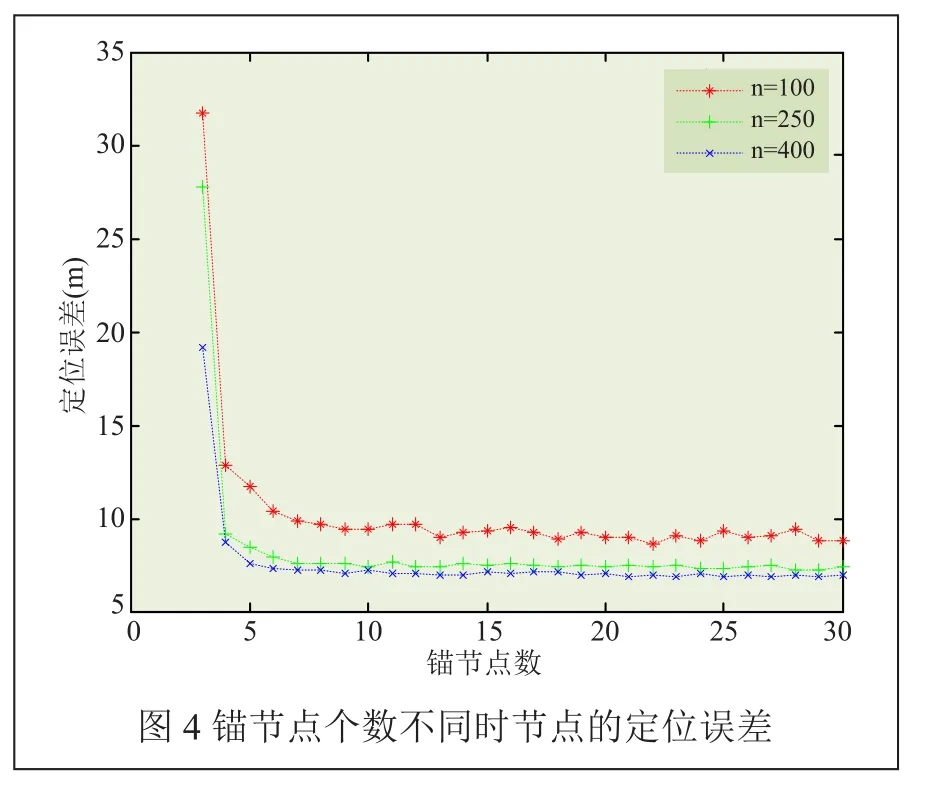
當節點通信半徑為30m，錨節點個數從3～30變化時，分別對總節點數n為100、250、400時節點的定位誤差進行了仿真。仿真結果如圖4所示。

從圖4中可以看出，總節點數目不同時，當錨節點個數為10時，定位誤差能達到較小值；當錨節點個數從3～8變化時，節點定位誤差迅速減少；當錨節點個數繼續增加時，定位誤差趨于平緩。說明總節點數目不同，當錨節點達到一定數量時，其對節點定位誤差的影響將減小。

從圖3和圖4可以看出，當節點通信半徑和總節點個數發生變化時，錨節點個數為10時，節點的定位誤差能降到較小值。因為錨節點自身的成本比一般節點要高，所以在100m×100m的監測區域中，利用Amorphous算法進行定位時，取10個錨節點即可。

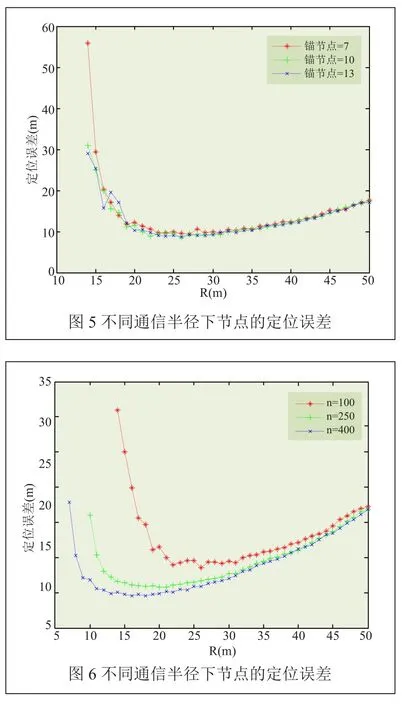
當總節點個數為100，通信半徑從14～50變化時，分別對錨節點個數為7、10、13時節點的定位誤差進行了仿真。仿真結果如圖5所示。

從圖5中可以看出，當通信半徑從14～20m變化時，節點定位誤差迅速減小，并且在通信半徑為23m時定位誤差達到了最小值，當通信半徑繼續增加時，節點的定位誤差呈上升的趨勢。說明在總節點個數為100，錨節點個數不同時，存在最優的通信半徑。

由圖3、4和5可以得出，在100m×100m的監測區域中，總節點個數為100時，隨機分布10個錨節點，節點通信半徑為23m時，定位誤差可以達到較小值。

當錨節點個數為10且通信半徑發生變化的情況下，對總節點個數為100、250、400時節點的定位誤差進行了仿真。仿真結果如圖6所示。

從圖6中可以看出，總節點個數不同時，節點的最優通信半徑也不同。當總節點個數為100時，在通信半徑為23m時，節點定位誤差可以達到較小值。當總節點個數為250時，在通信半徑為16m時，節點定位誤差可以達到較小值。當總節點個數為400時，在通信半徑為13m時，節點定位誤差可以達到較小值。

五、結論

本文對基于Amorphous的無線傳感器網絡定位算法進行了研究。 仿真結果表明，在100m×100m的無線傳感器網絡監測區域內，當錨節點個數連續變化時，在不同的總節點數目和通信半徑下，錨節點數目達到一定數量時，其對節點定位誤差的影響將減小；當通信半徑連續變化時，總節點數目為100時，在不同的錨節點個數下，存在最優通信半徑使定位誤差達到最小值；當通信半徑連續變化時，錨節點個數為10時，在不同的總節點個數下，存在不同的最優節點通信半徑使定位誤差達到最小值。所以利用最優節點通信半徑使定位誤差達到最小值。所以利用Amorphous算法進行定位時，由于傳感器節點本身能量的限制和錨節點成本較高的原因，可以選擇較優的參數來降低節點的定位誤差。