航姿參考系統中磁航向傳感器誤差標定與補償
北京信息科技大學,北京市傳感器重點實驗室,北京 100101
一、引言
航姿參考系統廣泛應用在無人機、UXO探測、石油鉆井等領域,其中的磁航向傳感器作為測量地球磁場的一部分為載體確定航向角。
為獲得高可靠性,高精度的導航信息,我們就要對磁航向傳感器進行有效地標定和補償。國內外學者從誤差模型和參數估計方面對磁航向傳感器誤差校正做了大量研究,目前感器標定方法主要有十六位置翻轉法,給定基準法,橢圓擬合法,遺傳算法等等[1]。在這些方法中,十六位置法雖然簡單易操作,但是精度卻不是很高;給定基準法在磁場強度變化不是很明顯時,具有不錯的補償精度,但是對外部儀器的要求較高;橢圓擬合法只需在水平面旋轉一周就可以自動擬合出橢圓函數[2],并且精度很高,但是橢圓擬合法,雖無需外部設備,卻只能應用在二維羅盤的平面補償;遺傳算法計算量大,控制復雜。
本文利用基于最小二乘法的改進的橢球擬合方法來對誤差進行標定補償,把標定前后的數據進行對比,結果表明該橢球標定法對磁航向傳感器的誤差有明顯的補償效果,并且無需借助外部設備,提高了系統的測量精度,降低了成本。
二、誤差分析及建模
記三軸磁矢量場μ=(μ1+μ2+μ3)T,傳感器輸出為υ=(υ1+υ2+υ3)T。在無干擾的理想條件下,磁航向傳感器沒有任何誤差,則傳感器輸出量與磁矢量場之間存在簡單的比例關系,即有:υ=kμ,其中k為標度因數(傳感器的靈敏度),在計入各種誤差后,υ、μ的關系將發生變化。
三軸磁矢量場的誤差主要有以下三種類型[3]:
1、靈敏度誤差
由于生產工藝等原因,造成三軸磁傳感器各軸的靈敏度不同,測量信號的放大電路特性也不完全相同引起的測量誤差統一為軸間靜態靈敏度誤差,由此得出數學模型為:
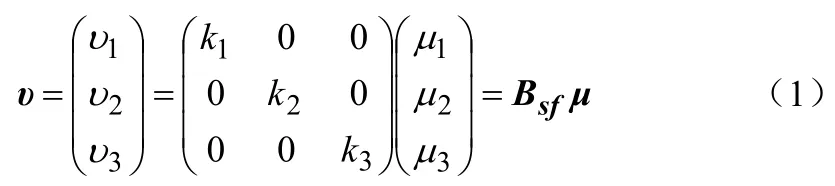
其中,k1,k2,k3—三軸磁航向傳感器的靈敏系數;
Bsf—靈敏度誤差陣。
2、非正交誤差
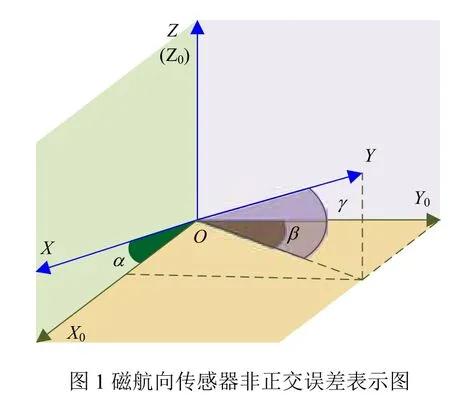
理想狀態的三軸磁傳感器各軸之間嚴格正交的,任一軸均不會感受到被測量場在另外兩軸上的分量。而在實際中由于在制造和安裝過程中三個磁傳感器的測量軸無法保證兩兩正交引起磁航向傳感器的非正交誤差。非正交誤差示意圖如圖1。
X0,Y0,Z0表示理想狀態下磁航向傳感器的矢量指向,X,Y,Z表示實際傳感器的三軸的指向;這里假設Z0和Z是重合的,且XOZ面和X0OZ0面重合,α是X軸在X0OZ0面與X0軸的夾角,β是Y在X0OY0面的投影和Y0的夾角;γ是Y和面X0OY0的夾角。誤差模型如式(2):
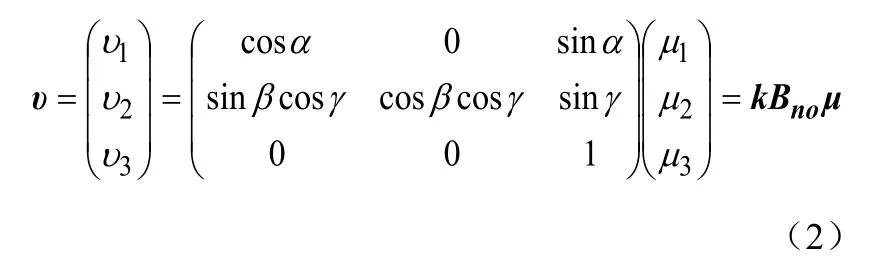
此模型是非正交誤差的一般描述,Bno非正交誤差陣。
3、零位誤差
使磁航向傳感器的輸出偏離原來的中心點的硬磁干擾讓傳感器產生了零位偏移,使其偏離球心。即產生了零位誤差。其誤差模型為(3)式:
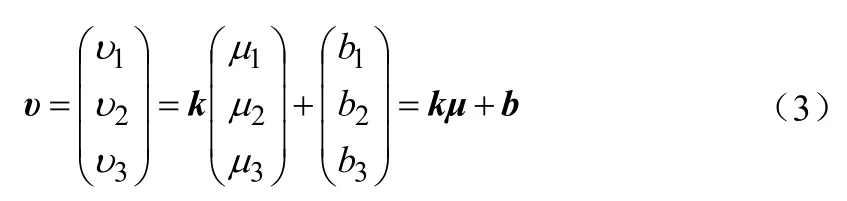
其中,b=(b1b2b3)T—零偏矢量。
綜合考慮以上三種誤差來源,得出一個統一的三軸磁航向傳感器的誤差模型如(4)式:

其中,υ—存在各種誤差下的實際輸出;
μ—理想狀況下次航向傳感器的輸出值;
K—誤差系數矩陣;

k1,k2,k3—磁航向傳感器的靈敏度;
α,β,γ—磁航向傳感器的軸間不正交誤差角。
式(4)顯然是一個線性誤差模型,對于除了以上三種誤差的其他誤差來源,屬于常數值得均可計入到矢量b中,而與矢量μ成比例關系的誤差均可用矩陣K來描述,譬如對于三軸磁強計受載體的磁場強度的干擾產生的羅差[4],其中軟磁干擾可被計入到K,硬磁干擾可計入到b中。因此式(4)可以統一描述磁航向傳感器的各種線性誤差,而不需要再去對具體的誤差來源進行區分。只要對式(4)的K、b進行確定,即可通過μ=K-1(υ-b)對其進行補償。所以,對磁航向傳感器的校正補償過程就是求K、b的過程。
對于三軸磁航向傳感器,式(4)所描述的誤差模型也稱作泊松模型,因為其最早是由法國的S.D.Poission 提出來的[5]。
三、誤差標定
本文在做誤差標定和補償時都是在以下假設中進行的:
(1)只考慮線性誤差,即誤差的高階項可以忽略;
(2)在討論涵蓋的空間、時間范圍內傳感被測磁場和傳感器的誤差均為定常的;
(3)噪聲項均為零均值高斯噪聲。
三軸磁航向傳感器的誤差校正,本質上就是確定誤差模型即式(4)中的K和b,從而由磁航向傳感器的輸出量υ來算出被測量μ的準確值,即為μ=K-1(υ-b)。記J=K-1,則μ=J(υ-b),因此,也就等價于求J和b,采用這種形式更方便進行誤差補償。
校正過程中,μ為未知量,利用μ的某種約束實現校正。這里使用的約束是矢量場μ的強度不變,記理論的三維矢量和為μb,則方程(4)可轉化為:
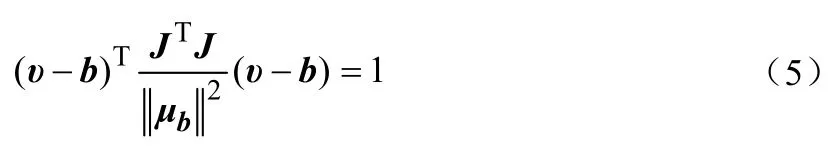
其中,J—誤差系數矩陣的逆;
υ—磁航向傳感器的理論輸出;
b—磁航向傳感器的零偏量。
由最優擬合橢球曲面的二次函數一般式:F(ξ,z)=ax2+by2+cz2+2dxy+2exz+2fyz+2px+2qy+2rz+l=0,用矩陣記號來表示為:

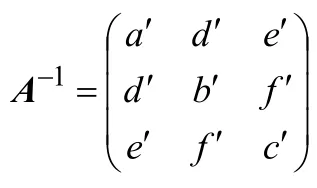
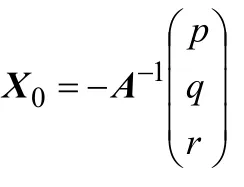
根據式(5)和式(6)得出:
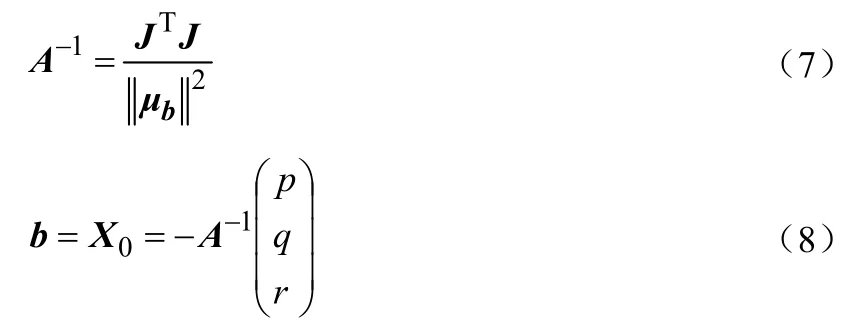
經過計算得出:
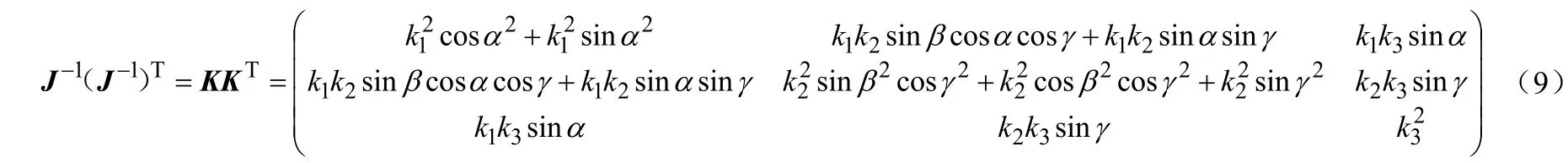
在實際應用中一般α、β、γ這三個正交角都是非常小的,所以式(9)可以化簡為式(10)所示:
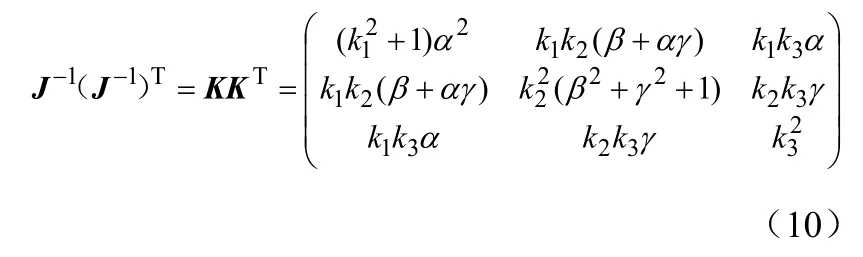
根據橢球擬合的參數A和X0,算出傳感器誤差參數估計值為:
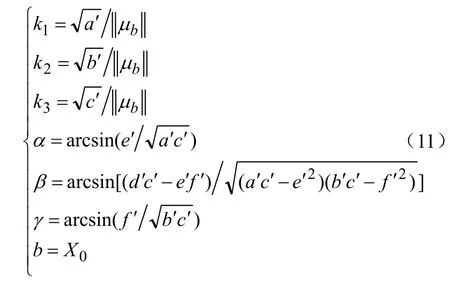
得出的誤差參數估計值為后續磁航向傳感器的誤差修正模型的求解做鋪墊。
四、誤差補償
由前文可得磁航向傳感器的誤差修正模型為

其中,J通過計算得:
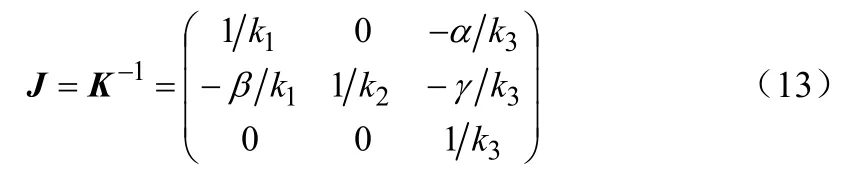
將(13)式代入(12)式可得
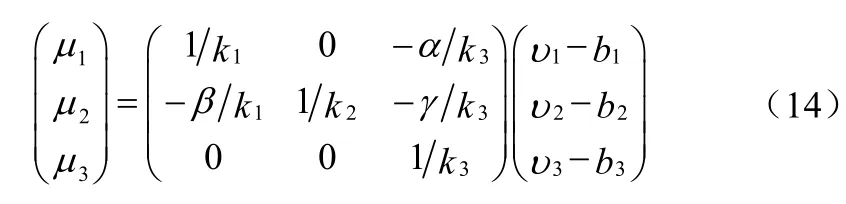
將(11)式中各參數代入(14)式可以獲得磁航向傳感器的誤差修正模型,然后就可以對測量結果進行誤差補償了。
五、實驗結果及分析
為了驗證該補償方法是否正確有效,本文利用的是MPU9250的內部磁航向傳感器進行的誤差補償。
MPU9250是美國InvenSense 出產的MPU9250型號的傳感器。MPU9250是一個復合芯片,具有3個加速度A/D輸出和3個陀螺儀角速度A/D輸出,其位數均為16位,同時還有三個6位磁力計A/D輸出,其可靠性高,測量范圍大,成本小,耗能少,因此我們選用該型號傳感器進行實驗數據的采集和分析驗證。
實時輸出磁航向傳感器的數據,然后根據本文提出的橢球擬合法進行誤差的標定補償。并利用MATLAB 軟件進行了實驗數據的處理。首先選擇干擾較小的磁場環境,以任意角度變換MPU9250的姿態,實時采集三軸磁傳感器的數據,將采集的數據通過MATLAB記錄,繪制出數據軌跡三維圖如圖2。
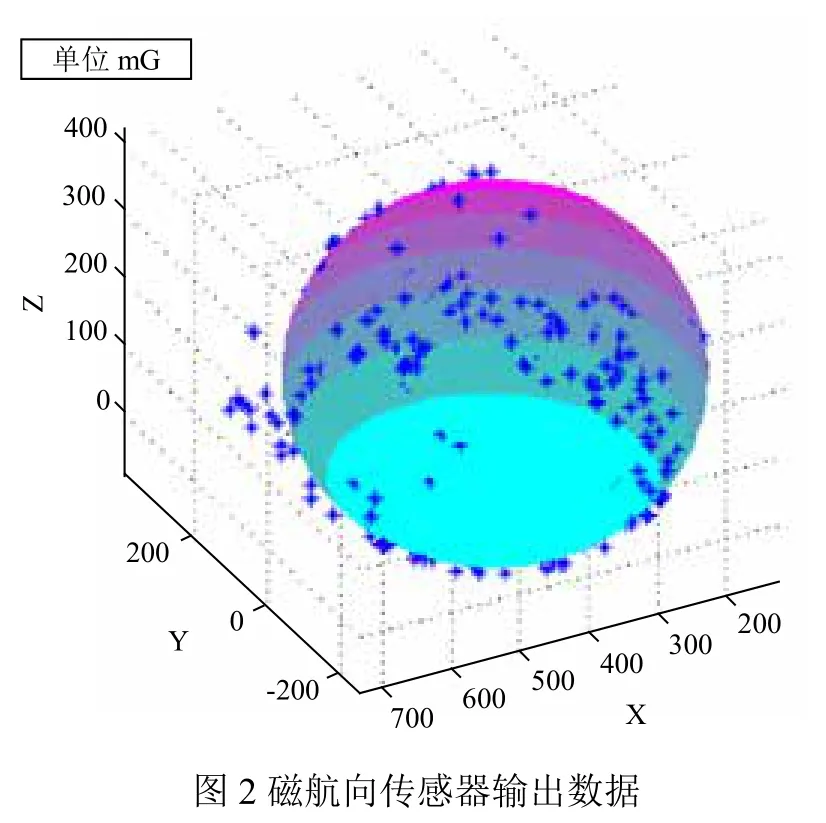
從圖2我們可以觀察到磁傳感器的軌跡基本上都在橢球面上,只有幾個點在橢球外。因此避免突變磁場發生,把其放在無干擾磁場或少干擾磁場中進行采集數據,同時注意把三軸磁傳感器輸出的數據均勻的分布在橢球上,從而提高誤差補償的精度。圖2磁場強度單位是mG,而1T=107mG。由橢球擬合的磁傳感器的誤差標定方法,根據公式(11)計算得出磁航向傳感器各個誤差補償系數:
k1=0.2816×105V/T,k2=0.2808×105V/T,k3=0.2793×105V/T,α=1.7546°,β=-0.8296°,γ=-0.1577°,b1=-0.1506×10-5T,b2=-0.4326×10-5T,b3=0.5740×10-5T。
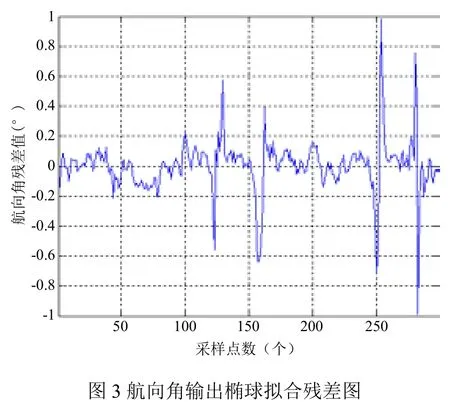
至此完成了誤差標定,將標定好的系數代入式(14)即可得到了誤差補償后的磁航向傳感器的輸出數據。然后我們進行轉臺實驗,將磁航向傳感器解算出的航向角與實際的航向角進行比較,進而確定誤差補償的精度。如圖3即為航向角輸出橢球擬合殘差圖。
實驗結果表明本文提出的改進后的橢球擬合法在標定磁航向傳感器的誤差補償系數上取得了顯著成效,能夠準確的將已經平移變形的橢球面逆變回圓球面,而且誤差控制在了1°之內,實現了磁航向傳感器的安裝等誤差的高精度補償。
六、結束語
本文根據磁航向傳感器的誤差特性,分別建立了靈敏度誤差,非正交誤差,零位誤差三種誤差模型,并利用改進后的橢球擬合法對磁傳感器采集的數據進行標定補償,然后通過實驗驗證了此方法的有效性和準確性。該算法簡單易行,省時,并且實現了高精度補償,能夠在三軸矢量傳感器的誤差標定補償中得到廣泛應用。

