核電站循環水系統進水池結構優化分析

聶小棋, 葉學民, 李達然, 曹祐群, 張瑩瑩

(1. 華北電力大學 能源動力與機械工程學院， 河北保定 071003;2. 國核電力規劃設計研究院， 北京 100095)

核電站循環水系統進水池結構優化分析

聶小棋1,2, 葉學民1, 李達然2, 曹祐群2, 張瑩瑩1

(1. 華北電力大學 能源動力與機械工程學院， 河北保定 071003;2. 國核電力規劃設計研究院， 北京 100095)

通過控制變量的方法，對某核電站進水池擬定的結構參數大小進行適當調整，并通過數值模擬方法得出并推薦了進水池主要結構參數選取范圍，從數值模擬的角度證實了該進水池擬定結構參數大小的合理性。

核電站； 進水池; 結構參數; 數值模擬

核電站循環水系統的進水池是泵房前池與循環水泵進口之間的銜接部分，其作用是平穩地過渡前池水流使之均勻擴散，為水泵提供良好的進水流態。循環水泵能否高效運行很大程度上取決于進入其中的水流流態。

當泵房前池的結構尺寸設計不合理時，池內水流容易發生紊亂，進而影響水泵正常運行，嚴重時還會造成水泵振動甚至停機[1]。范淑琴等[2]通過模型試驗發現，不良的進水流態能降低水泵效率4%～16%；邱靜等[3]針對水泵機組不規律的振動現象，通過試驗對前池水流進行了深入的觀察研究，指出池中渦旋是引起機組不規則振動的主要原因；丁天壽[4]通過試驗研究，認為前池流態紊亂是水泵效率降低的主要因素；Deeny等[5-6]指出進水池內的漩渦是影響水泵安全運行的主要因素；Akalank等[7]通過實驗發現，當池內吸氣漩渦含氣量達到1%時，會嚴重影響水泵的運行效率；日本工程協會[8]、美國陸軍工程兵團[9]等依據大量的試驗給出了進水池重要結構參數的參考范圍，但這些設計參數范圍有較大的出入，原因可能在實驗條件、實驗標準及應用的場合有差異。

核電站的循環水量比一般火電機組要大，因此進水池中水流流態相比火電站進水池也會更加復雜。國內對核電站進水池方面的研究比較少，吉紅香等[10]通過物理模型實驗發現，進水池工況好壞直接影響到水泵的運行效率，指出規劃良好進水池結構的必要性；王保田[11]在某核電站一期工程循環水泵進水流道模型試驗中發現，通過在水泵吸水口處加裝底面椎體能有效阻止水中渦，確保水泵的安全高效運行。

國內外文獻對核電站進水池數值模擬方面的研究較少，許多文獻通過數值軟件對進水池在其他場合的應用進行了模擬并得出相關結論，但這些結論往往由于應用場合以及試驗條件的差異，不能完全應用于核電站進水池。因此，筆者采用數值模擬方法對某核電站的進水池進行全三維定常流場計算，探討該進水池的結構參數及進水流量的不同對池中水流流態造成的影響，著重觀察進水流道入口處的流態是否均勻，同時得出最佳的進水池結構參數的參考范圍，為實際試驗提供依據和參考。

1 核電站循環水系統進水池主要參數

進入水泵的水流一部分從喇叭管前部進入水泵，還有一部分從喇叭管的兩側及后側進入水泵。理想的進水流場是各個方向進入水泵的水流流量應盡可能相等，因此進水池結構參數的確定要以此為原則。

該核電站進水池為開敞式矩形結構形式，見圖1。

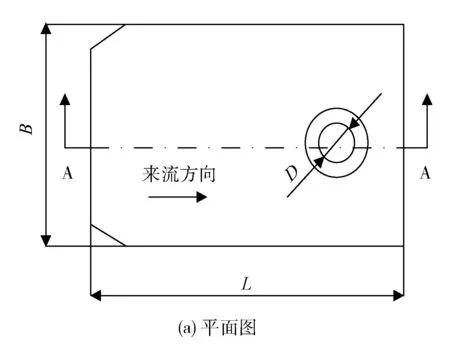
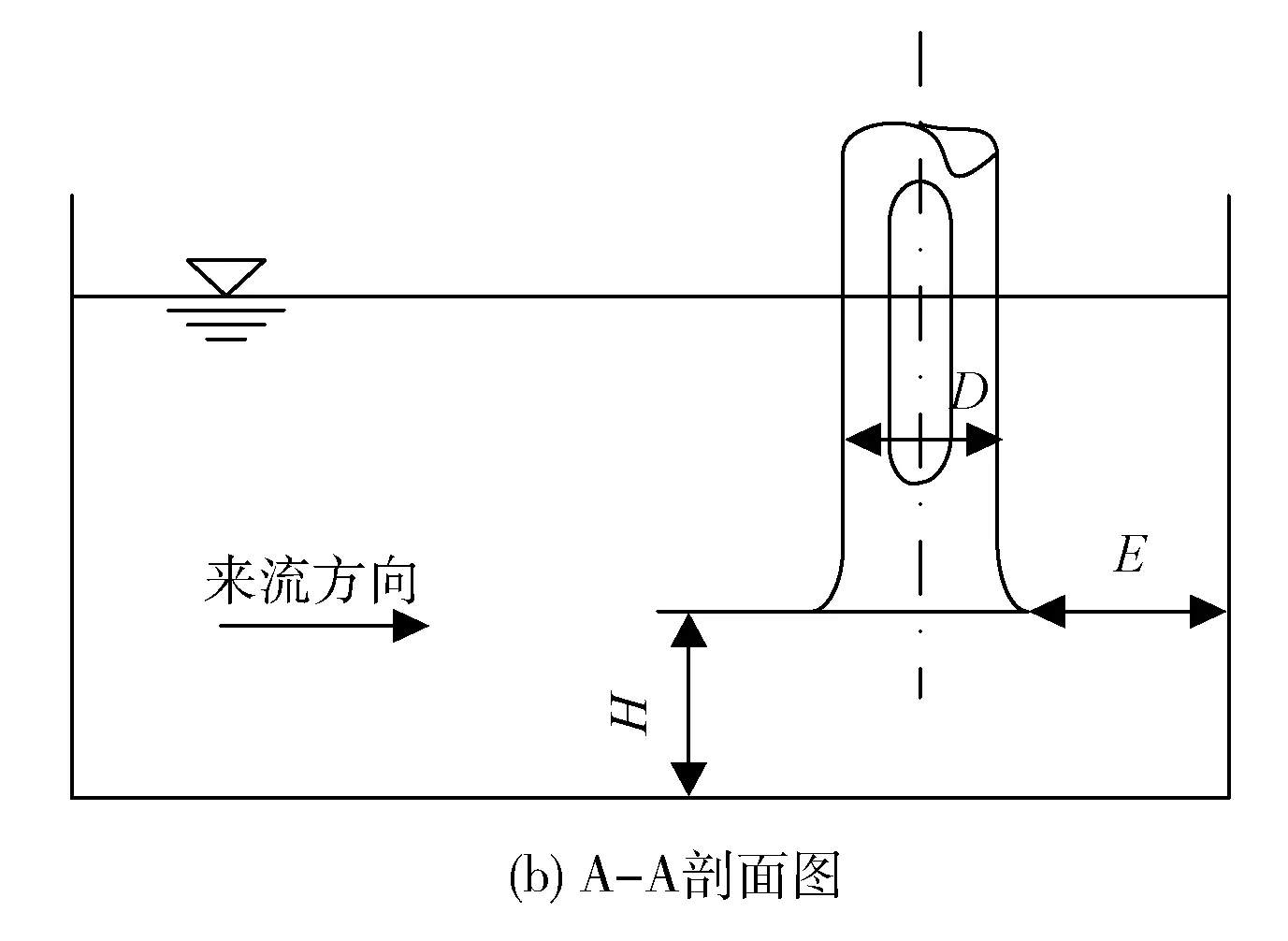
圖1 進水池示意圖

進水池主要參數為：池長L=5.75D、池寬B=3.62D、懸空高H=0.65D、后壁距E=0.68D及淹沒深度h(吸水管直徑D=2.8 m，進水池的各個幾何參數大小以D作為基準參照表示)。進水池的水泵采用金屬混流泵，循環水量Q=20.42 m3/s，水池水深8.7 m。進水池入口處有一小段擴散部分，擴散段長度1.8 m，擴散角29°。進水池入口高3.3 m，寬8 m。數值模擬將以該核電站進水池結構參數為參照，通過控制變量的方法改變進水池幾個主要參數，然后進行多次模擬，以期得出最佳水池結構參數的參考范圍，同時驗證該核電站進水池結構參數的合理性。

2 進水池的數值建模

計算采用標準k-ε模型，壁面函數采用非平衡壁面函數，并應用Simplec算法，離散精度取為二階迎風格式。模型進口給定為速度進口邊界，速度方向垂直于進口界面。由于吸水管長相比管徑足夠大，可以認定吸水管出口斷面處流動是充分發展的，故出口采用自由出流邊界條件。進水池表面為自由表面，忽略液面與空氣之間的切應力以及熱交換，對液面采用剛蓋假定，即自由表面設置為對稱邊界條件。不同區域的交界面上定義interface使絕對流動速度連續，因而實現各個區域交界面上流體能自由貫穿。

網格劃分采用分塊網格技術，根據該進水池不同部位的結構特點。對邊界結構復雜的區域采用適應性強的非結構化網格單獨劃分網格，部分區域，如吸水管采用cooper方式劃分六面體結構網格。吸水管壁面處受到流體的黏性作用，速度梯度較大，為捕捉壁面處的流動特征，在吸水管壁面設置邊界層網格。

網格無關性驗證時，每個模型網格劃分的全局最大尺寸為0.15 m，吸水管邊界層第一層網格高度為1 mm，邊界層網格層數為20層，每層網格增長因子為1.2。以池長L=5.75D、池寬B=3.5D、懸空高H=0.5D、后壁距E=1D為例，此時模型網格數為291萬。另取模型網格全局最大尺寸為0.1 m，邊界層網格參數不變，網格數340萬，此時精度和前者相差不多，但是計算時間會增加。由于291萬的網格可以同時滿足計算時間和計算精度的要求，故模型網格全局最大尺寸選取為0.15 m是合適的。基于此在進行模擬時，對進水池結構參數進行變動后，每個模型全局最大尺寸都取為0.15 m，邊界層網格參數不變選取如上，能滿足網格無關性要求。

3 水力性能優化目標函數

為了定量對進水池參數進行優化設計，建立如下目標函數：

(1) 速度均勻度Vu最大的目標函數。

進水池流態對水泵葉輪的影響主要體現在水泵葉輪前，進水斷面處的流速分布，進水流速分布是否均勻會影響到水泵的運行性能。均勻度越高，葉輪前進口斷面處的均勻性就越好，水泵運行性能自然也會更佳。

(1)

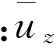
(2) 水力損失hw最小的目標函數。

在考慮進水池最佳結構參數時，水力損失是很重要的參考指標，根據伯努利方程引入水力損失量hw的概念，建立進水池入口斷面和吸水管進口斷面處的水力損失量目標函數。

hw=E2-E1=

(2)

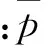
4 數值結果及分析

4.1池寬影響

采用4種不同池寬的方案進行了數值模擬，每個方案中進水池主要參數見表1。

表1 池寬數值模擬方案

圖2為池寬對斷面均勻度的影響，圖3為池寬與水力損失量的關系。

圖2 池寬對斷面均勻度的影響

圖3 池寬與水力損失量的關系

從圖2可以看出：當池寬為1.5D時，泵入口斷面處均勻度最差；當池寬為4.5D時，斷面處均勻度最佳。隨著池寬的增加，泵入口斷面均勻度不斷增加，池寬從1.5D增加到4.5D，斷面均勻度提高了37.52%；但隨著池寬的不斷增加，斷面均勻度增加的幅度不斷減小，池寬從1.5D增加到2.5D，均勻度增加了23.5%，而池寬從2.5D增加到3.5D時，均勻度增加了8.06%。主要原因是當池寬較小時，池中流速變大，進入水泵的流速分布不均勻，同時過窄的池寬也會使得流向喇叭口的流線曲率增加，容易在喇叭口附近形成漩渦，使得吸水管進口斷面流速分布不均勻。當水池寬度變大時，流速降低，同時水池有更大的空間讓水流流向水泵時均勻平穩過渡，因此水泵進口斷面流速分布更加均勻。不過增大水池寬度的同時，會增加開挖工程量，提高工程成本。當池寬過大時，水池壁面的導向作用也會變差，在池中容易形成偏流和回流，反而可能會惡化進水條件。從圖3可以看出：隨著池寬的不斷增加，水力損失是不斷減小的。基于以上分析，推薦進水池池寬選取3D～4.5D。該核電站池寬擬選定為3.62D，在推薦范圍內。

4.2池長影響

采用4種不同池長的方案進行了數值模擬，每個方案中進水池主要參數見表2。

表2 池長數值模擬方案

圖4為池長對斷面均勻度的影響，圖5為池長與水力損失量的關系。

圖4 池長對斷面均勻度的影響

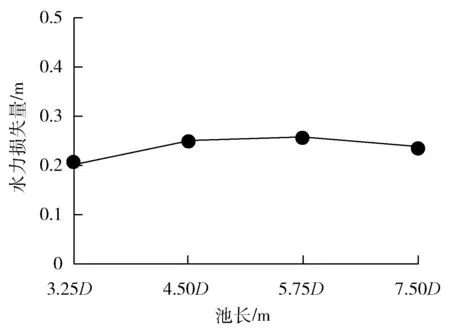
圖5 池長與水力損失量的關系

從圖4、圖5可以看出：當池長大于一定的程度，隨著池長的增加，水泵進水口斷面均勻度以及水力損失量變化均不明顯。因為池長增加到一定的長度后，從進水池進口流入的水流有足夠的空間和時間均勻擴散，平穩過渡到水泵進水口處，其斷面處均勻度較佳，不再明顯變化，水力損失量變化同理。此外增加水池長度，會增加開挖工程量，提高工程成本。基于以上分析，推薦池長為3.5D～6D。該核電站進水池池長擬選定為5.75D，在推薦范圍內。

4.3后壁形狀影響

采用4種不同后壁形狀的方案進行了數值模擬，每個方案中進水池主要參數見表3。

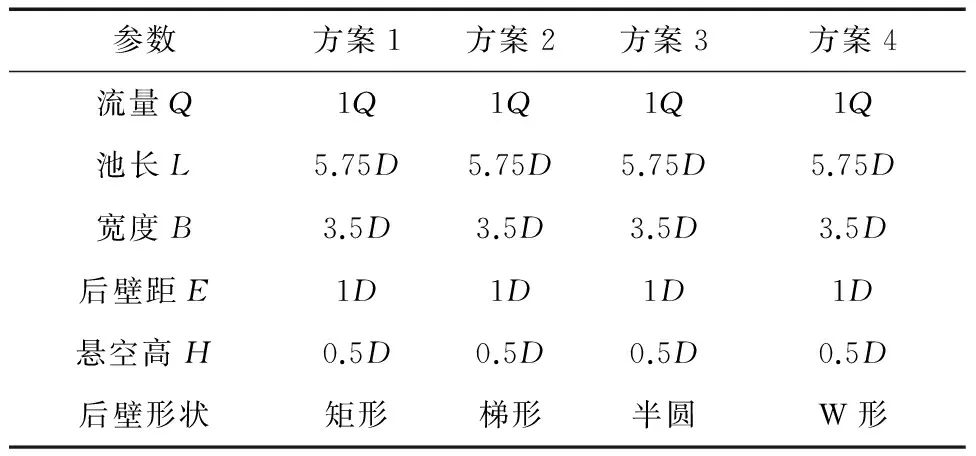
表3 后壁形狀數值模擬方案

圖6為筆者模擬采用的進水池4種不同形狀的后壁。

圖6 不同形狀后壁

表4為后壁形狀與均勻度、水力損失量的關系。

表4 后壁形狀與均勻度和水力損失量的關系

從表4可以看出：后壁形狀從矩形、梯形、半圓到W形，吸水管進口端面的均勻度是不斷增加的，進水池采用W形后壁時均勻度相比于矩形后壁提高了1.33%。因為矩形后壁進水池在后壁直角區域為低速區，在該處容易形成回流，使水流流速分布不均勻，不利于水泵進水口處的流態。梯形后壁形狀在矩形后壁的基礎上進行了結構改良，后壁處的回流區基本消失，對于改善流態起到了較好的效果。半圓后壁形狀的進水池同樣避免了池中回流的產生，同時池中流體流線和后壁形狀也比較一致，因而該后壁有良好的整流效果，進水口斷面處均勻度較高。對于W形后壁進水池，后壁中間突出的壁面部分比較接近水泵進水口，能有效改善進入水泵的水流流態，抑制其漩渦和回流的產生，此外該形狀后壁和水流流線比較吻合，因此在所羅列的四種后壁形狀中，W形后壁具有最佳的整流效果，能使得進水口斷面處的均勻度最佳。

從表4可以看出：矩形后壁進水池水力損失量最大，W形后壁進水池水力損失最小，梯形和半圓后壁進水池水力損失量居中。W形后壁相比于矩形后壁水力損失量減少了13.9%。值得指出的是，半圓后壁進水池水力損失量和矩形后壁進水池水力損失量差不多，高于另外兩種后壁進水池，原因在于半圓后壁進水池由于結構特點容易在后壁附近形成漩渦，其增加了水力損失量。W形后壁進水池由于其較好的結構特點及整流作用，使得水力損失量最小。

該核電站進水池擬采用的是矩形后壁，基于以上分析，進水池后壁形狀建議采用W形后壁。

4.4后壁距影響

采用4種不同后壁距的方案進行了數值模擬，每個方案中進水池主要參數見表5。

表5 后壁距數值模擬方案

圖7為后壁距對斷面均勻度的影響，圖8為后壁距與水力損失量的關系。

圖7 后壁距對斷面均勻度的影響

圖8 后壁距與水力損失量的關系

從圖7、圖8可以看出：隨著水泵后壁距離增加，均勻度越高，即水泵進水口斷面流速分布更加均勻，水力損失量呈逐漸下降趨勢。后壁距為1D相比較于后壁距為0.1D時，均勻度提高了2.89%，水力損失量降低了29.02%。原因在于當后壁距離很小時，水流從前面和兩側進入水泵的流量要更多，后側水流進入得較少，此外水流沖擊后壁折返過程中，擴散還未充分均勻就進入了水泵，因此從水泵四周進入吸水管的水流是不均勻的，同樣水力損失量也是最大的。當后壁距增加時，水流從四周流入水泵更加趨于均勻，且沖擊后壁折返的水流有更大空間平穩過渡到水泵進水口處，因而流速分布更加均勻，水力損失量也越來越小，趨于定值。需要指出的是，當后壁距過大，水流容易產生吸氣渦而影響水泵的正常運行。

基于以上分析，推薦進水池后壁距為0.3D～1D。該核電站進水池后壁距擬定為0.68D，在推薦范圍內。

4.5懸空高影響

采用4種不同懸空高的方案進行了數值模擬，每個方案中進水池主要參數見表6。

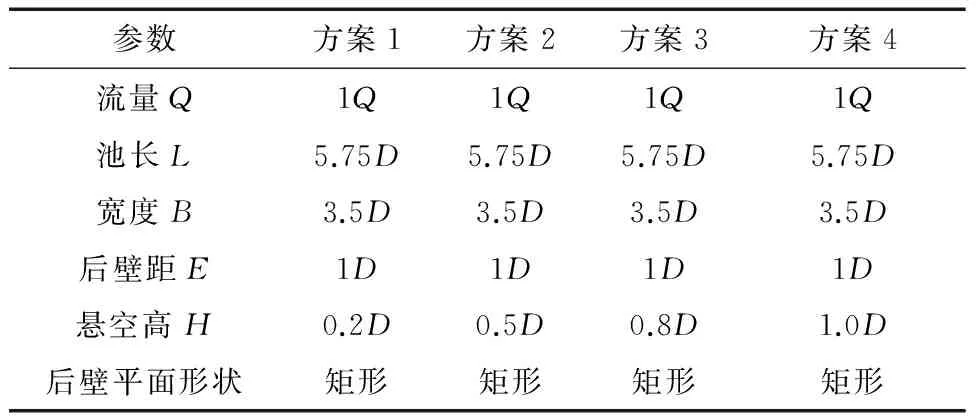
表6懸空高數值模擬方案

圖9為懸空高對斷面均勻度的影響，圖10為懸空高與水力損失量的關系。

圖9 懸空高對斷面均勻度的影響

圖10 懸空高與水力損失量的關系

懸空高能較大程度上影響進水池中流態，從圖9、圖10可以看出：隨著懸空高的增加，進水口斷面水流均勻度變化過程為先增加后減小，流體水力損失量則不斷減小，但是減小的幅度在隨之降低。懸空高為0.5D時，均勻度最大比懸空高為0.2D時增加13.59%，水力損失減少23.92%。懸空高為1.1D時，水力損失相比于0.8D減小15.69%。懸空高較低時，流向喇叭口的流線曲率增加，速度梯度變化大，容易在喇叭口附近形成漩渦，使得吸水管進口斷面流速分布不均勻,水力損失也很大。懸空高過大時，一方面增加了土建工程量，另外容易在液面形成吸氣旋渦，使流態變差同時還能影響到水泵的正常運行。

基于以上分析，推薦進水池懸空高為0.5D～1D。該核電站進水池懸空高擬定為0.65D，在推薦范圍內。

4.6流量影響

采用4種不同流量的方案進行了數值模擬，每個方案中進水池主要參數見表7。

表7 流量數值模擬方案

為了加強對進水池相關參數，引起水流流態變化的認識，現引入流量作為考察的變量。當流量變化時，水泵進水口斷面均勻度以及流體水力損失量結果見圖11、圖12。

圖11 流量對斷面均勻度的影響

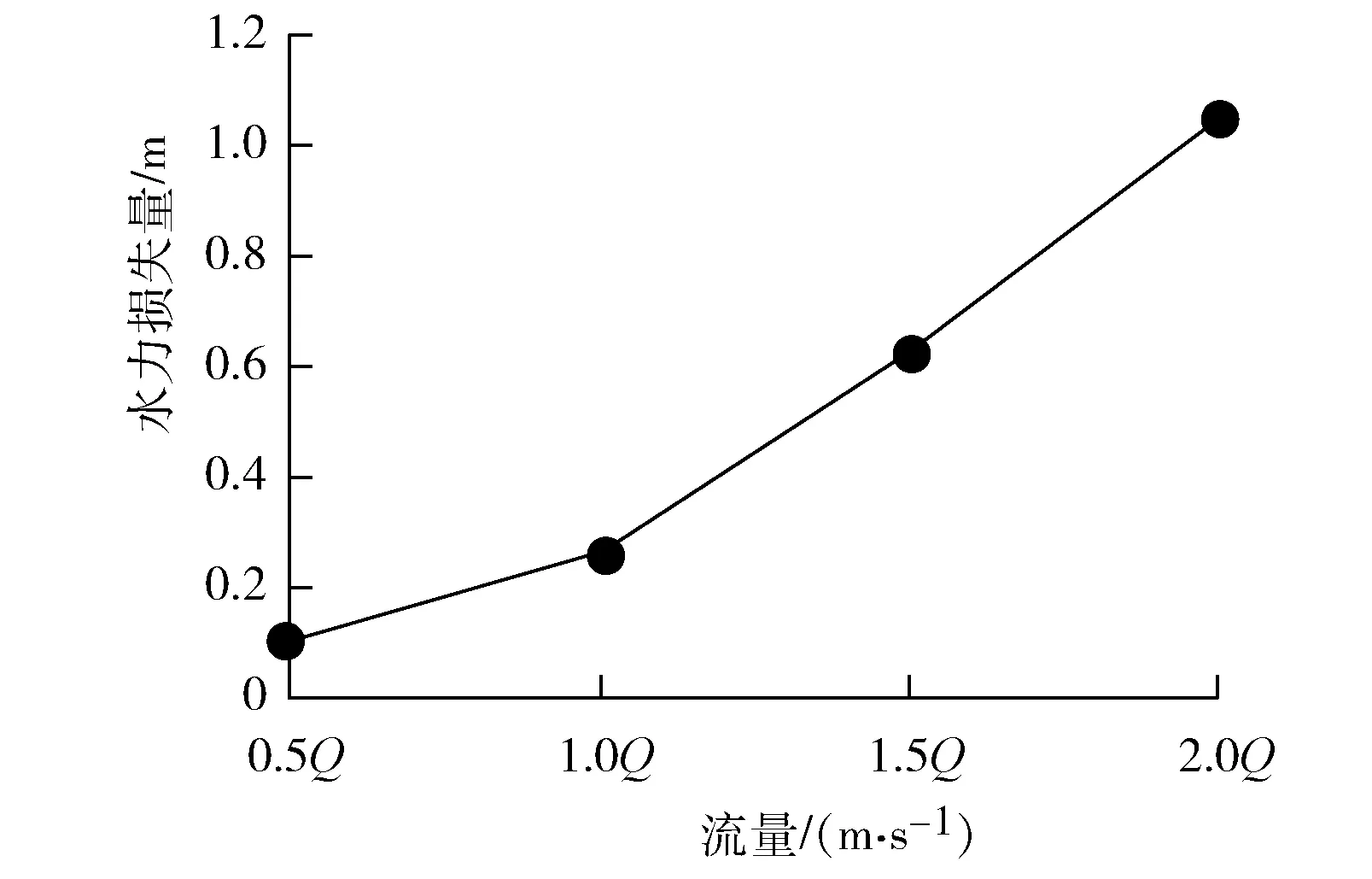
圖12 流量與水力損失量的關系

從圖11、圖12中可以看出：隨著流量不斷增加，均勻度逐漸減小，水力損失不斷增加，且水力損失量和流量近似于二次函數的關系。當進入水池的流量不斷增加，水流流速也會隨之變大，使得池中的流態趨于復雜，池中更容易出現偏流、回流的不良流態，因此均勻度會下降，而水力損失量會增加。

5 結語

(1) 通過控制變量的方法，對某核電站進水池擬定的結構參數進行適當調整，并通過數值模擬方法得出并推薦了進水池主要結構參數合理的選取范圍：池寬3D～4.5D，池長3.5D～6D，后壁距0.3D～1D，懸空高0.5D～1D。

(2) 將某核電站進水池擬定的結構參數和筆者推薦參數范圍進行對照，得出如下建議：將進水池后壁形狀改為W形，其他參數大小不變。筆者從數值模擬的角度，證實了該進水池結構參數選取的合理性，并提出了改進措施。

(3) 數值模擬結果滿足網格無關性要求，所得到的結果可供同類場合參考。

[1] 中華人民共和國水利部. 泵站設計規范[M]. 北京: 中國計劃出版社, 1997.

[2] 范淑琴, 仲付維. 抽水站整體模型試驗研究[J]. 水利學報, 1987, 18(11): 45-50.

[3] 邱靜, 黃東, 黃本勝, 等. 某大型泵站機組振動原因分析及防振臨時工程措施[J]. 中國農村水利水電, 2004(12): 103-105.

[4] 丁天壽. 1200LW-60大型泵低效原因淺析及改善措施探討[J]. 西北水力發電, 2006, 22(5): 89-91.

[5] DENNY D F. An experimental study of air-entraining vortices in pump sumps[J]. Proceedings of the Institution of Mechanical Engineers, 1956, 170(1): 106-125.

[6] REDDY Y R, PICKFORD J A. Vortices at intakes in conventional sumps[J]. Water Power, 1972, 24(3): 108-109.

[7] JAIN A K, RAJU K G R, GARDE R J, et al. Vortex formation at vertical pipe intakes[J]. Journal of the Hydraulics Division, 1978, 104(10): 1429-1445.

[8] Pumping Station Engineering Working Group of Japan Association. Pumping station engineering handbook[M]. Tokyo: Japan Association of Agricultural Engineering Enterprises, 1991.

[9] U. S. Army Corps of Engineers. Hydraulic design guidance for rectangular sumps of small pumping stations with vertical pumps and ponded approaches[R]. Washington D C: U. S. Army Corps of Engineers ,1998.

[10] 吉紅香, 邱靜, 林美蘭, 等. 某核電廠一期工程循環水泵房進水流道物理模型試驗研究[J]. 廣東水利水電, 2010(10): 20-23.

[11] 王保田. 某核電站一期工程循環水泵進水流道模型試驗探討[J]. 中國電力, 2014, 47(5): 113-117, 135.

StructureOptimizationofaPumpSumpinCirculatingWaterSystemofNuclearPowerPlant

Nie Xiaoqi1,2, Ye Xuemin1, Li Daran2, Cao Youqun2, Zhang Yingying1

(1. School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China; 2. State Nuclear Electric Power Planning Design & Research Institute, Beijing 100095, China)

By control variable method, an adjustment of simulated structural parameters was carried out for the pump sump of a nuclear power plant, after which some parameter ranges were recommended for the sump. Above structural parameters of the pump sump were proved to be rational by numerical simulation.

nuclear power plant; pump sump; structural parameter; numerical simulation

2017-03-03；

2017-03-18

聶小棋(1992—)，男，在讀碩士研究生，主要從事流體結構優化和流體換熱研究。E-mail: 156583707@qq.com

TM623.4; TV 136. 2

A

1671-086X(2017)06-0420-06