第一寄存器小Qubit量子計算攻擊RSA研究

王寶楠，陳宇航，尹寶，胡風，張煥國，王潮

(1. 上海大學(xué)通信與信息工程學(xué)院特種光纖與光接入網(wǎng)省部共建教育部重點實驗室，上海 200072；2. 武漢大學(xué)空天信息安全與可信計算教育部重點實驗室，湖北 武漢 430072)

第一寄存器小Qubit量子計算攻擊RSA研究

王寶楠1，陳宇航1，尹寶1，胡風1，張煥國2，王潮1

(1. 上海大學(xué)通信與信息工程學(xué)院特種光纖與光接入網(wǎng)省部共建教育部重點實驗室，上海 200072；2. 武漢大學(xué)空天信息安全與可信計算教育部重點實驗室，湖北 武漢 430072)

提出了針對RSA的小Qubit量子攻擊算法設(shè)計，量子攻擊的第一量子寄存器所需的Qubit數(shù)目由原先至少2L降低到L1，總體空間復(fù)雜度記為(L1, L)，其中2L1≥r，r為分解所得周期。由于第一寄存器量子比特數(shù)的減少，降低了算法復(fù)雜度和成功率，且改進原算法中模冪計算，提升運算速率。改進攻擊算法的量子電路的時間復(fù)雜度為T=O(2L2)。在時間復(fù)雜度和空間復(fù)雜度上都有明顯的進步。改進算法的成功率降低了，但實際成功求解時間，即每次分解時間/成功率，依然低于Shor算法目前的主要改進算法。完成了仿真模擬實驗，分別用11、10、9 Qubit成功分解119的量子電路。

Shor算法；RSA算法；量子電路；小比特；攻擊

1 引言

《Nature》[1]在調(diào)查歐洲、美國多個量子中心后，判斷破譯現(xiàn)有的1 024 bit RSA密碼所需要的千位Qubit以上的通用量子計算機，在未來5～10年內(nèi)仍難實現(xiàn)。

根據(jù)《Nature》[1]，Hanson和 Vandersypen等領(lǐng)導(dǎo)的荷蘭量子研究中心（QuTech Centre）的目標是近期研究17 Qubit。

瑞士蘇黎世聯(lián)邦技術(shù)研究所的Matthias Troyer[1]認為目前的通用量子計算機缺乏殺手級應(yīng)用，已知的2個應(yīng)用（密碼破譯和數(shù)據(jù)庫搜索）都不成功。Matthias Troyer還認為，百位Qubit不容易實現(xiàn)或者無法很經(jīng)濟地實現(xiàn)。Matthias Troyer對目前量子計算機的情況非常熟悉，還參加了南加州大學(xué)的加拿大量子計算機測試。

事實上，根據(jù)《Nature》，目前已經(jīng)實現(xiàn)的通用量子計算機最大規(guī)模為9 Qubit，由加州大學(xué)圣巴巴拉分校（UCSB）的John Martinis團隊實現(xiàn)，然而John Martinis認為通用量子計算機還在二戰(zhàn)時期第一臺電子計算機的程度。

盡管John Martinis團隊已經(jīng)在原理上驗證了Shor計算攻擊RSA的可行性，并在2011年成功用量子電路實現(xiàn)了量子傅里葉變換[2]，這是破譯RSA的量子計算Shor算法的核心基礎(chǔ)，2012年，John Martinis團隊還成功完成攻擊小規(guī)模RSA實驗[3]，分解了15=3×5。但是，John Martinis團隊不再繼續(xù)從事通用量子計算機的研究，2014年9月，John Martinis整個團隊全部搬入谷歌總部“建造能解決實際問題的量子計算機”——基于量子退火的專用量子計算機，其原理并不適合運用于公鑰密碼破譯的Shor算法。

因此需要考慮在通用量子計算機器件條件限制的情況下，研究公鑰密碼RSA的小Qubit量子計算攻擊方法，降低對通用量子計算機的器件要求[4]。

本文改進了原始Shor算法，提出新的量子電路設(shè)計，降低了量子器件要求，探究性地提出了小規(guī)模Qubit實現(xiàn)Shor算法對公鑰密碼的攻擊，并進行了仿真模擬。

本文介紹了Shor算法攻擊RSA的國內(nèi)外研究現(xiàn)狀，引出改進Shor量子算法對公鑰密碼的攻擊；給出Shor算法分解實驗。另外，本文分別給出Shor算法攻擊RSA的量子電路攻擊實驗和改進Shor量子攻擊算法實驗及運行結(jié)果；并進行了實驗分析；比較了目前主要的Shor改進算法，并對改進的Shor算法進行分析。

2 Shor算法攻擊RSA國內(nèi)外研究現(xiàn)狀

Shor算法對RSA的攻擊體現(xiàn)在Shor算法對RSA安全基礎(chǔ)的大數(shù)N的分解，關(guān)于Shor算法對N分解的研究一直是國內(nèi)外專家學(xué)者的研究熱點。

1996年，美國科學(xué)家Juan Pablo Paz在一個有干擾和損耗的量子電路上展示分解了15，理論上需要27 Qubit才能成功分解。同時他更是指出對于大數(shù)N，所需要的量子比特數(shù)是n=5L+7（其中L為不小于log2N的最小正整數(shù)）。這項工作的研究成果給實際操作中實現(xiàn) Shor量子算法提供了很好的借鑒。

2001年，斯坦福大學(xué)和美國IBM公司合作，利用核磁共振技術(shù)演示了Shor算法對整數(shù)15進行分解的實驗過程，但該實驗不能顯示其量子屬性，也無法擴展到更多的比特情況，限制了進一步的研究。

2004年，美國赫爾辛基理工大學(xué)的Vartiainen[5]利用約瑟夫森電荷構(gòu)成的量子比特實現(xiàn)了 Shor算法。他把Shor算法的量子電路分成了一系列2 Qubit和3 Qubit的量子門，不僅加速了Shor算法的實現(xiàn)，而且在此基礎(chǔ)上通過數(shù)值優(yōu)化的方法成功完成對 N=21分解的物理實現(xiàn)。但該實驗要求很高的物理性，即必須在特定的物理條件下才能實現(xiàn)。

2007年，法國理論物理研究實驗室在研究Shor算法的缺陷[8]（由量子比特間殘余耦合所造成）所產(chǎn)生的影響時，通過編寫Quantware庫并且調(diào)用該庫，用30個量子比特模擬實現(xiàn)了N=943的分解。該方法雖然很好理解，但是Quantware庫所用的限制性很多。2007年，中國科學(xué)院公布，中國科學(xué)技術(shù)大學(xué)潘建偉教授和楊濤教授等[9]與英國牛津大學(xué)的研究人員合作，在國際上首次利用光量子計算機實現(xiàn)了Shor量子分解算法，研究發(fā)表在2007年1月的物理評論快報上，并在該量子計算上成功操控 4個光子量子比特構(gòu)造一個簡單的線性光網(wǎng)絡(luò)，實現(xiàn) N=15的分解。

2010年，英國布里斯托大學(xué)電氣和電子工程物理實驗室和量子光學(xué)中心的Thompson等[10]介紹了基本的Shor因式分解量子算法實現(xiàn)過程，主要是在由6個H門和2個可控的相位門組成的波導(dǎo)電路中建立一個可以實現(xiàn)Shor量子分解算法的電路，并且成功地用Shor算法分解N=15。

2010年，解放軍信息工程大學(xué)通過改進量子傅里葉變換加速實現(xiàn)Shor算法對N的分解[11]，但該算法中改進的量子傅里葉變換是以串行代替并行加快速度的。該算法的空間復(fù)雜度記為（4，L），時間復(fù)雜度T=O(L3)。

2012年，美國加州大學(xué)圣巴巴拉分校的John Martinis[3]，在實現(xiàn)量子傅里葉變換電路基礎(chǔ)上，完成了15=3×5的素數(shù)分解實驗，原理上驗證了Shor計算攻擊RSA的可行性。

上述研究和最近的一些研究[12,13]都是 Shor算法分解N研究的代表，但基本上都需要在量子計算機器件[6,7]很高的要求下，包括需要千位量子比特的量子計算機和高精度的糾纏能力等。

3 改進Shor算法

3.1 改進Shor算法介紹

對大數(shù) N（N＞0）的素因子分解，也就是對大數(shù)N和整數(shù)x（x＜N）求出滿足同余式xr=1modN的階r。

改進Shor算法步驟如下。

Step1準備具有L1量子比特的第一寄存器和L量子比特的第二寄存器的態(tài)矢量其中，為周期。

Step2對第一寄存器實行 L1次 Hadamard變換得到到的個態(tài)的疊加，可給出

Step3將Ux,a算符應(yīng)用到寄存器，

Step4利用二進制查表法計算xamod N的值。如下[14]。

③ 當i≥0時，執(zhí)行④～⑩。

④ 如果ai=1，則執(zhí)行⑤～⑨。

⑤ 如果i≥k，則執(zhí)行⑥～⑧。

⑥ 把該位開始的 k個二進制數(shù)作為一個整體進行計算，進行連續(xù)k次平方。

⑧ 令i=i-k，減少一個分組的長度。

⑨ 如果i＜k，則把該位開始的k個二進制數(shù)作為一個整體，即令m=m×m×x mod N，且i=i-1。

⑩ 如果ai=0，則直接計算該位開始的k個二進制的平方取模，且i=i-1，最后返回m值。

Step5進行xamod N的階數(shù)搜索過程。

Step6對第一個量子寄存器進行 QFT逆變換，并觀測概率。

Step7由周期性求得階數(shù)r。

Step8由階數(shù)r求得2個N的分解數(shù)。

3.1.1 原始Shor算法分解N=119量子電路

圖1是理論上Shor算法的完整實現(xiàn)，第一量子寄存器需要的量子比特數(shù)第二量子寄存器需要的量子比特數(shù)

圖1 原始Shor算法分解N=119的量子電路

3.1.2 改進Shor量子算法分解N=119量子電路

基于改進Shor量子算法實現(xiàn)對RSA的攻擊量子電路原理如圖2所示。

圖2 改進的Shor小比特攻擊算法分解N=119的量子電路

對比圖1和圖2，改進的地方在于把第一量子寄存器的量子比特數(shù)1～14進行了減少，由原來的14 Qubit修改成了1～2的2個量子比特，與理論上相比少用了12個量子比特，這大大減少了對量子計算機的器件要求。

3.2 改進Shor量子算法分析

改進Shor算法相比原始Shor算法分析如下。

參考Shor算法及相關(guān)文獻[15]對Shor算法分解大數(shù)的理論分析，本文設(shè)計的量子電路主要包括3個部分：一是用一系列的H變換替換傅里葉變換；二是控制模冪變換，并引入二進制查表法計算模冪算法；三是量子傅里葉變換。

該改進 Shor量子算法主要是量子比特數(shù)的減少，一般情況下空間復(fù)雜度和時間復(fù)雜度與成功率呈相反的關(guān)系，即成功率的提升是以復(fù)雜度的提升為代價的。由于第一量子寄存器比特數(shù)的減少，所需通過H變換的次數(shù)也相應(yīng)地減少，引起了模冪中模乘次數(shù)的減少，促進了整個算法運行時間的減少，且并不影響后續(xù)的操作。第一量子寄存器執(zhí)行的是模冪操作的控制，是用于控制模冪運算的模乘次數(shù)和量子傅里葉變換，縮小了量子比特數(shù)，使所能進行的模冪運算次數(shù)也變少，并引發(fā)了后面操作次數(shù)的減少，在一定程度上降低了該Shor算法攻擊的成功率，但提高了成功求解速度。而引入二進制查表法的目的是進一步減少模乘的次數(shù)，該算法雖然增加了一點空間，但并不影響整體算法的空間復(fù)雜度，且引入該算法的主要目的是該算法能大幅度減少模冪中乘法的次數(shù)，使模冪的計算速度進一步提高。

Shor原始算法量子電路空間復(fù)雜度需要至少S=(2L, L)，L=log2N Qubit（第一量子寄存器需要2L Qubit，第二量子寄存器需要L Qubit，S表示空間復(fù)雜度）。改進Shor算法量子電路空間復(fù)雜度需要S=(L1, L)（第一量子寄存器需要L1 Qubit，第二量子寄存器需要L Qubit）。其中，L Qubit即進行模冪運算至少要有的量子比特數(shù)（保存模冪運算預(yù)運算的值）。L1 Qubit即量子傅里葉變換需要的量子比特數(shù)。例如，基于改進Shor算法分解N的步驟分析，設(shè)計的量子電路的量子比特數(shù)對于分解119的量子電路而言，從原來至少需要（14，7）量子比特降為僅用（2，7）量子比特。Shor原始算法量子電路計算復(fù)雜度，即時間復(fù)雜度為T=O(L3)，改進 Shor算法量子電路復(fù)雜度為T=O(L2)。

與 Shor算法相比，降低了至少 L規(guī)模的比特數(shù)，即空間復(fù)雜度降低了O(L)規(guī)模。與目前主要的Shor改進算法相比，改進Shor算法的比特數(shù)基本上與其他相近或更少，但是在成功求解時間上更小，且做法上更簡單，更易于理解。

由于現(xiàn)階段的通用量子計算機難以滿足破譯RSA公鑰密碼的實際需求，所以降低了成功率而使所需空間復(fù)雜度變低，能在一定程度內(nèi)解決量子計算機器件的難題，這樣做對目前更好地解決更大數(shù)的 RSA破譯有深遠的影響，所以值得推廣。正是應(yīng)用這一特點，提出了改進Shor量子攻擊方法。

3.3 改進Shor算法分解N=119量子電路的實驗

本實驗在配置為Intel Core2 Duo CPU T6670 2.20 GHz、內(nèi)存2 G的聯(lián)想筆記本上，在數(shù)學(xué)工具Mathematics9.0軟件下調(diào)用 José Luis Gómez-Mu?oz 和 Francisco Delgado編寫的量子程序包進行的量子電路上進行仿真。基于Shor算法實現(xiàn)步驟的分析，實驗成功分解了15、21、35、65、119、123、205等數(shù)，下面討論Shor算法量子電路[15]實現(xiàn)分解N=119的實驗。

將改進Shor量子攻擊算法與原Shor算法進行對比實驗，比較其攻擊結(jié)果。選用Shor算法分解 N=119的實驗，選擇的隨機數(shù) x=13，在Mathematics 9.0軟件下進行仿真實驗。

運行如圖2所示的量子電路，求解所得周期，結(jié)果如圖3所示。

圖3 量子傅里葉變換后第一寄存器|c＞的概率（第二寄存器的

由此得到N=119，可以分解為119=17×7。

這里要說明的是，在判斷周期r的時候，其實只要觀察圖3的波峰即可確定。在判斷時，直接觀察波峰數(shù)就是周期數(shù)的依據(jù)是：結(jié)合最后測量的概率公式，在觀察的概率分布時，s=1,…,r-1，c的取值為k，當出現(xiàn)一個k滿足時，離散概率就出現(xiàn)一個波峰。

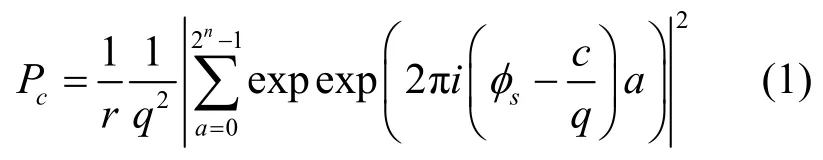
本次實驗的其他結(jié)果統(tǒng)計如表1～表4所示。

表1 分解相同數(shù)、相同比特數(shù)，不同隨機數(shù)下的實驗結(jié)果

表2 分解相同數(shù)、相同隨機數(shù)13，不同比特數(shù)下的實驗結(jié)果

表3 分解相同數(shù)，相同隨機數(shù)83，不同比特數(shù)下的實驗結(jié)果

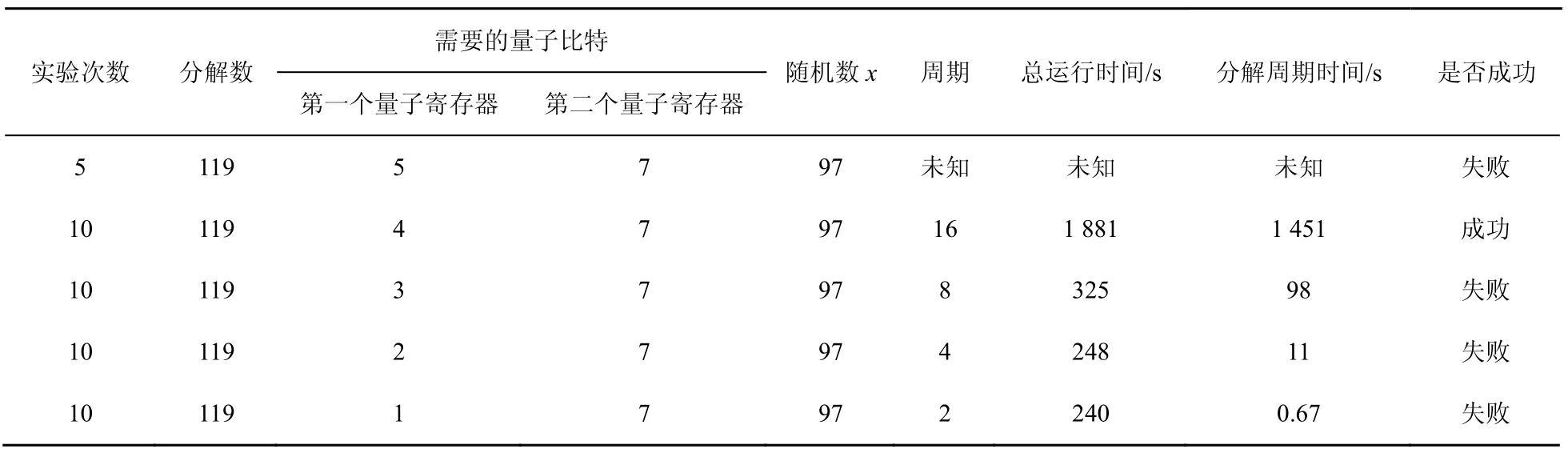
表4 分解相同數(shù)、相同隨機數(shù)97，不同比特數(shù)下的實驗結(jié)果

觀察表1可發(fā)現(xiàn)，不同隨機數(shù)會影響分解運行時間。

由表2～表4可以發(fā)現(xiàn)，量子比特數(shù)的多少對運行時間是有影響的，且隨機數(shù)的選擇對量子比特數(shù)的多少也是有影響的。

4 實驗分析

4.1 成功率分析

分解 119，在設(shè)置不同量子比特數(shù)、不同隨機數(shù)下，實驗成功次數(shù)的統(tǒng)計如表5所示。

觀察表5可以發(fā)現(xiàn)，當量子比特數(shù)減少時，對于分解的成功率是有影響的，且可以定性地反映出當量子比特數(shù)減少時，成功率是下降的。

Shor原始算法給出，選定一個隨機數(shù)求得周期r的成功率為，其中r是階也可以說是周期，歐拉函數(shù)，p和q是N的2個因子。因為數(shù)論上有，k是一個小于1的常數(shù)。所以，Shor認為如果重復(fù)做O(loglogr)規(guī)模次，其成功率一定可以增加。由于本文的改進Shor算法與Shor算法本質(zhì)上是一樣的，所以成功求得周期r的概率也是。如果知道周期 r，則可成功分解的概率至少是，即Shor算法成功分解的概率至少是。結(jié)合實驗數(shù)據(jù)，給出成功率公式為

其中，φ(N)、φ(r)都是關(guān)于N和r的歐拉函數(shù)，N是要分解的數(shù)，r是求的階，即周期。所以在分解119的時候，當L=2，r=4時，成功率為

1997年，Eicher J和Opoku Y的研究給出了一個在多項式時間內(nèi)以1/480≈0.002的成功率攻擊橢圓曲線離散對數(shù)問題的量子計算算法，證明低成功率也可以成功攻擊。而這里分解 119，成功率為0.001 3，所以也滿足條件。

4.2 復(fù)雜度分析

一個量子電路的復(fù)雜度分為空間復(fù)雜度和時間復(fù)雜度，具體反映在3個方面：量子電路比特數(shù)[16]、量子電路需要的基本量子門規(guī)模（也稱量子電路尺寸）和量子電路深度。量子電路尺寸和量子電路深度對應(yīng)量子電路所需要的時間規(guī)模，即時間復(fù)雜度，量子比特數(shù)目即空間復(fù)雜度。電路尺寸是指一個量子電路中所有基本量子門電路的總數(shù)，基本量子門指的是H門、CNOT門、控制-旋轉(zhuǎn)門、Toffli門等。一個量子電路的深度是指該量子電路所有量子門的深度之和，直觀上講就是這個量子電路有幾層，類似于程序的循環(huán)。總之，在計算量子電路復(fù)雜度時，一要計算該量子電路需要的量子比特數(shù)，即空間復(fù)雜度；二是計算量子電路所需要的基本量子門規(guī)模和量子電路的深度，即量子電路的時間復(fù)雜度。

由于算法本質(zhì)上還是Shor算法的原型，下面給出改進Shor算法的復(fù)雜度。因為Shor算法主要由量子傅里葉變換和模冪運算組成，故 Shor算法的復(fù)雜度也是指這兩部分的復(fù)雜度，如表6所示。

表6 Shor算法復(fù)雜度

表6中的L=log2N，N為要分解的數(shù)。

引入二進制查表法加快了模冪算法的運算速度。在改進的Shor算法引入該算法后，其空間復(fù)雜度和時間復(fù)雜度依然為（L1，L）和T=O(2L2)。

4.3 算法比較

4.3.1 與原始Shor攻擊算法比較

通過分解119實驗，總結(jié)改進Shor量子算法屬性，并與原始Shor算法進行比較，如表7所示。其中，L1為第一量子寄存器量子比特數(shù)，L=log2N。

可以知道，改進Shor算法成功求解時間相對于 Shor原始算法成功求解時間可簡化為Shor原始算法成功求解時間可簡化為，所以，改進Shor算法成功求解時間小于原始算法，得到了一定的提升。

表7 改進Shor量子算法與原始Shor算法的比較

雖然降低了成功率，但也成功降低了復(fù)雜度，在分解119的時候，成功地將所需空間復(fù)雜度從S=(2L，L)降低為S=(2，L)。這對于現(xiàn)階段還沒有通用的大量子比特計算機來說具有深刻的意義，復(fù)雜度降低，讓其可以在更少量子比特數(shù)的量子計算機上運行，能很好地解決現(xiàn)階段量子計算機器件要求高的難題。

4.3.2 與目前主要改進Shor算法比較

2008年，英國倫敦帝國學(xué)院布萊克特實驗室的Parker S等[17]給出了一個單一的純量子比特與log2N量子比特在任意混合態(tài)下的集合來有效實現(xiàn)Shor因式分解的算法。該算法大大減少了所需的量子比特數(shù)。

2010年，解放軍信息工程大學(xué)[11]提出了2個新的改進Shor算法：具有高概率的整數(shù)分解量子計算算法和 Shor整數(shù)分解量子算法的加速實現(xiàn)算法。

具有高概率的整數(shù)分解量子計算算法指出需要3個L bit的量子寄存器實現(xiàn)（該量子電路需要4次量子傅里葉變換和1次模冪運算）。

Shor整數(shù)分解量子算法的加速實現(xiàn)算法指出需要S=(4, L)量子比特（每個量子傅里葉變換需要2個量子比特，第一量子寄存器對應(yīng)量子傅里葉變換需要4個量子比特，第二個量子寄存器需要L Qubit）。

2013年，美國的佐治亞大學(xué)[18]用8 Qubit實現(xiàn)了Shor算法分解51和85的實驗，它是對量子輸入態(tài)的改進，該算法指出第一量子寄存器和第二量子寄存器都只需要 S=(Lmax, Lmax) Qubit，其中，接近為

由表8可知，改進Shor算法的復(fù)雜度比文獻[11]的2個改進Shor整數(shù)分解算法要小。Shor整數(shù)分解量子算法的加速實現(xiàn)算法的第一量子寄存器量子比特數(shù)雖然比較小，但所需的時間復(fù)雜度還是O(L3)，相對于改進Shor算法，雖然減少了量子比特數(shù)，但是時間復(fù)雜度多了L倍，所以第一量子比特數(shù)降低為4沒有很大的意義。而具有高概率的整數(shù)分解量子計算算法增加了量子比特數(shù)，且時間復(fù)雜度還是O(L3)。這里定義一個新的時間——成功求解時間，即每次求解時間與成功率之間的比值。可知，改進Shor算法成功求解時間相對于文獻[11]的2個改進Shor整數(shù)分解算法的成功求解時間可簡化為文獻[11]的 Shor整數(shù)分解算法成功求解時間可簡化為O(L3)4，文獻[11]的具有高概率的 Shor分解算法成功求解時間簡化為L越大，復(fù)雜度一個級別的差距不是與幾個簡單的自然數(shù)相乘就可以達到的，因此可知改進Shor算法的成功求解時間小于文獻[11]的2個改進Shor整數(shù)分解算法的成功求解時間。

表8 改進Shor量子算法與目前主要的改進Shor算法的比較

對比Michael[18]的改進Shor算法，改進Shor算法的復(fù)雜度比 Michael的復(fù)雜度要小，且成功求解時間比改進Shor算法的成功求解時間大。對比Parker的改進Shor算法，改進Shor算法的時間復(fù)雜度較小，空間復(fù)雜度相近，最主要的是，成功求解時間比Parker改進Shor算法的成功求解時間小。

5 結(jié)束語

本文的主要內(nèi)容在于犧牲成功率來換取空間復(fù)雜性的降低，并在一定范圍內(nèi)提高了算法的運算速度，目的是為了在現(xiàn)有量子計算機器件允許的條件下開展研究，事實上并沒有降低實際上的成功求解時間。

雖然犧牲了成功率，需要數(shù)百次運行才能得到成功的破譯結(jié)果，但降低了對通用量子計算機的器件要求，提高了通用量子計算機破譯公鑰密碼的現(xiàn)實性。改進的模冪計算也提高了Shor算法的運算速度。

由于實際成功求解時間等于每次分解時間除以成功率。本文提出的小Qubit改進Shor算法，實際成功求解時間還是低于 Shor算法和目前主要的改進Shor算法。

就算法本身而言，雖然Shor算法能夠?qū)崿F(xiàn)把指數(shù)級的運算降為多項式時間內(nèi)來完成[19]，但其需要的資源卻隨著量子比特數(shù)指數(shù)級增長。理論上講，當量子比特數(shù)增加時，量子算法的能力應(yīng)該是更強的，因為量子比特數(shù)增加了，并行計算的資源增加了，那么利用并行計算的量子算法自然增強了。但事實上，當量子比特數(shù)增加時，消耗資源的增長反而限制了量子算法的實現(xiàn)，使量子算法陷入一個無法掙脫最開始并行的境地。由此，本文也驗證了在通用量子計算機還沒有達到千位量子比特之前，想要利用更多量子比特并行能力的想法目前還不能實現(xiàn)。

這就是說，盡管大家都認為多量子比特可能比小量子比特實現(xiàn)量子算法解決實際問題更好，但是當器件進展尚無法控制千位量子比特時，不能達到預(yù)期的效果。所以本文改進算法的研究有助于充分提高現(xiàn)有小通用量子計算機破譯公鑰密碼的可行性。

[1] GIBNEY E. Physics: quantum computer quest: after a 30-years struggle to harness quantum weirdness for computing, physicists finally have their goal reach[J]. Nature News Feature, 2014:24-26.

[2] MARIANTONI M, WANG H, YAMAMOTO T et al. Implementing the quantum von neumann architecture with superconducting circuits[J]. Science, 2011, 334(6052):61-5.

[3] ERIK L, BAREDNS R., CHEN Y, et al. Computing prime factors with a josephson phase Qubit quantum processor[J]. Nature Physical, 2012, 8: 719-723

[4] 王潮, 王云江, 胡風. 量子計算機的商業(yè)化進展及對信息安全的挑戰(zhàn)[J]. 網(wǎng)絡(luò)與信息安全學(xué)報, 2016, 2(3):17-27.WANG C, WANG Y J, HU F. Shaping the future of commercial quantum computer and the challenge for information security[J]. Chinese Journal of Network and Information Security, 2016, 2(3):17-27.

[5] VARTIAINEN J J, NISKANEN A O, NAKAHARA M, et al. Implementing Shor's algorithm on Josephson charge Qubits[J]. Physical Review A, 2004, 70(1).

[6] GLENDINNING I, ?MER B. Parallelization of the QC-Lib quantum computer simulator library[J]. Lecture Notes in Computer Science, 2003, (3019):461-468.

[7] DE-RAEDT K, MICHIELSEN K, DE-RAEDT H ET AL. Massively parallel quantum computer simulator[J]. Computerphysicscommunications,2007,176:121-136.

[8] GARCíA-MATA I, FRAHM K M, SHEPELYANSKY D L. Effects of imperfections for Shor’s factorization algorithm[J]. Physical Review A, 2007,(75).

[9] YANG C, DANIEL L, BROWNE E, YANG T, et al. Demonstration of a compiled version of Shor’s quantum factoring algorithm using photonic Qubits[J]. Physical Review Letter, 2007, (99).

[10] THOMPSON M G, POLITI A, MATTHEWS J C F, et al. Integrated waveguide circuits for optical quantum computing[J]. Institution of Engineering and Technology, 2011, 5: 94-102

[11] 付向群, 鮑皖蘇. 具有高概率的量子計算算法研究[D]. 鄭州:解放軍信息工程大學(xué). 2011 FU X Q, BAO W S. Research on the quantum algorithm with high probability[D]. Zhengzhou: PLA Information Engineering University. 2011

[12] NAGAICH S, GOSWAMI Y C. Shor’s algorithm for quantum numbers using MATLAB simulator [C]//The fifth International Conference on Advanced Computing amp; Communication Technologies. 2015:165-168.

[13] DAVID S W, CHARIES D H, LLOYD C L, et al. Simulatiobs of shor’s algorithm using matrix product states[J]. 2015.

[14] 董付國, 厲玉蓉, 杜萍. 方冪模快速計算的二進制分組查表法[J].計算機工程與應(yīng)用, 2009, 45(22): 71-73.DONG F G, LI Y R, DU P. Fast calculation of modular exponentiation binary group look-up table method[J]. Computer Engineering and Applications, 2009, 45(22): 71-73.

[15] 佐川弘幸, 吉田宣章, 著. 宋鶴山 譯. 量子信息論[M]. 大連:大連理工大學(xué)出版社, 2007.SONG H S. Quantum information theory[M]. Dalian: Dalian University of Technology Press, 2007.

[16] CHOI B S, METER R V. On the effect of quantum interaction distance on quantum addition circuits[J]. ACM Journal on Emerging Technologies in Computing Systems. 2010.

[17] PARKER S, PLENIO M B. Efficient factorization with a single pure Qubit and log N mixed qubits[J]. Physical Review Letter, 2000,(85): 3048-3052

[18] MICHAEL R.G, ZHOU Z Y. Factoring 51 and 85 with 8 Qubits[R].Scientific Reports, 2013.

[19] 孫國棟, 蘇盛輝, 徐茂智.求根問題的量子計算算法[J].北京工業(yè)大學(xué)學(xué)報, 2015, (41): 366-371.SUN G D, SU S H, XU M Z. Quantum computing algorithms of find roots problems[J]. Journal of Beijing University of Technology,2015, (41): 366-371.

Research of the small Qubit quantum computing attack to the RSA public key cryptography

WANG Bao-nan1, CHEN Yu-hang1, YIN Bao1, HU Feng1, ZHANG Huan-guo2, WANG Chao1

(1. Key Laboratory of Special Fiber Optics and Optical Access Networks, School of Communication and Information Engineering, Shanghai University, Shanghai 200072, China;2. Key Laboratory of Aerospace Information Security and Trusted Computing, Wuhan University, Wuhan 430072, China)

The small Qubit quantum algorithm attack to RSA was proposed, the need Qubit of the first quantum register from 2L to L1, it can be reduced to 2 Qubit, the overall space complexity denoted (L1,L), where 2L1≥r, r is the period of decomposed. Because of the reduce of the first quantum register, it reduces the algorithm’s complexity and success rates, and use the binary look-up table method to compute the modular exponentiation, it enhances the computing speed. The improved algorithm’s quantum circuit complexity is T=O(2L2). It have a significant improvement on the time complexity and space complexity. Although the success rate is reduced, the overall success solution time is still lower than the Shor algorithm and the current major improvements Shor algorithm. Completed a simulation experiment. Respectively use the 11、10、9 Qubit decomposing the quantum circuit 119. The new algorithm explore the reality of using a universal quantum computer device to decipher the public key cryptography.

Shor algorithm, RSA algorithm, quantum circuits, small qubits, attack

s：The Key Program of National Natural Science Foundation of China (No.61332019), The National Natural Science Foundation of China (No.61572304, No.61272096, No.60970006)

TP309

A

10.11959/j.issn.2096-109x.2017.00206

2017-08-19；

2017-09-27。

王潮，wangchao@staff.shu.edu.cn

國家自然科學(xué)基金重點資助項目（No.61332019)；國家自然科學(xué)基金資助項目（No.61572304, No.61272096,No.60970006）

王寶楠（1989-），女，江蘇淮安人，上海大學(xué)博士生，主要研究方向為信息安全、量子計算密碼、社會網(wǎng)絡(luò)。

陳宇航（1991-），男，浙江杭州人，上海大學(xué)碩士生，主要研究方向為量子計算與量子攻擊密碼分析。

尹寶（1991-），男，河南信陽人，上海大學(xué)碩士生，主要研究方向為量子計算與量子攻擊密碼分析。

胡風（1991-），男，浙江溫州人，上海大學(xué)博士生，主要研究方向為信息安全、量子計算密碼、社會網(wǎng)絡(luò)。

張煥國（1945-），男，河北元氏人，武漢大學(xué)教授、博士生導(dǎo)師，主要研究方向為信息安全、密碼學(xué)和可信計算。

王潮（1971-），男，江蘇鎮(zhèn)江人，博士，上海大學(xué)教授，主要研究方向為無線傳感器網(wǎng)絡(luò)、網(wǎng)絡(luò)信息安全與橢圓曲線密碼學(xué)、量子計算與量子攻擊密碼分析。