組合飛行器姿態跟蹤的自適應模糊無源控制

楊思亮 李羅鋼 莊學彬 孫 光

中國運載火箭技術研究院研究發展中心，北京100076

組合飛行器姿態跟蹤的自適應模糊無源控制

楊思亮 李羅鋼 莊學彬 孫 光

中國運載火箭技術研究院研究發展中心，北京100076

以組合飛行器為研究對象，介紹了組合飛行器在軌服務期間的姿態跟蹤控制。利用無源性(輸入輸出穩定性)控制理論和自適應模糊邏輯系統設計了一種自適應控制方案，該方案利用飛行器的動力學特性以及模糊邏輯系統的萬能逼近能力，使得所設計的控制器對飛行器的模型不確定性和外部環境力矩具有很強的自適應性和魯棒性。

組合飛行器；無源性控制；模糊控制

航天器在軌服務技術將是航天器技術最重要的發展方向之一。在未來，對航天器的在軌裝配、在軌維護和后勤支持等服務，能像今天對汽車的維修與加油那樣變成常規操作，將意味著航天器技術本身走向了成熟，人類將成為更廣闊宇宙空間的主人[1]。

組合體控制能力是實現在軌服務臨近操作的關鍵，首先要捕獲目標，為實施操作創造條件，然后還要為操作過程創造穩定的平臺基礎。捕獲目標后的操控平臺，質心和慣量特性發生了較大變化，盡管通過動力學參數的在軌辨識可以在一定程度上獲得模型參數，但由于各種復雜因素的存在，系統仍具有較大的參數不確定性，同時在平臺操控過程中也受到各種未知干擾。這些特性對組合體控制器的設計提出了較高要求，需要設計出不依賴系統精確模型和對外干擾具有良好魯棒性的控制方法，才能使組合體飛行器實現快速穩定的姿態控制。

模糊控制是一種有效的處理不確定系統的非線性智能控制方法，Richard和Jyh-Shing[2]設計了用于Cassini土星探測器的模糊姿態控制器，并且和Bang-Bang控制相比較，結果表明了模糊控制器在跟蹤控制、推進器開/關時間控制等方面的優越性。此外，針對NASA的FAST(Fast Auroral Snapshot Explorer)航天器也進行了姿態模糊控制研究[3]。預測控制是具有模型預測、滾動優化和反饋校正功能的控制算法，因其具有良好的控制效果而得到廣泛的應用，被控對象已從線性系統擴展到非線性系統。為進一步減少預測控制在線計算量以適用于快變的非線性被控對象，近年來對具有封閉解析形式的非線性廣義預測控制律的研究被極大地關注。文獻[4]對光滑仿射非線性控制系統利用當前輸出的各階導數構造未來輸出的Taylor級數預測模型，導出了以預測輸出跟蹤誤差范數最小為指標的廣義預測控制解析解，并計算出不同系統相對階和控制階數下閉環系統穩定表，很好地解決了用高的控制階數提高輸出預測精度的問題。預測控制和模糊控制都是控制不確定系統的有效方法，實踐證明將2者合理結合可進一步提高不確定系統的控制效果[5-6]。文獻[7-8]通過將控制量和姿態加速度引入性能指標，利用模糊邏輯系統和廣義預測控制相結合的辦法對飛行器姿態跟蹤系統分別設計了直接和間接自適應模糊預測控制器，均取得了較好的控制效果，但是模糊控制規則數目相對巨大，使所設計的控制器難以實際應用。為了更好的完成在軌服務組合飛行器的姿態控制任務，本文在文獻[8]的基礎上，針對飛行器姿控系統提出了一種結合無源性和模糊控制方法的控制器設計方法，所設計的控制器對飛行器的模型不確定性和外部干擾力矩具有很強的自適應性和魯棒性，并且巧妙的避免了因模糊規則數目大而需要在線更新計算自適應參數的負擔，使設計的控制器更具有實用價值。

1 預備知識

1.1 模糊邏輯系統

自適應模糊邏輯系統采用的規則庫形如[9]：

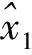
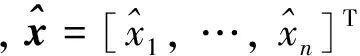
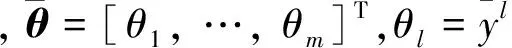
1.2 輸入輸出系統

引理1[10]對輸入輸出系統

e(s)=W(s)r(s)

式中，e(s),r(s)為n維向量e(t),r(t)的拉普拉斯變換，W(s)∈Rn×n(s)。若W(s)是嚴格正則且指數穩定的，則當r(t)∈L2∩L∞時有

1)e(t)∈L2∩L∞；

3)e(t)在R+上一致連續；

4)當t→∞時，e(t)→0。

引理2[10]若1≤plt;∞，則當g(t)∈Lp，且g(t)在R+上一致連續時有

g(t)→0， (t→∞)。

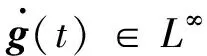
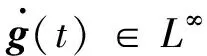
g(t)→0， 當t→∞。

2 問題描述

本文采用歐拉角描述的飛行器運動學方程，即角速度ω在星體坐標系中的表達式近似為：

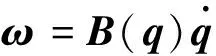
(1)

式中，q=[φ,θ,ψ]T,為飛行器在軌道坐標系中的滾動角φ、俯仰角θ和偏航角ψ，而飛行器姿態動力學方程為：

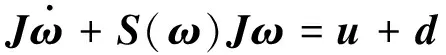
(2)

式中，J為轉動慣量矩陣，u為控制力矩，d為干擾力矩，S(p)為向量p=[p1,p2,p3]T的反對稱矩陣：

假設慣性張量陣J、干擾力矩d和期望軌跡qr(t)滿足如下條件：

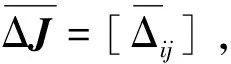
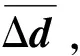
3)qr(t)及其各階導數均有界。

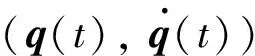
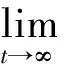
3 模型精確時控制器設計

3.1 控制器設計

將式(1)代入(2)可知，飛行器的姿態動力學方程為

(3)

對于飛行器姿態動力學方程式(3)，具有以下性質：

性質1 矩陣H(q)=BTJB是正定對稱陣；

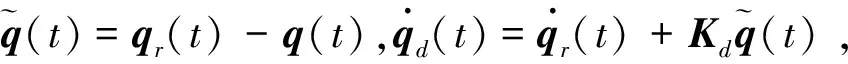
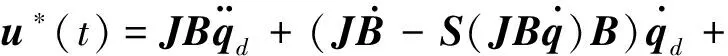
(4)

式中，Kp是正定矩陣。將其代入飛行器姿態動力學方程式(3)，得到閉環系統誤差方程為：

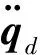
(5)

與一些經典的反饋控制方案不同，該控制律得到的閉環系統方程是一個關于誤差的非線性微分方程。若令r=[r1,r2,r3]T那么則上述方程可寫為更加緊湊的形式

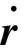
(6)

3.2 穩定性分析

在控制律(4)作用下，有如下結論：

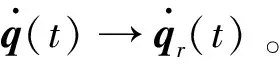
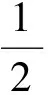
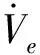
(7)

這表明沿閉環系統軌跡Ve(t)是單調有界的，故當t→∞時，Ve(t)存在有限極限Ve(∞)，且對任意的t≥t0≥0有

0≤Ve(∞)≤Ve(t)≤Ve(t0)lt;∞。

結合上式及V1(t)的定義可知，對任意的t≥t0≥0有

所以r∈L∞。又由式(7)可知

對上式兩邊從t0→∞積分可得

所以r∈L2。

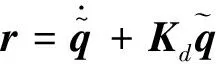
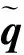
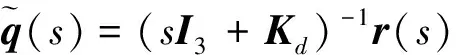
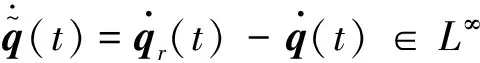
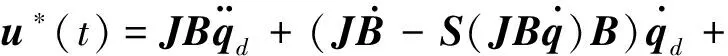
由飛行器姿態動力學方程可知：

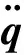
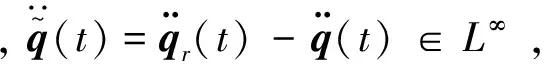
4 模型中含不確定時自適應控制器設計

由于被控對象中存在模型不確定和未知外干擾，所以控制器式(4)不能實現。考慮設計另一控制律來補償控制律式(4)中未知項的影響，以達到所施加的控制逼近理想控制律式(4)。

利用關于J和d的假設條件1)和2)將控制律式(4)寫為：

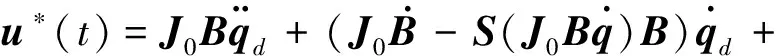
(8)

式中：

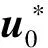
考慮將控制律取為

(9)

將式(9)代入飛行器姿態動力學方程式(3)，得到閉環系統誤差方程為：

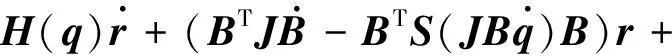
(10)

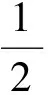
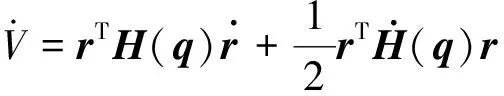
(11)

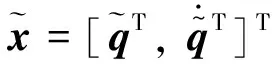
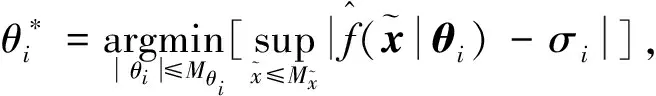
(12)

最優模糊控制器

以及最小近似誤差

(13)

那么σ用模糊邏輯系統逼近可以寫為

(14)

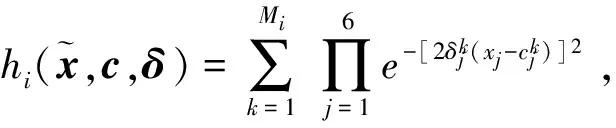
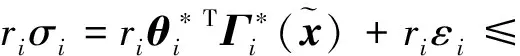
(15)

其中

(16)

因此

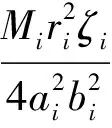
(17)

式(11)可寫為

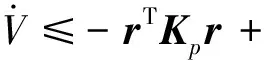
(18)

選取控制律u1(t)為

(19)

式(18)變為

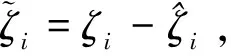
(20)

式中，γi為大于0的常數。將V1沿誤差系統式(10)求導可得

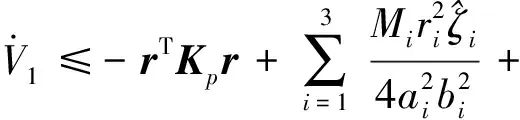
(21)

(22)

式中，ki為正常數。根據式(21)和(22)，上述李雅普諾夫函數的導數可化簡為：

(23)

通過以上自適應控制設計，很容易得到如下的結論。

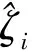
5 仿真研究

設飛行器姿態運動學模型(1)中矩陣B(q)為：

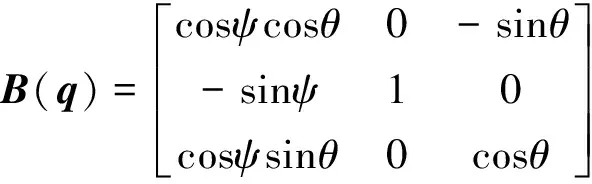
已知飛行器慣性張量陣的標稱值J0及干擾標稱值d0分別為：

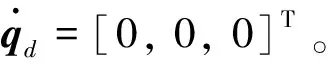
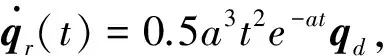
仿真時假設慣性張量陣J和所受干擾d分別為：

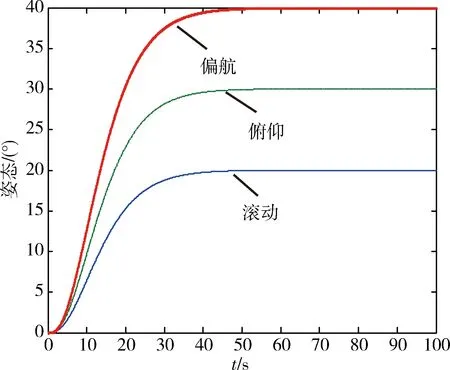
圖1 飛行器姿態

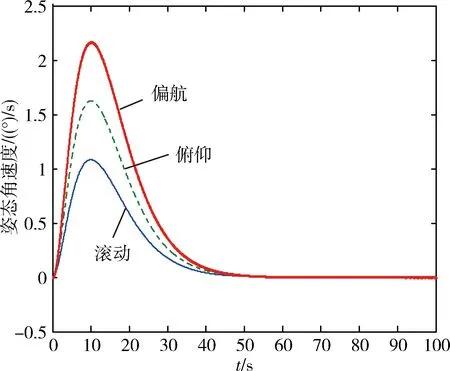
圖2 飛行器角速度

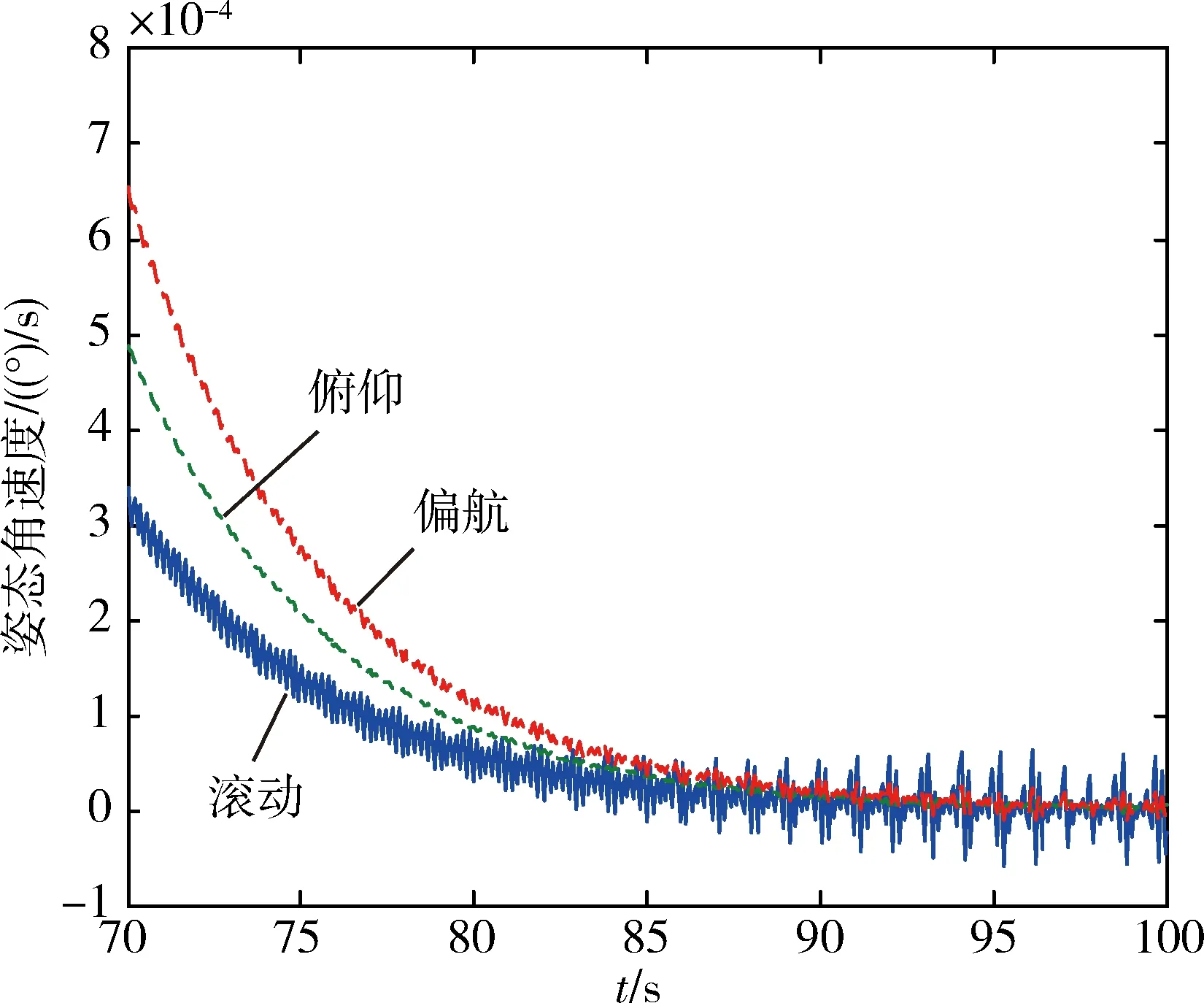
圖3 70s后的飛行器姿態穩定度

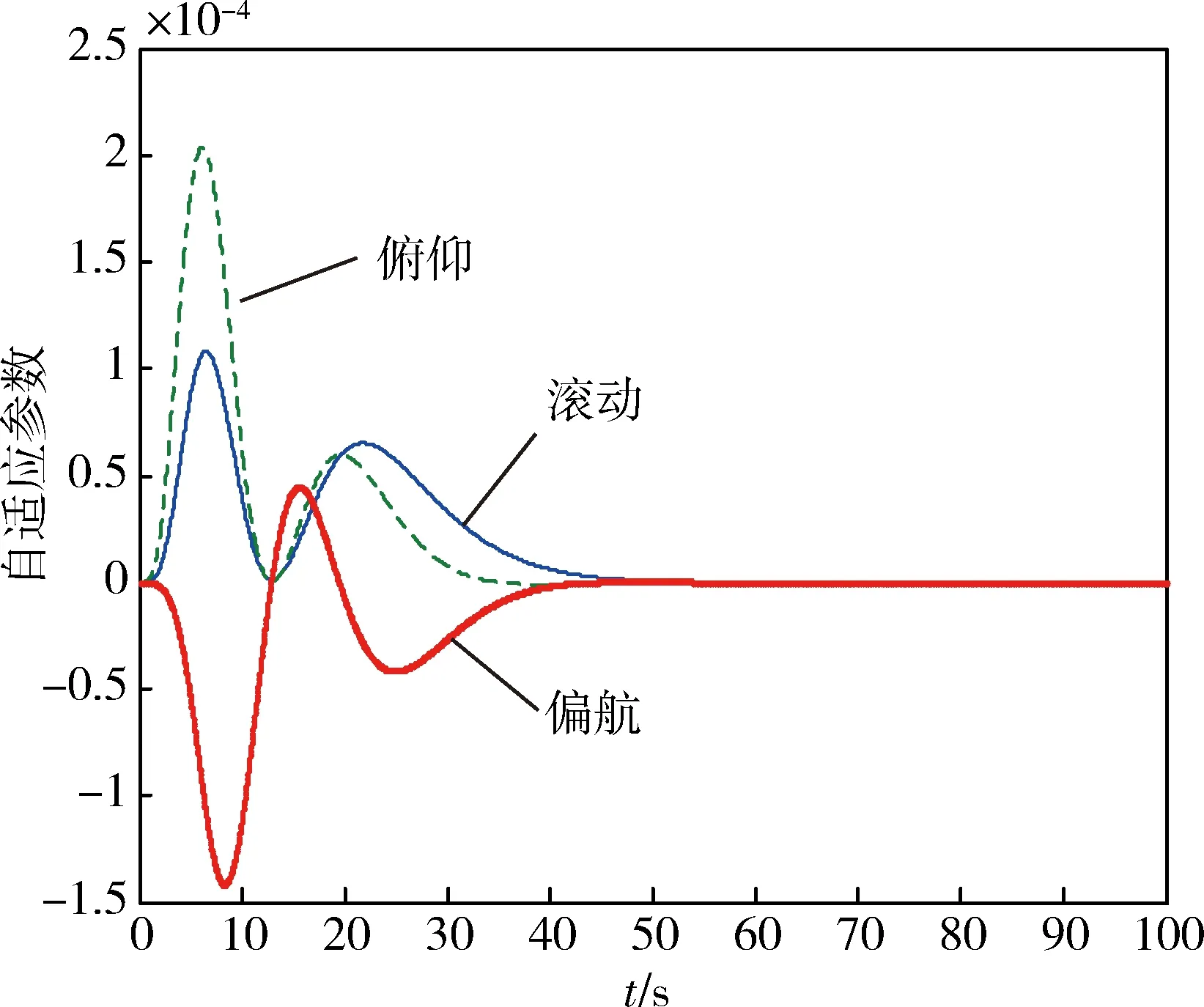
圖4 參數自適應律

從仿真結果可以看出，盡管模型中存在較大的不確定性和未知外部干擾，但利用本文所設計的自適應無源控制律能使飛行器姿態角和姿態角速度很快跟蹤到期望的姿態角和姿態角速度，并且具有良好的控制精度、較高的穩定度以及較強的魯棒性。

6 結論

在飛行器模型存在不確定性和未知外干擾時，基于輸入輸出穩定性理論(無源性)和模糊邏輯系統理論研究了飛行器姿態跟蹤控制問題，充分利用飛行器的動力學特性設計了一種非線性模糊自適應控制器。在設計過程中，采用對模糊邏輯系統中的參數范數進行自適應方式，避免了因模糊規則數目大而需要在線更新計算自適應參數的負擔。顯然，上述處理方式使所設計的控制方案更具有實際應用性。同時，仿真結果也顯示了閉環系統是穩定的，輸出跟蹤效果是令人滿意的。

[1] 陳小前, 袁建平, 姚雯, 趙勇. 航天器在軌服務技術[M]. 北京：中國宇航出版社，2009.

[2] Richard Y Chiang, Jyh-Shing Jang. Fuzzy Logic Attitude Control for Cassini Spacecraft[C]. IEEE World Congress on Computational Intelligence, Orlando,Florida,1994:1532-1537.

[3] Woodard M A. Fuzzy Open-loop Attitude Control for the FAST Spacecraft[EB/OL]. NASA Web Server at http://fdd.Gsfc.Nasa.Gov/Mwoodard/Aiaa96/Aiaa96.html, Goddard Space Flight Center, Greenbelt,MD,1996.

[4] Chen W H, Balance D J, Gawthrop P J. Optimal Control of Nonlinear Systems: A Predictive Control Approach[J]. Automatica, 2003, 39(4): 633-641.

[5] 張春良, 梅德慶, 陳子辰. 微制造隔振平臺振動的模糊廣義預測控制[J]. 機械工程學報, 2007, 43(12): 194-202. (Zhang Chunliang, Mei Deqing, Chen zichen. Fuzzy Generalized Predictive Ccontrol of Microvibration Isolation System For A Micro-manufacturing Platform[J]. Chinese Journal of Mechanical Engineering, 2007, 43(12): 194-202.)

[6] 師五喜, 霍偉, 吳宏鑫. 柔性關節微操作機器人自適應模糊預測控制[J]. 動力學與控制學報, 2003, 1(1): 84-89. (Shi Wuxi, Huo Wei, Wu Hongxin. Aaptive Fuzzy Predictive Control of A Micromanipulator with Flexible Joints[J]. Journal of Dynamics and Control, 2003, 1(1): 84-89.)

[7] 孫光, 霍偉. 衛星姿態直接自適應模糊預測控制[J]. 自動化學報, 2010, 36(8): 1151-1159. (Sun Guang, Huo Wei. Direct Adaptive Fuzzy Predictive Control of Satellite Attitude[J]. Acta Automatica Sinica, 2010, 36(8): 1151-1159.)

[8] 孫光, 霍偉. 衛星姿態跟蹤的間接自適應模糊預測控制[J]. 系統科學與數學, 2009, 29(10): 1327-1342. (Sun Guang, Huo Wei. Indirect Adaptive Fuzzy Predictive Control for Satellite Attitude Tracking[J]. Journal of Systems Science and Mathematical Sciences, 2009, 29(10): 1327-1342.)

[9] 王立新. 自適應模糊系統與控制—設計與穩定性分析[M]. 北京: 國防工業出版社, 1995. (Wang Lixin. Adaptive Fuzzy System and Control-Design And Stability Analysis[M]. Beijing:National Defence Industry Publishing Company,1995.)

[10] Desoer C A , Vidyasager M.. Feedback System: Input-output Properties [M]. New York: Academic Press, 1975.

[11] Li Ping, Yang Guanghong. A New Adaptive Control Approach for Nonlinear Strict-feedback Systems Using Nonlinearly Parameterized Fuzzy Approximators[J]. International Journal of Systems Science, 2011, 42(3): 517-52.

AdaptiveFuzzyPassiveControlforAttitudeTrackingofCombinationSpacecraft

Yang Siliang， Li Luogang， Zhuang Xuebin， Sun Guang

China Academy of Launch Vehicle Technology Ramp;D Center, Beijing 100076, China

Combinationspacecraftistheresearchgoalandtheattitudetrackingcontrolofcombinationspacecraftduringon-orbitservicingisintroducedinthispaper.Anadaptivecontrolschemeisdesignedbasedonpassive(input-outputstability)controltheoryandadaptivefuzzylogicsystem.Thiscontrolsystemmakesuseofthedynamiccharacteristicsofspacecraftandtheuniversalapproximationoffuzzylogicsystem,therefore,thedesignedcontrollerhasgoodadaptabilityandrobustnessforthemodeluncertaintyofspacecraftandtheexternalenvironmentmomentum.

Combinationspacecraft；Passivity-basedcontrol；Fuzzycontrol

V488.2

A

1006-3242(2017)04-0042-06

2016-03-10

楊思亮(1983-)，女，陜西綏德人，博士，主要研究方向為飛行器動力學與控制；李羅鋼(1984-)，男，山東淄博人，博士，主要研究方向為制導控制技術；莊學彬(1983-)，男，福建泉州人，博士，主要研究方向為制導控制技術；孫光(1980-)，男，山東人，博士，主要研究方向為姿態控制技術。