高中數學中的數形結合思想的論述
王 芳
(江蘇省南京市高淳區湖濱高級中學,江蘇 南京 211300)
高中數學中的數形結合思想的論述
王 芳
(江蘇省南京市高淳區湖濱高級中學,江蘇 南京 211300)
數形結合的思想是高中重要思想方法之一,在學習、解題過程中廣泛應用.把復雜問題簡單化,利用圖形一目了然,充分體現圖形的直觀性,代數推理的邏輯性.
數形結合;集合;函數;方程;向量;幾何
下面從以下幾個方面來談一下數形結合在解題中的應用:
1.數形結合思想在解決集合問題中的應用.
2.利用數形結合求函數的相關問題.
3.利用數形結合解方程有關問題.
4.利用數形結合解決向量問題.
5.利用數形結合研究平面幾何問題.
一、數形結合思想在解決集合問題中的應用
例1 某班共30人,其中15人喜歡數學,10人喜歡英語,8人對這兩門都不喜愛,則喜歡數學但不喜歡英語的人是多少.

解析設兩門都喜歡的人為x,畫出韋恩圖(如圖)得到方程15-x+x+10-x+8=30?x=3,
∴喜歡數學但不喜歡英語的人數為15-3=12.
析利用韋恩圖法解決集合之
間的關系問題.能直觀地解答有關集合之間的關系的問題.
二、利用數形結合求函數的相關問題
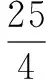


點評用數形結合的方法,先畫出函數的圖象,由圖象可直觀得解.
三、利用數形結合解方程有關問題
例3 已知函數f(x)滿足f(x+8)=f(x),且在區間[0,2]上是增函數,定義域為R且為奇函數,若方程f(x)=m(mgt;0)在區間[-8,8]上有四個不同的跟x1,x2,x3,x4,則x1+x2+x3+x4=____.

解析∵f(x+8)=f(x),∴T=8.又∵f(x)在區[0,2]上是增函數,且為奇函數,∴f(x)在[-2,0]上也是增函數,如圖,則f(x)=m(mgt;0)在[-8,8]上有四個根x1,x2,x3,x4,設x1lt;x2lt;x3lt;x4,x1+x2=-12,x3+x4=4,∴x1+x2+x3+x4=-12+4=-8.
點評關于根的分布問題,均可引入函數,利用函數圖象解決方程根的分布、不等式問題,使問題得以巧妙解決.
四、利用數形結合解決向量問題

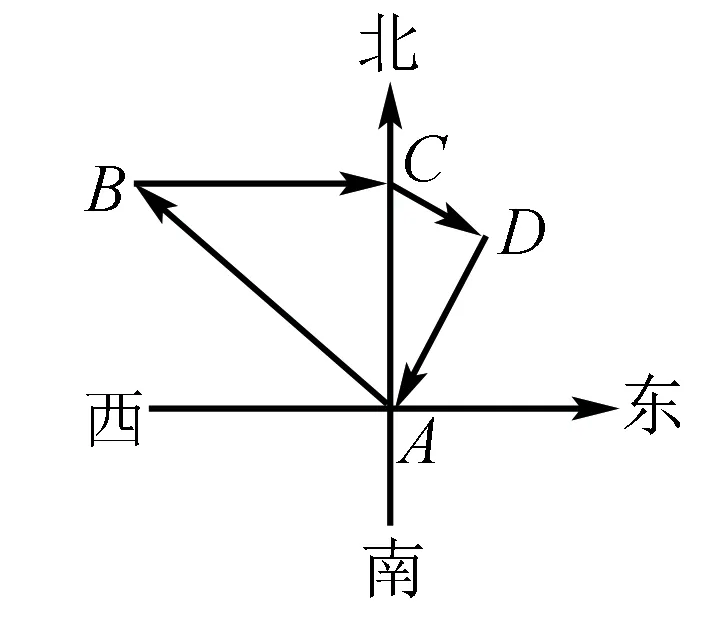

點評借助圖形解決平面向量的方向問題一目了然.
使用數形結合解題時對有些問題,只是從代數的角度去分析需要分類討論,計算會較繁,所以應想辦法從圖形的角度去分析問題的條件和結論,使復雜的關系變得簡單,思路頓開.數形結合不應僅作為一種解題方法,而
應作為一種重要的數學思想,它是將知識轉化為能力的工具.在教學中應多用多媒體這樣更有利于于突破教學難點,有利于顯示復雜的關系,使學生更容易理解題意,激發學生的學習興趣,使學生喜歡數學. 雖然數形結合思想在一些解題過程使問題簡單化但是注意不是所有問題都可以用圖形解決,圖形只是解題過程中起到輔助作用不能用它證明或者代替嚴格的邏輯代數運算.還有切記利用數形結合解題時這個“形”一定要盡量準確,這樣才能保證能準確地運算分析.
[1]張小軍. 例談高中數學數形結合解題法教學的有效策略[J]. 高中數理化,2013(20).
[2]李花花. 高中數學教學中運用數形結合提高解題能力的研究[D]. 天津師范大學,2008.
[3]李紅梅. 例談數形結合在高中數學中的應用[J]. 新課程研究(基礎教育),2010(05).
[責任編輯:楊惠民]
G632
A
1008-0333(2017)25-0006-02
2017-07-01
王芳(1982.8-),女,大學本科,中一職稱,從事高中數學教學.

