向量世界的“厚積薄發(fā)”
吳 菲
(江蘇省南京市高淳區(qū)湖濱高級中學(xué),江蘇 南京 211316)
向量世界的“厚積薄發(fā)”
吳 菲
(江蘇省南京市高淳區(qū)湖濱高級中學(xué),江蘇 南京 211316)
平面向量作為高考必考的內(nèi)容,其應(yīng)用性往往是學(xué)生薄弱的一塊,本文就此進(jìn)行討論,希望引起共鳴.
向量;不等式;立體幾何

圖1
平面向量作為高中數(shù)學(xué)中重要的一章,歷年來備受各種考試的重視,尤其是在高考中,更是雷打不動的出現(xiàn).向量這一章以其靈活多變的題型和方法,對于學(xué)生而言,也是一個(gè)很大的重點(diǎn)和難點(diǎn).向量作為代數(shù)和幾何的綜合體,向量問題本身的解決多半就有代數(shù)和幾何的方法,尤其突出一點(diǎn)的是,向量可以作為一種工具,解決數(shù)學(xué)中很多其他的問題.本文就來談一下關(guān)于向量在數(shù)學(xué)其他問題當(dāng)中的應(yīng)用,讓我們來體會向量這個(gè)工具的優(yōu)越性.
例1 如圖1所示,無彈性的細(xì)繩OA,OB的一端分別固定在A,B處,同質(zhì)量的細(xì)繩OC下端系著一個(gè)稱盤,且使得OB⊥OC,試分析OA,OB,OC三根繩子受力的大小,判斷哪根繩子受力最大.
解析本道題是高中物理當(dāng)中的一道力的問題,其實(shí)在高中物理中,我們也提到了向量,但是跟高中數(shù)學(xué)當(dāng)中有所不同的是, 物理當(dāng)中沒有數(shù)學(xué)中所表述的具體和集中,例如這道題,對于三根繩子的受力大小,其實(shí)就是我們所說的向量的模長.設(shè)繩子OA受力為a,OB受力為b,OC受力為c,由三力平衡可得a+b+c=0,由于b和c的夾角為90°,所以a=-b-c,兩邊取其模,可得|a|=|-b-c| ,由向量中|a|2=a·a,|a|2=|-b-c|2=(-b-c)2=b2+c2+2b·c=|b|2+|c|2,所以我們能看出a的模長最大,故而繩子OA所受的力最大,將這道題利用向量來解決,其實(shí)就是模長的問題,所以極大地簡化了問題.




向量不僅在代數(shù)中有諸多應(yīng)用,在立體幾何問題中,點(diǎn)到點(diǎn),點(diǎn)到線,點(diǎn)到面的距離,線面所成角,面面所成角,還有線面,面面的位置關(guān)系這些題型當(dāng)中都有很大的優(yōu)越性,使用向量的方法求解立體幾何問題,其實(shí)就是一個(gè)將圖形量化的過程,過程單一且直觀,學(xué)生易掌握,以下舉例說明.

(1)在平面PAB內(nèi)找一點(diǎn)M,使得直線CM平面PBE,并說明理由;
(2)若二面角P-CD-A的大小為 ,求直線PA與平面PCE所成角的正弦值.

由已知,CD⊥PA,CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD.于是CD⊥PD,
從而∠PDA是二面角P-CD-A的平面角,所以∠PDA=90°.
由PA⊥AB,可得PA⊥平面ABCD
設(shè)BC=1,則在Rt△PAD中,PA=AD=2


設(shè)平面PCE的法向量為n=(x,y,z),


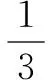
新課程加強(qiáng)了平面向量的應(yīng)用,教材中也設(shè)計(jì)了不少用向量方法研究平面圖形性質(zhì)的問題,隨著高考的改革,向量在中學(xué)數(shù)學(xué)中的地位應(yīng)該越來越高,其靈活多變的形式,以及以上我們提到的向量的應(yīng)用必將成為考試的熱點(diǎn),我期待此文投石問路,期待大家能利用向量解決越來越多的問題.
[1]中華人民共和國教育部.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(實(shí)驗(yàn))[S].北京:人民教育出版社,2003.
[2]劉玉斌.向量在幾何中的應(yīng)用[J].科技視野,2013(23):133.
[責(zé)任編輯:楊惠民]
G632
A
1008-0333(2017)25-0012-02
2017-07-01
吳菲(1983.3-),女,安徽人,現(xiàn)任南京市高淳區(qū)湖濱高級中學(xué)教師,從事高中數(shù)學(xué)教學(xué)研究.

