淺談估算法在物理問題中的應用
王紅林
(江蘇省口岸中學,江蘇 泰州 225321)
淺談估算法在物理問題中的應用
王紅林
(江蘇省口岸中學,江蘇 泰州 225321)
應用估算法解決物理問題是對學生物理過程建模、挖掘隱含條件、尋找恰當關系、進行近似計算多方面能力的綜合考查,引導學生加強物理過程的分析,深刻理解物理本質,抓住主要因素,借助有關物理概念、規律進行邏輯推理,注重日常數據的積累,提高近似計算能力是解決估算問題的關鍵.
估算問題;近似計算方法;物理
估算法不僅是一種近似計算方法,也是處理物理實際問題的重要方法.多年來估算問題在高考試卷中屢見不鮮,是學生的主要失分點之一.由于估算問題涉及實際物理情景,條件隱蔽,應用性強,對學生多方面能力要求頗高,常使學生無能為力,因此在平時的教學中有意識對學生加強估算方法的訓練,培養建模和近似計算的能力就顯得很有必要.下面通過幾個具體估算問題的分析,就如何有效進行估算問題教學談談幾點體會.
1.建立恰當的物理模型
估算問題涉及的實際情景可能熟悉,但物理過程和所對應的物理模型往往比較隱蔽,弄清物理過程,根據實際情況抓住主要的本質要素,建立便于計算的簡化模型成為突破估算問題的關鍵.
例1 研究表明,人步行時重心升降的幅度約為腳跨一步距離的0.1倍.某同學在水平面上勻速步行1Km的過程中,他做的功約為( ).
A.1.6×102J B. 6×103J C.6×104J D.6×105J

2.挖掘隱含的物理條件
估算問題表述簡潔,顯含條件很少,需要深入挖掘物理過程和狀態中所隱含的條件和關系,根據模型涉及的概念和規律找到所求物理量的表達式.
例2 利用三顆位置恰當的地球同步衛星,可使地球赤道上任意兩點間保持無線電通訊.目前地球同步衛星的軌道半徑為地球半徑的6.6倍,假設地球的自轉周期變小,若仍然僅用三顆同步衛星來實現上述目的,則地球自轉周期的最小值約為( ).
A.1h B.4h C.8h D.16h

圖1
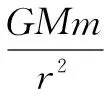
3.進行合理的數值計算
估算的目的之一是獲得數量級的認識,題中給出的數據條件較少,需要根據平時對一些常識性數據或數量級的積累和物理常量的記憶,在保留1—2位有效數字的前提下進行合理的簡化計算即可.

圖2
例3 竹蜻蜓是我國古代發明的一種兒童玩具,上世紀三十年代,人們根據竹蜻蜓原理設計了直升機的螺旋槳.如圖2所示,一小孩搓動質量為20g的竹蜻蜓,松開后竹蜻蜓能上升到二層樓房頂高處.在搓動過程中手對竹蜻蜓做的功可能是( ).
A.0.2J B.0.6J C.1.0J D.2.5J
解析竹蜻蜓上升過程中克服重力和空氣阻力做功,把手搓動竹蜻蜓獲得的動能轉化為重力勢能和內能,二樓房頂高約8m,到達該處的重力勢能約為mgh=0.02×10×8J=1.6J.則手對竹蜻蜓做的功應大于1.6J.故D正確.
[1]呂愚.例析物理估算題的求解方法[J].甘肅教育,2013(14):91—91.
[2]張港華.淺談中學物理教學中的估算問題[J].新課程學習:學術教育,2011(2).
[責任編輯:閆久毅]
G632
A
1008-0333(2017)25-0070-01
2017-07-01
王紅林(1969.1.8-),男,漢,江蘇泰州,中學高級教師,學士.

